文章编号: 1004-0609(2005)03-0429-06

金属粉末注射成形仿真分析的喂料粘度模型参数  

蒋炳炎^{1, 2}, 王 麟², 谢 磊², 黄伯云¹

(1. 中南大学 粉末冶金国家重点实验室, 长沙 410083;

2. 中南大学 机电工程学院, 长沙 410083)

摘 要: 针对喂料粘度模型参数求解和现有模流分析软件无拟合功能的问题, 引入Cross-WLF七参数模型对MIM中非牛顿流体流动过程进行了研究, 提出了自适应快速遗传算法拟合该模型参数, 开发了粘度模型参数拟合求解器, 得到了W-Ni-Fe高密度粉末喂料和316L 不锈钢喂料粘度模型的7 个参数, 拟合结果的复合相关系数分别达到0.998489和0.998200。 研究结果为高密度类零件和不锈钢类的质量预测、 模具和工艺参数优化设计提供了必须的材料数据。

关键词: 金属粉末注射成形; 遗传算法; 参数拟合; 粘度模型 中图分类号: TP31; TF124

文献标识码: A

Viscosity model parameters fitting of feedstock in

MIM simulation and analysis

JIANG Bing-yan^{1, 2}, WANG Lin², XIE Lei², HUANG Bai-yun¹

(1. State Key Laboratory of Powder Metallurgy,

Central South University, Changsha 410083, China;

2. School of Mechanical and Electrical Engineering,

Central South University, Changsha 410083, China)

Abstract: For solution of feedstock viscosity model parameters and shortage of regress function in current molding analysis software, the flow process of Non-Newtonian feedstock fluid was firstly studied by using Cross-WLF Seven-Parameter model and a Quick Self-adaptive Genetic Algorithm was built and the viscosity model parameter fitting solver was realized. The seven parameters of Cross viscosity model of W-Ni-Fe and 316L stainless MIM feedstock were fitted, the multicorrelation coefficients (R) of fitting results are 0.998489 and 0.998200, which means its accuracy is very high. Then the necessary material data was obtained for quality forecast of mold core part made of stainless steel and heavy alloy tungsten ball, and for optimal design of mold and process parameters by this way. It establishes the foundation of material database of MIM.

Key words: metal powder injection molding; genetic algorithm; parameters fit; viscosity model

   粉末注射成形仿真必须先确定喂料的粘度模型参数。 但由于影响喂料流变性能的因素多且复杂, 其粘度参数无法直接获得, 通常是以Cross粘度模型为基础, 通过实验和拟合方法得到粘度模型参数。 粘度模型参数拟合首先需要测得不同温度和剪切速率下的粘度值, 但是由于喂料的粘度参数受其组成成分的影响极大, 即使是同种材料, 不同批次或者成分稍有不同, 流变参数值也会产生很大的变化。 如HDPE-GD-6260, 其B值为0.2374, 而HDPE-ARCO-SUPRER DYLAN7004其B值为1168.0。 因此通过实验和数据拟合的方法获得粘度模型参数值, 无论是对聚合物还是金属粉末喂料都有着重要的意义。

针对聚合物熔体, 国内诸多学者对粘度模型的参数拟合算法进行了探索, 徐全军^[1]采用改进阻尼最小二乘法及自适应快速遗传算法拟合得出了Cross-Arrhenius 模型的参数; 李宁^[2]提出应用Gauss-Newton 法拟合Cross-Arrhenius 模型的参数; 张等^[3]运用逐步线性化法解决了Cross-Arrhenius 模型求解的初值问题, 并拟合得出模型参数。

针对金属喂料熔体, Kwon等^[4]提出了基于Cross-Arrenius 模型的屈服应力粘度修正模型, 采用曲线拟合法求解模型参数; 敖等^[5]采用幂率模型作为喂料粘度模型, 对实验数据进行曲线拟合。

由此可见, 粘度模型参数拟合算法的研究对象主要面向Cross-Arrhenius 五参数模型, 研究范围主要针对聚合物注射成形领域, 而且算法研究过程中未考虑不同算法的结合与互补。 基于此, 本文作者将Cross-WLF模型引入MIM 研究, 并针对喂料粘度模型参数求解和现有模流分析软件无拟合功能的问题, 提出了自适应快速遗传算法拟合该模型参数, 为金属粉末注射成形的充模仿真分析奠定材料数据库基础。

 1 遗传算法的改进

遗传算法(Genetic Algorithm, 简称GA)的基本思想是基于Darwin进化论和Mendel的遗传学说, 即将问题的求解表示成“染色体”, 从而构成一群“染色体”, 用计算机编程时, 每一条染色体用一个二进制码串表示^[6-9], 将它们置于问题的“环境”中, 根据适者生存的原则, 从中选择出适应环境的“染色体”进行复制, 通过交换、 变异两种基因操作产生出新一代更适应环境的“染色体”群, 这样一代代不断地进化, 最后收敛到一个最适应环境的个体上, 求得问题的最优解^[10-13]。

然而, 在应用传统遗传算法求解问题的过程中发现, 运算初期解的收敛速度非常快, 但是遗传演化到一定的程度, 解的收敛变得非常缓慢, 无法满足拟合计算的需要。 针对这一不足, 本文作者从进化方法与解的取值区间选取方法, 对自适应快速遗传算法收敛速度的影响进行了研究。

1.1 进化方法的改进

传统遗传算法中, 根据父代的优劣程度选择交叉个体, 优胜的个体被选中的可能性较大, 但这并不能保证选中的一定是最优的。 当群体进化到一定程度时, 可能出现近亲过多的情况, 这时候将导致群体无法进化或者进化速度很慢。 为此提出以下遗传算法的进化方法, 以克服传统算法的不足。

第一步 尽可能选择能包括真实解在内的最小区间, 然后将解进行二进制编码, 随即产生由N个体组成的初始群体, 每个个体的染色体长度为L;

第二步 计算每个个体的适应度, 选出适应度最好的个体b₁, 如果b₁的适应度满足进化给定的阀值, 则停止进化, 输出结果;

第三步 如果群体中有A个个体(A>N/2)与b₁的适应度接近, 说明群体的近亲程度过高, 把除了b₁以外的所有其他个体进行变异, 然后转第二步;

第四步 选择适应度第二大的个体b₂, 产生一个介于1与L之间的随即数M, 然后在b₁与b₂上随机选择M个位置进行交叉;

第五步 比较交叉后产生的两个子代b′₁、 b′₂, 将适应度较小的个体进行变异, 变异的方法是产生介于1与L/4之间的随机数C, 随机选择C个位置(位置可以重叠), 在这些位置上对二进制数求反;

第六步 比较变异后的子代, 将适应度较高的个体取代父代中适应度最差的个体, 转第一步执行。

1.2 取值区间选取方法的改进

在使用遗传算法拟合实验数据进行再计算的过程中发现, 虽然不同计算阶段解的收敛速度差别很大, 但收敛的趋势总向真值逼近。 例如, 在对CROSS-WLF粘度模型参数拟合时, 其中一参数τ^*在进化初期, 解迅速向真值收敛(τ^*的真值为42592.2), 而到了一定程度后(约500次左右), 虽然收敛速度显著变慢, 但总的趋势仍然向真值逼近, 如图1所示。

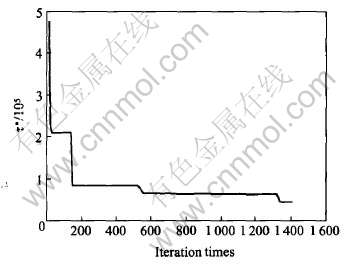
图1  进化迭代过程中τ^*解值的收敛趋势

Fig.1   Convergence trend of result for τ^* during iteration and evolution

 本文作者在研究改进GA收敛速度方法的过程中发现, 其收敛速度与解的取值范围有关, 取值范围越准确, 收敛速度越快。 因此, 基于上述原理, 提出了如下取值边界自适应的方法。

当GA经过m次迭代收敛速度趋于缓和之后, 每隔K次迭代取一次待求参数的参考值x_i, i=1, 2, …, n(n为待求参数的个数), 本文m取500, K取500。 将每次的参考值与上次所取的参考值进行比较, 根据参考值的变化来重新确定每个待求参数的取值范围。 假设每个待求参数x_i的取值范围为[g_i, h_i], 第x^k-1_i与x^k_i次参考所取的参考值分别为与, 则当x^k_i≥x^k-1_i时, 所求参数新的取值区间变为

反之, 当x^k_i〈x^k-1_i时, 所求参数新的取值区间变为

式中 C为边界收缩因子(C>0), C值越小, 则边界收缩越快, 但同时把真值排除在求解区间的可能性也越大, 经过多次实践, 推荐C取4。

对于每K次迭代, 按照式(1)与式(2)的方法进行边界收缩, 结果发现这一取值区间的选取方法有效地提高了GA法收敛的速度。

2 改进的遗传算法用于CROSS-WLF粘度模型参数拟合

2.1 Cross-WLF粘度模型

喂料熔体绝大多数是非牛顿流体, 为了定量地表示熔体的流动规律, 通过实验研究人员总结出一般条件下粉末注射成形喂料熔体的粘度模型。 采用Cross-WLF模型^[11-15], 粘度(η)可表示为

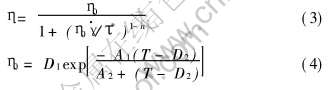
式(3)为Cross粘度模型, 式(4)为用WLF方程表示的零剪切速率时的粘度η₀。

式中 τ^*为熔体的剪切变稀特性; γ[DD(M-*2]·[DD)]为剪切速率; n为非牛顿指数; D₁为非结晶体, 即在玻璃化温度下的零剪切率粘性系数; D₂为非结晶物, 即是玻璃化转换温; A₁、 A₂为决定热膨胀系数的参数量。

对于模型中的6个参数τ^*、 n、 D₁、 D₂、 A₁、 A₂可在大量实验数据的基础上, 采用拟合求解的方法得到。

2.2 改进GA法对粘度模型参数的拟合求解法

2.2.1 确定适应度函数

根据GA原理, 首先确定适应性度函数F(b_i)。 设η′_i为b_i对应的拟合系数所对应的粘度, 则

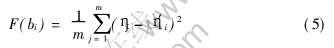
式中 b_i为第i串染色体; m为实验数据组数; η_j为第j组实验数据的粘度。 显然适应度函数值F(b_i)越小, 其适应性越好, 误差越小。

2.2.2 染色体编码

对于待拟合的6个参数, 考虑到计算的方便, 每一个参数用一个32位(4字节)的二进制编码表示, 6个参数为一串染色体, 那么每一个串长是192位(24字节), 其中0~31位表示τ^*, 32~63位表示n, 64~95位表示D1, 96~127位表示D₂, 128~159位表示A₁, 160~191位表示A₂。

以n为例, n的取值区间为[n_min, n_max]。 同时, 参数n对应的二进制编码的无符号整数值为W_n, 则二进制编码与流变参数的关系为

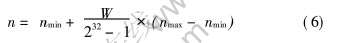
定义好适应度函数与二进制的编码方案后, 按照上述的计算步骤进行计算。

2.2.3 拟合结果精度

对于拟合的结果精度, 可用复合相关系数R来判定

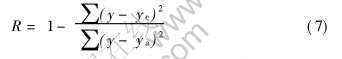
式中 y为实验值; y_c为由拟合出的参数回代求得的值; y_a为平均值。 R值越大, 精度越高(R〈1)。

2.2.3 Cross-WLF粘度模型参数拟合求解器

针对喂料粘度模型参数求解和现有模流分析软件MPI无拟合功能的问题, 在上述自适应快速遗传算法机理的基础上, 采用Visual C⁺⁺ 与 Delphi程序开发平台编制了粘度模型参数拟合求解器, 其可独立运行计算也可作为模流分析软件的一个模块为注射成形充模仿真提供必须的材料流变数据, 如图2所示, 图中间输入实验测定数据, 左侧为6个参数的取值区间的初始设定和算法控制, 右侧为根据左侧算法得到的结果。

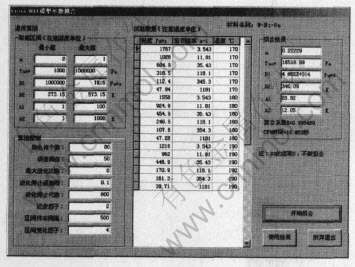
图2  Corss-WLF粘度模型参数拟合器

Fig.2   Fitting solver of Cross-WLF viscosity model parameters

3 Cross-WLF粘度模型在金属粉末注射成形仿真分析中的应用

3.1 W-Ni-Fe喂料粘度模型参数拟合

以高密度粉末喂料W-Ni-Fe为例, 将其对应的Cross-WLF粘度模型参数进行拟合。 喂料由45%(体积分数)的W-Ni-Fi粉末与55%(体积分数)的粘结剂组成, 在170、 180、 190℃下对喂料的剪切速率与粘度进行了测量, 测量结果列于表1^{[16, 17]}。

对需要拟合的参数,其取值区间为n取0~1; τ^*取1000~1000000Pa; D₁取1.0×10⁶ ~1.0×10¹⁵Pa·s; D₂取273.15~573.15K; A₁取1~100; A₂取1~1000K。

将表1中的实验数据与待拟合参数的取值区间输入粘度模型参数拟合器进行求解, 可得: n=0.22229, τ^*=16518.99Pa, D₁=4.865×10¹⁴Pa·s, D₂=340.09K, A₁=28.82, A₂=12.05K。 利用式(7)求得复合相关系数R=0.998489, 说明拟合结果相当精确, 可以作为粉末注射成形仿真分析的粘度模型参数。 将拟合结果代入Cross-WLF粘度模型, 得到160~200℃下剪切速率与粘度的关系, 如图3所示。

表1   不同温度时各种剪切速率下W-Ni-Fe喂料的粘度值

Table 1   Viscosity of W-Ni-Fe feedstock at different temperatures and shear rates (Pa·s)

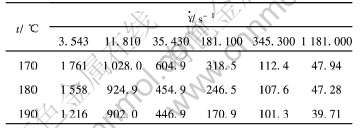
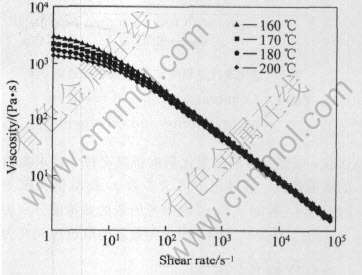
图3  W-Ni-Fe喂料粘度与剪切速率的关系

Fig.3   Relationship between viscosity and shear rate for W-Ni-Fe feedstock

3.2 316L不锈钢喂料粘度模型参数拟合

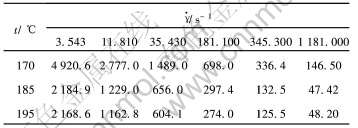
同理, 对316L不锈钢粉末喂料Cross-WLF粘度模型进行参数拟合。 采用316L不锈钢粉末(15μm, 球形), 采用聚缩醛基粘结剂, 粉末体积装载量为(体积分数)61%~63%, 在170、 185、 195℃下对喂料的剪切速率与粘度进行了测量, 测量结果列于表2^[18]。

表2   不同温度时各种剪切速率下316L不锈钢喂料的粘度值

Table 2   Viscosity of 316L Stainless feedstock at different temperatures and shear rates (Pa·s)

拟合得到粘度模型参数值为: τ^*=6235.8Pa, n=0.4032, D₁=4.589×10¹⁴Pa·s, D₂=426.9K, A₁=26.45, A₂=2.19K, 将拟合结果代入Cross-WLF粘度模型, 得到170~200℃下剪切速率与粘度的关系, 如图4所示, 其复合相关系数R=0.998200, 拟合结果也相当精确。

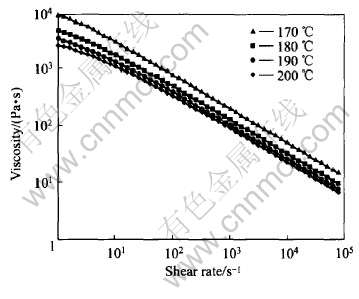
图4  316L不锈钢喂料粘度与剪切速率的关系

Fig.4   Relationships between viscosity and shear rate for 316L stainless feedstock

 4 结论

研究了金属粉末注射成形仿真过程中的粘度模型参数的求解问题, 并从充模流动过程仿真实际出发, 根据实验测得数据, 采用自适应快速遗传算法拟合了非牛顿流体粘度模型参数, 为粉末注射成形流动过程的仿真分析提供了不同温度和压力条件下的粘度模型参数。

1) 在MIM 喂料流变方程研究方面, 引入Cross-WLF 七参数模型对MIM中非牛顿流体流动过程进行研究, 并提出自适应快速遗传算法拟合该模型参数。

2) 在传统遗传算法基础上, 改进解的取值区间选取方法和进化算法, 加快解的收敛速度, 提出自适应快速遗传算法, 并用于金属粉末喂料的Cross-WLF模型七参数拟合, 有效地解决了由于模型参数较多、 形式复杂而一般方法难以拟合的问题。

3) 在提出的自适应快速遗传算法的基础上, 采用Visual C⁺⁺ 与 Delphi程序开发平台编制了Cross-WLF粘度模型参数拟合求解器, 可以方便地进行粉末喂料粘度模型参数的拟合求解。

4) 以W-Ni-Fe和316L不锈钢粉末喂料为例, 对其Cross-WLF模型的流变参数进行了拟合, 得到了金属粉末注射成形喂料流动仿真所需Cross-WLF 粘度模型的7个参数值, 具有相当高的精度, 解决了两类材料零件的注射成形充模仿真过程中的粘度数据问题。

REFERENCES

[1]徐全军. 注塑材料流变参数拟合[J]. 塑料科技, 1993(3): 19-24.

XU Quan-jun. Rheology parameters regression of materials for injection molding[J]. Plastics Technology, 1993(3): 19-24.

[2]李宁. 基于G-N法的高聚物粘度模型参数拟合[J]. 郑州工业大学学报, 2000, 21(4): 55-57.

Li Ning. G-N fitting method of polymer viscosity mold[J]. Journal of Zhengzhou University of Technology, 2000, 21(4): 55-57.

[3]张杰, 王克立, 王鹏驹, 等. 塑料熔体充模流动粘性模型的数值求解[J]. 中国塑料, 1998, 12(4): 101-105.

ZHANG Jie, WANG Ke-li, WANG Peng-ju, et al. A Numerical analysis of viscosity model for melt in injection filling molds[J]. China Plastics, 1998, 12(4): 101-105.

[4]Kwon T H, Ahn S Y. Slip characterization of powder/binder mixtures and its significance in filling process analysis of powder injection molding[J]. Powder Technology, 1995(1): 45-49.

[5]敖晖. 粉末注射成形充模流动计算机模拟[D]. 长沙: 中南大学, 2002.

AO Hui. Computer Simulation of MIM Filling Process[D]. Changsha: Central South University, 2002.

[6]Gábor R, Anikó E. Genetic algorithms in computer aided design[J]. Computer-Aided Design, 2003, 35(8): 709-726.

[7]Lee C W, Shin Y C. Construction of fuzzy systems using least-squares method and genetic algorithm[J]. Fuzzy Sets and Systems, 2003, 137(3): 297-323.

[8]Kim B Y, Nam G J, Ryu H S, et al. Optimization of filling process in RTM using genetic algorithm[J]. Korea-Australia Rheology Journal, 2000, 12(1): 83-92.

[9]Gautam G, Chaudhuri B B. A novel genetic algorithm for automatic clustering[J]. Pattern Recognition Letters, 2004, 25(2): 173-187.

[10]林国扶, 李冠英. 一个用遗传算法求解的实例[J]. 华南师范大学学报(自然科学版), 1994(3): 38-42.

LIN Guo-fu, LI Guan-ying. An example solved by genetic algorithms[J]. Journal of South China Normal University(Natural Science Edition), 1994(3): 38-42.

[11]张晓绩, 戴冠中, 徐乃平. 一种新的优化搜索算法: 遗传算法[J]. 控制理论与应用, 1995, 12(3): 265-274.

ZHANG Xiao-ji, DAI Guan-zhong, XU Nai-ping. Genetic algorithms: a new optimization and algorithm[J]. Control Theory and Application, 1995, 12(3): 265-274.

[12]恽为民, 席裕庚. 遗传算法的运行机理分析[J]. 控制理论与应用, 1996, 13(3): 297-305.

YUN Wei-min, XI Yu-geng. The analysis on running mechanism of genetic algorithm[J]. Control Theory and Application, 1996, 13(3): 297-305.

[13]徐全军, 李德群. 基因遗传改进算法用于注塑材料流变参数拟合[J]. 机械与电子, 1994(1): 23-24.

XU Quan-jun, LI De-qun. Application of improved genetic algorithm in rheology parameters regression of materials for injection molding[J]. Mechanical and Electronical,1994(1): 23-24.

[14]张杰. 注塑级塑料粘性模型研究[J]. 塑料工业, 1995(3): 39-41.

ZHANG Jie. Study on viscosity model of materials for injection molding[J]. Plastics Technology, 1995(3): 39-41.

[15]许静静. 金属粉末注射成形工艺参数及浇口尺寸对流动性能的影响[D]. 长沙: 中南大学, 2003.

XU Jing-jing. Effects of the Gate Dimension and Processing Parameters on Molding Capability in Metal Injection Molding [D]. Changsha: Central South University, 2003.

[16]李益民, 曲选辉, 黄伯云, 等. 金属注射成形喂料的流动行为及粘度参数的测定[J]. 稀有金属材料与工程, 1996, 26(1): 41-43.

LI Yi-min, QU Xuan-hui, HUANG Bai-yun, et al. The flow behavior and viscosity determination of the feedstock of metal injection molding[J]. Rare Metal Materials and Engineering, 1996, 26(1): 41-43.

[17]李益民, 曲选辉, 黄伯云. 金属注射成形喂料的流变学性能评价[J]. 材料工程, 1999(7): 34-36.

LI Yi-min, QU Xuan-hui, HUANG Bai-yun. Evaluation of rheological properties of metal injection molding feedstocks[J]. Materials Engineering, 1999(7): 34-36.

[18]Bilovol V V, Kowalski L, Duszczyk J, et al. Characterisation of 316L PIM feedstock for purpose of simulation of PIM[J]. Powder Metallurgy, 2003, 46(3): 236-240.

(编辑陈爱华)

基金项目: 国家重点基础研究发展规划资助项目(G2000067200)

收稿日期: 2004-05-25; 修订日期: 2004-12-20

作者简介: 蒋炳炎 (1963-), 男, 教授.

通讯作者: 蒋炳炎, 教授; 电话: 0731-8830758; 传真: 0731-8710201; E-mail: jby@mail.csu.edu.cn