
Elastic-plastic properties of thin film on elastic-plastic substrates characterized by nanoindentation test
JIANG Li-mei(蒋丽梅)1, 2, ZHOU Yi-chun(周益春)2, HUANG Yong-li(黄勇力)2
1. College of Packaging and Material Engineering, Hunan University of Technology, Zhuzhou 412007, China;
2. Key Laboratory of Low Dimensional Materials and Application Technology of Ministry of Education,
Xiangtan University, Xiangtan 411105, China
Received 9 October 2009; accepted 31 January 2010
Abstract: To characterize the elastic-plastic properties of thin film materials on elastic-plastic substrates, a simple theory model was proposed, which included three steps: dimensionless analysis, finite element modeling and data fitting. The dimensionless analysis was applied to deriving two preliminary nondimensional relationships of the material properties, and finite element modeling and data fitting were carried out to establish their explicit forms. Numerical indentation tests were carried out to examine the effectiveness of the proposed model and the good agreement shows that the proposed theory model can be applied in practice.
Key words: elastic-plastic thin film; nanoindentation test; dimensionless analysis; finite element analysis
1 Introduction
Thin films are ubiquitous in modern technology, from integrated circuits to thermal barrier coatings, due to its high performance, density and smaller overall size. However, in practical applications, there are many difficulties. For instance, thin films often experience very high stresses during service which can lead to distortion of the device, deformation, fracture or decohesion of the film and degradation of the film due to enhanced diffusion or corrosion; and all these could eventually affect the functionality of the thin film/substrate layered system. Furthermore, the microstructural aspects of materials in the form of thin films can be quite different from those of the same materials in bulk form which can lead to unexpected mechanical behavior[1-2]. Therefore, in order to understand, predict and improve the reliability of devices containing thin films, it is necessary to characterize the mechanical properties of thin films.
Nanoindentation test has been successfully used to evaluate the mechanical properties of thin films due to its capability of deforming materials on a micro or nano-scale and measuring their elastic-plastic properties in situ[3-4]. However, most previous studies about depth-sensing nanoindentation technique demonstrate that, to extract the mechanical properties of the coatings or films from the indentation test, we should limit the indentation depth less than 10%–20% of the film thickness in order to avoid the influence of the substrate[5-6]. As we know, during nanoindentation experiments, especially when the indentation depth is 100-1 000 nm, size-scale-dependent indentation effects is inevitable[7-9]. Thus, for material system with very thin film, it becomes extremely difficult to obtain the intrinsic mechanical properties of the film by the indentation test when the indentation depth is too shallow. The indentation depth has to be larger than 10%-20% of the film thickness in this situation and the effects of elastic-plastic deformation of the substrate should be considered.
Recently, as for an elastic-plastic film coated on an elastic substrate system, MA et al[10] and ZHAO et al[11] proposed the techniques which can extract the film elastic-plastic properties considering the influence of the elastic substrate from one conical indentation test using the finite element method (FEM). Whereafter, as for an elastic-plastic film coated on an elastic-plastic substrate system, based on the work of MA et al[10] and ZHAO et al[11], LIAO et al[12] proposed a technique which also considered the substrate effects to measure the elastic-plastic properties of thin film materials. In all these studies, dimensional analysis was carried out to derive three preliminary nondimensional relationships among total work, reversal work, residual penetration of indentation test and elastic-plastic properties of thin film, respectively. In order to obtain the values of total work and reversal work, it first needs to integrate the loading and unloading curves. Then, by finite element and data fitting, explicit forms of these three nondimensional relationships were established. Because these techniques need integrate the loading and unloading curves and solve three equations, and they are a little complicated for engineering applications.
In this work, a new theory model was proposed to measure the elastic-plastic properties of thin film materials on elastic-plastic substrates directly from force—displacement curve of nanoindentation test. Like the method proposed by LIAO et al[12], this theory model also considers the substrate effects and includes three steps: dimensional analysis, finite element modeling and data fitting. But compared with those proposed by previous studies, it needn’t integrate the loading and unloading curves, and just concludes two nondimensional equations. So, this study provides a simple framework to extract elastic–plastic properties of elastic–plastic film by considering the influence of the elastic–plastic substrate from one indentation test that is widely applicable.
2 Theory model
Considering a rigid, conical indenter indenting into an elastic–plastic film coated on an elastic–plastic substrate (see Fig.1), both the film and substrate materials can be characterized by a power law relation defined as
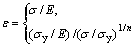

 (1)
(1)
where σy is the initial yield stress n is the power hardening exponent; and E and v are elastic modulus and Poisson ratio, respectively. The tensile behavior is generalized to multiaxial stress states by assuming isotropic hardening and using the von Mises yield surface. For thin film the parameters are denoted as σyf, nf, vf and Ef, while for substrate they are denoted as σys, ns, vs and Es. A typical loading—unloading curve is given in Fig.2, where Pm, hm and hr are the maximum indentation load, maximum indentation depth and residual penetration, respectively.

Fig.1 Schematic of normal indentation on film/substrate system
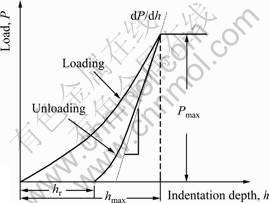
Fig.2 Typical P—h response of elastic-plastic material to nanoindentation test
Our purpose is to measure the elastic-plastic properties of thin film materials. In other words, σyf, nf, vf and Ef are the parameters that we don’t know and should be obtained in the present work. Previous studies demonstrated that the Poisson ratio v is not an important factor in the indentation experiment, and for most engineering materials v≈0.3[13-15]. In addition, because the indentation is not completely rigid, we defined a reduced elastic modulus[16], that is
 (2)
(2)
where Er is the reduced elastic modulus, Ei and vi are the elastic modulus and Poisson ratio of the indenter[16]. Er and film stiffness S have the following relationship:
 (3)
(3)
It also can be rewritten as
 (4)
(4)
where A is the contact area. Since the value of S can be calculated from the unloading curve as shown in Fig.2, Er can be easily established by Eq.(4). Once Er is known, the elastic modulus of the film Ef can be obtained with Eq.(2). Hence, there are only two material parameters ( i.e. σyf and nf) that we cannot establish indirectly from the indentation test.
In order to extract the left two parameters from the force—displacement curve of nanoindentation test, a theory model was developed.
2.1 Dimensional analysis
It is considered that each type of material has respective force—displacement curve. The following power function is adopted to fit the loading curve as shown in Fig.1.
 (5)
(5)
Dimensional analysis reveals that the maximum indentation load Pm and index x should be a function of all the independent parameters (Ef, σyf, nf, Es, σys, ns, tf, hm). Here, hf is the thickness of films. Therefore, we have
Pm=φ(σyf, nf, Ef, σys, ns, Es, hm, hf) (6)
x=φ(σyf, nf, Ef, σys, ns, Es, hm, hf) (7)
By applying the Buckingham-П theorem and choosing the dimensionless quantities that unknown parameters are normalized by known quantities, the following dimensionless forms can be obtained:
 (8)
(8)
 (9)
(9)
In order to reduce the number of parameters of Eqs.(8) and (9), hm/tf is assumed to be a constant value of 1/2. Moreover, because substrate properties σys/Es and ns in this work are considered to be known, Eqs.(8) and (9) can be simplified as
 (10)
(10)
 (11)
(11)
2.2 Finite element modelling
The FEM simulations were carried out using the commercial code ABAQUS [17] on Dell workstations. Due to the fact that the conical indenter was assumed to be axisymmetric, Fig.3 shows the mesh design for axisymmetric calculations. The semi-infinite film/substrate system of the indented solid is modeled using 9900 four-noded, bilinear axisymmetric quadrilateral elements, where a refine mesh near the contact region and a gradually coarser mesh further from the contact region have been designed to ensure numerical accuracy. The mesh was well-tested for convergence and was determined to be insensitive to far-field boundary conditions. A rigid conical surface with half apex angle of 70.3 ° was used to model the widely used Berkovich indenter. In this study, the rigid indenter is assumed to have a perfectly sharp tip. Coulomb’s friction law is used between contact surfaces with a friction coefficient of 0.1 and the friction is a minor factor in indentation[4, 18].
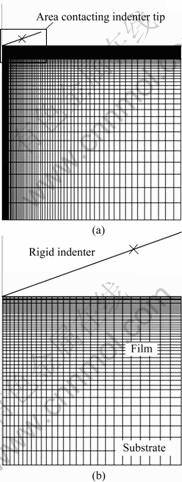
Fig.3 Finite element mesh of axisymmetric indentation: (a) Overall mesh design for conical indentation calculation; (b) Detailed illustration of area that directly contacting indenter tip
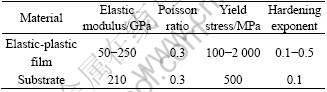
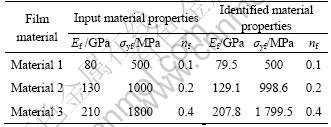
Both film and substrate are assumed to be isotropic. Generally, the initial yield and elastic modulus for metal or alloy are 0.03-1.1 GPa and 40-210 GPa respectively, while nf typically varies between 0 and 0.5. Therefore, large deformation finite element computations are carried out for combinations of elastic-plastic properties that encompass the wide range of film material parameters. The input material properties of film and substrate are listed in Table 1.
Table 1 Input material properties for finite element modeling
3 Results and discussion
3.1 Dimensionless functions
With the finite element model, large amounts of calculations are performed to study the effects of each dimensionless parameters on the right of Eqs.(10) and (11) on the indentation load Pm and index x. Lots of data are obtained at the same time. Finally, Eqs.(12) and (13) can be established by fitting the finite element simulation results:

 (12)
(12)
where the coefficients A, B, C, D, E, A1, B1, C1 and D1 are functions of nf and
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

 (13)
(13)
where the coefficients A2, B2, C2, D2, A3, B3, C3, D3, E3 also are functions of nf and
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Once the explicit form of the dimensionless is established, it is easy to identify the film material parameters Ef, σyf and nf. The detailed steps are as follows: 1) an experimental or numerical indentation test can be performed to obtain the P—h curve; 2) according to Eqs.(2)-(4), the elastic modulus of film Ef can be measured; 3) by fitting the P—h curve, the indentation load Pm and index x can be determined; 4) by substituting indentation load Pm and index x to Eqs.(12) and (13) and solving these two equations, the elastic-plastic properties of the film (σyf and nf) can be characterized.
3.2 General numerical examination of theory model
Numerical indentation tests are performed to examine the effectiveness of the theory model. The elastic-plastic properties of the substrate (Es, σys, ns) are given as: Es?210 GPa, σys?500 MPa and ns?0.1, and three different film material combinations (Ef, σyf, nf) |input with thickness of 2 mm coated on the substrate (i.e., material 1, material 2, material 3) are used as the input in FEM simulations, with hm?1/2tf. Numerical indentation tests are carried out on these materials, the P—h curves can be obtained, as shown in Fig.4. With the theory model, we can extract the set of film material properties (E*, σyf, nf) from the P—h curves, as shown in Fig.4. The identified material properties and those of the input material properties are listed in Table 2 to examine the effectiveness of the proposed algorithm. From Table 2, it can be seen that the identified film material properties are very close to those of the input data.
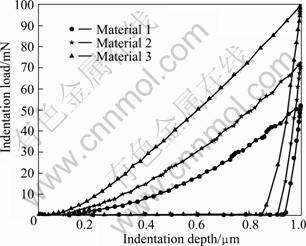
Fig.4 Indentation load—depth curves of thin films deposited on elastic-plastic substrate
Table 2 Comparisons of material properties identified by theory model proposed and input material properties
4 Conclusions
1) A theory model which effectively measures the elastic-plastic properties of thin films on elastic-plastic substrates from the force—displacement curves of the nanoindentation test was presented. It is worth noting that, compared with previous studies, this model becomes much easier for practical applications. This is because in the theory model proposed here we only need to establish two nondimensional functions, but three nondimensional functions needed to be established in previous studies.
2) The effectiveness of the theory model is verified through numerical indentation. The current analysis does not take into account of any size effects associated with plastic strain gradients. When the aforementioned assumptions are satisfied, the method in this work can be used for measuring the elastic-plastic properties of a film on an elastic-plastic substrate, which is also useful for very thin films.
References
[1] DAO M, CHOLLACOOP N, van VLIET K J, VENKATESH T A, SURESH S. Computational modeling of the forward and reverse problems in instrumented sharp indentation [J]. Acta Materialia, 2001, 49(19): 3899-3918.
[2] CHOLLACOOP N, DAO M, SURESH S. Depth-sensing instrumented indentation with dual sharp indenters [J]. Acta Materialia, 2003, 51(13): 3713-3729.
[3] DOERNER M F, NIX W D. A method for interpreting the data from depth sensing indentation instruments [J]. Journal of Material Research, 1986, 1: 601-609.
[4] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments [J]. Journal of Material Research, 1992, 7: 1564-1583.
[5] GAMONPILAS C, BUSSO E P. On the effect of substrate properties on the indentation behaviour of coated systems [J]. Materials Science and Engineering A, 2004, 380 (1/2): 52-61.
[6] PANICH N, SUN Y. Effect of penetration depth on indentation response of soft coatings on hard substrates: A finite element analysis [J]. Surface and Coatings Technology, 2004, 182 (2/3): 342-350.
[7] GERBERICH W W, NELSON J C, LILLEODDEN E T, ANDERSON P, WYROBEK J T. Indentation induced dislocation nucleation: The initial yield Point [J]. Acta Materialia, 1996, 44(9): 3585-3598.
[8] FLECK N A, HUTCHINSON J W. A phenomenological theory for strain gradient effects in plasticity [J]. Journal of the Mechanics and Physics of Solids, 1993, 41(12): 1825-1857.
[9] GAO H, HUANG Y, NIX W D, HUTCHINSON J W. Mechanism-based strain gradient plasticity—I. Theory [J]. Journal of the Mechanics and Physics of Solids, 1999, 47(6): 1239-1263.
[10] MA D J, XU KW, HE J W, LU J. Evaluation of the mechanical properties of thin metal films [J]. Surface and Coatings Technology, 1999, 116: 128-132.
[11] ZHAO M H, CHEN X, XIANG Y, VLASSK J J, LEE D, OGASAWARA N, CHIBA N, GAN Y X. Measuring elastoplastic properties of thin films on an elastic substrate using sharp indentation [J]. Acta Materialia, 2007, 55(18): 6260-6274.
[12] LIAO Y G, ZHOU Y C, HUANG Y L, JIANG L M. Measuring elastic–plastic properties of thin films on elastic—Plastic substrates by sharp indentation [J]. Mechanics of Materials, 2009, 41(3): 308-318.
[13] LUO J, LIN J. A study on the determination of plastic properties of metals by instrumented indentation using two sharp indenters [J]. International Journal of Solids and Structures, 2007, 44(18/19): 5803-5817.
[14] CHENG Y T, CHENG C M. Can stress-strain relationships be obtained from indentation curve using conical and pyramidal indenters [J]. Journal of Material Research, 1999, 14(9): 3493-3496.
[15] TUNVISUT K, O’DOWD N P, BUSSO E P. Use of scaling functions to determine mechanical properties of thin coatings from microindentation tests [J]. International Journal of Solids and Structures, 2001, 38(2): 335-351.
[16] KING R B. Elastic analysis of some punch problems for a layered medium [J]. International Journal of Solids and Structures, 1987, 23(12): 1657-1664.
[17] ABAQUS. ABAQUS 6.5 User’s Manual [M]. ABAQUS Inc, 2005.
[18] ZHAO M H, CHEN X, YAN J, KARLSSON A M. Determination of uniaxial residual stress and mechanical properties by instrumented indentation [J]. Acta Materialia, 2006, 54(10): 2823-2832.
[19] YAN J, KARLSSON A M, CHEN X. Determining plastic properties of a material with residual stress by using conical indentation [J]. International Journal of Solids and Structures, 2007, 44(11/12): 3720-3737.
(Edited by LI Xiang-qun)
Foundation item: Projects(50531060, 10525211, 10828205) supported by the National Natural Science Foundation of China; Project(10525211) supported by National Science Found for Distinguished Young Scholars of China; Project(076044) supported by the Cultivation Fund of the Key Scientific and Technical Innovation Project, Ministry of Education of China
Corresponding author: ZHOU Yi-chun; Tel: +86-731-58293586; Fax: +86-731-58292468; E-mail: zhouyc@xtu.edu.cn
DOI: 10.1016/S1003-6326(10)60653-X