CaO-FeO-Fe2O3-SiO2-Cu2O渣系作用浓度计算模型
汪金良1, 2,张传福1,童长仁2,张文海1, 3
(1. 中南大学 冶金科学与工程学院,湖南 长沙,410083;
2. 江西理工大学 材料与化学工程学院,江西 赣州,341000;
3. 中国瑞林工程技术有限公司,江西 南昌,330002)
摘 要:基于炉渣结构共存理论,建立1 523~1 733 K时的CaO-FeO-Fe2O3-SiO2-Cu2O五元渣系作用浓度计算模型,对成分(质量分数)波动范围为CaO 5%~20%,FeO 5%~50%,Cu2O 5%~25%,SiO2 5%~45%,Fe2O3 5%~70%的炉渣,计算1 523和1 573 K时的各组元作用浓度,考察碱度和温度对活度系数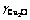 和
和 的影响,并对所得数据进行非线性回归分析。研究结果表明,理论计算值
的影响,并对所得数据进行非线性回归分析。研究结果表明,理论计算值 与文献实测值
与文献实测值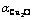 之间的相对误差小于10%,且随渣含铜增加呈直线上升的趋势一致,说明模型能较好地反映本渣系的结构本质;CaO能降低炉渣的溶铜能力,增强炉渣的溶铁能力。该模型的建立为采用铁酸钙渣系的炼铜新工艺热力学研究提供了理论依据。
之间的相对误差小于10%,且随渣含铜增加呈直线上升的趋势一致,说明模型能较好地反映本渣系的结构本质;CaO能降低炉渣的溶铜能力,增强炉渣的溶铁能力。该模型的建立为采用铁酸钙渣系的炼铜新工艺热力学研究提供了理论依据。
关键词:CaO-FeO-Fe2O3-SiO2-Cu2O渣系;共存理论;作用浓度
中图分类号:TF801 文献标识码:A 文章编号:1672-7207(2009)02-0282-06
Action concentration calculation model for slag system of CaO-FeO-Fe2O3-SiO2-Cu2O
WANG Jin-liang1, 2, ZHANG Chuan-fu1, TONG Chang-ren2, ZHANG Wen-hai1, 3
(1. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;
2. Faculty of Material and Chemistry Engineering, Jiangxi University of Science and Technology,
Ganzhou 341000, China;
3. China Nerin Engineering Co. Ltd, Nanchang 330002, China)
Abstract: In accordance to the coexistence theory of slag structure, the calculation model of action concentration for slag system of CaO-FeO-Fe2O3-SiO2-Cu2O was built up between 1 523 K and 1 733 K. With this model the action concentrations of the compounds in the slag were calculated at 1 523 K and 1 573 K, when the mass fractions of components in the slag fluctuate in the range of CaO 5%-20%, FeO 5%-50%, Cu2O 5%-25%, SiO2 5%-45%, Fe2O3 5%-70%. The influences of alkalinity and temperature on 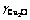 and
and  were analyzed. Then, the regression equations of the compound action concentrations were acquired by means of nonlinear regression analysis. The results show that the relative errors between the theoretical computational value
were analyzed. Then, the regression equations of the compound action concentrations were acquired by means of nonlinear regression analysis. The results show that the relative errors between the theoretical computational value  and the reported experiment measured value
and the reported experiment measured value 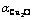 are less than 10%, and they all increase linearly with the increase of copper content in slag. It is proved that this model can reflect the structure nature of the slag system. CaO can reduce the solvency of copper but improve the solvency of iron in the slag. The establishment of this model can provide a theoretical basis for the thermodynamic research of new copper smelting technologies of adopting calcium ferrite slag.
are less than 10%, and they all increase linearly with the increase of copper content in slag. It is proved that this model can reflect the structure nature of the slag system. CaO can reduce the solvency of copper but improve the solvency of iron in the slag. The establishment of this model can provide a theoretical basis for the thermodynamic research of new copper smelting technologies of adopting calcium ferrite slag.
Key words: slag system of CaO-FeO-Fe2O3- SiO2-Cu2O; coexistence theory; action concentration
由于随着氧势的提高,吹炼或造粗铜炉渣中Fe3O4和Cu2O的含量不断增加,为了避免形成固体磁铁矿,同时最大限度地减少泡沫渣的形成,连续吹炼、三菱连续炼铜、Glogow直接闪速炼铜等现代火法炼铜技术普遍采用铁酸钙渣型[1]。
近年来,Ilyushechkin等[2-7]实验研究了铁酸钙渣的相平衡,测定了炉渣的密度、表面张力、黏度等热力学数据,绘制了液相等温线。然而,对含有高铜和高磁性氧化铁的CaO-FeO- Fe2O3-SiO2-Cu2O炉渣热力学研究较少,有关该渣系组元作用浓度及其计算模型的文献鲜有报道。
由于火法炼铜过程属高温、多相、多组分复杂体系,在一般实验室条件下其研究工作很难开展,往往借助数学和计算机技术来模拟其过程[8-10]。然而,多相反应平衡计算过程需要反复迭代计算各相各组分的作用浓度(活度)等热力学数据[11]。因此,开展CaO-FeO-Fe2O3-SiO2-Cu2O炉渣的热力学研究,建立其作用浓度计算模型,对采用铁酸钙渣系的炼铜新工艺的研究与发展具有十分重要的意义。
本文作者基于炉渣结构共存理论[12],研究建立CaO-FeO-Fe2O3-SiO2-Cu2O五元渣系作用浓度计算模型,考察碱度和温度对组元活度系数的影响,计算 1 250 ℃和1 300 ℃时的炉渣各组元作用浓度,并进行了回归分析,为采用铁酸钙渣系的炼铜新工艺热力学研究提供理论依据。
1 炉渣作用浓度计算模型
1.1 CaO-FeO-Fe2O3-SiO2-Cu2O渣系的组元
对于CaO-FeO-Fe2O3-SiO2-Cu2O五元渣系,查阅了相图[13-14]CaO-SiO2,FeO-SiO2,Cu2O-Fe2O3,FeO- Fe2O3,Cu2O-CaO-Fe2O3,CaO-FeO-Fe2O3,CaO-FeO- SiO2,根据炉渣结构的共存理论,确定了在1 250~ 1 460 ℃渣系的组元为:Cu2Fe2O4,Ca2Fe2O5,CaFe2O4,CaFe3O5,Fe3O4,CaSiO3,Ca2SiO4,Ca3SiO5,3CaO? 2SiO2,Fe2SiO4,CaFeSiO4 11种复杂化合物以及Cu2+,Fe2+,Ca2+,O2-,SiO2,Fe2O3 6种简单离子和分子。
渣中各组元之间的反应及其达到平衡时的标准吉布斯自由能 如下[15]:
如下[15]:
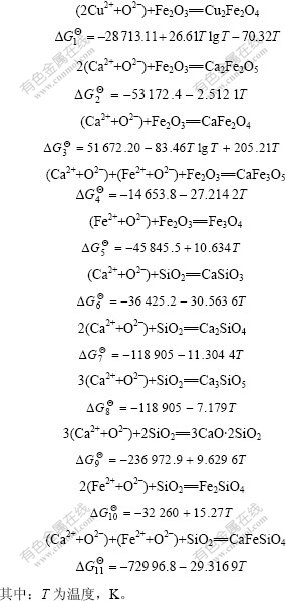
1.2 渣中各组元之间的平衡关系
假定CaO-FeO-Fe2O3-SiO2-Cu2O五元系成渣前的CaO,FeO,Cu2O,SiO2,Fe2O3的物质的量(mol)分别为m1,m2,m3,m4,m5,成渣后总物质的量为 ,各组元的作用浓度为Ni(成渣后该组元的物质的量÷
,各组元的作用浓度为Ni(成渣后该组元的物质的量÷ ),如表1所示。
),如表1所示。
表1 渣系各组元作用浓度定义
Table 1 Definition of compounds action concentration

根据质量作用定律,以下关系式成立:
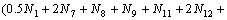
 ; (1)
; (1)
 ;(2)
;(2)
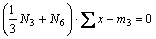 ; (3)
; (3)
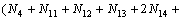
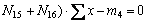 ; (4)
; (4)
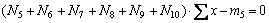 ;(5)
;(5)
 ; (6)
; (6)
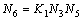 ; (7)
; (7)
 ; (8)
; (8)
 ; (9)
; (9)
 ; (10)
; (10)
 ; (11)
; (11)
 ; (12)
; (12)
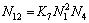 ; (13)
; (13)
 ; (14)
; (14)
 ; (15)
; (15)
 ; (16)
; (16)
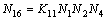 。 (17)
。 (17)
由式(1)~(17)组成的高次方程组即为求解CaO-FeO-Fe2O3-SiO2-Cu2O渣系作用浓度的计算模型,其中,K为上述各组元之间的反应平衡常数。将一定的炉渣成分代入该方程组,线性化处理后,采用高斯消去法可迭代求解出各组元的作用浓度。
2 模型验证及应用
2.1 模型验证
基于上述CaO-FeO-Fe2O3-SiO2-Cu2O渣系作用浓度模型,模拟计算温度为1 523 K时,铜在硅饱和并含CaO的铁橄榄石渣中的作用浓度,结果如图1所示,其中,铁橄榄石渣中SiO2质量分数为46%,Fe2O3为5%。
图1数据表明,理论计算的作用浓度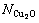 与Altman实测的活度
与Altman实测的活度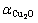 [16]较吻合。随渣含铜的增加,
[16]较吻合。随渣含铜的增加,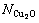 和
和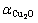 都呈直线上升,变化趋势一致,且当渣含Cu处于实践范围0%~8%时,
都呈直线上升,变化趋势一致,且当渣含Cu处于实践范围0%~8%时,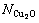 与
与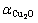 之间的相对误差小于10%,说明该作用浓度模型能较正确地反映CaO-FeO-Fe2O3-SiO2-Cu2O渣系的结构 本质。
之间的相对误差小于10%,说明该作用浓度模型能较正确地反映CaO-FeO-Fe2O3-SiO2-Cu2O渣系的结构 本质。
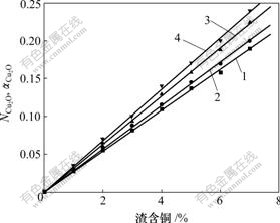
1—4% CaO,  ; 2—4% CaO,
; 2—4% CaO, 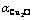 ;
;
3—9% CaO,  ; 4—9% CaO,
; 4—9% CaO, 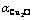
图1 计算的 与实测的
与实测的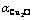 比较
比较
Fig.1 Comparison of calculated  with measured
with measured 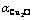
2.2 对活度系数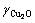 的影响
的影响
当渣中各组分质量分数为FeO 40%,Fe2O3 8%时,通过分别调整碱度B(CaO/SiO2质量比)和温度T,考察了B和T对活度系数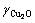 (
(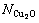 /
/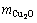 )的影响,结果如图2所示。
)的影响,结果如图2所示。
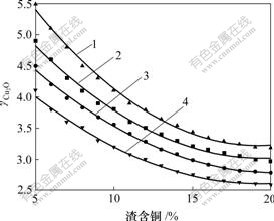
1—B=4.00, 1 523 K; 2—B=1.00, 1 523 K;
3—B=0.25, 1 523 K; 4—B=4.00, 1 573 K
图2 碱度和温度对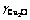 的影响
的影响
Fig.2 Influence of alkalinity and temperature on 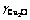
由图2可知,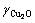 随渣含铜的升高呈先快后缓的下降趋势,随温度T的升高亦下降,但随B的增大而升高,表明温度对渣中Cu的行为有较大影响,CaO具有降低炉渣溶铜能力的作用。
随渣含铜的升高呈先快后缓的下降趋势,随温度T的升高亦下降,但随B的增大而升高,表明温度对渣中Cu的行为有较大影响,CaO具有降低炉渣溶铜能力的作用。
2.3 对活度系数γFeO的影响
当渣中各组分质量分数为Cu 8%,Fe2O3 8%时,通过分别调整碱度和温度,考察B和T对活度系数γFeO(NFeO/mFeO)的影响,结果如图3所示。
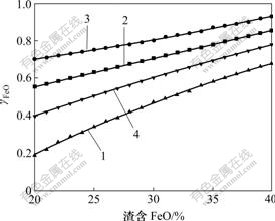
1—B=4.00, 1 523 K; 2—B=1.00, 1 523 K;
3—B=0.25, 1 523 K; 4—B=4.00, 1 573 K
图3 碱度和温度对γFeO的影响
Fig.3 Influence of alkalinity and temperature on γFeO
由图3可知,γFeO随渣含FeO的升高呈直线上升趋势,随温度的升高亦上升,但随B值的增大而下降,表明温度对渣中FeO的行为也有具有较大影响,CaO具有增强炉渣溶铁能力的作用。
3 组元作用浓度回归
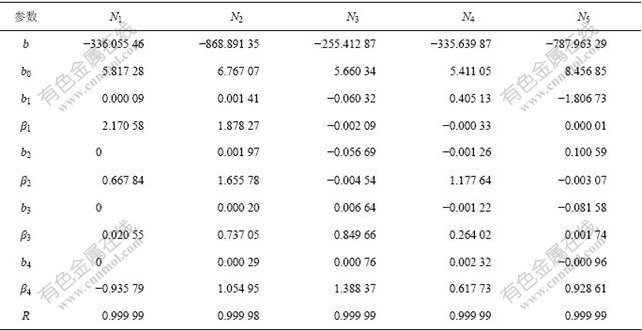
为便于应用,根据多家铜冶炼厂的实践数据,针对各组元质量分数为CaO 5%~20%,FeO 5%~50%,Cu2O 5%~25%,SiO2 5%~45%,Fe2O3 5%~70%的炉渣,利用上述作用浓度模型,分别计算了1 523 K和1 573 K时CaO-FeO-Fe2O3-SiO2-Cu2O炉渣各组元作用浓度,并进行了回归分析,得到的非线性回归方程如式(18)所示,其参数值分别列于表2和表3,其中相关系数R都接近1。
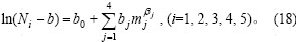
表2 1 523 K时各组元作用浓度回归方程参数值
Table 2 Parameter values of compounds action concentration regression equation at 1 523 K
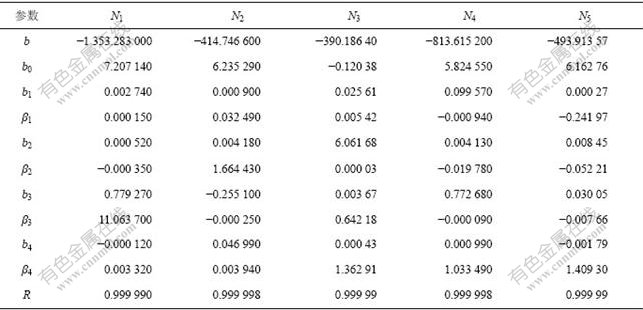
表3 1 573 K时各组元作用浓度回归方程参数值
Table 3 Parameter values of compounds action concentration regression equation at 1 573 K
4 结 论
a. 基于熔体结构共存理论,建立了1 523~1 733 K下的CaO-FeO-Fe2O3-SiO2-Cu2O五元渣系作用浓度计算模型,结果表明,理论计算值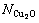 与文献实测值
与文献实测值 之间的相对误差小于10%,说明模型大体可以反映本渣系的结构本质。
之间的相对误差小于10%,说明模型大体可以反映本渣系的结构本质。
b. 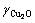 随渣含铜的升高呈先快后缓的下降趋势,随B的增大而升高,且随温度的变化明显;CaO的存在降低了炉渣的溶铜能力。
随渣含铜的升高呈先快后缓的下降趋势,随B的增大而升高,且随温度的变化明显;CaO的存在降低了炉渣的溶铜能力。
c. 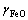 随渣含FeO的升高呈直线上升趋势,随B的增大而下降,且随温度的升高而上升;CaO具有增强炉渣溶铁能力的作用。
随渣含FeO的升高呈直线上升趋势,随B的增大而下降,且随温度的升高而上升;CaO具有增强炉渣溶铁能力的作用。
d. 对1 523 K和1 573 K时CaO-FeO-Fe2O3- SiO2-Cu2O炉渣各组元作用浓度进行了回归分析,得到了相关性良好的各组元作用浓度非线性回归方程,为采用铁酸钙渣系的炼铜新工艺热力学分析和计算机仿真奠定了基础。
参考文献:
[1] Davenport W G, King M, Schlesinger M, et al. Extractive metallurgy of copper[M]. 4th ed. New York: Pergamon Press, 2002.
[2] Ilyushechkin A, Hayes P C, Jak E. Liquidus temperatures in calcium ferrite slags in equilibrium with molten copper[J]. Metallurgical and Materials Transactions B, 2004, 35(2): 203-215.
[3] Sakai T, Ip S W,Toguri J M. Interfacial phenomena in the liquid copper-calcium ferrite slag system[J]. Metallurgical and Materials Transactions B, 1997, 28(3): 401-407.
[4] Florian K, Akira Y. Liquidus surface of FeO-Fe2O3-SiO2-CaO slag containing Al2O3, MgO, and Cu2O at intermediate oxygen partial pressures[J]. Metallurgical and Materials Transactions B, 2001, 32(4): 583-592.
[5] SangHL, SeokMM, DongJM, et al. Thermodynamic behavior of nickel in CaO-SiO2-FetO slag[J]. Metallurgical and Materials Transactions B, 2002, 33(1): 55-59.
[6] PavolV, MilanH, VladimírD. Density and surface tension of the systems CaO-FeO-Fe2O3-MgO, CaO-FeO-Fe2O3-ZnO and CaO-Fe2O3-Cu2O[J]. Central European Journal of Chemistry, 2006, 4(1): 174-193.
[7] Fahey N P, Swinbourne D R, Yan S, et al. The solubility of Cr2O3 in calcium ferrite slags at 1 573 K[J]. Metallurgical and Materials Transactions B, 2004, 35(2): 197-202.
[8] 汪金良, 卢 宏, 曾青云, 等. 基于遗传算法的铜闪速熔炼过程控制优化[J]. 中国有色金属学报, 2007, 17(1): 156-160.
WANG Jin-liang, LU Hong, ZENG Qing-yun, et al. Control optimization of copper flash smelting process based on genetic algorithms[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(1): 156-160.
[9] 喻寿益, 王吉林, 彭晓波. 基于神经网络的铜闪速熔炼过程工艺参数预测模型[J]. 中南大学学报: 自然科学版, 2007, 38(3): 523-527.
YU Shou-yi, WANG Ji-lin, PENG Xiao-bo. Prediction model of craft parameters based on neural network during the process of copper flash smelting[J]. Journal of Central South University: Science and Technology, 2007, 38(3): 523-527.
[10] 梅 炽, 姚俊峰, 胡 军, 等. 粗铜冶炼中铜锍品位的动态预测模式—AR(p)与指数平滑最优组合法[J]. 中南工业大学学报: 自然科学版, 2000, 31(1): 34-36.
MEI Chi, YAO Jun-feng, HU Jun, et al. The dynamic pre-estimating model of the grade of copper matte in the course of raw copper metallurgy: the best combined approach of autoregressive and exponential smoothing[J]. Journal of Central South University of Technology: Natural Science, 2000, 31(1): 34-36.
[11] 童长仁, 吴卫国, 周小雪. 铜闪速熔炼多相平衡数模的建立与应用[J]. 有色冶金设计与研究, 2006, 27(6): 6-9.
TONG Chang-ren, WU Wei-guo, ZHOU Xiao-xue. Establishment and application of multiphase equilibrium mathematical model for copper flash smelting process[J]. Nonferrous Metals Engineering & Research, 2006, 27(6): 6-9.
[12] ZHANG Jian. Coexistence theory of slag structure and its application to calculation of oxidizing capability of slag melts[J]. Journal of Iron and Steel Research, 2003, 10(1): 1-10.
[13] 德国钢铁工程协会. 渣图集[M]. 王 俭, 等译. 北京: 冶金工业出版社, 1989.
Verlag Stahleisen Düsseldorf. Slag atlas[M]. WANG Jian, et al, trans. Beijing: Metallurgical Industry Press, 1989.
[14] Hino M, Yazawa A. 炉渣中氧化铜的溶解平衡[C]//1995年铜国际会议论文集. 北京: 冶金工业出版社, 1998: 408-419.
Hino M, Yazawa A. The dissolve equilibrium of copper oxide in slag[C]//Proceedings of 1995 Copper International Conference. Beijing: Metallurgical Industry Press, 1998: 408-419.
[15] 梁英教, 车荫昌. 无机物热力学数据手册[M]. 沈阳: 东北大学出版社, 1993.
LIANG Ying-jiao, CHE Yin-chang. Inorganic thermodynamic data Manual[M]. Shenyang: Northeastern University Press, 1993.
[16] 朱祖泽, 贺家齐. 现代铜冶金学[M]. 北京: 科学出版社, 2003.
ZHU Zu-ze, HE Jia-qi. Modern copper metallurgy[M]. Beijing: Science Press, 2003.
收稿日期:2008-05-28;修回日期:2008-10-22
基金项目:国家重大产业技术开发项目(20051255);江西省科技攻关项目(20061B0101100);江西省自然科学基金资助项目(2007GZC0713);江西省教育厅资助项目(GJJ09241)
通信作者:汪金良(1976-),男,江西贵溪人,博士研究生,讲师,从事冶金过程数值模拟研究;电话:0797-8312270;E-mail: simwjl@163.com