J. Cent. South Univ. (2019) 26: 2464-2481

DOI: https://doi.org/10.1007/s11771-019-4187-3

Multi-objective optimization of multi-cell conical structures under dynamic loads

Pirmohammad Sadjad, Esmaeili-Marzdashti Sobhan

Department of Mechanical Engineering, University of Mohaghegh Ardabili, Ardabil 179, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: In this paper, crashworthiness performance of multi-cell conical tubes with new sectional configuration design (i.e. square, hexagonal, octagonal, decagon and circular) has been evaluated under axial and three different oblique loads. The same weight conical tubes were comparatively studied using an experimentally validated finite element model generated in LS-DYNA. Complex proportional assessment (COPRAS) method was then employed to select the most efficient tube using two conflicting criteria, namely peak collapse force (PCF) and energy absorption (EA). From the COPRAS calculations, the multi-cell conical tube with decagonal cross-section (MCDT) showed the best crashworthiness performance. Furthermore, the effects of possible number of inside ribs on the crashworthiness of the decagonal conical tubes were also evaluated, and the results displayed that the tubes performed better as the number of ribs increased. Finally, parameters (the cone angle, θ, and ratio of the internal tube size to the external one, S) of MCDT were optimized by adopting artificial neural networks (ANN) and genetic algorithm (GA) techniques. Based on the multi-objective optimization results, the optimum dimension parameters were found to be θ=7.9°, S=0.46 and θ=8°, S=0.74 from the minimum distance selection (MDS) and COPRAS methods, respectively.

Key words: crashworthiness; multi-cell conical tube; axial and oblique loads; complex proportional assessment (COPRAS); multi-objective optimization

Cite this article as: Pirmohammad Sadjad, Esmaeili-Marzdashti Sobhan. Multi-objective optimization of multi-cell conical structures under dynamic loads [J]. Journal of Central South University, 2019, 26(9): 2464-2481. DOI: https://doi.org/10.1007/s11771-019-4187-3.

1 Introduction

In order to diminish the adverse effects of vehicle crashes, energy absorbers are frequently used in the vehicle structures. Many studies on the energy absorbers have been done in the past years to increase their crashworthiness capability. Previous investigations proved that energy absorption capacity of the structures can be remarkably improved by their geometries. For example, HOSSEINI-TEHRANI and PIRMOHAMMAD [1] investigated crashworthiness of straight single-cell tubes with different cross-sections. They concluded that the octagonal single-cell tube demonstrated the best energy absorption capacity. In another task, ELMARAKBI et al [2] studied crashworthiness of the S-shaped multi-cell tubes with different cross- sections and stiffened with several ribs. The results revealed that the octagonal multi-cell tube showed better crashworthiness capability. ZOU et al [3] conducted a comparative study on the energy absorption performance of eight multi-cell polygonal tubes under axial and oblique loads. Their results showed that the multi-cell decagon tube has better energy-absorption ability compared with other tubes. HOSSEINI-TEHRANI and NIKAHD [4, 5] investigated the effect of ribs arrangements to improve energy absorption capacity. In another investigation, EYVAZIAN et al [6] studied crushing behavior of corrugated metal- composite tube experimentally under axial loading condition. MARZBANRAD et al [7] investigated crushing behavior of circular aluminum tubes with 4 and 6 blades under axial impact loading. They obtained the most important surfaces of energy absorption parameters, including the maximum displacement of the striker, the maximum axial force, the specific energy absorption and the crushing force efficiency in terms of impact velocity and tube thickness using the artificial neural network. PIRMOHAMMAD and ESMAEILI-MARZDASHTI [8] evaluated crashworthiness capability of new designed multi- cell structures called combined straight-tapered tubes to dissipate collision energy.

As such, crashworthiness of the automobile structures can be improved by using light-weight materials [9]. Aluminum alloys have been substituted to steels because of their greater ratio of strength to weight. There are also some researches that employed polymers [10-13] and metallic foams fillers [14, 15] to increase energy absorption capacity. Besides, multi-cell structures have been found to provide desirable energy absorption capability [16-21]. Compared to the foam-filled structures, the multi-cell structures showed better energy absorption capability [22].

Several studies have been carried out on the double-walled columns with straight geometry in the past years. For example, ZHANG et al [23] studied energy absorption capacity of double- walled hexagonal columns with honeycomb core under dynamic axial loading. HOSSEINI- TEHRANI and PIRMOHAMMAD [24] studied crushing behavior of concentric double-walled columns under axial and oblique loading. In this study, they introduced the best arrangement for the tubes. ZHANG et al [25] investigated crushing of foam-filled double-walled square columns under axial impact. FANG et al [26] investigated crushing behavior of foam-filled double-walled circular tubes under axial impact. DJAMALUDDIN et al [27] studied the crashworthiness capacity of three types of circular tubes, namely empty double tubes, foam-filled double tubes, and foam-filled single tubes subjected to the oblique loading. SHARIFI et al [28] investigated double-walled circular energy absorbers under quasi-static axial loading experimentally. In another study, LI et al [29] evaluated crashworthiness capacity of multi-cell thin-walled structures.

On the other hand, several works have been carried out on the tubes with conical geometry in recent years, but all of these investigations addressed crashworthiness of circular single-cell or double-cell conical tubes. For example, AHMAD and THAMBIRATNAM [30, 31] studied collapse behavior of the circular conical tubes under quasi-static and dynamic axial loading. In another study, AHMAD et al [32] evaluated dynamic energy absorption characteristics of foam-filled conical tubes. GHAMARIAN et al [33] investigated crashworthiness of circular end-capped conical tubes experimentally and numerically. HOU et al [34] optimized tapered tubes of three different configurations, namely hollow single, foam-filled single and collinear double tubes. PIRMOHAMMAD et al [35] studied crashworthiness of double-cell conical tubes. In another study, SONG et al [19] used several models to optimize crushing behavior of the foam-filled tapered columns. In addition, few investigations have been performed on the crashworthiness of tapered square tubes [36, 37]. It is found that few studies on the conical tubes with polygonal sections as well as no study on the double-walled conical tubes stiffened by several ribs have been done by researchers.

This paper focused on the crashworthiness study of the multi-cell conical tubes with new design of sectional configurations. Crashworthiness indicators including energy absorption (EA, A_e) and peak collapse force (PCF, F_pc) were obtained from the numerical simulations carried out by LS-DYNA. Besides, artificial neural network (ANN) combined with genetic algorithm (GA) was used to optimize geometry of the multi-cell conical tube.

2 Geometry description and finite element modeling

Crashworthiness of the multi-cell conical tubes has been investigated in the present work. A new sectional configuration design is proposed for the conical members. These members consist of two concentric conical tubes of identical cross-sectional shapes, including the multi-cell tubes with square (MCST), hexagonal (MCHT), octagonal (MCOT), decagonal (MCDT), and circular (MCCT), connected together by several ribs shown in Figure 1(a). The ratio of the internal tube size to the external one was set to S=0.5 for all the conical members. The perimeter of the external tube at the small end was uniformly 320 mm for all the members. The length of tubes (L) and conical angles (θ) were respectively set to 250 mm and 5°. Meanwhile, these members were assigned different wall thicknesses (t) to maintain the same weight (see Figure 1(a)).

The boundary and impact conditions applied to the conical members are illustrated in Figure 1(b). The bottom end of the members was clamped to the fully fixed plane in all directions, and the top end was modeled as free. Furthermore, a rigid wall modeled by MAT-RIGID code (it must be noticed that the rigid bodies are modeled by this code in LS-DYNA) with an added mass (m_a) of 600 kg and an initial velocity (v₀) of 15 m/s impacted vertically on the top end of the conical members at different incident angles α={0°, 10°, 20°, 30°}. The material of these members was set to be aluminum alloy AA6060-T4 due to having greater strength to weight ratio compared with other materials like steels. AA6060-T4 has the following mechanical properties: yield stress s_y=80 MPa, ultimate stress s_u=173 MPa, elastic modulus E=68.2 GPa, density r=2700 kg/m³ and Poisson ratio υ=0.33. The stress-strain curves of AA6060-T4 have been given in Figure 2.

3 Validation of numerical simulations

Before performing the numerical simulations in LS-DYNA, it was required to validate the finite element results by comparing them with the experimental data. For this purpose, experiments were carried out on the circular tubes using the universal test machine shown in Figure 3. The circular tubes with diameter of 50 mm, length of 90 mm, and wall thickness of 2 mm were placed on the lower fixture, and the upper fixture with angles of 0° and 8° was moved downwards with a constant velocity of 10 mm/min. Variations of load versus the cross-head displacement were recorded by a personal computer connected to the universal test machine. Meanwhile, two specimens were tested for each loading angle. These tubes were then modeled and analyzed in LS-DYNA as the same as the experimental conditions. Steps of deformation mode with α=0° are shown in Figure 3. Results of both experimental and numerical are presented in Table 1 and Figure 4. As the figure illustrates, there is a good agreement between the numerical and experimental results in terms of collapse modes and force–displacement curves. Therefore, the numerical models can simulate the crushing process of the tubes with sufficient accuracy.

Figure 1 Sectional configurations (A-A section) assumed for double-walled conical tubes (a), and boundary and impact conditions applied in FE modeling (b)

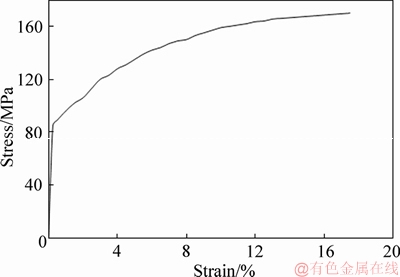
Figure 2 Stress-strain curve of AA6060-T4

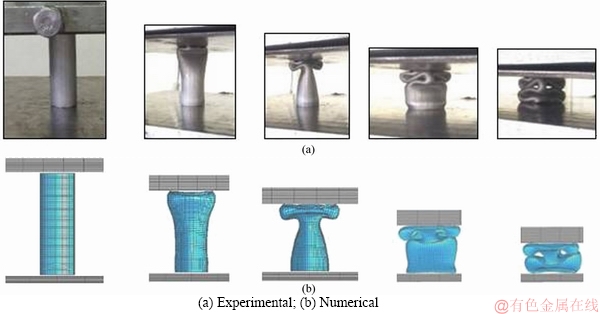
Figure 3 Steps of deformation mode with α=0°:

Table 1 Experimental and numerical results for circular tubes collapsed at different loading angles

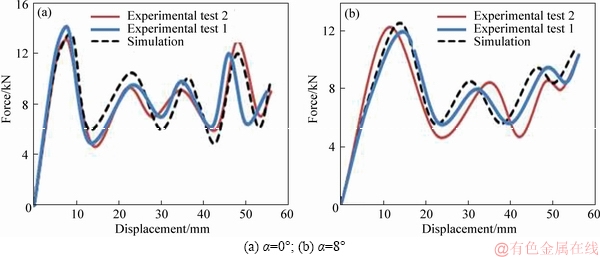
Figure 4 Comparison of experimental and numerical results:

To further validate the numerical modeling, the experiments were performed on the double-walled circular tubes including four stiffeners under axial loading as shown in Figure 5. The radii of the outer and inner circles were 23 and 12 mm, and the length and thickness of each double-walled tube were 68 and 2 mm, respectively. The material of these tubes was AA6060-T4, and the mechanical properties of which were listed in Section 2. The procedure of performing the experiments was such that the tubes were fixed on the lower support and the upper support was moved downwards with a speed of 10 mm/min. Variations of the force versus the displacement were then extracted from the experiments. The experimental and numerical results are shown in Figure 5. As can be seen, the finite element analyses correctly predicted the collapse modes, and the force-displacement curves in simulation agreed well with those of experimental.

4 Crashworthiness comparisons of different multi-cell conical tubes

4.1 Crashworthiness criteria

EA is an important crashworthiness indicator which is frequently used as the main criteria for stating energy absorption capacity of columns. A suitable thin-walled member must have higher value of EA which is simply measured as

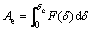                          (1)

where δ_c is the maximum displacement moved by the rigid-wall which was assumed to be 165 mm in the present work. F(δ) is variation of the collapse load versus the rigid-wall displacement, and δ is defined as the rigid-wall displacement. Indeed, EA is the area under the collapse force-displacement curve.

Sometimes, the non-same weight columns are required to be compared in terms of crashworthiness. To take account of the amount of weight in the energy absorption performance, the specific energy absorption (SEA, A_se) is employed. SEA is defined as below, where m is mass of the crushed structure.

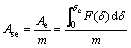                     (2)

Another key crashworthiness indicator is PCF which is defined as the maximum force achieved in the collapse load-displacement curve. This parameter is attempted to be reduced for the safety sake of vehicle passengers. Thus, the less the PCF value, the better the column in terms of the crashworthiness capacity.

4.2 Numerical results

The conical structures illustrated in Figure 1 were analyzed in LS-DYNA under various impact angles α={0°, 10°, 20°, 30°}. Table 2 depicts the deformation modes of these structures under different impact loads. For comparison purposes, all these structures were crushed identically over 165 mm (i.e., about 66% of the total length). From Table 2, it is obvious that all the structures have been progressively deformed in diamond mode under axial loading due to the presence of the ribs that connected the internal tube to the external one. Moreover, the ribs caused these structures to crush asymmetrically. When the structures were subjected to the small oblique load at 10°, they still collapsed in diamond mode similar to the one observed for the axial loading.

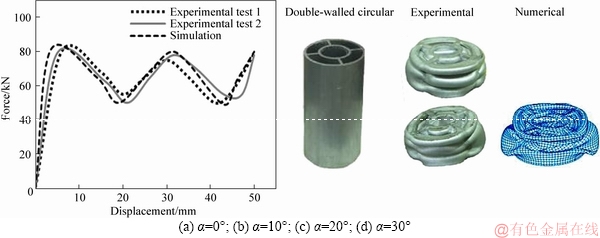
Figure 5 Comparison of experimental and numerical results for double-walled circular tubes

Table 2 Deformation modes of conical structures under different impact loads

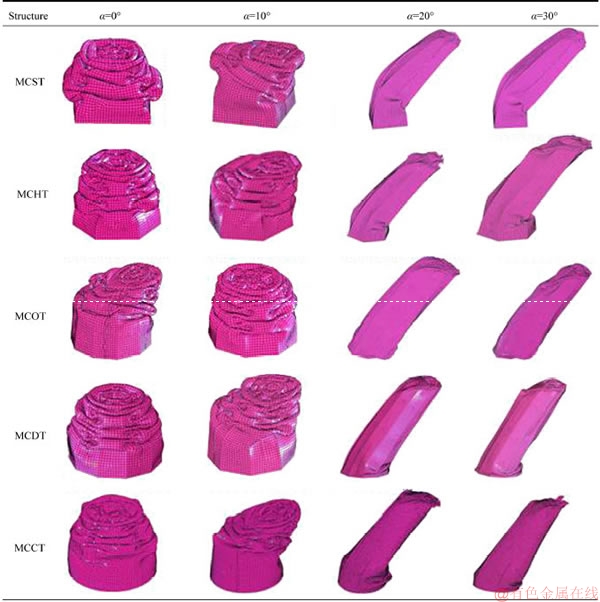
For the larger oblique loads at 20° and 30°, the structures were deformed in the less effective global bending mode. Manifestly, the useful progressive folding mode was no longer observed, and all the structures dissipated the rigid wall energy by global bending at the region near to the bottom end. It is preferable for the tubes to be impacted axially and axial impacts bring about collapse by progressive folding, which has been found to absorb higher energy. Nevertheless, the pure axial impact condition is rarely observed in collision events, so the oblique impact is inevitable during a crash.

The relationships between impact force and rigid wall displacement extracted from the LS-DYNA simulations for the conical tubes are given in Figure 6. For the axial loading case, the force initially increased sharply to reach its first peak once the first fold was formed, and then oscillated to reach its second peak corresponding to the second fold. Afterwards, the force oscillated several times about the mean dynamic force due to forming the following folds. As is seen in Figure 5, the second peak was larger than the first one, unlike the trend observed for the straight tubes, in which the first peak is larger than the subsequent ones [38-40].

This behavior of the conical tubes is imputed to the gradual increase of their cross-section area that caused the gradual increase in force, and so resulted in the smaller first peak force. This issue can be considered an advantage for the conical tubes as it avoids exerting fatal forces upon the passengers. The trends of the force variations versus the rigid wall displacements for the small oblique load at 10° were similar to the trends observed for the axial loading, with the difference that the force initially enhanced with less steep. This is because the rigid wall impacted the partial cross-sectional area of the tubes at the start of the oblique loading. Under larger oblique loads of 20° and 30°, the force firstly increased to the peak point, and then gently decreased. This behavior corresponds with the global bending taking place at the bottom end of the conical tubes (see Table 2).

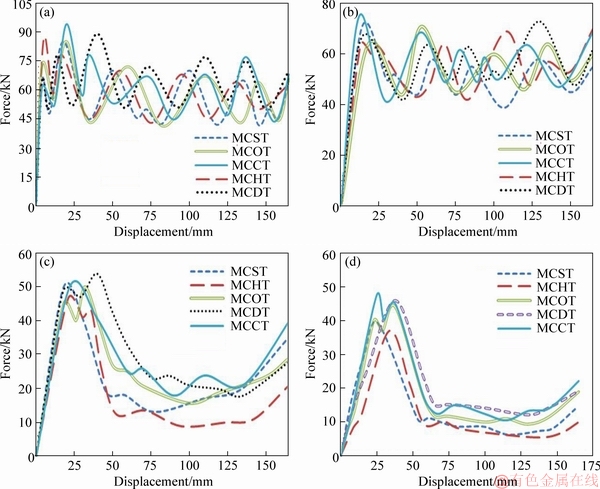
Figure 6 Force-displacement curves of conical structures for impact angles:

The area under the force-displacement curves was calculated according to Eq. (1) to obtain the energy absorbed by the conical structures as presented in Figure 7, from which, the structures behaved differently at different loadings, and generally MCDT and MCHT cross-sections respectively achieved the most and the least energy absorption capacity, taking account of all the impact angles.

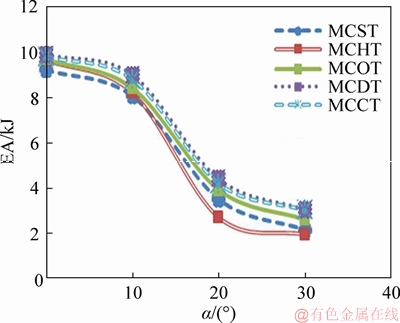
Figure 7 Energy absorbed by multi-cell conical structures under various impact loads

This result appears to be related to the number of corners and ribs, such that the tubes with greater numbers of corners and ribs demonstrated improved resistance against deformation. Among these, the EA is affected more by the number of ribs than the number of corners. Hence, the tubes with decagonal (with 5 ribs and 40 corners) and hexagonal (with 3 ribs and 24 corners) cross-sections were found to be the best and worst energy absorbers, respectively.

The peak collapse forces extracted from the force-displacement curves for the conical tubes are given in Figure 8, in which, the PCF values decreased as the impact angle increased. This is because as impact angle increased, tube stiffness decreased, i.e., the bending mode required less energy than the folding mode. Meanwhile, MCCT and MCHT cross-sections generated on average the highest and lowest PCF, respectively, taking account of all the impact angles.

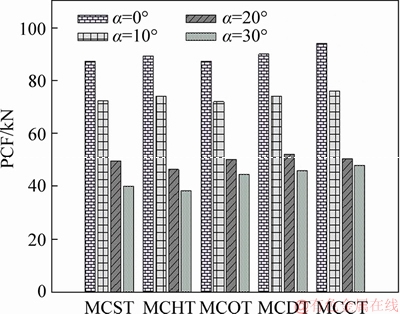
Figure 8 Peak collapse force for multi-cell conical tubes under different impact loads

4.3 Complex proportional assessment

Complex proportional assessment (COPRAS) is the ranking method used in many fields for selecting the better alternatives where there are more than one criterion. This method was developed by ZAVADSKAS et al [41-43] who considered significant available alternatives against the conflicting criteria. The process and formulation of COPRAS on the available alternatives and criteria can be found in Ref. [44] in detail.

Since there are 8 criteria (4 impact angles in each crashworthiness indicators EA and PCF) in the present work, the COPRAS method can be used to make suitable decisions to select an appropriate energy absorber. This method was applied to the numerical results presented in Section 4.2 based on the aforementioned steps. It is well known that an energy absorber used in a safe space frame must have greater EA values and smaller PCF values. In addition, because the EA is more important than the PCF, their weightings were set to 0.6 and 0.4, respectively, in the COPRAS calculations. Accordingly, the decision matrix for the five alternatives investigated in the present task was constructed as seen in Table 3. The normalized decision matrix was then computed (see Table 4). The ranking of the alternatives was finally obtained: MCDT > MCCT > MCOT > MCST > MCHT (see Table 5). As a result, the multi-cell conical tube with decagonal cross sectional shape was selected as the best energy absorbing device, and this is due to possessing more corners and ribs.

4.4 Decagonal conical tubes with different inside ribs

MCDT was found to be the best energy absorber as described in Section 4.3. The effects of the number of inside ribs on the crashworthiness of this tube are evaluated. Four different types of decagonal conical tubes were considered, shown in Figure 9. The ratio of the internal tube size to the external one, the perimeter of the external tube at the small end, the total length, and the conic angle were set to 0.5, 80 mm, 250 mm and 5°, respectively. These tubes were assigned different wall thicknesses to maintain the same weight (see Figure 9). The material and the boundary and impact conditions applied to these tubes were mentioned in Section 2. These tubes were analyzed in LS-DYNA under different loading angles, and for brevity, only the calculated criteria (EA and PCF) together with the COPRAS results have been given in Tables 6-8. The COPRAS results displayed that the decagonal conical tubes ranked as Type 2 > Type 3 > Type 4 > Type 1. In other words, as the number of ribs increased, the decagonal tube performed better. Furthermore, the decagonal tube with five ribs connecting the middle of the internal wall to the external one was found as the best energy absorbing device. Meanwhile, the tubelabeled Type 1 had the worst performance due tohaving no rib.

Table 3 Decision matrix in COPRAS calculations for conical tubes

Table 4 Normalized decision matrix in COPRAS calculations for conical tubes

Table 5 Ranking results obtained from COPRAS calculations for conical tubes

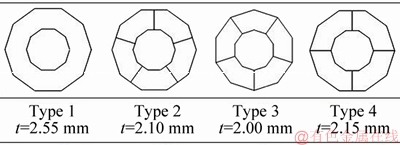
Figure 9 Sectional configurations assumed for decagonal conical tubes

Table 6 Decision matrix in COPRAS calculations for decagonal tubes with different sectional shapes

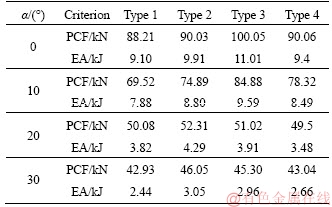
Table 7 Normalized decision matrix in COPRAS calculations for decagonal tubes with different sectional shapes

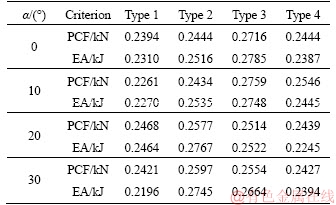
Table 8 Ranking resects obtained from COPRAS calculation for decagonal tubes with different sectional shapes

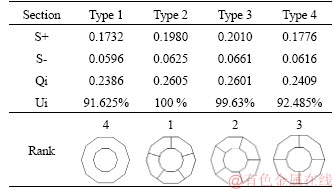
5 Crashworthiness optimization of MCDT

5.1 Problem description

MCDT was selected as the best energy absorbing device, as mentioned above. More attempts are made to obtain an optimal design of MCDT using artificial neural networks. The flowchart of the optimization is given in Figure 10. Two main criteria, namely SEA and PCF, together with four loading angles 0°, 10°, 20° and 30° were utilized for evaluating the conical tubes. Meanwhile, a desirable energy absorber is expected to have higher capacity of SEA and smaller PCF as much as possible. The optimization problem can be mathematically written as Eq. (3) for different loading angles, in which, the beneficial criterion (i.e. SEA) must be maximized while the non- beneficial criterion (i.e. PCF) must be minimized. In addition, the cone angle θ and ratio of the internal tube size to the external one S (as shown in Figure 1(b)) were considered designed variables in the optimization problem.

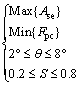                            (3)

In order to clarify the optimization work performed in this research, it is briefly explained according to the flowchart shown in Figure 10. At the first step, sampling points from the space of design variables (namely 0.2≤S≤0.8 and 2°≤q≤8°) are determined using design of experimental method. These sampling points are seen in Table 9. The decagonal structures generated by the geometries offered by sampling points are then simulated in LS-DYNA (according to the impact and boundary conditions described in Section 2) under various loading angles of 0°, 10°, 20° and 30° to compute the crashworthiness criteria including SEA and PCF. Afterwards, the neural network is built using the input (i.e. S and q) and output (i.e. SEA and PCF) values to derive objective functions for the crashworthiness criteria (i.e. SEA and PCF), separately. In other words, the objective functions are obtained for the SEA and PCF (for each of the loading angle) in terms of the design variables of S and q. If the responses of these functions are accurate, the optimum points of S and q will be obtained using the genetic algorithm by maximizing and minimizing objective functions of SEA and PCF, respectively, as mentioned in Eq. (3). Otherwise, a new sampling point from the space of design variables (S and q) presented in Table 9 is chosen. This process is repeated several times until the proper values of optimum points are obtained. The mentioned steps are generally called as training process for generating the suitable neural networks.

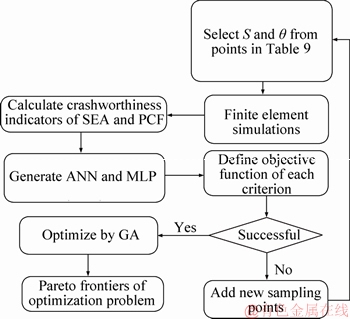
Figure 10 Flowchart of optimization method

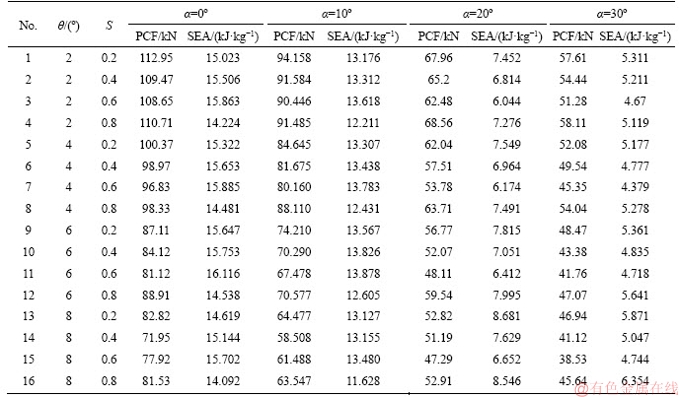
Table 9 Numerical results used in training algorithm

5.2 Artificial neural network

Artificial neural networks are considered a powerful technique to model complex input-output systems [45, 46]. Elements in the neural networks operate in parallel, and due to remarkable ability of the neural networks, they can deal with nonlinear modeling for which an accurate analytical solution is difficult to obtain [47]. These elements, called neurons, have been inspired by the human brain physiology [48]. The relations between these elements characterize the network function. Generally, ANNs comprise three types of layer: a layer of input neurons, a layer of output neurons and layers of hidden neurons [49]. Neurons in each layer are connected to previous and subsequent layers. ANNs are classified into several types, of which the learning algorithm is the most popular one [50]. A neural network can be trained to perform a particular function by adjusting the values of the connections (weights) between elements. In other words, neural networks are trained and thus a particular input can lead to a desirable output. The aim of training algorithm is to minimize the error between the target output and the network output.

Different categories exist for ANNs. There are two main types, which are supervised and unsupervised. The multi-layer perceptron and Kohonen self-organizing feature are the frequently used ANNs for supervised and unsupervised categories, respectively [51]. The most extensively used neural network, multi-layer perceptron (MLP), was employed in this research study. The design steps of an efficient multi-layer perceptron network are described below.

1) Determination of the input and output data based on dataset. Data for the parameters of θ and S were used as the input data. The data for the SEA and PCF at multiple loading angles were chosen as the output data. Table 9 shows the data used in the present research for the MCDT. The ranges for the values of θ and S (shown in Table 9) were selected to be 2° to 8° (similar to the previous investigations like [34, 52]) and 0.2 to 0.8 (see Refs. [18, 53]), respectively.

2) Division of the data into several parts to train, validate and test the constructed network. In this research, 70% of the data shown in Table 9 were used for training and the remaining 30% were used to test the constructed network. Finally, all the data were used to validate the constructed network. The main reason for this division is to prevent overfitting which is one of the important drawbacks of ANN [45]. It is noted that the learning process was accomplished by the Levenberg-Marquardt back-propagation method [45] training with the Trainlm algorithm.

It is worth noting that the mentioned sampling (training/validating) points presented in Table 9 were generated based on a four-level full factorial design of experiments method. There are many design of experiments methods, such as the factorial, Koshal, composite, Latin Hypercube, D-optimal [52] to select the sampling points from the assumed range of the design variables (S and θ). In this research, 16 sampling points distributed in the design domain were selected as seen in Table 9. The responses of SEA and PCF for the conical tubes generated from these 16 sampling points were obtained by numerical analyses in LS-DYNA (see Table 9). As mentioned above, only 70% of the sampling points were used for training the constructed ANN to obtain the objective functions.

3) Construction of various networks by changing the numbers of hidden neurons and of activation functions. A typical ANN block diagram used in the present work has been depicted in Figure 11. The network included two hidden layers, each with seven neurons. The hyperbolic tangent and logarithmic sigmoid functions were taken as the activation functions for the first and second hidden layers, respectively. Moreover, linear functions were used for the output layer. 98 networks were created for each crashworthiness indicator, and generally 784 networks were constructed for all the impact angles.

4) Assessment of the performance of the constructed networks by mean square error (MSE). Note that to calculate MSE, an inverse range scaling was made for returning the outputs to their original scale [54]. MSE can be calculated as follows:

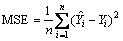                      (4)

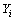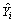where n,andcorrespond to the total number of data (16 herein), numerical results, and network output, respectively. The calculated MSE of the crashworthiness indicators for the constructed networks have been presented in Figure 12. Comparison of the predicted and numerical results (Figure 12) reveals that the created networks have a good level of accuracy; therefore, the constructed networks can be employed for predicting the crashworthiness indicators.

5.3 Multi-objective optimization

Multi-objective optimization was used to find the maximum objective function by adjusting θ and S. The objective functions were derived from the ANN to determine the complicated nonlinear relationship between the design variables and crashworthiness parameters. Combined ANN with GA, ANN-GA was used in the present task to optimize θ and S of the multi-cell conical tube with decagonal cross-section. In other words, multi- objective optimization was performed using the genetic algorithm with trained neural networks to characterize the optimum values of θ and S.

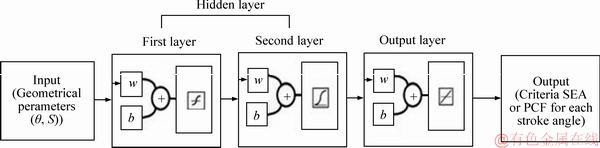
Figure 11 Typical ANN block diagram used in present work

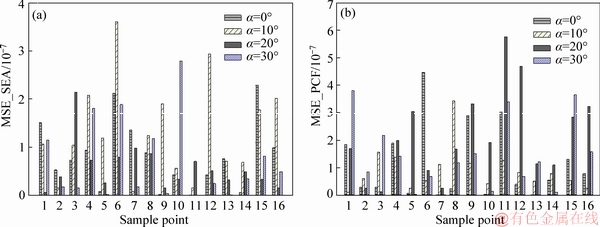
Figure 12 MSE of crashworthiness indicators for created networks

There are many multi-objective optimization algorithms, such as GA [55-57] and Pease [58, 59]. The GA technique was employed in the present work to generate the Pareto curves for the optimization problem defined in Eq. (3). The GA technique is heuristic search algorithm inspired by the evolutionary concept of Darwin’s theory. The GA represents an intelligent exploitation of a random search utilized to solve optimization problems. The GA exploits historical information to direct the search into the region of better performance within the search space [60, 61].

The optimization was conducted for different single loading angles (0°, 10°, 20° and 30°) separately, i.e., only one loading angle was considered in each case.

Figure 13 shows the Pareto curves for these different loading angles. The Pareto curves (shown in Figure 13) have been expressed in terms of two conflicting criteria, SEA and PCF, implying that one of these criteria cannot be further improved without a trade-off with the other one. Both the minimum distance selection (MDS) method [62] and COPRAS method were adopted to characterize the knee points for different loading angles. According to Figure 13, α and β represent the knee points extracted from the MDS and COPRAS results, respectively. Thus, the optimum MCDT configurations (θ and S) together with the corresponding values of SEA and PCF predicted by the ANN-GA models have been provided in Table 10.

These eight points indeed correspond to the knee points shown in Figure 13. In order to further consider the accuracy of results predicted by ANN-GA models (namely SEA and PCF), these eight MCDTs were simulated in LS-DYNA. As provided in Table 10, the errors between the ANN-GA and LS-DYNA results were on average about 1%. Meanwhile, the errors were greater for PCF than for SEA, and the errors for the results extracted from the MDS method were less than those of COPRAS.

Though the Pareto curves illustrated in Figure 13 for single loading angles are of important implication, the obtained optimum MCDT configuration for one single loading angle may not efficiently perform under other loading angles. Consequently, the optimization was performed on the MCDT by taking account of the effects of all the loading angles simultaneously. There are some investigations in the literature on this issue. For example, ZHANG et al [63] optimized the dynamic responses and energy absorption of foam-filled conical tubes under axial and oblique impact loading conditions by using a D-optimal design of experiments and a kriging model. QIU et al [18] optimized the crashworthiness of hexagonal columns under multiple loading cases by using a Kriging model.

Two criteria (SEA and PCF) were used in conducting the optimization for the single loading angle as discussed above. In order to find the optimum geometry of MCDT by considering all loading angles, 8 criteria namely SEA^α=0°, PCF^α=0°, SEA^α=10°, PCF^α=10°, SEA^α=20°, PCF^α=20°, SEA^α=30°, and PCF^α=30° were selected. θ and S were considered design variables in the optimization problem. In the following step, eight objective functions corresponding to the mentioned 8 criteria were obtained from the ANN-GA analyses. The objective functions corresponding to the beneficial criterion (i.e. SEA) must be maximized while those corresponding to the non-beneficial criterion (i.e. PCF) must be minimized in the optimization process. Weighting factors for different loading angles can influence the results of multi-objective optimization significantly. The weighting factors for multiple loading angles must be chosen according to the occurrence probabilities of a collision scenario in a real condition [64]. However, the weighting factors were selected to be the same (equal to 0.25) for all the loading angles in the present paper.

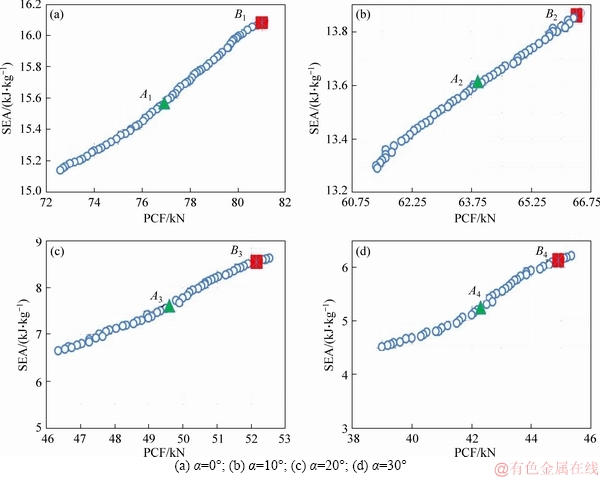
Figure 13 Pareto curves for two-objective optimization under loading angles:

Table 10 Optimum MCDT configurations predicted by ANN-GA and corresponding values of SEA and PCF

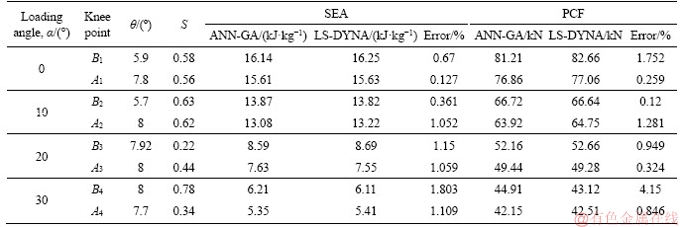
Figure 14 displays the Pareto curves, in terms of SEA and PCF, for this case. The knee points resulting from the MDS and COPRAS methods are depicted in Figure 14 as well.

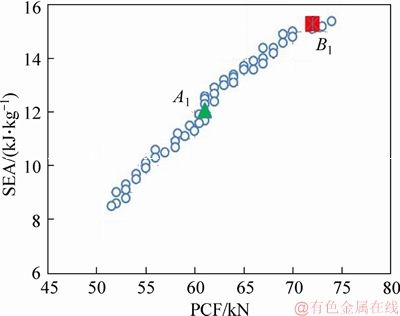
Figure 14 Pareto curves for MCDT by considering all loading angles

Specifications of these points are listed in Table 11. As a result, the optimum values were found to be θ=7.9°, S=0.46 and θ=8°, S=0.74 based on the MDS and COPRAS methods, respectively. Therefore, MCDT with the mentioned optimum configuration can perform well to absorb collision energy, and thus can improve the safety of the vehicles efficiently. It is worth mentioning that we considered respective weightings of 0.4 and 0.6 for the PCF and EA respectively, to select the best geometry (or to find the optimum values) in the COPRAS calculations. The reason for this decision is that the crashworthiness indicator, EA, is more important than the PCF in the design of energy absorbers.

Meanwhile, the obtained optimum values from the ANN-GA methods were validated by analyzing the tubes in LS-DYNA. As is seen in Table 11, the differences between the values of SEA and PCF extracted from the ANN-GA and LS-DYNA are reasonable, which indicates accuracy of the predictions by ANN-GA methods.

6 Conclusions

In the present study, the crashworthiness performance of five different multi-cell conical tubes (i.e., MCST, MCHT, MCOT, MCDT and MCCT) reinforced with several inside ribs were evaluated under axial and three oblique loading angles. Nonlinear finite element code LS-DYNA was used to perform the numerical simulations. After validating these simulations with experimental data, the mentioned multi-cell conical tubes were analyzed in LS-DYNA and the crashworthiness criteria (EA and PCF) were calculated. The COPRAS method was then implemented on the numerical results to select the best sectional configuration from the crashworthiness point of view. In the COPRAS calculations, MCDT showed the best performance. Furthermore, the finite element results demonstrated that all the structures were folded progressively in diamond mode under axial loading. They still collapsed in diamond mode under the loading angle of 10°.

For the larger oblique loads at 20° and 30°, the structures were deformed in the less effective global bending mode. Furthermore, the effects of possible number of inside ribs on the crashworthiness of the decagonal conical tubes were also evaluated, and the results displayed that the tubes performed better as the number of ribs increased.

In the next stage of the present study, MCDT was optimized using ANN-GA methods. In other words, the multi-objective optimization was established using the genetic algorithm with trained artificial neural networks to characterize the Pareto curves. The optimum values of cone angle (θ) and ratio of the internal tube size to the external one (S) were then obtained through two approaches: the individual loading angle, and taking account of all the loading angles simultaneously. The second approach was applied because the optimal tube obtained from the first approach may perform worse when subjecting to other loading angles.

Meanwhile, the optimal tube obtained from the second approach can generally perform well under any single loading angle. It is worth mentioning that either the minimum distance selection method or COPRAS method was adopted for obtaining the optimum tube configuration.

Table 11 Specifications of knee points for MCDT by considering all loading angles

References

[1] Hosseini-Tehrani P, Pirmohammad S. Collapse study of thin-walled polygonal section columns subjected to oblique loads [J]. Proc Inst Mech Eng, Part D: J Automobile Eng, 2007, 221(7): 801-810.

[2] Elmarakbi A, Long Y X, MacIntyre J. Crash analysis and energy absorption characteristics of S-shaped longitudinal members [J]. Thin-Walled Struct, 2013, 68: 65-74.

[3] Zou X, Gao G, Zhang J, Zhou X, Chen W, Guan W. A comparative crashworthiness analysis of multi-cell polygonal tubes under axial and oblique loads [J]. Journal of Central South University, 2017, 24(9): 2198-2208.

[4] Hosseini-Tehrani P, Nikahd M. Effects of ribs on S-frame crashworthiness [J]. Proc Inst Mech Eng, Part D: J Automobile Eng, 2006, 220: 1679-1689.

[5] Hosseini-Tehrani P, Nikahd M. Two materials S-frame representation for improving crashworthiness and lightening [J]. Thin-Walled Struct, 2006, 44: 407-414.

[6] Eyvazian A, Mozafari H, Hamouda A M. Experimental study of corrugated metal-composite tubes under axial loading [J]. Procedia Eng, 2017, 173: 1314-1321.

[7] Marzbanrad J, Mashadi B, Afkar A, Pahlavani M. Dynamic rupture and crushing of an extruded tube using artificial neural network (ANN) approximation method [J]. Journal of Central South University, 2016, 23(4): 869-879.

[8] Pirmohammad S, Esmaeili-Marzdashti S. Crashworthiness optimization of combined straight-tapered tubes using genetic algorithm and neural networks [J]. Thin-Walled Struct, 2018, 127: 318-332.

[9] Oliveira D A, Worswick M J, Grantab R, Williams B W, Mayer R. Effect of forming process variables on the crashworthiness of aluminum alloy tubes [J]. Int J Impact Eng, 2006, 32(5): 826-846.

[10] Hanssen A G, Langseth M, Hopperstad O S. Static and dynamic crushing of square aluminium extrusions with aluminium foam filler [J]. Int J Impact Eng, 2000, 24(4): 347-383.

[11] Hanssen A G, Langseth M, Hopperstad O S. Static crushing of square aluminium extrusions with aluminium foam filler [J]. Int J Mech Sci, 1999, 41(8): 967-993.

[12] Seitzberger M, Rammerstorfer F G, Degischer H P, Gradinger R. Crushing of axially compressed steel tubes filled with aluminium foam [J]. Acta Mech, 1997, 125(1-4): 93-105.

[13] Seitzberger M, Rammerstorfer F G, Gradinger R, Degischer H, Blaimschein M, Walch C. Experimental studies on the quasi-static axial crushing of steel columns filled with aluminium foam [J]. Int J Solids Struct, 2000, 37: 4125-4147.

[14] Song J, Guo F. A comparative study on the windowed and multi-cell square tubes under axial and oblique loading [J]. Thin-Walled Struct, 2013, 66: 9-14.

[15] Ghamarian A, Zarei H R, Abadi M T. Experimental and numerical crashworthiness investigation of empty and foam-filled end-capped conical tubes [J]. Thin-Walled Struct, 2011, 49: 1312-1319.

[16] Qiu N, Gao Y, Fang J, Feng Z, Sun G, Li Q. Theoretical prediction and optimization of multi-cell hexagonal tubes under axial crashing [J]. Thin-Walled Struct, 2016, 102: 111-121.

[17] Najafi A, Rais-Rohani M. Influence of cross-sectional geometry on crush characteristics of multi-cell prismatic columns [C]// 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. 2008.

[18] Qiu N, Gao Y, Fang J, Feng Z, Sun G, Li Q. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases [J]. Finite Elem Anal Des, 2015, 104: 89-101.

[19] Song X G, Sun G Y, Li G Y, Gao W Z, Li Q. Crashworthiness optimization of foam-filled tapered thin-walled structure using multiple surrogate models [J]. Struct Multidisc Optimiz, 2013, 47(2): 221-231.

[20] Wu S, Zheng G, Sun G, Liu Q, Li G. On design of multi-cell thin-walled structures for crashworthiness [J]. Int J Impact Eng, 2016, 88: 102-117.

[21] Sun G, Liu T, Fang J, Steven G P, Li Q. Configurational optimization of multi-cell topologies for multiple oblique loads [J]. Struct Multidisc Optimiz, 2018, 57(2): 469-488.

[22] Zhang X, Cheng G. A comparative study of energy absorption characteristics of foam-filled and multi-cell square columns [J]. Int J Impact Eng, 2007, 34: 1739-1752.

[23] Zhang X, Cheng G, Wang B, Zhang H. Optimum design for energy absorption of bitubal hexagonal columns with honeycomb core [J]. Int J Crashworthiness, 2008, 13(1): 99-107.

[24] Hosseini-Tehrani P, Pirmohammad S. Study on crashworthiness characteristics of several concentric thin wall tubes [C]// ASME 2010 10th Biennial Conference on Engineering Systems Design and Analysis. Istanbul, Turkey, 2010, 3: 1-8.

[25] Zhang Y, Sun G, Li G, Luo Z, Li Q. Optimization of foam-filled bitubal structures for crashworthiness criteria [J]. Materials & Design, 2012, 38: 99-109.

[26] Fang J, Gao Y, Sun G, Zhang Y, LI Q. Crashworthiness design of foam-filled bitubal structures with uncertainty [J]. Int J Non-Linear Mech, 2014, 67: 120-132.

[27] Djamaluddin F, Abdullah S, Ariffin A.K, Nopiah Z M. Non-linear finite element analysis of bitubal circular tubes for progressive and bending collapses [J]. Int J Mech Sci, 2015, 99: 228-236.

[28] Sharifi S, Shakeri M, Ebrahimi H, Bodaghi M. Experimental investigation of bitubal circular energy absorbers under quasi-static axial load [J]. Thin-Walled Struct, 2015, 89: 42-53.

[29] LI Jian, GAO Guang-jun, ZOU Xiang, GUAN Wei-yuan. Crushing analysis and multiobjective crashworthiness optimization of bitubular polygonal tubes with internal walls [J]. Journal of Central South University, 2016, 23(11): 3040-3050.

[30] Ahmad Z, Thambiratnam D P. Crushing response of foam-filled conical tubes under quasi-static axial loading [J]. Materials & Design, 2009, 30(7): 2393-2403.

[31] Ahmad Z, Thambiratnam D P. Dynamic computer simulation and energy absorption of foam-filled conical tubes under axial impact loading [J]. Comput and Struct, 2009, 87(3, 4): 186-197.

[32] Ahmad Z, Thambiratnam D P, Tan A C. Dynamic energy absorption characteristics of foam-filled conical tubes under oblique impact loading [J]. Int J Impact Eng, 2010, 37(5): 475-488.

[33] Ghamarian A, Zarei H R, Abadi M T. Experimental and numerical crashworthiness investigation of empty and foam-filled end-capped conical tubes [J]. Int J Impact Eng, 2011, 49(10): 1312-1319.

[34] Hou S, Han X, Sun G, Long S, Li W, Yang X, Li Q. Multiobjective optimization for tapered circular tubes [J]. Thin-Walled Struct, 2011, 49(7): 855-863.

[35] Pirmohammad S, Ekbatan M H, Esmaeili- Marzdashti S. Crashworthiness of double-cell conical tubes with different cross sections subjected to dynamic axial and oblique loads [J]. Journal of Central South University, 2018, 25(3): 632-645.

[36] QI C, YANG S, DONG F. Crushing analysis and multiobjective crashworthiness optimization of tapered square tubes under oblique impact loading [J]. Thin-Walled Struct, 2012, 59: 103-119.

[37] Hosseini-Tehrani P, Pirmohammad S, Golmohammadi M. Study on the collapse of tapered tubes subjected to oblique loads [J]. Proc Inst Mech Eng, Part D: J Automobile Eng, 2008, 222(11): 2025-2039.

[38] Pirmohammad S, Esmaeili-Marzdashti S E. Crushing behavior of new designed multi-cell members subjected to axial and oblique quasi-static loads [J]. Thin- Walled Struct, 2016, 108: 291-304.

[39] Mohsenizadeh S, Alipour R, Shokri Rad M, Farokhi Nejad A, Ahmad Z. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading [J]. Material & Design, 2015, 88: 258-268.

[40] Li Z, Zheng Z, Yu J, Guo L. Crashworthiness of foam-filled thin-walled circular tubes under dynamic bending [J]. Material & Design, 2013, 52: 1058-1064.

[41] Zavadskas E K, Kaklauskas A, Turskis Z, Tamoaitien J. Selection of the effective dwelling house walls by applying attributes values determined at intervals [J]. J Civil Eng Manage, 2008, 14(2): 85-93.

[42] Zavadskas E K, Turskis Z, Tamo aitiene J, Marina V. Multi criteria selection of project managers by applying grey criteria [J]. Technol Econ Dev Econ, 2008, 14(4): 462-477.

[43] Zavadskas E K, Kaklauskas A, Peldschus F, Turskis Z. Multi-attribute assessment of road design solutions by using the COPRAS method [J]. Balt J Road Bridg Eng, 2007, 2: 195-203.

[44] Esmaeili S, Pirmohamad S, Esmaeili S. Crashworthiness analysis of S-shaped structures under axial impact loading [J]. Lat Am J Solids Struct, 2017, 14(5): 743-764.

[45] Demuth H, Beale M, Hagan M. Neural network tool box^TM 6 user’s guide [M]. The Math Works, Inc, 2010.

[46] Rafiai H, Jafari A. Artificial neural networks as a basis for new generation of rock failure criteria [J]. Int J Rock Mech Mining Sci, 2011, 48(7): 1153-1159.

[47] Mahdi E S, El-Kadi H. Crushing behavior of laterally compressed composite elliptical tubes: Experiments and predictions using artificial neural networks [J]. Composite Struct, 2008, 83(4): 399-412.

[48] Mahdevari S, Torabi S R, Monjezi M. Application of artificial intelligence algorithms in predicting tunnel convergence to avoid TBM jamming phenomenon [J]. Int J Rock Mech Mining Sci, 2012, 55: 33-44.

[49] Schalkoff R J. Artificial neural networks [M]. New York: McGraw-Hill, 1997.

[50] Haykin S. Neural networks: a comprehensive foundation [M]. Canada: Prentice Hall, 1994.

[51] Ebrahimabadi A, azimipour M, Bahreini A. Prediction of roadheaders’ performance using artificial neural network approaches (MLP and KOSFM) [J]. J Rock Mech Geo Eng, 2015, 7(5): 573-583.

[52] Qi C, Yang S, Dong F. Crushing analysis and multiobjective crashworthiness optimization of tapered square tubes under oblique impact loading [J]. Thin-Walled Struct, 2012, 59: 103-119.

[53] Pirmohammad S, Nikkhah H. Crashworthiness investigation of bitubal columns reinforced with several inside ribs under axial and oblique impact loads [J]. proc Inst Mech Eng, Part D: J Auto Eng, 2018, 232(3): 367-383.

[54] Salari D, Daneshvar N, Aghazadeh F, Khataee A R. Application of artificial neural networks for modeling of the treatment of wastewater contaminated with methyl tert-butyl ether (MTBE) by UV/H₂O₂ process [J]. J Haz Mat, 2005, 125(1-3): 205-210.

[55] Nariman-zadeh N, Darvizeh A, Jamali A. Pareto optimization of energy absorption of square aluminum columns using multi-objective genetic algorithms [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Int J Eng Manuf, 2006, 220(2): 213-224.

[56] Etghani M M, Shojaeefard M H, KHALKHALI A, AKBARI M. A hybrid method of modified NSGA-II and TOPSIS to optimize performance and emissions of a diesel engine using biodiesel [J]. Applied Thermal Eng, 2013, 59(1, 2): 309-315.

[57] Khalkhali A, Khakshourania S, Nariman- zadeh N. A hybrid method of FEM, modified NSGAII and TOPSIS for structural optimization of sandwich panels with corrugated core [J]. J Sandwich Struct and Mat, 2014, 16(4): 398-417.

[58] Raquel C R, Naval P C. An effective use of crowding distance in multi-objective particles warm optimization [C]// Proceeding of the 7th Annual Conference on Genetic and Evolutionary Computation. 2005: 257-264.

[59] Liu D, Tan K C, Goh C K, Ho W K. A multi objective memetic algorithm based on particles warm optimization [J]. IEEE Trans Syst Man Cybern, Part B: Cybern, 2007, 37(1): 42-50.

[60] Melanie M. An introduction to genetic algorithms [M]. London: MIT Press, 1999.

[61] Gregory J E. Foundations of genetic algorithms [M]. Rawlins: Kaufmann Publishers,1991.

[62] Barakat S, Bani-Hani K, Taha M Q. Multi-objective reliability-based optimization of prestressed concrete beams [J]. Struct Safety, 2004, 26(3): 311-342.

[63] Zhang Y, SUN G, XU X, LI G, LI Q. Multiobjective crashworthiness optimization of hollow and conical tubes for multiple load cases [J]. Thin-Walled Struct, 2014, 82: 331-342.

[64] Li G, ZHANG Z, SUN G, HUANG X, LI Q. Comparison of functionally-graded structures under multiple loading angles [J]. Thin-Walled Struct, 2015, 94: 334-347.

(Edited by ZHENG Yu-tong)

中文导读

动态载荷下多元锥形结构的多目标优化

摘要：本文对采用新型截面结构设计(正方形、六边形、八边形、十边形和圆形)的多元锥管在轴向和三种不同斜向载荷作用下的耐撞性能进行了评价。利用LS-DYNA建立的有限元模型对相同重量的不同结构的锥管进行了对比研究。采用了复比例评估法(COPRAS)，利用峰值临界力(PCF)和能量吸收 (EA)两个相互矛盾的准则来选择最优管结构。从COPRAS计算结果可以看出，具有十边形截面的多元锥形管(MCDT)具有最优耐撞性能。评价了可能的内肋数对十边形截面锥形管耐撞性的影响，结果表明，随着内肋数的增加，十边形截面锥形管的耐撞性能得到增强。采用了人工神经网络(ANN)和遗传算法(GA)对MCDT的参数(锥角θ和内外管尺寸比S)进行了优化。基于多目标优化的结果，利用最小距离选择法(MDS)和COPRAS方法得到的最优尺寸分别是θ=7.9°，S=0.46和θ=8°，S=0.74。

关键词：防撞性；多元锥形管；轴向和斜向载荷；COPRAS；多目标优化

Foundation item: Project(660) supported by University of Mohaghegh Ardabili, Iran

Received date: 2018-03-31; Accepted date: 2018-11-14

Corresponding author: PIRMOHAMMAD Sadjad, PhD, Associate Professor; Tel: +98-4533517030; E-mail: s_pirmohammad@uma.ac.ir; ORCID: 0000-0003-1988-1058