CVT插电式混合动力汽车全局优化控制策略
杨官龙,秦大同,刘永刚,林毓培
(重庆大学 机械传动国家重点实验室,重庆,400044)
摘要:针对一款无级变速器(CVT)插电式混合动力汽车,采用瞬时优化算法对CVT的速比进行实时优化,将优化结果嵌套在动态规划算法中进行全局优化,获得发动机与电机的功率分配;采用误差反向传播(BP)神经网络对发动机与电机的工作点进行训练拟合,得到优化控制MAP图,用于循环工况的实时控制。在Matlab/Simulink仿真平台下建立模型进行仿真,结果表明:采用BP控制策略的能耗经济性在新欧洲行驶循环(NEDC)、城市测功器驾驶进程(UDDS)和高速路燃油经济测试(HWFET)循环工况下与门限值控制策略得到的结果相比,都有不同程度的提高。
关键词:插电式混合动力汽车;无级变速器;全局优化;BP神经网络;能耗经济性
中图分类号: U461.8 文献标志码:A 文章编号:1672-7207(2014)12-4194-07
Global optimization control strategy of CVT plug-in hybrid electric vehicle
YANG Guanlong, QIN Datong, LIU Yonggang, LIN Yupei
(The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)
Abstract: Aiming at a continuously variable transmission(CVT) plug-in hybrid electric vehicles, the real-time optimization results of CVT speed ratio are obtained by using the instantaneous optimization algorithm , which have been embedded in a dynamic programming algorithm for global optimization getting power distribution rules of engine and motor. The control MAPs for real-time control of the driving cycle have been obtained by using BP neural network training fitting. On the matlab/simulink platform, the optimization mode was built and simulated. Simulation results indicate that the energy consumption economy of BP control strategy have different degrees of improvement comparing with threshold control strategy under New European Driving Cycle(NEDC), Urban Dynamometer Driving Schedule (UDDS) and Highway Fuel Economy Test (HWFET) cycle conditions.
Key words: plug-in hybrid electric vehicle; continuously variable transmission(CVT); global optimization;BP neural network; energy consumption economy
控制策略对插电式混合动力电动汽车(PHEV)的能耗经济性有着至关重要的影响,是插电式混合动力电动汽车的研究热点之一。有关控制策略的优化方法有多种,其中等效消耗最小值控制策略(ECMS)和动态规划(DP)算法得到广泛的关注。Geng等[1]采用极小值原理对ECMS进行了求解,结果表明:ECMS能较大的提高燃油经济性;Chen等[2]分别对ECMS和DP算法进行了研究,结果表明:DP算法的优化效果更加明显;Yang等[3]采用DP研究了道路坡度以及未来工况的划分对能耗经济性和排放的影响;Gong等[4]采用DP算法加强对PHEV的电量消耗(CD)模式下电池荷电状态(SOC)下降幅度的控制,有效地改善了车辆的能耗经济性;张博等[5]应用DP全局优化算法对PHEV在不同行驶里程下的控制策略进行了全局优化,得到动力总成在典型循环工况下的全局最优控制规律以及不同行驶里程下的最优控制规律;Moura等[6-7]采用随机动态算法对比研究了PHEV电池SOC轨迹为混合模式和电量消耗维持模式对电池容量和能耗经济性的影响;Mojtaba等[8]采用DP算法研究了发动机冷热起动对PHEV能耗经济性的影响;舒红等[9]采用DP算法研究了模型预测控制策略对燃油经济性的影响。由文献分析可知,诸多研究者采用了DP算法对特定工况进行全局优化以最大限度的提高整车的能耗经济性,但没有对采用机械无级变速器(CVT)的插电式混合动力汽车进行过全局寻优,且由于DP算法的计算时间较长,不适合控制策略的在线实时控制;因此,本文作者针对一款新设计的并联式单电机CVT插电式混合动力汽车,融合瞬时优化和DP全局优化相结合的算法对PHEV进行了优化研究,得到特定工况下的最优控制规律;并针对DP算法无法用于在线实时控制的缺陷,采用误差反向传播(BP)神经网络对发动机与电机工作点进行拟合,提炼出适用于道路循环工况的控制策略规则。
1 PHEV动力系统模型
1.1 PHEV动力系统介绍
PHEV动力系统由发动机、ISG(Integrated Starter/Generator)电机、单向离合器C1(用来保证传动系统的转速不低于发动机的转速)、摩擦离合器C2(用于ISG电机启动发动机及传递发动机转矩)、CVT、差速器、电池组等部件组成,其构成如图1所示。
1.2 PHEV动力系统建模
根据图1可以得到动力总成部件之间的动力学关系:
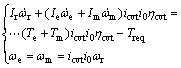 (1)
(1)
式中:Ir,Im和Ie分别为折算到车轮处、电机和发动机的转动惯量,kg·m2;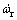 ,
,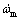 和
和 分别为车轮、电机和发动机的角加速度,rad/s2;icvt为CVT速比;i0为减速器速比;ηcvt为传动系效率;Tm为电机转矩,N·m;Te为发动机转矩,N·m;Treq为需求转矩,N·m;ωr,ωm和ωe分别为车轮、电机和发动机的转速,r/min。
分别为车轮、电机和发动机的角加速度,rad/s2;icvt为CVT速比;i0为减速器速比;ηcvt为传动系效率;Tm为电机转矩,N·m;Te为发动机转矩,N·m;Treq为需求转矩,N·m;ωr,ωm和ωe分别为车轮、电机和发动机的转速,r/min。
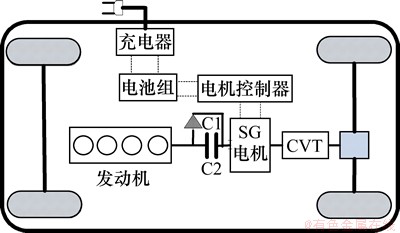
图1 单电机PHEV动力系统
Fig. 1 Powertrain of single motor PHEV
1.3 关键动力部件模型
1) 发动机和ISG电机模型。通过试验,利用3次样条插值拟合,得到发动机的油耗及电机效率数值模型,如图2和3所示。
2) 电池数学模型。电池SOC在充放电过程中的变化为
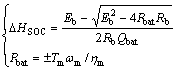 (2)
(2)
式中:ΔHSOC为电池SOC的变化值;Eb为电池电动势,V;Rb为电池的电阻,Ω;Qbat为电池组的容量,A·h;Pbat为电池消耗的功率,kW,放电过程中取正号,充电过程中取负号;ηm为电机的充放电效率。
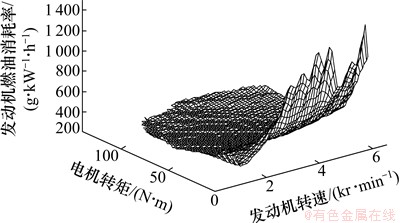
图2 发动机油耗数值模型
Fig. 2 Numerical model of engine fuel consumption
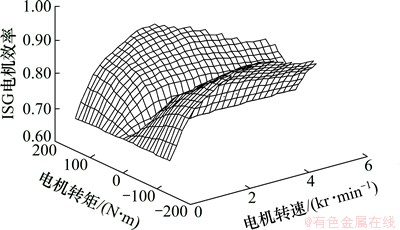
图3 ISG电机效率数值模型
Fig. 3 Numerical model of ISG efficiency
2 优化算法
针对动态规划增加状态变量会指数式增加计算时间的问题,本文优化算法的思路是将瞬时寻优与动态规划全局寻优相结合,采用瞬时优化算法对CVT的速比进行实时优化,进而将该实时优化结果嵌套在动态规划算法中对循环工况进行全局寻优。
2.1 瞬时优化算法
CVT车辆具有速比连续可变的特点,车辆在每个工作状态(SOC、车速、加速度、坡度)下必然存在一个最佳的目标速比可使能耗经济性最优。
PHEV 与普通意义上的混合动力汽车不同,其一部分能量来源于燃油,另一部分能量来源于电网充电,为了将这2种能量统一起来,本文中目标函数QC定义为2种能量消耗之和:
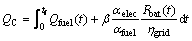 (3)
(3)
式中:tf为工况的终端时刻;αfuel和αelec为燃油与电消耗转化为MJ单位的转化系数;Qfuel(t)为t时刻消耗的燃油量,L/s;ηgrid为电网的充电效率,取0.98;Pbat(t)为t时刻电池的充放电功率,放电时大于0 kW,充电时小于0 kW;β为能量价格比,是一个可变参数,随着市场上油价和电价的波动而波动,可表示为
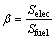 (4)
(4)
式中:Selec和Sfuel分别为每消耗1 MJ能量的电价和汽油的价格。
其中设计变量为icvt,约束条件为
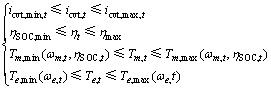 (5)
(5)
式中:ηSOC,t,ηSOC,min和ηSOC,max分别为电池荷电状态时刻、最小值与最大值。
瞬时优化算法计算流程如图4所示。
2.2 动态规划算法
动态规划作为一种多阶段决策问题的优化方法,可按时间或空间把问题分为若干个相互联系的阶段。具体到 PHEV 能量管理策略的优化问题上,应将选取的循环驾驶工况进行合理的离散化,这样整个循环工况的整车能耗最优控制问题就转换成为不同时间阶
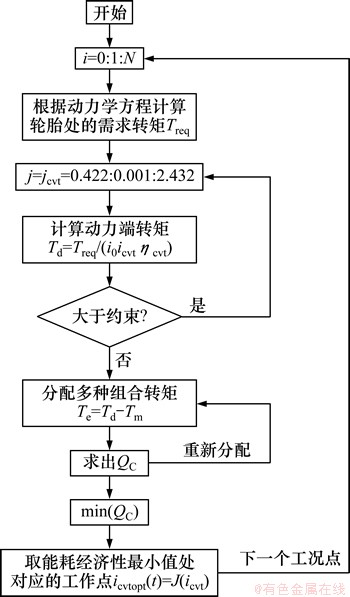
图4 瞬时优化计算流程
Fig. 4 Instantaneous optimization process
段的决策问题。
通过以上分析,将循环工况离散为k个阶段,优化函数为
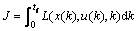 (6)
(6)
式中:x为状态变量;u为控制变量;L函数为k阶段的能耗经济性,即
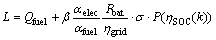 (7)
(7)
式中:σ为惩罚因子;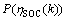 为惩罚函数,具体表示为
为惩罚函数,具体表示为
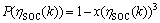 (8)
(8)
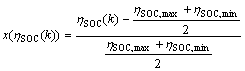 (9)
(9)
定义动力系统的状态变量为
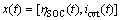 (10)
(10)
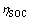 转移函数为
转移函数为
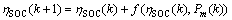 (11)
(11)
CVT速比的转移参考2.1节。
控制变量为
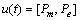 (12)
(12)
状态变量与控制变量的约束条件参考式(5)。
动态规划的基本示意图如图5所示。
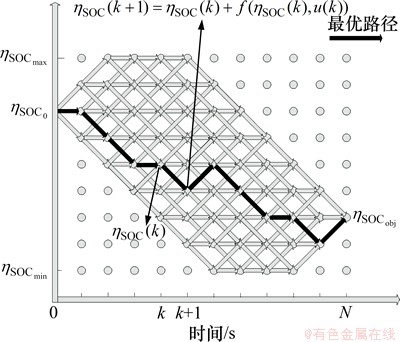
图5 动态规划求解示意图
Fig. 5 Schematic diagram of dynamic programming solving
3 优化结果及分析
国内常采用城市+城郊循环工况(New European Driving Cycle, NEDC)对车辆经济性进行评价,因此本文选取NEDC作为车辆的循环工况,如图6所示。
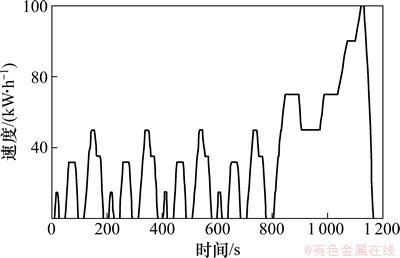
图6 NEDC循环工况
Fig. 6 NEDC driving condition
3.1 控制变量的优化结果及分析
为了更清楚地了解PHEV动力源的功率分配,将NEDC循环工况重复10次,经过优化算法计算,得到了发动机功率与电机功率的分布。图7给出了第1个和第10个NEDC工况的计算结果。可以看出,在第1个NEDC工况下,主要以电机作为主要动力输出源(通常所说的CD模式),在第10个工况下,以电机和发动机共同作为动力输出源(通常所说的CS模式)。
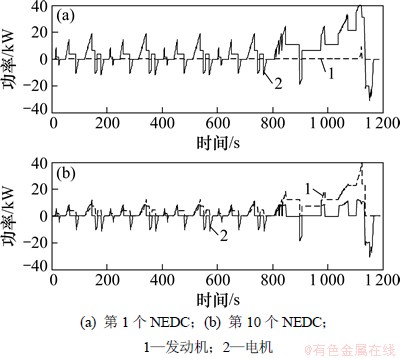
图7 发动机与电机功率的分布
Fig. 7 Power distribution of engine and motor
为了更清晰地了解电机和发动机的动力分配,图8与9分别给出了电机和发动机在不同模式下的工作点,可以看出:在CD模式下,电机工作的频率较高,基本都处于高效区,发动机只有少量工作点,发动机参与工作的原因为此时的转矩需求较大,超过了电机所能提供的最大转矩;在CS模式下,电机的工作点相对连贯(有些工作点对应于电机单独驱动,有些工作点对应于混合驱动),发动机的工作点较多且基本沿发动机的最佳经济性曲线工作,说明采用CVT和优化算法能对电机和发动机进行合理的控制,从而获得较好的能耗经济性。
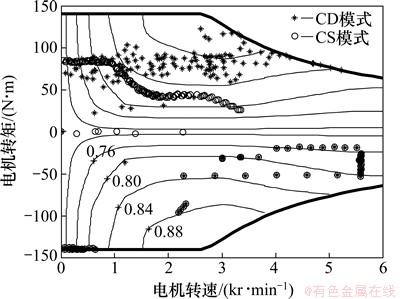
图8 电机的工作点
Fig. 8 Working point of motor
3.2 状态变量的计算结果及分析
经过路径优化,得到了CVT速比和电池SOC在不同工况点下的具体数值,如图10~11所示。从图10可以看出:CVT的状态点基本处于高效率区域,只是在CD与CS模式下的工作点不同,原因是在CS模式下发动机参与工作的次数增加。
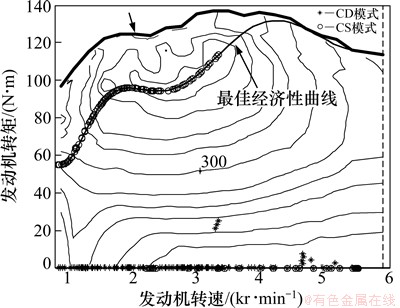
图9 发动机的工作点
Fig. 9 Working point of engine
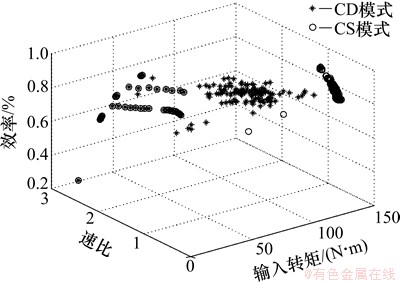
图10 CVT的状态点
Fig. 10 State point of CVT
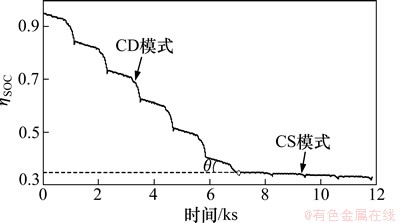
图11 电池SOC的状态变化曲线
Fig. 11 State curve of battery SOC
图11所示为电池SOC的状态转移轨迹,它按照CDCS工作模式的特性变化;为了更直观地了解电池SOC在CD模式的消耗速度,引入图11中所示的θ角来作为CD模式与CS模式的切换时刻,本次计算中为40.9°。
4 控制策略的数值拟合
上述优化算法存在计算量过大的问题,不能应用到实车上作为车辆的在线能量管理策略,但可以依据计算结果,对电机和发动机的工作点进行提取,从而制定出既符合 PHEV 特点又满足车辆能量管理实时性要求的在线能量管理策略。
4.1 基于BP神经网络的控制策略
采用BP神经网络分别对PHEV的CD和CS工作模式进行拟合,利用函数newff创建网络,设定网络输入层为车速和需求扭矩,输出层为电机和发动机的转矩,生成含有一个隐层的BP网络,神经元个数为30,定义隐含层传递函数为tansig,输出层传递函数为purelin,训练函数为train。
将10个NEDC工况(11 850个工作点)仿真结果中的11 450个工作点作为训练点,400个工作点作为验证拟合精度的高低,如图12~15所示。由图12~15可以看出:拟合输出与期望输出比较接近,在可接受范围之内。
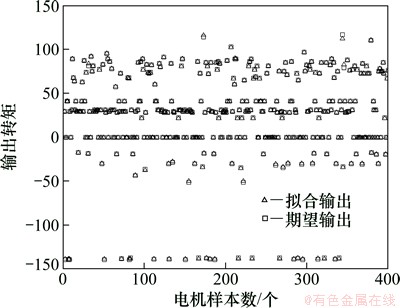
图12 CD模式下电机工作点的拟合精度
Fig. 12 Fitting accuracy of motor operating point in CD mode
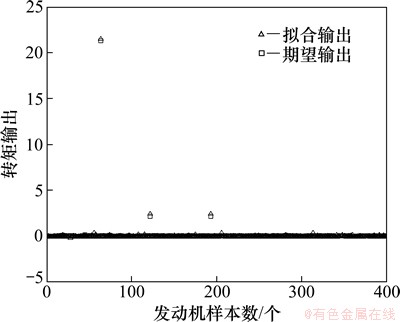
图13 CD模式下发动机工作点的拟合精度
Fig. 13 Fitting accuracy of engine operating point in CD mode
经过BP拟合得到电机与发动机的优化控制MAP图,如图16~19所示。根据行驶工况相应的驱动需求转矩和车速直接查表获得电机和发动机的扭矩输出量,从而实现控制策略的优化,其结果可用于车辆的实时控制。
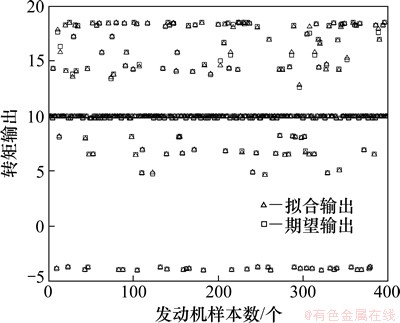
图14 CS模式下电机工作点的拟合精度
Fig. 14 Fitting accuracy of motor operating point in CS mode
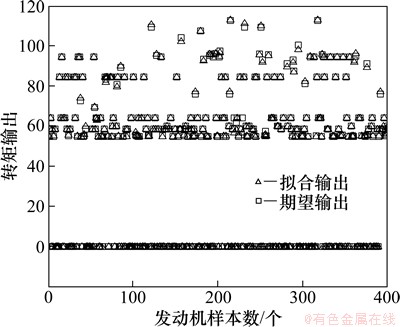
图15 CS模式下发动机工作点的拟合精度
Fig. 15 Fitting accuracy of engine operating point in CS mode
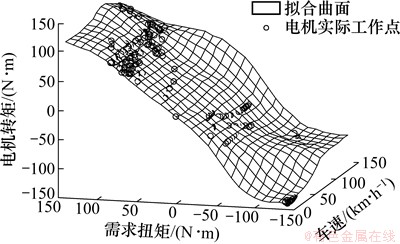
图16 CD模式下电机的工作曲面
Fig. 16 Working surfaces of motor in CD mode
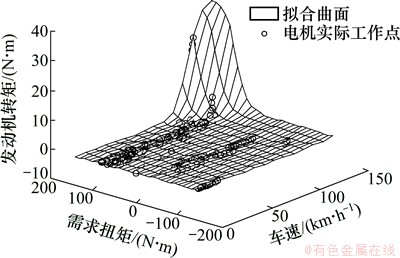
图17 CD模式下发动机的工作曲面
Fig. 17 Working surfaces of engine in CD mode
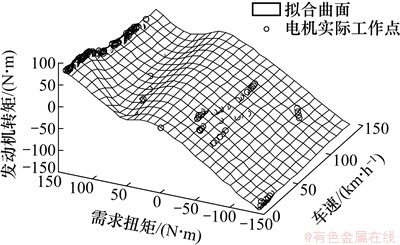
图18 CS模式下电机的工作曲面
Fig. 18 Working surfaces of motor in CS mode
4.2 BP控制策略的仿真结果
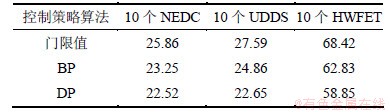
根据matlab/simulink仿真平台搭建仿真模型,分别对门限值控制策略[10-12] 和BP控制策略进行了仿真计算,仿真结果如表1所示。由表1可以看出:在NEDC、城市测功器驾驶进程(UDDS)和高速路燃油经济测试(HWFET)循环工况下,BP控制策略比DP算法的能耗经济性要差,但与门限值控制策略相比能耗经济性分别有10.09%,9.89%和8.17%的提高。
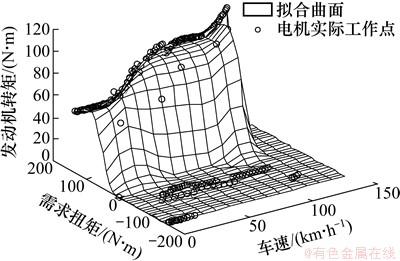
图19 CS模式下发动机的工作曲面
Fig. 19 Working surfaces of engine in CS mode
表1 不同工况的能耗经济性
Table 1 Energy consumption economy of different conditions 元
5 结论
1) 针对新型单电机PHEV,采用瞬时优化算法对CVT的速比进行实时优化,进而将该实时寻优结果嵌套在动态规划算法中,以CVT速比和电池SOC为状态变量,电机和发动机功率为控制变量,对循环工况进行全局寻优,得到电机和发动机间的功率分配。
2) 采用BP神经网络对发动机与电机的工作点进行训练拟合,得到电机与发动机的优化控制MAP图,用于车辆在循环工况的实时控制。
3) 在matlab/simulink的仿真平台上搭建模型进行仿真计算,结果表明BP控制策略与门限值控制策略相比,可使采用CVT的PHEV的能耗经济性在NEDC,UDDS和HWFET循环工况下分别有10.09%,9.89%和8.17%的提高。
参考文献:
[1] GENG Bo, James K, SUN Dong. Energy management control of micro turbine-powered plug-In hybrid electric vehicles using the telemetry equivalent consumption minimization strategy[J]. IEEE Transactions on Vehicular Technology, 2011, 60(9): 4238-4248.
[2] CHEN Zhang, Ardalan V. Route preview in energy management of plug-in hybrid vehicles[J]. IEEE Transactions on Control Systems Technology, 2012, 20(2): 546-553.
[3] YANG Bin, LI Yaoyu, GONG Qiuming, et al. Multi-information integrated trip specific optimal power management for plug-In hybrid electric vehicle[C]//American Control Conference. St Louis: ACC, 2009: 4607-4612.
[4] GONG Qiuming, LI Yaoyu, PENG Zhongren. Trip-based optimal power management of plug-In hybrid electric vehicle[J]. IEEE Transactions on Vehicular Technology, 2008, 57(6): 3393-3401.
[5] 张博, 郑贺悦, 王成. 可外接充电混合动力汽车能量管理策略[J]. 机械工程学报, 2011, 47(6): 113-119.
ZHANG Bo, ZHENG Heyue, WANG Cheng. Plug-in hybrid electric vehicle energy management strategy [J]. Journal of Mechanical Engineering, 2011. 47(6): 113-119.
[6] Moura S J, Duncan S, et al. Tradeoffs between battery energy capacity and stochastic optimal power management in plug-in hybrid electric vehicles[J]. Journal of Power Sources, 2010, 195: 2979-2988.
[7] Scott M, Hosam K, Duncan S, et al. A stochastic optimal control approach for power management in plug-In hybrid electric vehicles[J]. IEEE Transaction on Control Systems Technology, 2011, 19(3): 545-555.
[8] Mojtaba S Z, Abbas Z K, Steffen K, et al. Integrated thermal and energy management of plug-in hybrid electric vehicles[J]. Journal of Power Sources, 2012, 216: 237-248.
[9] 舒红, 聂天雄, 邓丽君, 等. 插电式混合动力汽车模型预测控制[J]. 重庆大学学报, 2011, 34(5): 36-41.
SHU Hong, NIE Tianxiong, DENG Lijun, et al. Model predictive control for a plug-in hybrid electric vehicle[J]. Journal of Chongqing University, 2011, 34(5): 36-41.
[10] Banvait H, Anwar S, CHEN Yaobin. A rule-based energy management strategy for plug_in hybrid electric vehicle (PHEV)[C]//American Control Conference. St Louis: ACC, 2009: 3938-3943.
[11] Fajri P, Asaei B. Plug-in hybrid conversion of a series hybrid electric vehicle and simulation comparison[C]//International Conference on Optimization of Electrical and Electronic Equipment. Brasov: OPTIM, 2008: 287-292.
[12] ZHANG Song, WU Guangqiang, ZHENG Songlin. Study on the energy management strategy of DCT-based series-parallel PHEV[C]//International Conference on Computing Control and Industrial Engineering. Wuhan: CCIE, 2010: 25-29.
(编辑 陈爱华)
收稿日期:2014-02-10;修回日期:2014-05-25
基金项目(Foundation item):国家科技支撑计划项目(2013BAG12B01);国家自然科学基金资助项目(51305468)(Project (2013BAG12B01) supported by National Key Technology Research and Development Program; Project (51305468) supported by the National Natural Science Foundation of China)
通信作者:杨官龙(1983-),男,山西闻喜人,博士研究生,从事混合动力控制策略研究;电话:13628498501;E-mail:yang67859755@163.com