DOI: 10.11817/j.ysxb.1004.0609.2020-35846

离子型稀土矿体的剪胀特性及其弹塑性本构模型的构建

洪本根¹，胡世丽²，罗嗣海²，王钰霖²，王观石²

(1. 江西理工大学 资源与环境工程学院，赣州 341000；

2. 江西理工大学 建筑与测绘工程学院，赣州 341000)

摘  要：通过塑性功增量分析离子型稀土矿体的剪胀特性，并在修正剑桥模型剪胀方程的基础上，提出离子型稀土矿体的剪胀方程，从而构建出适用于离子型稀土矿体的弹塑性本构模型。结果表明：1) 所构建新的剪胀方程能够较好地描述离子型稀土矿体的剪胀比和其应力比之间的关系；2) 确定了模型在一般应力状态下的弹塑性刚度矩阵，证明其对离子型稀土矿体的室内三轴CD试验结果具有较好的拟合效果，并进一步通过室内等p三轴试验和减p三轴试验验证了模型的有效性。

关键词：离子型稀土矿体；剪胀方程；弹塑性本构模型；三轴试验

文章编号：1004-0609(2020)-08-1957-10　　     中图分类号：TU41　　     文献标志码：A

目前，针对离子型稀土矿体的研究主要集中在其渗透特性^[1]、强度特性^[2-3]、矿体结构^[4]等方面，并以此为基础，进一步研究了矿山的单孔注液强度^[5]和临界注液范围^[6]。但未进行矿山的边坡变形分析，一般采用数值计算的方法^[7]，而弹塑性本构模型的设定决定了数值计算时边坡变形的结果，因此构建适用于离子型稀土矿山的弹塑性本构模型成为其边坡变形分析的关键问题。 对于不同的材料，由于其剪胀特性各不相同，因此，构建材料的弹塑性本构模型时，剪胀方程的构建成为核心问题。例如，张丙印等^[8]在分析堆石体三轴试验成果的基础上，提出修正Rowe剪胀方程，构建的本构方程能很好的反映堆石体的剪胀特性。王占军等^[9]同样以三轴试验成果为基础，考虑颗粒破碎引起堆石料剪胀比与应力比之间的非线性关系来构建剪胀方程，提出的本构模型能够反映堆石料低围压剪胀、高围压剪缩的特性。罗刚等^[10]通过将状态参数引入剪胀方程，建立了能够反映物态变化的砂土本构模型。姚仰平等^[11]在临界状态理论的基础上，通过引入状态参数来调整剪胀方程，构建的本构模型能较好地反映物态变化下砂土的剪胀、剪缩特性。 综上所述，本文以屏南某离子型稀土矿体为研究对象，以室内三轴试验成果为基础，分析了矿体的剪胀特性，并建立了能够描述其剪胀特性的剪胀方程，而后在此基础上推导出一般应力状态下的刚度矩阵，最终构建出该矿体的弹塑性本构模型。

1  离子型稀土矿体的剪胀特性

1.1  离子型稀土矿体的剪胀特性

近年来，针对土的剪胀特性已展开了大量的研究，并用剪胀方程加以描述。剪胀方程描述的是剪胀比与应力比之间的函数关系，剪胀比是指塑性体应变增量与塑性剪应变增量之比，应力比是指广义剪应力q与平均主应力p之比^[12]。 为建立能够描述离子型稀土矿体剪胀特性的剪胀方程，以屏南某离子型稀土矿体为研究对象，矿体的基本物理性质指标参数如表1所示，矿体的颗粒级配累计曲线如图1所示。根据表1中矿体的基本物理性质指标和图1中矿体的颗粒级配累计曲线判定该区域矿体为粉砂土。

表1  离子型稀土矿体的物理性质指标

Table 1  Physical property indexes of ion-absorbed rare earth ore body

图1  颗粒级配累计曲线

Fig. 1  Cumulative curve of grain composition

为得到矿体剪胀比与其应力比的关系曲线，开展了室内三轴CD试验。矿样密度为1.69 g/cm³，矿样质量含水率为18.27%，矿样直径50 mm，高度100 mm。采用反压饱和法对矿样进行饱和，之后在不同有效围压下对矿样进行固结；矿样固结完成后进行剪切试验，剪切速率为0.012 mm/min。为便于问题分析，现以有效围压100 kPa为例进行说明。根据有效围压100 kPa下的剪切数据，可得剪胀比与应力比的关系图，如图2所示，此处的剪胀比近似等于dε_v/dε_p。

图2  剪胀比与应力比的关系

Fig. 2  Relationship between dilatancy ratio and stress ratio

根据图2可知，随着应力比的增加，剪胀比逐渐减小。由文献可知，矿体变形的主要原因是施加的外力对矿体做功^[13]。根据文献可知^[12]，在力的作用下产生塑性变形所做的塑性功计算方法如式(1)所示：

                           (1)

式中：dW_p为塑性功增量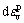；为塑性体积应变增量；为塑性剪应变增量。

由此，根据式(1)可分别计算出不同应力比条件下由塑性体积应变增量和塑性剪应变增量所引起的塑性功增量可分别用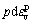和进行计算，计算结果如图3所示。由图3可知，随着应力比的增加，作用于塑性体积应变的塑性功增量逐渐减小，作用于塑性剪应变的塑性功增量逐渐增大，故塑性体积应变增量逐渐减小，塑性剪应变增量逐渐增大，即剪胀比逐渐减小。

图3  塑性功增量与应力比的关系

Fig. 3  Relationship between plastic work increment and stress ratio

1.2  修正剑桥模型剪胀方程适用性的讨论

由于修正剑桥模型的剪胀方程满足室内三轴CD试验的两个基本特点，即：临界破坏点q/p=M处，塑性体积应变为零，只有塑性剪应变；在q=0处，塑性剪应变为零，只有塑性体积应变，使其剪胀方程较为广泛的应用于描述土的剪胀特性^[14]。其中，修正剑桥模型的剪胀方程为：

                              (2)

式中：η为应力比，η=q/p；M为临界状态时的应力比。式(2)中，当应力比η小于M时，剪胀比大于零，表现为剪缩；当应力比η大于M时，剪胀比小于零，表现为剪胀。由此可见，修正剑桥模型的剪胀方程能够描述土的剪胀特性。

现以有效围压100 kPa的三轴CD试验数据为例，说明修正剑桥模型的剪胀方程对离子型稀土矿体的适用性。由修正剑桥模型的剪胀方程计算出100 kPa有效围压下剪胀比随应力比的变化规律，结合图2的室内试验结果，可得剪胀方程计算结果如图4所示。由图4可知，修正剑桥模型剪胀方程的计算结果与试验结果存在一定的误差，故给出两者的相对误差绝对值随应力比的变化规律，如图5所示。由图5可知，当应力比小于0.5时，两者的相对误差绝对值超过30%，当应力比大于0.5时，两者的相对误差绝对值大部分超过15%。故修正剑桥模型剪胀方程的计算结果与试验结果不一致。

图4  有效围压100kPa的剪胀方程计算结果

Fig. 4  Calculation results of dilatancy equation at effective confining pressure of 100 kPa

图5  相对误差绝对值随应力比的变化规律

Fig. 5  Relationship between absolute relative error and stress ratio

剪胀方程是描述岩土体力学行为的关键，而颗粒大小对颗粒材料的力学行为有显著影响^[15]。同时，修正剑桥模型适用于正常固结和轻微超固结黏土的弹塑性模型^[6]，且黏土颗粒粒径非常小，其粒径小于0.002 mm，孔径分布均匀，且一般情况下不会发生颗粒破碎，只有在极高压力作用下才可能发生颗粒破碎^[16]。故，本文从矿体孔径分布和颗粒大小的含量这两个方面来讨论修正剑桥模型剪胀方程计算结果与室内试验结果不一致的原因。 首先，分析矿体孔径分布是否均匀。采用筛分法和激光粒度分布仪测试方法分析矿体颗粒的相对含量，如表2所示。该矿体的黏粒含量仅有18.12%，与黏土相差较大。根据计算，离子型稀土矿体的不均匀系数C_u和曲率系数C_c分别为17.74和0.77，表明矿体为非均质土和级配不连续，故矿体内部孔隙分布不均匀。

表2  矿体颗粒的相对含量

Table 2  Relative content of ore particles

其次，通过对比试验前后矿体的颗粒级配曲线，即分析固结和剪切作用下矿体颗粒大小含量的变化。同理，采用筛分法和和激光粒度分布仪测试方法测试试验前后矿样的颗粒级配曲线，测试结果如图6所示。

图6  颗粒级配累计曲线

Fig. 6  Accumulative curves of grain gradation

由图6可知，矿样经过固结和剪切阶段，0.075~1 mm这一粒级范围内的颗粒破碎成更细小的粉粒和黏粒，其中粉粒含量增加11.64%，黏粒含量增加8.10%。

综合上述分析可知，离子型稀土矿体孔径分布不均匀，在固结和剪切作用下部分矿体颗粒会发生破碎。为进一步明确这两种情况对矿体剪应变增量和体应变增量的影响，现将试验所得体应变增量和剪应变增量与修正剑桥模型计算值进行对比，如图7和8所示。由图7和8可知，当应力比小于0.9时，体应变增量的试验值远大于模型计算值，剪应变增量的试验值与模型计算值接近；当应力比大于0.9时，体应变增量和剪应变增量的试验值与模型计算值均接近。由此可见，修正剑桥模型剪胀方程计算结果与室内试验结果不一致，即修正剑桥模型的剪胀方程不能直接用于描述离子型稀土矿体的剪胀特性。

图7  有效围压100 kPa下体应变增量与应力比的关系

Fig. 7  Relationship between volumetric strain increment and stress ratio at effective confining pressure of 100 kPa

图8  有效围压100 kPa下剪应变增量与应力比的关系

Fig. 8  Relationship between shear strain increment and stress ratio at effective confining pressure of 100 kPa

1.3  离子型稀土矿体剪胀方程的构建

鉴于修正剑桥模型的剪胀方程不能直接用于描述离子型稀土矿体的剪胀特性，故需构建新的剪胀方程。目前使用的剪胀方程大部分都是应用剑桥模型或者Rowe剪胀理论的剪胀方程及它们的改进型。如针对Rowe剪胀方程运用于堆石料，学者就先后提出三种改进方式，张丙印等^[8]通过对Rowe剪胀方程的主应力比与极限应力比的比值增加幂次项以修正Rowe剪胀方程；陈生水等^[17]通过引入剪胀应力比M_d以考虑颗粒破碎引起的堆石料剪胀比与应力比之间的关系，并将M_d作为修正系数，通过类比Rowe剪胀方程提出新的剪胀方程；王占军等^[9]在张丙印等^[8]和陈生水等^[11]所修正Rowe剪胀方程的基础上，通过引入因式exp(c/h)进一步修正了剪胀方程的曲线形态。 上述方法均是从试验结果拟合的角度对Rowe剪胀方程进行数学上的改进，只增加一个简单的拟合参数或者因式，为改进经典剪胀方程提供了可行的思路。但对离子型稀土矿体进行等向固结试验时，试验结果显示试样的塑性应变只有塑性体积应变增量，塑性剪应变增量为零，总塑性应变增量方向应平行于水平轴，而Rowe剪胀方程均不满足该条件，故仅对Rowe剪胀方程做数学上的改进并不能修正该缺陷。 对于修正剑桥模型剪胀方程，其满足等向固结试验时，试样的塑性应变只有塑性体积应变增量，塑性剪应变增量为零，但前文讨论了其不适用于离子型稀土矿体。由此，在修正剑桥模型剪胀方程的基础上，结合王占军等^[10]对Rowe剪胀方程的改进方法，提出离子型稀土矿体的剪胀方程，如式(3)所示。采用式(3)对试验曲线进行拟合，结果如图9所示，所得曲线与试验曲线的相关系数R²为0.97。

                  (3)

式中：M_d为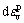等于零时所对应的应力比，该点表示的物理意义为矿体的体变由剪缩转向剪胀时的特征点；修正系数γ为拟合参数，100 kPa围压下取值1.85。

图9  有效围压100 kPa的剪胀方程拟合结果

Fig. 9  Fitting result of dilatancy equation at effective confining pressure of 100 kPa

为进一步验证所建立的离子型稀土矿体剪胀方程的适用性，采用式(3)描述有效围压分别为50 kPa和150 kPa的室内三轴CD试验所得到的剪胀比与应力比的关系，如图10所示，有效围压分别为50 kPa和150 kPa时，修正系数γ分别为1.84和1.83。

图10  不同有效围压下剪胀方程的拟合结果

Fig. 10  Fitting result of dilatancy equation at different effective confining pressures

2  离子型稀土矿体弹塑性本构模型的构建

当用p、q、ε_v、ε_d分别表示应力与应变及其增量，则应力应变增量关系式可简记如下：

                          (4)

由式(4)可知，当求得一般应力状态下弹塑性刚度矩阵[C^ep]时，即可得出由应变增量求应力增量的应力应变增量关系，二维弹塑性刚度矩阵的一般表达式：

                   (5)

式中：[C^e]为弹性刚度矩阵；H为塑性模量；n_g为塑性流动方向；n_f为加载方向。

2.1  塑性流动方向n_g和加载方向n_f

对于塑性流动方向n_g，由应力剪胀方程确定，本文已确定剪胀方程，由此确定塑性流动的方向矢量，即^[18]：

                     (6)

式中：d_g表示剪胀比，即d_g=/。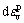

对于岩土材料，宜采用非关联的流动准则^[19]。为此，对于加载方向n_f，采用与塑性流动方向不同的加载方向向量，如式(7)所示。其中，d_f采用峰值应力比构造，根据LING的研究结论^[20-21]，d_f的表达式与d_g类似，如式(8)所示。

                     (7)

                    (8)

式中：M_f为峰值应力比。

2.2  塑性模量H

由式(5)可知，在确定弹塑性刚度矩阵时，还需要确定塑性模量H。 首先从等向压缩试验条件出发，即q=dq=0，h=0时，塑性模量H可表示为：

                                (9)

式中：e₀为初始孔隙比；l为正常圧缩线斜率；k为弹性回弹线斜率。

根据图4可知，矿样经过固结和剪切这两个阶段后，0.075~1 mm这一粒级范围内的颗粒破碎成更细小的粉粒和黏粒，故在加载压缩时，压缩曲线发生下弯。因此，对于e和p的关系，本文采用如下指数函数^[22]：

                         (10)

由于l为等向压缩时e-曲线的斜率，即根据式(10)将e对求导数即可得到l与e和p的关系为：

                              (11)

式中：h_s为矿体的固相硬度，为应力的量纲；n为无量纲的材料参数；两者通过等向压缩试验确定。

对于室内三轴CD试验，塑性模量H随着加载剪切的进行是逐渐减小直至为零。由此，参照文献[9]、[17]和[23]，经过大量试算后，塑性模量H可采用下式进行计算：

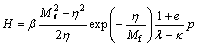             (12)

由此，将式(6)、式(7)和式(12)代入式(5)可得一般应力状态下的弹塑性刚度矩阵，之后将式(5)代入式(4)可得矿体的弹塑性本构模型。

3  模型参数的确定及模型的验证

3.1  模型参数的确定方法

模型中的应变一般有弹性应变和塑性应变两个部分组成，故模型参数的确定需分成两个部分进行考虑。

3.1.1  弹性应变部分

就弹性应变部分而言，由广义胡克定律确定，参数有泊松比和弹性模量E。对于离子型稀土矿体，其泊松比的取值与其土性有关。由于该离子型稀土矿体为粉砂土，由此其泊松比的取值为0.35^[24]。 对于离子型稀土矿体的弹性模量E，其会随着应力状态的变化而变化，本文采用式(13)进行计算^[17]：

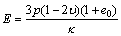                        (13)

3.1.2  塑性应变部分

就塑性应变部分而言，根据式(3)、(8)、(11)和(12)，参数有峰值应力比M_f、塑性体积应变增量为零时的应力比M_d、修正系数γ、矿体的固相硬度h_s、材料参数n、弹性回弹线斜率和调节系数β。 M_f的确定方法如下：开展有效围压分别为50、100和150 kPa的室内三轴CD试验，在三种有效围压下离子型稀土矿体的应力应变曲线均为应变硬化型，取轴向应变的15%所对应的应力比作为峰值应力比^[23]，故可得有效围压为50、100和150 kPa下的峰值应力比分别为1.43、1.39和1.37。根据文献[19]，不同有效围压下的峰值应力比M_f可采用式(14)进行计算。通过数据拟合，得到M_f0为1.62，△M_f为0.11，如图11所示。

                        (14)

式中：M_f0和△M_f通过拟合M_f和得到。

M_d的确定方法如下：开展有效围压分别为50、100和150 kPa的室内三轴CD试验，在三种有效围压下离子型稀土矿体的体应变先增大后保持不变，故可得有效围压为50、100和150 kPa下且体应变增量为零时的应力比分别为1.48、1.43和1.40。同理，可采用式(15)计算不同有效围压下的M_d。通过数据拟合，得到M_d0为1.72，△M_d为0.14，如图12所示。

                        (15)

式中：M_d0和△M_d通过拟合M_d和得到。

图11  M_f和的关系

Fig. 11  Relationship between M_f and

图12  M_d和的关系

Fig. 12  Relationship between M_d and

γ的确定方法如下：利用剪胀方程式(2)拟合剪胀比和应力比的关系曲线，取各围压下的平均值，即γ为1.84。 h_s和n的确定方法如下：进行各向等压固结排水试验^[25]，采用反压饱和矿样结束后，依次增加有效围压至20、50、100、150和200 kPa时固结，每级加载均待试样完成固结后再进行下一步加载；由此画出e-p曲线，根据式(11)对试验曲线进行回归分析，如图13所示。根据回归分析结果，h_s为870 kPa，n为1.28。 的确定方法如下：进行各向等压固结排水试验^[25]，增加有效围压至200 kPa时固结；待固结完成后将有效围压依次卸载至200、150、100和50 kPa，每级卸载均待矿样自由膨胀稳定后再进行下一步卸载；由此可同样画出e-曲线，根据曲线的斜率确定，如图14所示。由图14可知，随着的减小，孔隙比呈现线性增大的趋势，采用线性方程对试验数据进行拟合可得e=0.86-0.0063，由此可得弹性回弹线斜率=0.0063。

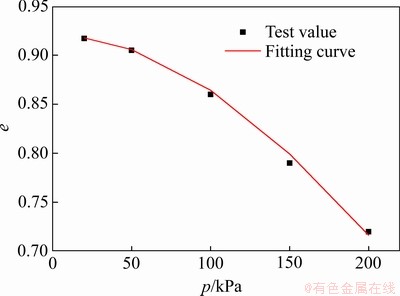
图13  参数l的求解图

Fig. 13  Solution diagram of parameter l

图14  参数的求解图

Fig. 14  Solution diagram of parameter

β的确定方法如下：通过最小二乘法拟合室内三轴CD试验所得的应力应变曲线确定。

3.2  模型的验证

首先，通过已构建的本构模型，采用最小二乘法拟合有效围压50、100和150 kPa下轴向应变和体应变的关系，如图15和16所示。由图15和16可知，所建模型对各围压下轴向应变和体应变的关系以及轴向应变和偏应力的关系具有较好的拟合效果，由此确定调节系数β的值为0.43。 为进一步验证模型的适用性，开展两组室内三轴试验，一组为等p三轴试验，即增大轴向压力s₁，减小围压s₃，保持平均正应力p不变，试验时设定初始的p分别为100 kPa和150 kPa；另一组为减p三轴试验，即保持s₁不变，减小s₃，从而p减小，试验时设定初始的p分别为100 kPa和150 kPa。然后，利用构建的模型计算出这两种情况下的轴向应变和体应变的关系以及轴向应变和偏应力的关系，并与试验值作对比，以此来说明模型的有效性。模型计算时，各参数取值如表3所示。

图15  CD试验的体应变与轴向应变的关系

Fig. 15  Relationship between volumetric strain and axial strain of CD test

图16  CD试验的偏应力与轴向应变的关系

Fig. 16  Relationship between deviatoric stress and axial strain of CD test

表3  矿体的本构模型参数

Table 3  Constitutive model parameters of orebody

等p应力路径条件下，模型计算值和试验值如图17和18所示。由图17和18可知，初始平均正应力p分别为100 kPa和150 kPa的条件下，模型计算的轴向应变和体应变的关系以及轴向应变和偏应力的关系与试验值吻合较好。 同理，减p应力路径条件下，模型计算值和试验值如图19和20所示。由图19和20可知，初始平均正应力p分别为100 kPa和150 kPa的条件下，模型计算的轴向应变和体应变的关系以及轴向应变和偏应力的关系与试验值吻合较好。

图17  等p试验的体应变与轴向应变的关系

Fig. 17  Relationship between volumetric strain and axial strain of constant p test

图18  等p试验的偏应力与轴向应变的关系

Fig. 18  Relationship between partial stress and axial strain of constant p test

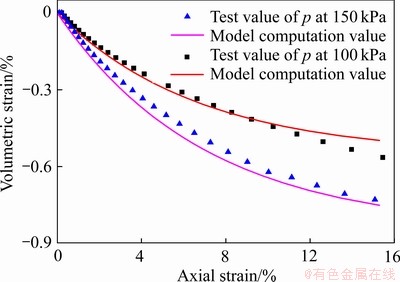
图19  减p试验的体应变与轴向应变的关系

Fig. 19  Relationship between volumetric strain and axial strain of decreased p test

图20  减p试验的偏应力与轴向应变的关系

Fig. 20  Relationship between partial stress and axial strain of decreased p test

综合上述，在等p和减p应力路径条件下，模型计算值与试验值均吻合较好，由此说明了所建立的模型是有效的。

4  结论

1) 在修正剑桥模型剪胀方程的基础上进行了改进，得到新的剪胀方程，该剪胀方程能够较好的描述离子型稀土矿体的剪胀比与其应力比之间的关系。 2) 构建的离子型稀土矿体的广义弹塑性本构模型对离子型稀土矿体的室内三轴CD试验结果具有较好的拟合效果，并进一步通过室内等p三轴试验和减p三轴试验验证了该本构模型的有效性。

REFERENCES

[1] 周贺鹏, 胡 洁, 罗仙平, 钟志刚. 离子型稀土矿渗流溶浸行为研究[J]. 稀有金属, 2018, 42(5): 531-536.

ZHOU He-peng, HU Jie, LUO Xian-ping, ZHONG zhi-gang. Percolation leaching behavior of ion-adsorption-type rare earth ore[J]. Chinese Journal of Rare Metals, 2018, 42(5): 531-536.

[2] 王洪丁, 王观石, 邱高磊, 罗嗣海. 离子型稀土矿体强度特性试验研究[J]. 中国矿业, 2016, 25(9): 136-140, 147.

WANG Hong-ding, WANG Guan-shi, QIU Gao-lei, LUO Si-hai. Research into strength characteristics for ion-adsorption rare earth ore[J]. China Mining Magazine, 2016, 25(9): 136-140, 147.

[3] 尹升华, 齐 炎, 谢芳芳, 陈 勋, 王雷鸣. 不同孔隙比下风化壳淋积型稀土矿强度特性[J]. 工程科学学报, 2018, 40(2): 159-166.

YIN Sheng-hua, QI Yan, XIE Fang-fang, CHEN Xun, WANG Lei-ming. Strength characteristics of weathered crust elution-deposited rare earth ores with different porosity ratios[J]. Chinese Journal of Engineering, 2018, 40(2): 159-166.

[4] 王观石, 王小玲, 胡世丽, 洪本根. 颗粒运移对离子型稀土矿体结构影响的试验研究[J]. 矿业研究与开发, 2015, 35(10): 37-42.

WANG Guan-shi, WANG Xiao-ling, HU Shi-li, HONG Ben-gen. Experimental study on the effect of particle migration on the structure of ionic rare earth ore body[J]. Mining R&D, 2015, 35(10): 37-42.

[5] 桂 勇, 王观石, 赖远明, 洪本根, 胡世丽, 龙 平. 原地浸矿单孔注液影响半径的计算模型[J]. 中国有色金属学报, 2018, 28(5): 1050-1058.

GUI Yong, WANGGuan-shi, LAIYuan-ming, HONG Ben-gen, HU Shi-li, LONG ping. A calculation model of influence radius of single-hole injection in in-situ leaching[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(5): 1050-1058.

[6] 洪本根, 罗嗣海, 胡世丽, 王观石. 全覆式离子型稀土矿山临界注液范围的计算[J]. 中国有色金属学报, 2019, 29(7): 1509-1518.

HONG Ben-gen, LUO Si-hai, HU Shi-li, WANG Guan-shi. Calculation of critical liquid injection range in full clad ion-absorbed rare earth mine[J]. The Chinese Journal of Nonferrous Metal, 2019, 29(7): 1509-1518.

[7] SONG Fei, CHAI Hai-bo, MA Li-qiu, HU Hong-bing. Numerical analysis on deformation behavior of geosynthetic-reinforced slopes[J]. Revista de la Facultad de Ingenieria, 2016, 31(3): 40-48.

[8] 张丙印, 贾延安, 张宗亮. 堆石体修正Rowe剪胀方程与南水模型[J]. 岩土工程学报, 2007, 29(10): 1443-1448.

ZHANG Bing-yin, JIA Yan-an, ZHANG Zong-liang. Modified Rowe’s dilatancy law of rockfill and Shen Zhujiang’s double yield surfaces elastoplastic model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10): 1443-1448.

[9] 王占军, 陈生水, 傅中志. 堆石料的剪胀特性与广义塑性本构模型[J]. 岩土力学, 2015, 36(7): 1931-1938.

WANG Zhan-jun, CHEN Sheng-shui, FU Zhong-zhi. Dilatancy behaviors and generalized plasticity constitutive model of rockfill materials [J]. Rock and Soil Mechanics, 2015, 36(7): 1931-1938.

[10] 罗 刚, 张建民. 考虑物理状态变化的砂土本构模型[J]. 水利学报, 2004, 35(7): 26-31.

LUO Gang, ZHANG Jian-min. Constitutive model for sand considering the variation of its physical state[J]. Journal of Hydraulic Engineering, 2004, 35(7): 26-31.

[11] 姚仰平, 余亚妮. 基于统一硬化参数的砂土临界状态本构模型[J]. 岩土工程学报, 2011, 33(12): 1827-1832.

YAO Yang-ping, YU Ya-ni. Extended critical state constitutive model for sand based on unified hardening parameter[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1827-1832.

[12] 罗 汀, 姚仰平, 侯 伟. 土的本构关系[M]. 北京:人民交通出版社, 2010.

LUO Ting, YAO Yang-ping, HOU Wei. Soil constitutive relationship[M]. Beijing: China Communications Press, 2010.

[13] 阮红风, 罗 强, 孟伟超, 蒋良潍, 张 良. 基于直剪试验的土体变形时间效应及状态类别分析[J]. 岩土力学, 2016, 37(2): 453-464.

RUAN Hong-feng, LUO Qiang, MENG Wei-chao, JIANG Liang-wei, ZHANG Liang. Analysis of time-effect characteristics of soil deformation and its classification based on direct shear test[J]. Rock and Soil Mechanics, 2016, 37(2): 453-464.

[14] 李顺群, 张建伟, 夏锦红. 原状土的剑桥模型和修正剑桥模型[J]. 岩土力学, 2015, 36(S2): 215-220.

LI Shun-qun, ZHANG Jian-wei, XIA Jin-hong. An improvement on Cam-clay model and modified Cam-clay model for intact soil[J]. Rock and Soil Mechanics, 2015, 36(S2): 215-220.

[15] 戴北冰, 杨 峻, 周翠英. 颗粒大小对颗粒材料力学行为影响初探[J]. 岩土力学, 2014, 35(7): 1878-1884.

DAI Bei-bing, YANG Jun, ZHOU Cui-ying. A preliminary investigation on effect of particle size on mechanical behavior of granular materials[J]. Rock and Soil Mechanics, 2014, 35(7): 1878-1884.

[16] 王乃东, 姚仰平. 粒状材料颗粒破碎的力学特性描述[J]. 工业建筑, 2008(8): 17-20.

WANG Nai-dong, YAO Yang-ping. Mechanical description for granular material exhibiting particle crushing[J]. Industrial Architecture, 2008(8): 17-20.

[17] 陈生水, 傅中志, 韩华强, 彭 成. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489-1495.

CHEN Sheng-shui, FU Zhong-zhi, HAN Hua-qiang, PENG Cheng. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489-1495.

[18] PASTOR M, ZIENKIEWICZ O C, CHAN A H C. Generalized plasticity and the modelling of soil behavior[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1990, 14(3): 151-190.

[19] 殷宗泽. 土工原理[M]. 北京:中国水利水电出版社, 2007.

YIN Zong-ze. Geotechnical principle[M]. Beijing: China Water Conservancy and Hydropower Press, 2007.

[20] LING H I, YANG S T. Unified sand model based on the critical state and generalized plasticity[J]. Journal of Engineering Mechanics, 2006, 132(2): 1380-1391.

[21] LING H I, LIU H B. Pressure-level dependency and densification behaviour of sand through generalized plasticity model[J]. Journal of Engineering Mechanics, 2003, 129(8): 851-860.

[22] GUDEHUS G. A comprehensive constitutive equation for granular materials[J]. Soils and Foundations, 1996, 36(1): 1-12.

[23] 郭万里, 朱俊高, 彭文明. 粗粒土的剪胀方程及广义塑性本构模型研究[J]. 岩土工程学报, 2018, 40(6): 1103-1110.

GUO Wan-li, ZHU Jun-gao, PENG Wen-ming. Study on dilatancy equation and generalized plastic constitutive model for coarse-grained soil[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1103-1110.

[24] 张克恭, 刘松玉. 土力学[M]. 第三版. 北京:中国建筑工业出版社, 2010.

ZHANG Ke-gong, LIU Song-yu. Soil mechanics [M]. 3rd ed. Beijing: China Construction Industry Press, 2010.

[25] 周葆春, 王靖涛, 杨晓东. 武汉粘土修正剑桥模型参数研究[J]. 武汉理工大学学报, 2007, 29(3): 103-107.

ZHOU Bao-chun, WANG Jing-tao, YANG Xiao-dong. Research on parameters of modified cam clay for Wuhan clay[J]. Journal of Wuhan University of Technology, 2007, 29(3): 103-107.

Dilatancy behaviors and construction of elastoplastic constitutive model of ion-absorbed rare earth orebody

HONG Ben-gen¹, HU Shi-li², LUO Si-hai², WANG Yu-lin², WANG Guan-shi²

(1. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;

2. School of Architectural and Surveying& Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)

Abstract: The dilatancy behaviors of ion-absorbed rare earth ore body were analyzed by the increment of plastic deformation work. On the basis of the dilatancy equation of the modified Cambridge model, the dilatancy equation suitabled for ion-absorbed rare earth ore body was proposed, then a new elastoplastic constitutive model was proposed. The results show the main conclusions are as follows: 1) The new dilatancy equation can well describe the relationship between dilatancy ratio and stress ratio of ion-absorbed rare earth ore body; 2) The elastoplastic stiffness matrix of the model under the general stress state is deduced, the model has made considerable fitting results for the triaxial CD test results, and the triaxial constant p test and the triaxial decreased p test verify its effectiveness.

Key words: ion-absorbed rare earth ore body; dilatancy equation; elastoplastic constitutive model; triaxial test

Foundation item: Projects(41602311, 51664015) supported by the National Natural Science Foundation of China; Project(YB2017003) supported by the Jiangxi University of Science and Technology Excellent Doctoral Dissertation Nurturing Project, China; Project(20192BAB206048) supported by the Natural Science Foundation of Jiangxi Province, China; Project(JXUSTQJBJ2016007) supported by the Qingjiang Young Talents Support Program of Jiangxi University of Technology, China

Received date: 2019-08-21; Accepted date: 2019-12-28

Corresponding author: HU Shi-li; Tel: +86-13576686778; E-mail: hslqhd@ 163.com

(编辑  何学锋)

基金项目：国家自然科学基金资助项目(41602311，51664015)；江西省自然科学基金项目(20192BAB206048)；江西理工大学清江青年英才支持计划资助项目(JXUSTQJBJ2016007)；江西理工大学优秀博士学位论文培育项目(YB2017003)

收稿日期：2019-08-21；修订日期：2019-12-28

通信作者：胡世丽，副教授，博士；电话：13576686778；E-mail：hslqhd@163.com