DOI： 10.11817/j.issn.1672-7207.2020.01.024

斜拉索损伤对在役斜拉桥体系可靠度的影响

颜东煌¹,郭鑫^{1, 2}

（1. 长沙理工大学 土木工程学院，湖南 长沙，410114；

2. 长沙理工大学 长沙理工大公路工程试验检测中心，湖南 长沙，410007）

摘要:为了研究拉索腐蚀与疲劳损伤对在役斜拉桥服役安全的影响，分析平行钢丝拉索斜拉桥的时变体系可靠度。采用串-并联模型研究平行钢丝索强度概率受拉索长度和数量的影响，对比拉索断裂产生的静力与动力效应，并基于更新响应面方法捕捉拉索断裂产生的非线性效应。基于钢丝的疲劳试验结果评估某双塔混凝土斜拉桥的时变体系可靠度。研究结果表明：腐蚀和未腐蚀拉索20 a的抗拉强度均值分别下降32%和13%，基于串-并联模型可捕捉钢丝长度和数量效应对拉索强度概率分布均值和标准差的影响；单根拉索断裂可导致相邻拉索索力静力效应增加7%，而动力效应达到11%；基于更新响应面方法采用20个均匀设计样本点即可捕捉到该非线性效应；在“疲劳”和“腐蚀-疲劳”这2种损伤作用下，该斜拉桥在第20年的结构体系可靠指标由4.62分别下降至4.42和和2.46，表明腐蚀效应对斜拉桥运营期体系可靠度影响显著。

关键词:斜拉桥；斜拉索；体系可靠度；腐蚀；损伤

中图分类号:U441⁺.4;U448.25          文献标志码:A

文章编号:1672-7207（2020）01-0213-08

Influence of damage of stay cables on system reliability of in-service cable-stayed bridges

YAN　Donghuang¹, GUO　Xin^{1, 2}

(1. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China；

2. Institute of Highway Detection, Changsha University of Science & Technology, Changsha 410007, China)

Abstract: In order to study the influence of cable corrosion and fatigue damage on the service safety of in-service cable-stayed bridges, the reliability index of time-varying system of parallel steel cable cable-stayed bridges was analyzed. The series-parallel model was used to study the influence of the characteristic parameters of the parallel cable strength probability on the length and quantity of the cable. The static and dynamic effects generated by the cable break were compared, and the non-resistance response surface method was used to capture the nonlinear of the cable break. Based on the fatigue test results of steel wire, the reliability of time-varying system of a double-tower concrete cable-stayed bridge was evaluated. The results show that the average tensile strength of corrosion and uncorroded cables decreases by 32% and 13% after 20 a, respectively. Based on the series-parallel model, the length and quantity effects of the steel wire can be captured for the mean and standard deviation of the cable strength probability distribution. Single cable breaks can cause the static force effect of adjacent cables to increase by 7%, while the dynamic effect reaches 11%. This nonlinear effect can be captured by using 20 uniform design sample points based on the updated response surface method. With the two damages of fatigue and corrosion-fatigue, the reliability index of the cable-stayed bridge in the 20th year decreases from 4.62 to 4.42 and 2.46, respectively. This phenomenon indicates the significant effect of corrosion on the reliability of the cable-stayed bridge during the operation period.

Key words: cable-stayed bridge; stay cable; system reliability; corrosion; damage

斜拉桥具有跨越能力大、经济性能好、外观优美等优点，是中大跨度桥梁的首选桥型。我国建设了一大批混凝土斜拉桥，主跨最大达1 088 m。然而，在役斜拉桥运营期间出现了一系列耐久性问题，如拉索腐蚀、锚头锈蚀、索力损失等。其中，由于拉索腐蚀导致的拉索寿命较低的现象是威胁斜拉桥运营安全的主要问题，且拉索全部更换的造价往往达到施工成本的5倍以上，甚至超出全桥造价。准确评估斜拉索腐蚀情况下斜拉桥结构体系的安全性，为拉索更换提供理论基础。许多研究者通过斜拉索腐蚀疲劳试验研究了拉索腐蚀后的力学性能^[1]、疲劳强度^[2]和剩余寿命^[3]。在斜拉索腐蚀后的抗力概率模型方面，FABER等^[4]在平行钢丝腐蚀疲劳试验的基础上，研究了拉索的剩余承载力与强度概率模型，认为腐蚀疲劳复合因素作用下钢丝数量与长度效应对拉索强度均值的影响分别达10%和8%。LAN等^[5-6]采用Monte Carlo抽样方法对斜拉索疲劳寿命概率特征进行研究，发现斜拉索的疲劳寿命由短索的断裂控制。兰成明等^[7]采用PSN曲线和等效损伤路径方法研究了斜拉索疲劳寿命的概率分布函数，认为钢丝数量增加会减小其疲劳寿命的变异性，而疲劳寿命均值基本不受影响。由于斜拉桥是超静定结构体系，单根拉索的断裂并不致使桥梁倒塌，因此，人们对斜拉索腐蚀后斜拉桥的安全问题进行了研究。LI等^[8]研究了高强钢丝腐蚀疲劳对斜拉桥剩余承载力的影响，据此评估了南京长江三桥的承载力。刘沐宇等^[9]研究了斜拉索疲劳损伤对斜拉桥可靠度的影响。鲁乃唯等^[10]采用联合智能算法分析了斜拉桥运营期的主要失效路径，认为首要失效路径是边跨拉索断裂导致索塔弯曲破坏，其次是中跨拉索断裂导致跨中主梁破坏。LU等^[11]提出了基于支持向量回归的斜拉桥时变体系可靠度分析方法。然而，斜拉索的腐蚀疲劳损伤对斜拉桥体系可靠度影响机理尚未明确，为此，本文作者对在役斜拉桥的斜拉索腐蚀疲劳损伤对其体系可靠度的影响进行研究。首先，建立腐蚀拉索疲劳损伤后的剩余强度概率模型；其次，提出一种能够捕捉拉索强度退化对斜拉桥体系失效路径影响的高效分析方法；最后，以某双塔混凝土斜拉桥为例，分析斜拉索腐蚀对其体系可靠度的影响规律。研究结果可为在役斜拉桥的安全评定与换索决策提供依据。

1 平行钢丝索的静力强度

斜拉索的静力强度模型需要考虑2方面的因素^[12]：首先是单根细长钢丝的多点坑蚀导致的材料强度下降问题即长度效应问题；其次是平行钢丝数量增加导致其强度下降的因素（即丹尼尔效应问题）。

1.1　单根钢丝的静力强度

将单根钢丝沿其长度方向划分为若干个单元，则该钢丝的强度与单元的数量和钢丝的长度有关，形成一个串联系统。显然，单根钢丝的强度由其最薄弱的节段所决定。

钢丝材料的缺陷或者腐蚀等因素引起的损伤对钢丝静力强度的影响均可通过相关系数ρ表示(0<ρ<1)。ρ接近于1表示钢丝缺陷较少，ρ接近于0表示钢丝缺陷较多。引入相关长度参数L_ρ，L_ρ=lL₀(其中，L₀为试验样本钢丝的长度；l为系数，l大于1表示相关长度大于试验样本长度，即串-并联模型中的单元数量可减小；l小于1表示相关长度大于试验样本长度，即串-并联模型的单元数量应增加)。

假定某钢丝可划分为m个单元，且单元之间具有一定的相关性，则钢丝的强度可表示为

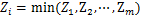(1)

式中：Z_i为第i个单元的强度。FABER等^[4]进行钢丝静力试验时发现钢丝强度服从Weibull分布：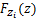

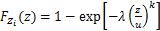(2)

式中：z为斜拉索的强度；λ，u和k分别为Weibull分布函数的尺度、位置和形状参数。上述参数可采用钢丝样本的静力强度试验结果，由最大似然估计方法得出近似解。

1.2　平行钢丝索的静力强度

当斜拉索钢丝的数量足够大时，平行钢丝索的强度服从正态分布，拉索强度均值可表示为

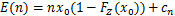(3)

式中：n为钢丝数量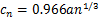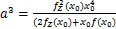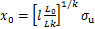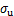；；；；为均斜拉索钢丝的极限强度；L为拉索总长。相应地，标准差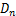可表示为

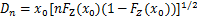(4)

式中：c_n为由于拉索数量引起的附加相关项，当n大于150时，该数值可忽略；而当n小于150时，c_n可表示为数量效应的修正系数^[13]。

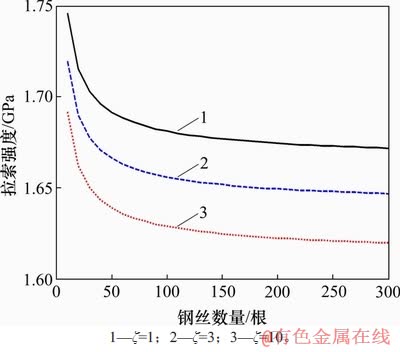
图1　钢丝数量对斜拉索强度的影响

Fig. 1　Influence of number of wire on cable-stay strength

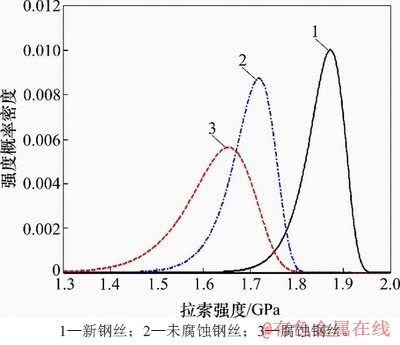
图2　短钢丝样本的试验强度概率密度曲线

Fig. 2　Probability density curves of tested strength of short cable specimem

需说明的是：斜拉索损伤的量化与其损伤程度有较大关系，拉索运营期腐蚀损伤程度有多种划分方法^[14]，JTG/T-H21—2011“公路桥梁技术状况评定标准”给出了5个等级的钢丝分级及描述。为了研究腐蚀对斜拉索强度退化概率的影响，本文采用前4个损伤等级，即钢丝状态处于“完好”至“密集蚀坑”之间。

1.3　算例分析

假定拉索钢丝样本数量为30个^[4]，样本极限强度均值σ_u=1 788.7 MPa，Weibull模型的分布参数k=72.62，假定比例因子ξ(即L/L₀)分别为1，3和10，则拉索钢丝数量从10根变化至300根的斜拉索强度退化模型如图1所示。

由图1可知：斜拉索强度随着钢丝数量增加有所下降，且随着比例因子ξ增加而下降；当ξ=10时，钢丝数量由10根增加至300根导致斜拉索强度下降4.3%。在1根斜拉索的钢丝数量为300根的情况下，比例因子ξ由1提高至10将导致斜拉索强度下降约3%。

LI 等^[15]对运营20 a的69根腐蚀平行钢丝索与13根未腐蚀平行钢丝索进行疲劳试验研究，采用样本长度l₀=0.5 m的钢丝，钢丝样本的强度概率密度曲线如图2所示。基于文献[4]中的钢丝样本的强度概率模型，考虑长度为232 m、数量n=243根的某实桥斜拉索。该斜拉索设计强度σ_b=1 766 MPa，则由式(3)和式(4)可得到该斜拉索的强度退化概率模型如图3所示。

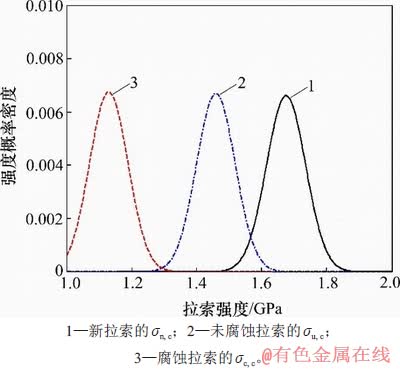
图3　斜拉索的强度概率模型

Fig. 3　Probabilistic model of cable strength

图3中，σ_{c, c}，σ_{u, c}和σ_{n, c}分别表示腐蚀拉索、未腐蚀拉索和新索的抗拉强度。拉索运营20 a后，腐蚀拉索和未腐蚀拉索的强度相对新拉索分别下降32%和13%，而标准差下降幅度不到2%。由此可知，拉索数量和长度效应导致的拉索强度变异系数相对于均值而言可忽略不计。

2 斜拉桥时变失效路径搜索方法

2.1　斜拉桥结构体系特征

斜拉桥是由斜拉索、主梁、索塔等多个构件组成的超静定结构体系。斜拉桥的体系失效是一连串构件失效所致，因此，关键失效路径的各单元强度退化将改变失效路径。

考虑斜拉索强度时变特性导致的结构体系时变失效路径搜索的关键点如下^[16]。

1) 斜拉桥结构体系的非线性行为。斜拉索的垂度效应与梁柱效应具有非线性行为，斜拉索不仅强度退化，而且其弹性模量也将发生改变。采用非线性功能函数捕捉结构的非线性行为将影响计算精度与效率。

2) 一种搜索斜拉桥结构体系主要失效路径的高效方法。斜拉桥结构超静定次数较多，失效路径多，关键失效路径是影响效应效率的关键所在。

3) 如何考虑斜拉索的时变抗力退化参数对斜拉桥结构体系时变可靠度的影响，识别拉索强度退化如何导致结构体系失效路径转移。

2.2　基于更新响应面的失效路径搜索方法

针对上述关键点，本文基于文献[17]所提出的更新支持向量方法，采用一种更新响应面方法与β约界法相结合的实用分析方法，用于搜索斜拉桥时变体系的失效路径。相对于更新支持向量方法而言，本文所提出的更新响应面方法更加简单、明确，但对线性的捕捉精度可能比更新支持方向方法的低。该方法的分析流程如图4所示，其中，T和T_s分别表示当前步骤计算时间和桥梁设计寿命。

图4所示流程图的关键步骤如下：

1) 通过结构的参数敏感分析，筛选影响结构主要失效模式的关键随机变量，如荷载、拉索弹模、混凝土容重等。

2) 采用二次序列响应面方法拟合随机变量与桥梁关键构件响应之间的函数关系，由Monte Carlo抽样方法计算各关键构件的可靠指标。

3) 采用β约界方法搜索关键构件的失效单元，并对失效单元进行处理。若构件发生脆性破坏，则删除失效单元；若构件发生塑性破坏，则增加塑性铰。

4) 基于斜拉桥新结构更新响应面，重复步骤2)和3)，直至结构体系失效，再构建结构的失效树。

5) 考虑斜拉索腐蚀导致的抗力退化概率模型，更新斜拉索参数，返回步骤1)。

6) 计算时间达到斜拉索设计年限(20～30 a)时结束。

采用如图4所示的更新响应面方法分析斜拉桥体系可靠度的优势在于：

1) 采用二次序列响应面函数来拟合斜拉桥构件的荷载效应，可捕捉其一定程度的非线性效应，如拉索垂度效应、梁柱效应及大变形等，详细内容见文献[18]。

2) 采用β约界方法搜索潜在失效单元，并以更新响应面的方法拟合单元失效后的新结构功能函数，捕捉到单元失效后结构体系的特性。

3) 考虑斜拉索抗力退化，再次更新斜拉桥有限元模型，重新对失效构件进行筛选分析。虽然计算较繁琐，但可捕捉斜拉索抗力退化对结构体系可靠度的影响。

3 双塔混凝土斜拉桥可靠度研究

3.1　工程背景

某斜拉桥的跨径为(210+420+210) m，结构体系为刚构体系，双塔混凝土π型主梁结构^[18]。主梁为C60混凝土材料，主塔为C50混凝土材料，斜拉索为钢绞线。主梁与斜拉索均为34对，桥面宽度为30 m，双向6车道，按照公路-I级汽车荷载设计。桥梁的结构尺寸如图5所示。图5中：C_m¹~C_m³⁴为中跨第1至第34号拉索，C_s¹～C_s³⁴为边中第1号至第34号拉索，G_s¹～G_s³⁴表示边跨第1号至第34号主梁，G_m¹～G_m³⁴表示中跨第1号至第34号主梁；P₁与P₂为索塔的弯曲失效控制点，P₃为主梁弯曲失效控制点。

3.2　确定性结构分析

采用有限元软件ANSYS建立桥梁的有限元模型，如图6所示，其中，斜拉索采用LINK180 单元，主梁与索塔均采用BEAM188单元。考虑最不利车辆荷载以均布荷载的形式加载至桥梁。根据文献[18]中分析结果，斜拉桥最易失效的拉索是最长索。文献[19]的研究结果表明锈蚀断丝对斜拉索的力学性能有较大影响。针对本斜拉桥，选取中跨34号拉索为例，分析该斜拉索断裂之后相邻拉索33，32和31号拉索索力及主梁与索塔关键截面弯矩的变化。

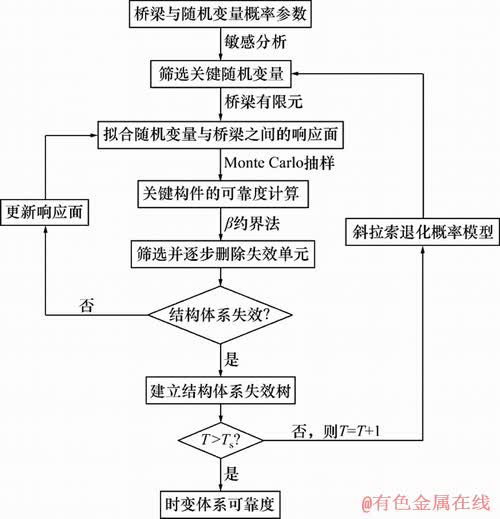
图4　考虑斜拉索损伤的斜拉桥失效路径搜索流程

Fig. 4　Flowchart for searching failure sequences of cable-stayed bridges considering cable damage

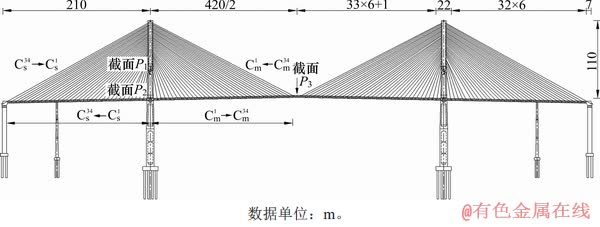
图5　斜拉桥结构尺寸与单元划分图

Fig. 5　Structural dimension and elements division of cable-stayed bridge

图6　斜拉桥有限元模型

Fig. 6　Finite element model of cable-stayed bridge

在ANSYS前处理模块删除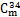拉索，并在34号主梁施加与索力和拉索角度相同的集中力；然后进入瞬态分析模块，在0 s进行当前状态分析，在0.1 s施加与索力数值相同、方向相反的集中力，以模拟断索效应；记录25 s以内的关键构件效应时程曲线，如图7所示。

基于图7所示的动力时程曲线，将静力和动力效应最大值与原始效应值进行对比，得到拉索失效引起的静力与动力增大系数如表1所示。表1中，δ_s与δ_d分别表示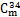拉索断裂后关键构件的静力与动力增大系数。由表1可以看出：斜拉索断裂不仅导致相邻构件的内力增加，而且其动力放大效应不可忽略，如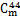拉索断裂导致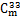拉索索力的静力效应增加0.07，而动力效应最大值达到0.11，为静力效应的84%；离失效拉索较近的构件的放大系数大，而离失效拉索较远的构件的放大系数较小。

3.3　响应面拟合与更新

采用如图4所示的基于响应面方法的失效路径搜索方法拟合斜拉索索力的响应面，其关键步骤为：首先，由均匀设计的1批样本点数据计算结构的非线性效应；由二次序列响应面拟合样本曲面，形成如图8所示的响应面；在有限元模型中删除潜在失效构件，继续进行结构分析与响应面拟合。根据上述步骤即可捕捉到斜拉索逐步失效导致的结构非线性效应。为了分析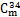拉索断裂前后的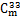拉索索力的响应面，选取拉索截面面积A_s、汽车均布荷载Q为随机变量，采用20个样本的U202均匀设计样本方案，拟合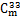拉索索力更新前后的响应面，如图8所示，其中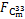，为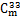索力，U₂₀-2表示均匀设计表中对应的样本数量为20个，参数为2个。

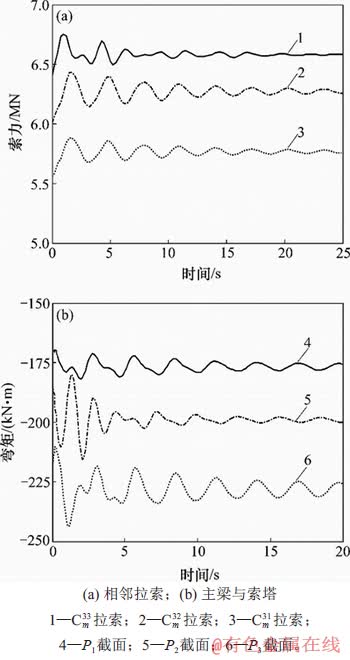
图7　跨中34号单侧斜拉索失效后关键构件响应时程曲线

Fig. 7　Time-history curves of response of the key components considering C_m³⁴ cable failure

表1　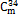拉索断裂后关键构件内力放大系数

Table 1　Amplification factor of inter-force of critical members due to 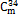cable rupture

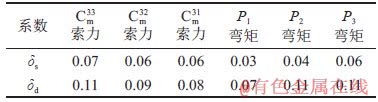
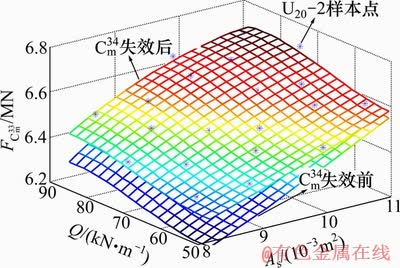
图8　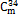拉索失效前后的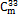拉索索力响应面

Fig. 8　Response surfaces of stay cable force of 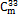cable affected by 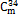cable failure

由图8可知：斜拉索索力响应面边缘呈现非线性特征，仅采用20个样本点即可捕捉到该非线性响应。虽然斜拉桥在正常使用状态下的非线性特征不显著，但在极限状态下的结构行为表现出一定的非线性。此外，采用更新响应面方法可捕捉到拉索断裂引起的内力变化。

基于更新响应面方法，逐步更新结构关键构件的失效构件响应面，直到搜索到斜拉桥结构体系的全部失效路径，并计算相关系数。该斜拉桥在第20年的结构体系失效树如图9所示，图中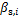表示第i个失效路径的可靠指标。

结合图3所示的斜拉索强度退化概率模型与图9所示失效树，考虑斜拉索的“疲劳”和“腐蚀-疲劳”这2种损伤状态，斜拉桥的结构体系可靠度的时变趋势如图10所示。

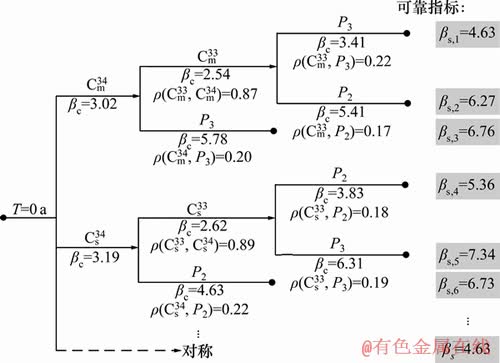
图9　斜拉桥结构体系失效树

Fig. 9　Fault tree of structural system of cable stayed bridge

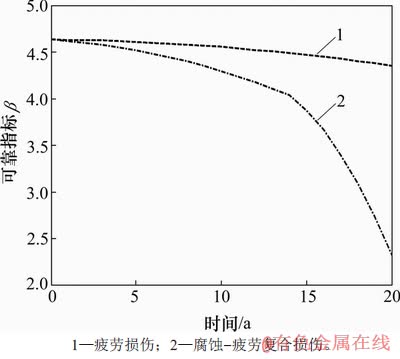
图10　斜拉桥时变体系可靠度

Fig. 10　Time-variant system reliability of cable-stayed bridge

由图10可知：在“疲劳”和“腐蚀-疲劳”这2种损伤作用下，该斜拉桥在第20年的结构体系可靠指标由4.62分别下降至4.42和和2.46，表明腐蚀与疲劳2种损伤的复合作用导致斜拉桥体系可靠度下降趋势较显著。

4 结论

1) 腐蚀和未腐蚀拉索在20 a后的抗拉强度均值分别下降32%和13%，而标准差下降幅度均小于2%，表明基于串-并联模型可捕捉钢丝长度和数量效应对拉索强度概率分布均值和标准差的影响。

2) 单根拉索断裂可导致相邻拉索索力静力效应增加7%，而动力效应达到11%，基于更新响应面方法采用20个均匀设计样本点即可捕捉到该非线性效应。

3) 在“疲劳”和“腐蚀-疲劳”这2种损伤作用下，该斜拉桥在第20年的结构体系可靠指标由4.62分别下降至4.42和和2.46，表明腐蚀效应对斜拉桥运营期体系可靠度影响显著。

参考文献：

[1] 缪长青, 尉廷华, 王义春, 等. 大跨桥梁缆索钢丝腐蚀速率的试验研究[J]. 西南交通大学学报, 2014, 49(3): 513-518.

MIAO Changqing, WEI Tinghua, WANG Yichun, et al. Corrosion rate test of cable wires of large span bridge[J]. Journal of Southeast Jiaotong University, 2014, 49(3): 513-518.

[2] 兰成明, 李惠, 鞠杨. 平行钢丝拉索承载力评定[J]. 土木工程学报, 2013, 46(5): 31-38.

LAN Chengming, LI Hui, JU Yang. Bearing capacity assessment for parallel wire cables[J]. China Civil Engineering Journal, 2013, 46(5): 31-38.

[3] 王立彬, 李爱群, 马小利, 等. 基于寿命函数的斜拉索系统维修更换策略研究[J]. 土木工程学报, 2012, 45(6): 162-170.

WANG Libin, LI Aiqun, MA Xiaoli, et al. Stay-cable maintenance and replacement strategy based on lifetime functions[J]. China Civil Engineering Journal, 2012, 45(6): 162-170.

[4] FABER M H, ENGELUND S, RACKWITZ R. Aspects of parallel wire cable reliability[J]. Structural Safety, 2003, 25(2): 201-225.

[5] LAN Chengming, BAI Nani, YANG Haitao, et al. Weibull modeling of the fatigue life for steel rebar considering corrosion effects[J]. International Journal of Fatigue, 2018, 111: 134-143.

[6] LAN Chengming, XU Yang, LIU Caiping, et al. Fatigue life prediction for parallel-wire stay cables considering corrosion effects[J]. International Journal of Fatigue, 2018, 114: 81-91.

[7] 兰成明, 任登路, 徐阳, 等. 平行钢丝斜拉索疲劳性能评定Ⅱ:斜拉索疲劳寿命模型[J]. 土木工程学报, 2017, 50(7): 69-77.

LAN Chengming, REN Denglu, XU Yang, et al. Fatigue property assessment of parallel wire stay cable Ⅱ: fatigue life model for stay cable[J]. China Civil Engineering Journal, 2017, 50(7): 69-77.

[8] LI Shunlong, XU Yang, ZHU Songye, et al. Probabilistic deterioration model of high-strength steel wires and its application to bridge cables[J]. Structure and Infrastructure Engineering, 2015, 11(9): 1240-1249.

[9] 刘沐宇, 陈齐风, 吴志强. 考虑微动疲劳的斜拉桥钢绞线斜拉索时变可靠性分析[J]. 土木工程学报, 2012, 45(7): 141-147.

LIU Muyu, CHEN Qifeng, WU Zhiqiang. Time-dependent reliability analysis of strand cables of cable-stayed bridges considering fretting-fatigue factor[J]. China Civil Engineering Journal, 2012, 45(7): 141-147.

[10] 鲁乃唯, 刘扬, 肖新辉, 等. 基于联合智能算法的大跨度斜拉桥体系可靠度评估[J]. 应用力学学报, 2015, 32(5): 858-864, 902.

LU Naiwei, LIU Yang, XIAO Xinhui, et al. System reliability assessment of cable-stayed bridges based on a combined intelligent algorithm[J]. Chinese Journal of Applied Mechanics, 2015, 32(5): 858-864, 902.

[11] LU Naiwei, LIU Yang, BEER M. System reliability evaluation of in-service cable-stayed bridges subjected to cable degradation[J]. Structure and Infrastructure Engineering, 2018, 14(11): 1486-1498.

[12] 黄侨, 任远, 许翔, 等. 大跨径缆索承重桥梁状态评估的研究现状与发展[J]. 哈尔滨工业大学学报, 2017, 49(9): 1-9.

HUANG Qiao, REN Yuan, XU Xiang, et al. Research progress of condition evaluation for large span cable supported bridges[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 1-9.

[13] 曹珊珊, 雷俊卿, 黄祖慰. 大跨多线公铁两用斜拉桥索锚结构疲劳荷载效应[J]. 中南大学学报(自然科学版), 2017, 48(12): 3301-3308.

CAO Shanshan, LEI Junqing, HUANG Zuwei. Analysis of fatigue load amplitude of cable-girder anchorage structure in long-span highway-railway cable-stayed bridge[J]. Journal of Central South University(Science and Technology), 2017, 48(12): 3301-3308.

[14] 李延强, 赵世英, 杜彦良. 基于最敏感斜拉索张力指标的斜拉桥主梁损伤识别方法[J]. 中国铁道科学, 2014, 35(2): 20-25.

LI Yanqiang, ZHAO Shiying, DU Yanliang. Damage identification method for the main girder of cable-stayed bridge based on the tension indices of the most sensitive stay cable[J]. China Railway Science, 2014, 35(2): 20-25.

[15] LI Hui, LAN Chengming, JU Yang, et al. Experimental and numerical study of the fatigue properties of corroded parallel wire cables[J]. Journal of Bridge Engineering, 2012, 17(2): 211-220.

[16] BRUNEAU M. Evaluation of system-reliability methods for cable-stayed bridge design[J]. Journal of Structural Engineering, 1992, 118(4): 1106-1120.

[17] LIU Yang, LU Naiwei, YIN Xinfeng, et al. An adaptive support vector regression method for structural system reliability assessment and its application to a cable-stayed bridge[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2016, 230(2): 204-219.

[18] 刘扬, 鲁乃唯, 蒋友宝. 结构体系可靠度分析的改进支持向量回归[J]. 浙江大学学报(工学版), 2015, 49(9): 1692-1699.

LIU Yang, LU Naiwei, JIANG Youbao. Adaptive support vector regression method for structural system reliability analysis[J]. Journal of Zhejiang University(Engineering Science), 2015, 49(9): 1692-1699.

[19] 孙华怀, 陈惟珍, 杨建喜. 锈蚀断丝对拉索力学性能影响的数值研究[J]. 华南理工大学学报(自然科学版), 2018, 46(7): 137-144.

SUN Huahuai, CHEN Weizhen, YANG Jianxi. A numerical study of the effect of corrosion and breakage of wires on mechanical properties of cable[J]. Journal of South China University of Technology(Natural Science Edition), 2018, 46(7): 137-144.

（编辑 陈灿华）

收稿日期： 2019 -03 -05; 修回日期： 2019 -05 -22

基金项目(Foundation item)：国家重点基础研究发展规划(973计划)项目(2015CB057701)；国家自然科学基金资助项目(51678068)(Project(2015CB057701) supported by the National Basic Research Development Program(973 Program) of China; Project(51678068) supported by the National Natural Science Foundation of China)

通信作者：郭鑫，博士研究生，从事桥梁结构可靠度评估与安全控制研究；E-mail:530220383@qq.com