DOI: 10.11817/j.issn.1672-7207.2016.07.029

基于安全系数和可靠度的极破碎矿体进路优化

尚雪义¹，李夕兵¹，彭康²，徐欣¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆，400044)

摘要：基于极破碎矿体开采条件极其复杂、难以确定合理的进路断面参数等问题，建立下向进路薄板力学模型，得到进路承载层抗拉强度破坏判据。在此基础上运用安全系数法和可靠度理论研究进路宽度和高度对承载层拉应力的影响，并对这2种方法所得结果进行比较优化出最佳进路断面，进而开展ABAQUS数值模拟和现场试验验证断面优化的合理性。研究结果表明：进路宽度对承载层拉应力的影响较大，可采用“小宽度、大高度”的思路优化断面；安全系数和可靠度分析结果存在一定差异，且可靠度分析更合理；数值模拟结果与工业试验结果及可靠度分析结果较吻合，表明采用可靠度理论优化极破碎矿体进路断面是可行的，可实现极破碎矿体安全高效经济开采。

关键词：薄板模型；安全系数；可靠度分析；数值模拟；位移监测

中图分类号：TD852          文献标志码：A         文章编号：1672-7207(2016)07-2390-08

Optimization of drift in extremely fractured ore-body based on safety coefficient and reliability analysis

SHANG Xueyi¹, LI Xibing¹, PENG Kang², XU Xin¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China)

Abstract: Considering that in the complicated mining conditions in extremely fractured ore-body, it is difficult to determine a reasonable cross section of drift, a mechanical thin plate model of downward drift and a failure criterion of tensile strength were studied when bearing layer collapsed was obtained. Then effects of drift width and height on tensile strength of bearing layer were studied by means of safety coefficient method and reliability analysis, and the best cross section of drift was gotten sequently by comparing results between these two methods. Moreover, ABAQUS numerical simulation and commercial test were conducted to validate the rationality of the most optimal cross section. The results show that the influence of drift width on tensile strength of bearing layer is more significant than that of drift height, and so an idea of small width and large height should be adopted to optimize cross section. There are some differences between safety coefficient and that of reliability analysis, and the latter is more reasonable. The numerical simulation and industrial test results are in good agreement with those obtained from reliability analysis, which indicates that reliability analysis is feasible in the optimization of drift in extremely fractured ore-body and can achieve safe, efficient and economical mining in extremely fractured ore body.

Key words: thin plate model; safety coefficient; reliability analysis; numerical simulation; displacement monitoring

我国矿产资源丰富，但人均占有量少，随着社会建设和经济的飞速发展，矿产资源需求量急速增长，国内开采条件较好的资源正日益减少^[1]，极破碎等难采矿体的回采亟待解决。对极破碎矿体进行回采可提高矿产资源利用率，延长矿山服务年限，改善矿山企业的管理条件，加速流动资金周转，增大经济效益。然而，极破碎矿体开采条件极为复杂，矿石间黏结力低，回采过程中受自重、打眼、爆破、出矿、渗流等综合因素作用，容易出现冒顶、片帮等问题，作业安全性差。目前，极破碎矿体回采主要采用崩落法和下向充填法^[2]，崩落法贫化损失大，容易造成地表塌陷，而下向进路法回收率高、贫化损失小，使用率迅速上升。随着无轨设备在地下金属矿山的推广应用，下向进路法已进入现代化采矿技术之列^[3]，安全高效经济的进路断面确定就显得尤为重要。从国内外相关文献看，目前针对下向进路优化的研究主要有充填配比优化^[4]、弹性力学分析^[5-7]、相似材料模拟^[8]、现场监测^[9-10]、数值模拟^[11-13]和安全系数法^{[5, 14]}等。充填配比优化运用数学方法得到一定强度下的最优配比，但未对进路断面参数进行优化；运用弹性力学分析得到了下向进路薄“板”和简支“梁”理论模型，但未对下向进路展开定量计算；相似模型试验和现场监测研究承载层位移效果较好，但作为断面优化方法成本高、周期长；采用数值模拟得到了承载层应力、变形及变化规律，但其结果只能作为参考依据，由此开展下向进路理论计算很有必要。安全系数法计算方便，但安全系数的确定方法尚不够完善，往往偏于保守，导致可靠度低。此外，安全系数法将下向进路影响参数视为定值，这与矿山实际开采中各参数受多因素影响为非定值相矛盾，极破碎矿体各参数不确定性更严重。可靠度理论具有明确的可靠度指标，同时能解决各参数存在的不确定性，为此引入可靠度理论对极破碎矿体断面进行优化分析，并将其与常规安全系数法结果比较，以期得到一种安全经济的进路断面优化方法。本文以山东玲珑金矿灵山矿区极破碎矿体进路开采为工程背景，通过现场取样并进行室内试验得到矿岩及充填体物理力学参数，建立下向进路薄板力学模型，将可靠度分析结果与传统安全系数法结果进行比较，并优选出最佳进路断面。

1  工程概况

1.1  工程背景

山东黄金集团有限公司玲珑金矿是我国最大的黄金矿山之一^[15-16]，由位于玲珑金矿的玲珑主矿区和位于焦家断裂带的灵山分矿2 部分组成。灵山分矿主矿体受断裂蚀变带控制，走向NE，倾角为30°~60°，倾向SE，倾角为54°~86°；平均厚度为8.87 m，平均品位为4.96 g/t。矿石类型为碎裂状花岗岩，裂隙发育，稳固性差；矿体上盘断层泥、糜棱岩发育，易脱落，局部掉块现象严重；矿体下盘直接围岩均为钾化花岗岩，间接围岩为黑云母花岗岩，中等稳固。目前，矿山选用机械化盘区C料尾砂下向进路充填采矿法进行回采，采用盘区下向多进路回采方式、下盘脉外斜坡道+分段运输平巷采准系统、无轨设备凿岩出矿及C料尾砂胶结充填技术，采矿工艺水平先进，而与之相适应的进路断面亟待确定。

1.2  力学参数和地应力规律

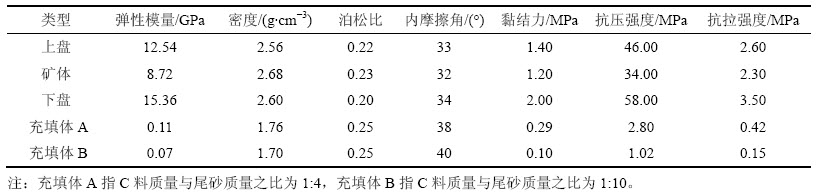
通过对灵山矿区岩体工程地质调查、上下盘岩石取样测试及充填体强度试验，得出灵山矿区矿岩和充填体力学参数如表1所示。

矿区地应力分布规律为^[17]

           (1)

式中：，和分别为最大水平主应力、最小水平主应力和垂直主应力(MPa)；H为测点埋深(m)。

表1  矿岩和充填体力学参数

Table 1  Mechanical parameters of ore rock and backfill

2  进路开采稳定性分析及优化

2.1  进路回采薄板模型

根据下向进路开采中承载层受力特征，对灵山矿区进路开采进行如下假设：1) 进路承载层为连续、均匀、各向同性介质，符合弹性板的假设条件；2) 矿岩和承载层在屈服破坏之前为线弹性体；3) 承载层受载为均布荷载；4) 开采中进路长度远大于进路宽度，满足平面应变假设。由此可将进路侧帮视为弹性基础，将承载层视为弹性基础之上由弹性介质组成的薄板进行研究(图1)，并得到如下计算式^[18]。

图1  下向进路薄板力学模型及受力分析

Fig. 1  Mechanical model of thin plate and stress analysis of downward drift

1) 当时，处弯矩有极值(不考虑弯矩作用方向)：

，

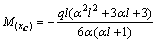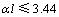
式中：。

2) 当x＞l时(x＜ -l与其对称)， 处弯矩有极大值：

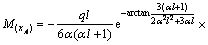
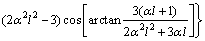, al＞3.44

式中：M₀为阻滞载层所受弯矩；x_C和x_A分别为C点和A点与坐标原点的距离；为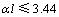时最大弯矩；为al＞3.44时最大弯矩；E_j为进路侧帮基础弹性模量；E_L为顶板的弹性模量；为充填体的泊松比；h为顶板厚度，一般h≤1.5 m；l为进路宽度之一半，一般l≥1.25 m；M为进路高度。由此得到下向进路最大拉应力计算式为

      (2)

以此作为确定充填体稳定性的判据。若承载层下表面拉应力超过其抗拉强度，则认为充填体发生失稳破坏。式(2)中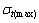，为承载层计算最大拉应力。

对灵山矿区现场进行观察，发现承载层的稳定性较好，补口层和接顶层稳定性较差，故每个分层所受荷载可视为只受承载层和普通充填体的自重，即

              (3)

式中：q为承载层所受荷载，kPa；为承载层容重，kN/m³；为补口层和接顶层容重，kN/m³。

2.2  安全系数法分析

灵山分矿原高水固结全尾砂下向进路充填采矿法进路宽度L=3.0 m，高度M=3.0 m，承载层厚度h=1.0 m。进路沿矿体走向时由上盘向下盘连续回采，垂直矿体走向时隔一采一，因此，矿体回采中“硬支薄板”、“软硬支混合”、“软支薄板”结构均有，由文献[18]知“软支薄板”结构最易破坏，故可只对“软支薄板”结构进行分析。

下向进路承载层的稳定性是进路回采的关键，因此，承载层所受拉应力需留有一定的安全储备，为此引入下向进路稳定性的安全系数判别式(4)。地下矿山安全开采经验表明安全系数应为1.6~1.8^[19]，鉴于灵山矿区矿岩极破碎，本文取＞1.8作为下向进路稳定条件的评价标准。

               (4)

式中：为安全系数；为承载层所能承受的最大拉应力。为研究下向进路稳定性受进路宽度和高度的影响，采用控制变量法对不同进路半宽和高度下安全系数随承载层厚度的变化进行研究，得到M=3.0 m时不同进路半宽l下承载层厚度与安全系数关系曲线(图2)和l=1.5 m时不同进路高度M下承载层厚度与安全系数关系曲线(图3)。

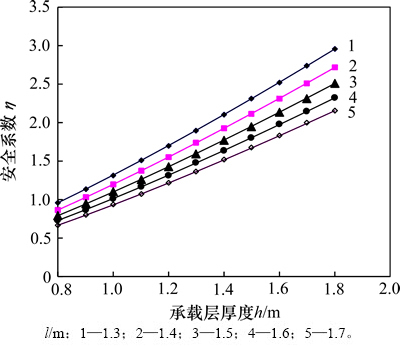
图2  不同进路半宽l下承载层厚度与安全系数的关系

Fig. 2  Relationship between loading layer thickness and safety coefficient with different half drift widths

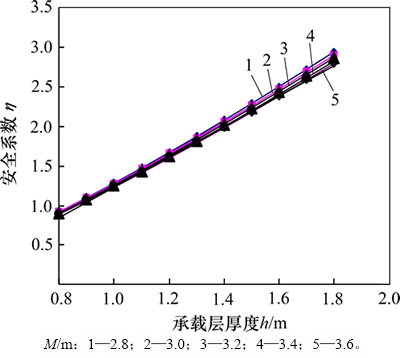
图3  不同进路高度M下承载层厚度与安全系数的关系

Fig. 3  Relationship between loading layer thickness and safety coefficient with different drift heights

由图3可知：1) 灵山矿区现有进路l=1.5 m， M=3.0 m，h=1.0 m，安全系数仅为1.27，远低于要求值1.80，承载层厚度应提高到大于1.27 m(=1.8)才可保证矿山安全开采；2) 下向进路安全系数随进路宽度和高度增大而减小，且进路宽度对安全系数的影响较大，而进路高度对安全系数的影响较小，因此，可考虑采用小宽度、大高度进路断面以达到既满足假顶稳定性，又能扩大生产的目的，建议保持进路宽度3.00 m不变，而将进路高度调整为3.60 m，此时对应的承载层厚度为1.50 m(=1.82)。

2.3  可靠度分析

考虑到安全系数法将承载层厚度、承载层抗拉强度、承载层弹性模量、进路两侧帮弹性模量、进路宽度和高度等因素视为定值，未考虑各因素的随机性，且安全系数标准采用经验值，所得出的计算结果与实际结果可能会有较大差距。本文采用蒙特卡罗法对下向进路可靠性进行分析。

2.3.1  蒙特卡罗法分析原理

设功能函数为 (式中，X_i(i=1, 2, …, n)为具有任意分布的随机变量)。对X_i(i=1, 2, …, n)进行N次抽样，得N组(j=1, 2, …, N)，将第j组(j=1, 2, …, N)的(i=1, 2, …, n)代入功能函数，得N个Z_j(j=1, 2, …, N)。令

      (5)

则当N足够大时，结构的可靠度概率P_r近似等于可靠性频率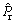，即

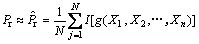        (6)

2.3.2  随机变量特征值及极限状态方程的确定

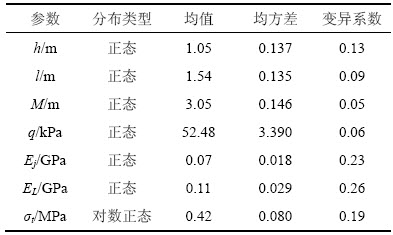
通过现场调查及室内充填实验，得到进路稳定性随机变量概率特征值，见表2。

表2  随机变量概率特征值

Table 2  Statistical characteristic value of primary random variables

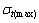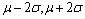可由式(2)确定极限状态方程。对应方程与相关，而中各参数呈现一定分布，不可直接求得，为此只计算其极值。又正态分布在()的概率为0.954 4，完全满足工程设计要求，故的极大值可按下式计算得到：

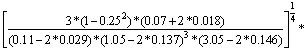
            (7)

故

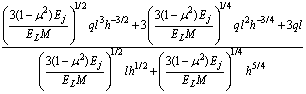(8)

由式(8)可建立下向进路稳定性关于承载层抗拉强度的极限状态方程：

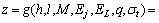
(9)

2.3.3  随机变量均值对可靠度概率影响

对于下向进路胶结充填采矿法而言，承载层稳定性可靠概率达到90%即可满足井下生产的要求^[20]，因此，确定承载层稳定性可靠度概率为90%。根据蒙特卡罗分析原理运用mathematica对式(9)编程，结合表2中各参数分布，采用控制变量法得到不同进路宽度和高度下可靠度概率关系如图4和图5所示。

由图4可知：1) 当只改变1个变量时，l≤1.3 m (P≥0.92)或M≤2.8 m(P≥0.91)可满足可靠度概率，此时开采断面偏小；2) 可靠度概率随进路宽度和高度增加而减小，且进路宽度对可靠度概率的影响较大，与安全系数对可靠度概率的影响规律一致，因此，考虑选择“小宽度、大高度”进路断面。建议保持进路宽度3.00 m不变，而将进路高度调整为3.60 m，此时对应的承载层厚度为1.25 m(P=0.91)。

图4  进路半宽与可靠度概率的关系

Fig. 4  Relationship between a half wide of drift and probability calculation for reliability

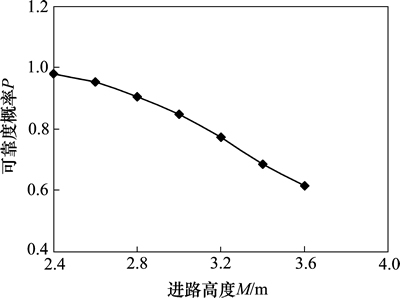
图5  进路高度与可靠度概率的关系

Fig. 5  Relation between drift width and probability calculation for reliability

2.4  安全系数法与可靠度分析比较

由上述分析易得下向进路稳定性安全系数法与可靠度分析关系如图6所示。当进路半宽l=1.3 m时，对应的可靠度概率P=0.93，安全系数；当进路高度M=2.8 m时，对应的可靠度概率P=0.91，安全系数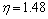，得到可靠度优化不同变量时对应的安全系数不为定值，且安全系数取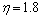偏于保守，故将可靠度优化结果l=1.50 m，M=3.60 m，h=1.25 m (P=0.91)作为设计断面较经济、合理。

图6  安全系数法与可靠度分析比较

Fig. 6  Comparison between safety coefficient method and reliability method

3  进路断面数值模拟

为验证可靠度分析结果的合理性，采用数值模拟对原方案、安全系数方案及可靠度分析方案应力进行分析，同时得到假顶最大位移，可为现场位移监测提供参考。

3.1  数值模型及模拟方案

采用有限元数值分析软件ABAQUS建立下向进路平面应变模型如图7所示。所选矿岩和充填体力学参数见表1。选用摩尔-库仑本构模型，并假设材料为理想弹塑性体。有限元模型两侧面固定水平位移，下表面固定竖直位移，采用3步进行：第1步，施加地应力(取埋深600 m)，形成开挖前的初始应力状态；第2步，间隔开挖进路；第3步，充填开挖进路，开挖矿柱。

图7  进路断面有限元计算模型

Fig. 7  Finite element calculation model of drift cross section

3.2  模型结果分析

沿进路假顶宽度方向布置观察测线，测线长度等于进路宽度，依次记录观察测线处的最大拉应力和位移，绘制不同方案沿测线的最大拉应力和位移如图8所示，并计算其可靠度概率如表3所示。

由图8和表3可知：1) 假顶最大拉应力和位移均出现在假顶中心位置，其值随承载层厚度的增加而减小，且最大拉应力近似抛物线分布，而最大位移在假顶距左端点0~1 m和2~3 m间变化明显，而在1~2 m间变化平缓；2) 原方案假顶可靠度概率仅为0.76，极有可能发生假顶冒落现象；安全系数方案可靠度概率达到0.99，即安全系数方案偏于保守；可靠度方案可靠度概率为0.91，为最佳方案。

图8  假顶最大拉应力和位移

Fig. 8  Maximum tensile stress and displacement of artificial roof

表3  各方案假顶最大拉应力及位移比较

Table 3  Comparison of the maximum tensile stress and displacement among different schemes

4  工业性试验

选取灵山矿区-590-1号盘区作为工业试验场地，矿体上下盘矿岩极破碎，存在隐性三角节理。下向进路回采宽度为3.00 m、高度为3.60 m，采用C料尾砂质量比为1:4、质量分数为70%的料浆进行打底充填1.30 m，剩余高度采用灰砂比1:10、质量分数为70%的料浆进行普通充填和接顶充填。

在1线和2线间选取A，B，C，D和E 5个断面(图9)，采用SWJ-IV隧道收敛计测得假顶中点累积位移随时间变化曲线(图10)。由图10知：假顶位移随时间而增大，且5个监测点位移均有收敛的趋势，假顶中点60 d的累积最大位移为51.50 mm，每天最大位移为3.41 mm，平均位移为1.38 mm。变形量小且未出现突变值，由此得到工业试验是安全的，同时表明可靠度理论优化极破碎矿体进路断面是可行的。

图9  收敛计测量断面位置平面图

Fig. 9  Plan of measuring cross sections of convergence meter

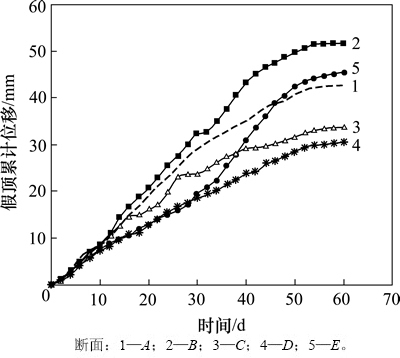
图10  假顶中点累积位移沉降曲线

Fig. 10  Cumulative displacement curves of midpoint of artificial roof

5  结论

1) 针对传统安全系数法将下向进路各影响因素视为定值，而极破碎矿体各参数为非定值且呈现一定分布的特点，引入了可靠度理论展开分析。

2) 建立了下向进路薄板力学模型，得到充填体失稳破坏抗拉强度判据，并运用安全系数法和可靠度分析得到进路宽度对承载层拉应力的影响较大，提出了“小宽度、大高度”的进路断面优化思路。

3) 安全系数法和可靠度分析结果存在一定差异，且安全系数法结果偏于保守，可靠度分析可在保证安全的前提下，更经济地实现极破碎矿体开采。

4) ABAQUS数值模拟结果和现场工业试验结果均与可靠度分析结果吻合良好，表明可靠度理论优化极破碎矿体进路断面是可行的，可实现极破碎矿体安全高效、经济开采。

参考文献：

[1] 古徳生, 李夕兵. 现代金属矿床开采科学技术[M]. 北京: 冶金工业出版社, 2006: 1-2.

GU Desheng, LI Xibing. Modern mining science and technology for metal mineral resources[M]. Beijing: China Metallurgical Industry Press, 2006: 1-2.

[2] 李夕兵, 范文录, 胡国宏. 急倾斜破碎矿体采矿方法改进与顶板再造设计[J]. 科技导报, 2012, 30(13): 44-48.

LI Xibing, FAN Wenlu, HU Guohong. Improvement of steep and fractured ore-body mining method and design of re-construction of sub-top[J]. Science & Technology Review, 2012, 30(13): 44-48.

[3] DE SOUZA E, DEGAGNE D, ARCHIBALD J F. Minefill applications, practices and trends in Canadian mines[C]// Minefill 2001: 7th International Symposium on Mining with Backfill. Seattle, America, 2001: 311-319.

[4] 韩斌, 吴爱祥, 王贻明, 等. 低强度粗骨料超细全尾砂自流胶结充填配合比优化及应用[J]. 中南大学学报(自然科学版), 2012, 43(6): 2357-2362.

HAN Bin, WU Aixiang, WANG Yiming, et al. Optimization and application of cemented hydraulic fill (CHF) with low strength aggregate and extra fine grain full tailings[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2357-2362.

[5] 赵彬. 焦家金矿尾砂固结材料配比试验及工艺改造方案研究[D]. 长沙: 中南大学资源与安全工程学院, 2009: 1-30.

ZHAO Bin. Study of tailing-cemented materials proportion and backfilling technology transformation[D]. Changsha: Central South University. School of Resources and Civil Engineering, 2009: 1-30.

[6] O'HEARN B, SWAN G. The use of models in sill mat design at Falconbridge[C]// Innovations in Mining Backfill Technology: Proceedings of the 4th International Symposium on Mining with Backfill. Brookfield, America, 1989: 139-146.

[7] 顾伟, 张立亚, 谭志祥, 等. 基于弹性薄板模型的开放式充填顶板稳定性研究[J]. 采矿与安全工程学报, 2013, 30(6): 886-891.

GU Wei, ZHANG Liya, TAN Zhixiang, et al. Study on roof stability of open backfilling based on elastic plate model[J]. Journal of Mining & Safety Engineering, 2013, 30(6): 886-891.

[8] 周科平, 朱和玲, 高峰. 采矿环境再造地下人工结构稳定性综合方法研究与应用[J]. 岩石力学与工程学报, 2012, 31(7): 1429-1436.

ZHOU Keping, ZHU Heling, GAO Feng. Research on stability of reconstructed underground artificial structure in mining environment by comprehensive method and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1429-1436.

[9] 冯仲仁, 张兴才, 张世雄, 等. 大冶铁矿巷道变形监测研究[J]. 岩石力学与工程学报, 2004, 23(3): 483-487.

FENG Zhongren, ZHANG Xingcai, ZHANG Shixiong, et al. Monitoring study on drift deformation of Daye iron mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(3): 483-487.

[10] TESARIK D R, SEYMOUR J B, YANSKE T R. Long-term stability of a backfilled room-and-pillar test section at the Buick Mine, Missouri, USA[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(7): 1182-1196.

[11] 董金奎, 冯夏庭, 张希巍, 等. 地下采场破碎岩体稳定性评价与参数优化[J].东北大学学报(自然科学版), 2013, 34(9): 1322-1326.

DONG Jinkui, FENG Xiating, ZHANG Xiwei, et al. Stability evaluation and parameter optimization on the fractured rock mass around underground stope[J]. Journal of Northeastern University (Science and Technology), 2013, 34(9): 1322-1326.

[12] 付玉凯, 鞠文君. 影响软岩巷道变形因素的正交数值模拟试验研究[J]. 采矿与安全工程学报, 2013, 30(6): 812-816.

FU Yukai, JU Wenjun. Study on affecting factors of soft rock deformation with orthogonal numerical simulation test[J]. Journal of Mining & Safety Engineering, 2013, 30(6): 812-816.

[13] HUGHESA P, PAKALNISA R, CACERESA C, et al. Numerical modeling of paste sills in underhand cut & fill stopes[C]// Third International Seminar on Deep and High Stress Mining. Quebec City, Canada, 2006: 1-10.

[14] 彭康, 李夕兵, 彭述权, 等. 海底下框架式分层充填法开采中矿岩稳定性分析[J]. 中南大学学报(自然科学版), 2011, 42(11): 3452-3458.

PENG Kang, LI Xibing, PENG Shuquan, et al. Ore-rock stability of frame stope hierarchical level filling mining method in seabed mining[J]. Journal of Central South University (Science and Technology), 2011, 42(11): 3452-3458.

[15] 王玉白, 张宪堂, 李树忱. 玲珑金矿深部应力分析及岩爆防治措施研究[J]. 岩土力学, 2006, 27(增刊): 1401-1404.

WANG Yubai, ZHANG Xiantang, LI Shuzhen. Analysis of deep rock stress and prevention methods of rock burst in Linglong gold mine[J]. Rock and Soil Mechanics, 2006, 27(Suppl): 1401-1404.

[16] 蔡美峰, 孔留安, 李长洪, 等. 玲珑金矿主运巷塌陷治理区稳定性动态综合监测与评价[J]. 岩石力学与工程学报, 2007, 26(5): 886-894.

CAI Meifeng, KONG Liuan, LI Changhong, et al. Dynamic comprehensive monitoring and assessment of stability of collapsed area after supporting in main transport roadway in Linglong gold mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 886-894.

[17] 蔡美峰, 刘卫东, 李远. 玲珑金矿深部地应力测量及矿区地应力场分布规律[J]. 岩石力学与工程学报, 2010, 29(2): 227-233.

CAI Meifeng, LIU Weidong, LI Yuan. In-situ stress measurement at deep position of Linglong gold mine and distribution law of in-situ stress field in mine area[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 227-233.

[18] 孙恒虎, 刘文永, 黄玉诚, 等. 高水固结充填采矿[M]. 北京: 机械工业出版社, 1998: 313-317.

SUN Henghu, LIU Wenyong, HUANG Yucheng, et al. Mining technology backfilled by high-water solidified material[M]. Beijing: China Machine Press, 1998: 313-317.

[19] 陈玉民, 李夕兵. 海底大型金属矿床安全高效开采技术[M]. 北京: 冶金工业出版社, 2013: 196-196.

CHEN Yumin, LI Xibing. Research on technology of efficient and safe mining in large-undersea metal deposit[M]. Beijing: Metallurgical Industry Press, 2013: 196-196.

[20] 范文录, 李夕兵, 周子龙. 基于可靠度理论的钢筋混凝土假顶强度确定与配筋设计研究[J]. 矿冶工程, 2013, 33(4): 30-35.

FAN Wenlu, LI Xibing, ZHOU Zilong. Strength determination for reinforced concrete false roof and reinforcement design based on reliability theory[J]. Mining and Metallurgical Engineering, 2013, 33(4): 30-35.

(编辑  陈灿华)

收稿日期：2015-07-12；修回日期：2015-09-22

基金项目(Foundation item)：国家自然科学基金资助项目(41272304)；中南大学博士研究生自主探索创新项目(2015zzts075) (Project (41272304) supported by the National Natural Science Foundation of China; Project(2015zzts075) supported by Cultivating Excellent PhDs of Central South University)

通信作者：李夕兵，教授，博士生导师，从事采矿与岩土工程研究；E-mail: xbli@mail.csu.edu.cn