文章编号：1004-0609(2015)-03-0799-07

500 kA级铝电槽内氧化铝浓度场的数值模拟

江  南¹，邱泽晶²，张翮辉¹，张红亮¹，杨  帅¹，李  劼¹，刘庆生³

(1. 中南大学 冶金与环境学院，长沙 410083；

2. 南瑞(武汉)电气设备与工程能效测评中心，武汉 430074；

3. 江西理工大学 冶金与化学工程学院，赣州 341000)

摘  要：在深入分析铝电解槽流体体系及氧化铝消耗机理的基础上，建立某500 kA特大型铝电解槽内氧化铝输运过程的多组分多相瞬态模型，并在CFX12.0平台上实现全槽氧化铝浓度分布情况的瞬态解析。结果表明：研究的500kA级铝电槽内氧化铝浓度场受熔体流动影响而具有显著的时间性和槽内空间性差异。下料后很短的时间内，在下料点正下方区域的氧化铝浓度急剧增加，达到最大值3.9%(质量分数)；之后，随着电解质的流动，不断分散回落到2.8%左右。在推动氧化铝的输运上，阳极气泡对氧化铝传质的驱动作用比电磁力大，但范围没有电磁力广。

关键词：铝电解；氧化铝浓度；数值仿真；浓度场

中图分类号：TF821　　     文献标志码：A

Numerical simulation of alumina concentration field in 500 kA aluminum reduction cell

JIANG Nan¹, QIU Ze-jing², ZHANG He-hui¹, ZHANG Hong-liang¹, YANG Shuai¹, LI Jie¹, LIU Qin-sheng³

(1. School of Metallurgy and Environment, Central South University, Changsha 410083, China;

2. NANRI (Wuhan) Electrical Equipment and Engineering Efficiency Evaluation Center, Wuhan 430074, China;

3. School of Metallurgical and Chemical Engineering,

Jiangxi University of Science and Technology, Ganzhou 341000, China)

Abstract: Based on the in-depth analysis of aluminium reduction cell fluid system and the mechanism of alumina consumption characteristics, the transient multicomponent and multiphase model for simulating the transport process of alumina in 500 kA aluminum reduction cells was developed in CFX12.0, which realized the accurate transient analysis of the alumina concentration distribution within the whole cell. The results show that the alumina concentration field which is affected by the melt flow has significant difference of timeliness and spatiality of cell. In a short period after feeding, alumina concentration below discharging points increases to maximum of 3.9% (mass fraction) sharply, and then decreases to around 2.8% as the electrolyte flows continuously. In promoting the alumina transport, the effect of anode bubble on the alumina mass transfer is greater than the electromagnetic force, but the affected range of anode bubble is smaller than that of electromagnetic force.

Key words: aluminium electrolysis; alumina concentration; numerical simulation; concentration field

在预焙铝电解槽内，氧化铝按照一定的时间间隔，以点式下料方式加入熔体，在其输运过程中完成溶解、扩散及对流的传质过程，为电解反应提供原料。氧化铝的输运过程与槽内电解状况密切相关，良好的氧化铝输运是电解过程稳定进行和高电流效率的前提条件，若氧化铝输运过程受阻，可能会产生该部分电解质温度过低、产生槽底沉淀等问题，进而造成电压波动和阳极效应，导致电解能耗升高。MOXNES等^[1]通过对工业电解实验研究证实上述观点。因此，对电解质内氧化铝的溶解与输运过程进行研究，对于槽型的设计与工艺优化具有重要意义。

氧化铝在电解质中的溶解行为是一个涉及传热、传质和化学反应的复杂过程。为了获得较为均匀的氧化铝浓度分布和较高的输运效率^[2]，必须对铝电解槽内氧化铝的输运过程进行深入研究，鉴于电解质的高温和强腐蚀性的制约，相关工业试验的难度和成本很高，而CFD的手段则提供了一条很好的研究途径^[3-4]。FENG等^[5-6]对铝电解槽内氧化铝输运过程进行了数值模拟，研究下料点位置、下料策略和相关铝电解槽结构参数对氧化铝浓度分布的影响，但忽略电磁力对电解质流场的影响。夏小霞等^[7]以某156kA铝电解槽为研究对象，在CFX 4.3平台上分别研究了仅电磁力作用时、仅阳极气泡作用时以及二者同时作用时，电解质主要沿阳极进行区域循环运动，但是建立的是三维半槽模型，而实际上槽内电磁力的分布往往并非对称，且流场计算网格的单元数目不足50000，故其可靠性和计算精度尚有待提高。

学术界关于氧化铝在电解质中的行为的基础研究，包括溶解度和近似溶解速度等指标^[8]，在溶解过程的反应机理和形态变化方面，建立了诸多数学模型来加以描述。ROLSETH等^[9]基于氧化铝溶解的实验数据归纳得到半经验模型，HAVERKAMP等^[10]提出了化学反应控制模型，此外，LILLEBUEN等^[11]结合POI等^[12]的研究建立传质控制模型，BEREZIN等^[13]和BLATCH等^[14]分别提出传热控制模型和传热传质耦合模型，KAENEL等^[15]对氧化铝的扩散和输运过程进行了数值模拟研究。在国内，徐宁等^[16]通过对氧化铝晶体在冰晶石中溶解产物结构的分析，建立了氧化铝在冰晶石中的中间态活化络离子动力学模型过程的动力学模型。张家齐^[17]提出氧化铝溶解的通用模型，考虑了氧化铝和电解质的质对氧化铝溶解造成的影响，但是该模型十分复杂，并引入了大量的假设参数和准数，且准数的适用性尚值得推敲。

总的说来，诸多理论模型都是在较为严格的假设和特定的实验槽情况下建立的，但只侧重于某一个方面，其应用受到假设条件、参数获取、准数适用性和工艺条件波动等诸多限制。对现代大型铝电解槽而言，随着电流强度的提高，单位时间内氧化铝下料量明显增大，槽型尺寸的增加，这迫切需要运用新的数学模型来准确模拟氧化铝的输运过程。因此，本文作者紧密结合电磁场的分布特点，建立氧化铝输运过程的多组分多相流数学模型并通过解法分析和计算实验提高计算的稳定性和收敛性，阐明氧化铝输运过程的动力学行为和内在特征。

1  氧化铝输运过程的多组分多相流模型

1.1  电解质的拟均相假设与简化

从氧化铝全槽输运的整体性出发，提出电解质的拟均相流假设，将电解质视为由冰晶石和氧化铝两种组分组成的均相流体，这两种组分不发生宏观上的掺混，氧化铝伴随电解质的流动而在全槽输运，采用欧拉法给予描述。在此基础上，建立氧化铝输运过程的多组分多相流瞬态模型，并提出如下模型假设与简化：1) 电解质视为恒温的不可压缩流动，且槽帮形状保持恒定；2) 阳极底掌平整，极距保持恒定；3) 忽略铝液层的存在，将电解质的底面视为电解质-铝液界面(阴极)；4) 阳极气体为具有相等直径的气体颗粒，故可处理为离散相。

因此，本模型中包含电解质(连续相)和阳极气泡(离散相)两相，而电解质相则包含了冰晶石和氧化铝两种组分，建立模型的主要目的是为了模拟氧化铝组分的瞬态输运过程。

1.2  流体控制方程

基于欧拉/欧拉的方法通过求解简化的时均Navier-Stokes方程来模拟三维的电解质-阳极气泡两相流，控制流体运动的质量守恒方程和动量守恒方程分别如下所示：

                   (1)

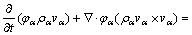
(2)

式中：φ_a、r_a、v_a、p_a和m_aeff分别为α相的体积分数、密度、速度、压强和有效黏度，其中有效黏度为分子粘度和涡流黏度之和，而各相的体积分数之和必须为1，以满足体积守恒条件；M_a为相间的动量传递，包括电解质和铝液两相间的曳力以及电解质和阳极气泡颗粒之间的曳力作用；为外部作用力。

在模型中电解质相为第一相，而氧化铝和冰晶石分别为电解质相中的A组分和B组分，则对电解质相还需要增加组分守恒方程，亦即氧化铝的质量输运方程如下所示：

  (3)

式中：从左至右分别为i组分的质量变化项、对流项、扩散项和源项；r₁、r₁和U₁分别为电解质相的体积分数、密度和速度；Y_i1、D_i1和S_i1则分别为电解质相中i组分的质量分数、扩散系数和质量源项。

同时，同一相中各组分的质量分数之和恒为1：

                                (4)

对于多组分流的数值求解，一般的处理方法是将各种组分所处的流体相作为一个整体，求解主体流动过程的速度、压力、温度和湍动强度等参数；多组分对流场的影响主要通过所处流动相属性的变化来体现。

1.3  氧化铝消耗与下料过程的质量源项

对于氧化铝的电解消耗过程，近似认为氧化铝全部在电解质-铝液界面(阴极表面)发生还原，故其消耗为界面上的分布函数；对于氧化铝的下料过程，则是一个与下料时间间隔相关的瞬态周期性函数。对这一过程，可以应用质量源项函数对其进行描述。

1.3.1  氧化铝电解消耗过程

根据法拉第定律，铝电解槽内的产铝量可以表示为

                              (5)

式中：P为产铝量(kg)；C为铝的电化学当量(0.3356 g·A^-1·h^-1)；τ为电解时间(h)；η为电流效率。

可推出氧化铝的质量消耗速率公式如下所示：

                          (6)

式中：m_loc为氧化铝的局部消耗速率(kg·s^-1·m^-2)；J_b为电解质底面的电流密度分布(A/m²)。

1.3.2  氧化铝下料过程

氧化铝并非在下料的瞬间就进入电解质主体，而是一定的时间滞后性，且其逐渐溶解进入电解质相的过程亦需要一定的时间，故提出氧化铝下料过程的质量源项时变函数为

       (7)

式中：T₀为铝电解槽的基准下料周期，为理论计算得到的固定值；m₀为全槽氧化铝的消耗速率(kg/s)；n为下料点的数目；τ′为从下料时刻到氧化铝开始进入电解质主体时刻的时间滞后量；δ为氧化铝溶解进入氧化铝相所需的时间；ω和q分别为与单个下料间隔T有关的频率与函数左移量，方程式如下所示：

                                    (8)

                                  (9)

式(8)和(9)中的下料间隔周期T不同于式(7)中固定不变的基准下料周期T₀，而是由铝电解槽控制系统决定，可根据需要而调整：对正常的基准下料，T=T₀；对过料下料，则间隔缩短，T＜T₀；对欠料下料，则周期延长，T＞T₀。针对不同的槽型,相关参数是根据特定槽型计算而得。

2  模型的瞬态计算及其实现

针对某超大型500 kA铝电解槽，进行槽内氧化铝输运过程的数值仿真研究。该电解槽设计有6个下料点，各下料点的位置如图1所示。该工艺下电解质中氧化铝的扩散系数为1.5×10^{-9 m2}/s^[18]。

在获得全槽电磁场分布的基础上，引入氧化铝组分的质量源项函数以建立电解质中氧化铝输运过程的多组分多相流模型，并在CFX12.0平台上实现其瞬态计算，解决数值计算的收敛性和稳定性等问题。

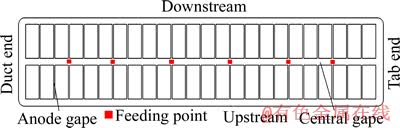
图1  某500 kA铝电解槽的下料点位置示意图

Fig. 1  Schematic diagram of feeding positions in 500 kA aluminum reduction cell

通过查阅文献以及对当前先进铝电解槽工艺参数的调查可知，大型预焙铝电解槽氧化铝浓度一般控制在2.5%(质量分数)左右为宜，因此，假设初始时刻槽内各处氧化铝浓度均为2.5%，并计算得到稳态流场作为后续瞬态求解的初始条件。铝电解槽内氧化铝输运过程的数值求解过程包含如下关键步骤：

1) 电磁力和电流密度分布的计算：在ANSYS平台上进行电磁场计算，获得电解质区域的电磁力分布和电解质底部的电流密度分布，并将电解质底部的电流密度分布整理成(x，y，J_b)的形式；

2) 多组分多相流模型初始条件的计算：将第1)步中得到的电磁力分布导入CFX平台，进行包含电磁力作用的电解质-阳极气泡两相流稳态计算，并得到结果文件；

3) 质量源项的计算：将第1)步中得到的电流密度分布按照式(6)计算得到氧化铝消耗的质量源项函数，并整理成(x，y，m_loc)的形式；同时按照式(7)计算得到氧化铝下料过程的质量源项时变函数的表达式；

4) 多组分多相流模型瞬态模型的建立：在CFX平台上将第2)步设置的电解质-阳极气泡两相流模型由稳态计算变更为瞬态计算，并在模型中添加由第3)步得到的质量源项函数。其中下料过程所加入的氧化铝组分的质量源项作用在各个下料点正下方且靠近电解质表面的对应的小立方体内，而消耗的质量源项则作用在电解质底部平面上；

5) 多组分多相流模型瞬态模型的数值求解：将第2)步得到的结果文件作为初始条件，对第4)步设置好的瞬态模型进行数值计算。为了计算的收敛性和效率，计算初期采用较小的时间步长，等计算若干时间步后可将时间步长增加至0.05s左右。由于第2)步稳态模型中的电解质流速和压强项已经收敛并趋于稳定，瞬态迭代过程的主要目的是求解氧化铝组分的浓度分布变化。

考虑周期为60 s的正常下料情况，并结合文献[19]设置式(7)中时间滞后量τ′和氧化铝溶解耗时τ的取值分别为5 s和10 s，则以3个下料周期的时长为例，得到氧化铝下料过程所加入的质量源项f(b)如图2所示。

氧化铝消耗的质量源项和电解质的水平流速分布分别如图3和4所示。

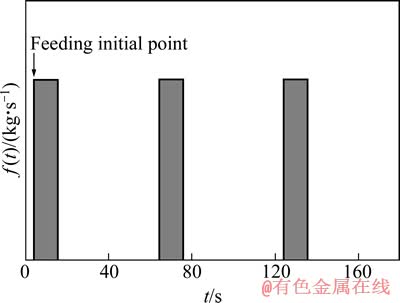
图2  氧化铝下料过程的质量源项时变图

Fig. 2  Time-varying graph of alumina quality source during feeding

可以明显发现，电解质底部各处氧化铝的消耗速率存在着显著的差异，主要体现为如下3个特点：1) 氧化铝的消耗主要集中在广大阳极投影区域，最大消耗速率为1.190×10^{-3 kg}·s^-1·m^-2，而平均值为8.90×10^{-4 kg}·s^-1·m^-2，最大值稍高于平均值高，表明不存在消耗速率明显特别大的区域；2) 阳极中缝和边缝区域的氧化铝消耗较慢，最小消耗速率为3.39×10^{-4 kg}·s^-1·m^-2，远小于平均值，表明直流电从阳极底掌流向阴极的路径基本垂直，水平电流较小，这有利于维持较高的电流效率^[20]；3) 进电侧和出电侧区域的消耗速率对称。

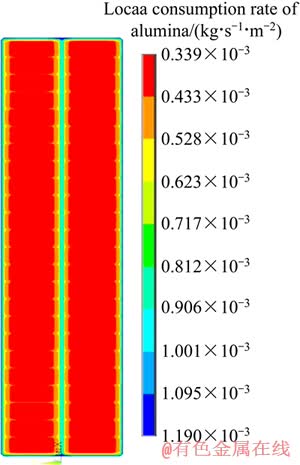
图3  氧化铝的局部消耗速率

Fig. 3  Vector distribution of electrolyte horizontal velocity

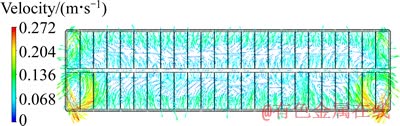
图4  电解质的水平流速矢量分布图

Fig. 4  Vector of bath velocity

如图4所示，电解质区域的水平流速分布存在较大的差异，流速较大的区域主要集中在阳极投影四周和槽子角部区域，进电侧区域的电解质流速与涡运动略大于出电侧的。

由于电解过程中氧化铝下料和消耗的不均匀性，以及电解质区域各处流速的不一致性，造成了氧化铝浓度分布在时间和空间上的差异。取电解质极间区域的水平截面，以10s为时间间隔，得到一个周期内全槽氧化铝浓度分布的时变情况分别如图5(a)~(f)所示，各云图中左侧标尺代表氧化铝浓度的质量分数。

从图5(a)中可以看出，氧化铝下料后起初集中在下料点正下方阳极中缝区域面积很小的范围内，其他区域保持初始浓度不变；随后，在电解质受流体的作用下氧化铝开始分为4小股沿四周逐渐输运，浓度最大值所处的位置由阳极中缝区域向下料点周围的阳极底掌投影区不断移动，且其分布形状体现出一定的漩涡特点(见图5(b)~(d))；最后，氧化铝组分实现了全槽的输运，最大浓度由最初的中缝区域下料点正下方移动至阳极底掌中间位置^[19]，在槽内的广大区域内形成了较为均匀的浓度分布(见图5(e)~(f))。

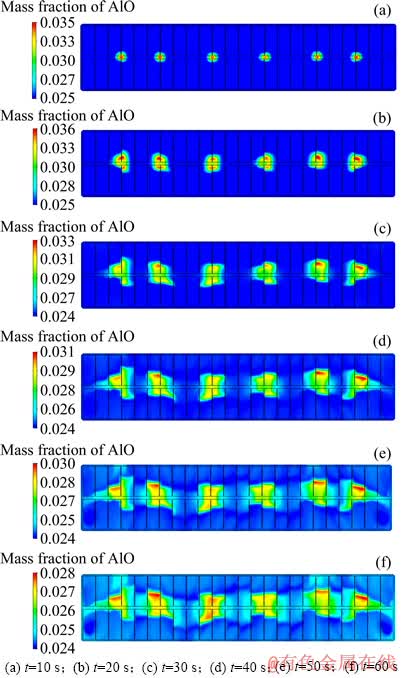
图5  全槽氧化铝浓度场在不同时间的瞬时分布

Fig. 5  Distribution of alumina concentration field of hole cell at different time

3  氧化铝传质过程的影响因素

氧化铝传质过程的动力学特征对氧化铝浓度分布变化有重要影响，对氧化铝传质过程的推动因素进行研究就成了必要。由式(3)所示的氧化铝传质方程可知，在铝电解槽操作工艺和工艺流程不变的前提下，质量源项不会发生改变，故影响氧化铝组分浓度的外部因素主要包括扩散项和对流项。研究发现，当电解质熔体停止运动时(即电解质不受到电磁力、阳极气泡的驱动时)，电解质内部对流作用很弱，氧化铝的传质仅靠自身的扩散。当下料200 s以后，发现氧化铝组分仍聚集在下料口正下方而没有分散，下料口正下方的氧化铝浓度很高而其他区域仍维持初始浓度不变。这表明扩散对氧化铝在电解槽中传质的贡献很小，可以忽略不计。因此，电解质熔体的对流才是促进氧化铝传质的最主要原因。

电磁力和阳极气泡的驱动是电解质熔体对流的主要因素，而且二者对熔体运动的影响各不相同。因此，采取单因素的研究方法即单一变量法，分别计算仅电磁力作用和仅阳极气泡作用下的全槽氧化铝浓度分布时变特征，探索二者在推动氧化铝输运从而达到全槽均匀分布这一过程中所起作用。

3.1  氧化铝传质过程中电磁力的影响作用

当仅存在电磁力作用时，不考虑阳极气泡相，计算得到电解质极间水平截面上氧化铝浓度最大值的时变情况如图6所示。

通过计算发现，仅存在电磁力作用时，氧化铝传质过程的动力学特征与电磁力、阳极气泡二者同时作用时截然不同。首先，在下料之后一段时间内，电解质极间区域的氧化铝浓度才显著上升，这表明电磁力作用下氧化铝从电解质表面向极距区的垂直输运较为缓慢；其次，氧化铝下料后聚集在较小的范围内，得不到很好地分散，最高浓度接近13%；再次，6个下料点附近的氧化铝浓度分布也有着明显的差别，最中间的2个下料点比外侧4个下料点附近的氧化铝浓度明显要低；最后，进电侧和出电侧的氧化铝浓度分布形态并不沿中缝对称，而是进电侧的浓度明显高于出电侧，这使得氧化铝更多地输运至进电侧。

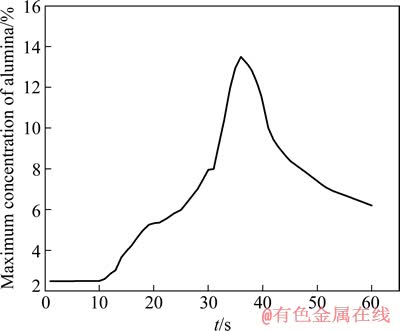
图6  仅存在电磁力作用时氧化铝浓度最大值时的时变

Fig. 6  Time varying at maximum concentration of alumina ratio when electromagnetic force working only

3.2  氧化铝传质过程中阳极气泡的影响作用

在忽略电磁力的影响仅阳极气泡作用的条件下，计算得到电解质极间水平截面上氧化铝浓度最大值变化情况，其结果如图7所示。

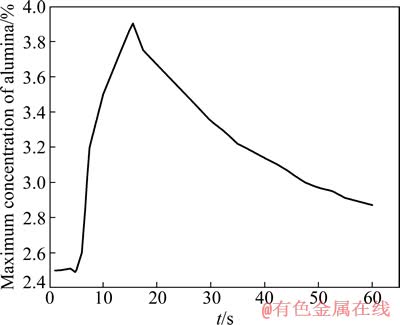
图7  仅阳极气泡作用时氧化铝浓度最大值时的时变

Fig. 7  Time varying at maximum concentration of alumina when anode bubble working only

同仅电磁力作用影响下的氧化铝浓度分布相比，仅阳极气泡作用下的全槽氧化铝浓度分布有着很好的对称性，进电侧与出电侧的浓度分布沿阳极中缝严格对称。同时，各个时刻的氧化铝浓度值均不高，最大氧化铝浓度在3.9%左右，低于仅电磁力作用下的氧化铝浓度最高值(约13%)，且稍低于二者同时作用下的情况。这表明阳极气泡下氧化铝能够较为迅速的分散。此外，各个下料点附近的氧化铝浓度分布形状差别不大。

由于阳极气泡主要从阳极底掌向四周逸出，其搅动作用也局限在阳极炭块附近，故在阳极气泡作用下，氧化铝并不能传质到较远的范围内，而是以阳极中缝为中心线，大多集中距离阳极中缝约二分之一个阳极宽度的区域内。

3.3  氧化铝传质与电解质环流运动的相互作用

综上分析，电磁力和阳极气泡对氧化铝输运过程影响的巨大差别，从本质上来说，是由二者对电解质环流运动(即涡流运动)的影响的差异性所决定的。

根据童秉纲等^[21]提出的涡流结构理论的解析结果，电磁力作用下的环流尺寸较大，但涡结构的对称性差，且涡的运动强度较弱，故这种情况下氧化铝能随着电解质的运动传质至槽内的各个区域，但氧化铝得不到熔体的快速搅动，其分散较慢，形成局部高浓度，且全槽浓度分布的差别很大，不沿阳极中缝对称。而阳极气泡作用时，涡流运动的强度很大，能迅速搅动氧化铝加快其分散过程，防止局部形成过高浓度。但是，阳极气泡的搅动范围仅局限在阳极炭块投影周围的有限空间内，涡流尺度较小，这无法推动氧化铝向槽内的广大区域输运，这与文献[22-23]的研究结论基本一致。

在生产实践中，要尽可能地加快铝电解槽中氧化铝的传质速度，使其及时溶解并分散至全槽；同时，要保证全槽氧化铝浓度的均匀性，杜绝局部氧化铝浓度过高的现象发生。

4  结论

1) 基于氧化铝传质过程的多组分多相流瞬态模型及数值计算方法，开展了500kA级特大铝电解槽内氧化铝传质的数值模拟计算，得到了500 kA电解槽内氧化铝浓度分布的时变情况。

2) 电解槽内氧化铝的浓度分布呈现周期性变化，下料后很短的时间内，在下料点正下方区域的氧化铝浓度急剧增加达到最大值3.9%；之后，氧化铝随着电解质流动不断分散，电解槽边缘区域的氧化铝浓度缓慢增加，而下料点正下方区域的氧化铝浓度缓慢下降，直至起始浓度2.8%附近。

3) 采用单一变量法研究电磁力和阳极气泡在氧化铝传质过程中作用，结果表明，仅电磁力作用下，氧化铝从电解质表面向极距的垂直输运较为缓慢，氧化铝聚集在下料点下方较小的区域；而仅在阳极气泡作用下，氧化铝能够较为迅速地分散，且各个下料点附近的氧化铝浓度分布形状差别不大。总体而言，阳极气泡对氧化铝传质的驱动作用比电磁力大，但范围没有电磁力广。

REFERENCES

[1] MOXNES B, SOLHEIM A, LIANE M, SVINSAS E, HALKJELSVIK A. Improved cell operation by redistribution of the alumina feeding[C]//BEARNE G. Light Metals 2009. San Francisco: TMS, 2009: 461-466.

[2] LI Jie, XU Yu-jie, ZHANG Hong-liang, LAI Yan-qing. An inhomogeneous three-phase model for the flow in aluminium reduction cells[J]. International Journal of Multiphase Flow, 2011, 37(1): 46-54.

[3] 徐宇杰. 铝电解槽内熔体运动数学建模及应用研究[D]. 长沙: 中南大学, 2010.

XU Yu-jie. A study of mathematical modeling and it’s application for the melts motion aluminium reduction cells[D]. Changsha: Central South University, 2010.

[4] 赵秋月, 张廷安. CFD技术在铝电解中的应用[J]. 轻金属, 2011, 12: 30-33.

ZHAO Qiu-yue, ZHANG Ting-an. Application of CFD technology in aluminum electrolysis[J]. Light Metals, 2011, 12: 30-33.

[5] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells[C]//HAGNIAM. Light Metals 2010. Seattle: TMS, 2010: 451-456.

[6] FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells[C]//LINDSAY J. Light Metals 2011. San Diego: TMS, 2011: 543-548.

[7] 夏小霞, 周乃君, 崔大光, 包生重. 156 kA 铝电解槽内电解质两相流动的数值模拟[J]. 中国有色金属学报, 2006, 16(11): 1988-1992.

XIA Xiao-xia, ZHOU Nai-jun, CUI Da-guang, BAO Sheng-zhong. Numerical simulation on two phase flow field of electrolyte in 156 kA aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(11): 1988-1992.

[8] 徐君莉, 石忠宁, 高炳亮, 邱竹贤. 氧化铝在熔融冰晶石中的溶解[J]. 东北大学学报: 自然科学版, 2003, 24(9): 832-834.

XU Jun-li, SHI zhong-ning, GAO Bing-liang, QIU Zhu-xian. Dissolution of alumina in molten cryolite[J]. Journal of Northeastern University: Natural Science, 2003, 24(9): 832-834.

[9] ROLSETH R, HOVLAND R, KOBBELTVEDT O. Alumina agglomeration and dissolution in cryolite melts[C]// MANNWEILER U. Light Metals 1994. San Francisco: TMS, 1994: 351-357.

[10] HAVERKAMP R G, WELCH B J. Modelling the dissolution of alumina powder in cryolite[J]. Chemical Engineering and Processing, 1998, 37: 177-187.

[11] LILLEBUEN B, BUGGE M, HOIE H. Alumina dissolution and current efficiency in Hall-Héroult cells[C]//BEARNE G. Light Metals 2009. San Francisco: TMS, 2009: 389-394.

[12] POI N W, HAVERKAMP R G, KUBLER S. Thermal effects associated with alumina feeding in aluminium reduction cells[C]//MANNWEILER U. Light Metals 1994. San Francisco: TMS, 1994: 219-225.

[13] BEREZIN A I, ISAEVA L A, BELOLIPETSKY V M. A model of dissolution and heating of alumina charged by point-feeding system in “virtual cell” program[C]//KVANDE H. Light Metals 2005. San Francisco: TMS, 2005: 151-154.

[14] BLATCH G I, TAYLOR M P. Computer simulation of the replacement of pre-bake anode in an aluminium reduction cell[C]//Australia’s Bicentennial international conference for the process industries, 1988: 13-20.

[15] von KAENEL R, ANTILLE J, ROMERIO M, BESSON O. Impact of magnetohydrodynamic and bubbles driving forces on the alumina concentration in the bath of an Hall-Héroult cell[C]// ARRY S. Light Metals 2013. San Antonio: TMS, 2013: 585-590.

[16] 徐 宁, 杨振海, 邱竹贤. 氧化铝在冰晶石熔体中溶解的动力学模型 [J]. 东北大学学报: 自然科学版, 1996, 20(3): 315-318.

XU Ning, YANG Zheng-hai,QIU Zhu-xian,CHENG Tao. Kinetic model of dissolution of alumina in molten cryolite[J]. Journal of Northeastern University: Natural Science, 1996, 20(3): 315-318.

[17] 张家奇. 基于数学模型的铝电解槽动态过程及其预报系统研究[D]. 长沙: 中南大学, 2011.

ZHANG Jia-qi. Principal electrolysis processes and corresponding prediction system for aluminum electrolysis cells based on mathematical models[D]. Changsha: Central South University, 2011.

[18] 冯乃祥. 铝电解[M]. 北京: 化学工业出版社, 2006, 196-205.

FENG Nai-xiang. Aluminum electrolysis[M]. Beijing: Chemical Industry Press, 2006: 196-205.

[19] THONSTAND J, ROLSETH S. The electrode reaction on the C, CO₂ electrode in cryolite-alumina melts[J]. Electrochimica Acta, 1978, 23: 233-241.

[20] STERTEN A, SOLLI P A. An electrochemical current efficiency model for aluminium electrolysis cells[J]. Journal of Applied Electrochemistry, 1996, 26: 187-193.

[21] 童秉纲, 尹协远, 朱克勤. 涡运动理论[M]. 合肥: 中国科学技术大学出版社, 1994: 121-136.

TONG Bing-gang, YIN Xie-yuan, ZHU Ke-qing. The theory of eddy motion[M]. Hefei: University of Science and Technology of China Press, 1994: 121-136.

[22] 李 劼, 张翮辉, 张红亮, 徐宇杰, 杨 帅, 赖延清. 大型铝电解槽电解质流场涡结构的数值模拟[J]. 中国有色金属学报, 2012, 22(7): 2082-2089.

LI Jie, ZHANG He-hui, ZHANG Hong-liang, XU Yu-jie, YANG Shuai, LAI Yan-qing. Numerical simulation on vortical structures of electrolyte now field in large aluminium reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(7): 2082-2089.

[23] 詹水清, 李 茂, 周孑民, 周益文, 杨建红. 铝电解槽熔体内氧化铝浓度分布的数值模拟[J]. 中国有色金属学报, 2014, 24(10): 2658-2667.

ZHAN Shui-qing, LI Mao, ZHOU Jie-min, ZHOU Yi-wen, YANG Jian-hong. Numerical simulation of alumina concentration distribution in melts of aluminum reduction cells[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2658-2667.

(编辑  王  超)

基金项目：国家自然科学基金资助项目(51104187，51274241，51264011)；国家自然科学创新研究群体科学基金资助项目(61321003)

收稿日期：2014-07-13；修订日期：2014-12-15

通信作者：张红亮，副教授，博士；电话：0731-88830474；E-mail：net_hotang@163.com