基于小波和Wigner-Ville分布的轨道不平顺特征识别
徐磊1, 2,陈宪麦1, 2,徐伟昌3,彭欣1
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 高速铁路建造技术国家工程实验室,湖南 长沙,410075;
3. 上海铁路局工务处,上海,200070)
摘要:利用小波变换的多分辨特性,对轨道不平顺局部检测数据进行一维小波变换多尺度分解,然后对各尺度下重构信号进行幅值谱分析,以发现在轨道不平顺中存在的特征不利波长;同时,基于小波分解后的各层重构信号能有效放大不平顺特征和缩小频段范围,利用Wigner-Ville分布对信号能量的时频聚集性,对各层重构信号进行Wigner-Ville时频分析能很好地提取各波长不平顺大小沿线路里程的分布情况;通过相干分析发现引起车体激扰的不利波长,然后用小波方法提取不利波长所在的特征频段,最后通过互Wigner-Ville分布表征相干不利波长不平顺的时-频分布情况。结果表明:结合小波分析理论和Wigner-Ville分布能十分有效地从时-频域角度分析轨道不平顺,是一条保证铁路安全运营、提高养护维修质量的良好技术途径。
关键词:轨道不平顺;小波;Wigner-Ville分布;相干分析;特征识别
中图分类号:U213.2 文献标志码:A 文章编号:1672-7207(2013)08-3344-07
Explored of track irregularity’s characteristic identification based on wavelet method and Wigner-Ville distribution
XU Lei1, 2, CHEN Xianmai1, 2, XU Weichang3, PENG Xin1
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;
3. Shanghai Railway Bureau Works Department, Shanghai 200070, China)
Abstract: By exploiting the multiresolution characteristic of wavelet transform, we can put the local testing data into multiscale decomposition through 1D wavelet transform, and then analyse the reconstructing signal of each scale using the amplitude spectrum to find the feature unfavorable wavelength existed in the track irregularity; At the same time, we can reduce the cross distraction of the Wigner-Ville distribution based on the fact that the wavelet decomposition can effectively magnify the characteristic of the irregularity and narrow the frequency band, through using the Wigner-Ville distribution which can draw the time-frequency clustering of the signal energy; Finding the unfavorable wavelength that causes the car-body vibration, then extracting the feature frequency band of the unfavorable wavelength, at last, we can finally represent the time-frequency distribution condition of cross unfavorable wavelength through the method of cross Wigner-Ville distribution. The result shows that we can effectively analyse the track irregularity from the time-frequecy domain through combining wavelet method and Wigneer-Ville distribution. It’s a new technical method for guaranteeing the safe running of railway and improving the maintenance quality.
Key words: track irregularity; wavelet; Wigner-Ville distribution; coherence analysis; characteristic identification
小波变换具有带通滤波器的作用和多分辨率分析的特点,可以由粗到细的逐渐观察信号[1],只要适当的选择基本小波,通过小波的多尺度分析可将信号分解为反映信号整体趋势的低频部分和反应信号细节的高频部分,就可以在时、频域很好的表征信号的局部特征,常用的小波基函数如有Morlet,Marr,Harr和Dubechies等。基于这些优点,小波变换已在数字图像处理、故障诊断、语音和生物医学信号处理及光谱分析等方面获得广泛的应用[2-3]。但另一方面,小波变换在本质上属于线性时频表示,不能描述信号的瞬时功率谱密度。二次型时频分布是一种更加直观和合理的信号表示方法[1],Wigner-Ville分布(WVD)就是一种重要的二次型时-频信号分布, Wigner将其提出并最初应用于量子力学的研究。Ville将其引入信号分析领域。20世纪60年代中期,Cohen发现众多的时频分布只是Wigner-Ville分布的变形。此后一些学者对Wigner-Ville分布做了进一步的分析研究,并给出了这种变换的数学基础和重要数学性质[4-5]。在处理信号,尤其是处理非平稳信号中发挥了巨大的作用。现有的谱密度计算方法,如FFT法、最大熵等方法,都是建立在平稳性假定的基础上的[6],基于多数轨道不平顺样本记录具有平稳性或弱平稳特征,可以近似将其作为平稳随机过程来处理。但在接头焊缝、道岔区、各种轨道病害地段的不平顺,往往具有非平稳特征。为了能从时-频域角度较好地诊断轨道不平顺病害,发现轨道不平顺不利波长特征,本文作者利用小波变换具有的多分辨率分析的特点,对京沪高铁各单项不平顺轨检数据进行一维小波变换多尺度分解,对各区段不平顺幅值分波段进行分离,然后进行幅值谱分析,分析不利波长。同时利用Wigner-Ville分布具有时频聚集性及其能很好的描述信号能量密度分布的特性,对各尺度下的小波重构信号进行Wigner-Ville时频分析。由此提取小波变换各尺度下功率谱图的波幅信息和Wigner-Ville分布中信号能量的时间-频率信息,获得轨道随机不平顺的时间-频率-幅值三维分布特征,为提高工务部门的线路维修养护质量提供新的技术支持。
1 小波变换[7]
小波是具有震荡特性、能够迅速衰减到0的一类函数,即 。由
。由 的伸缩和平移构成一簇函数系:
的伸缩和平移构成一簇函数系:
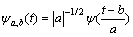 ,
,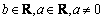 (1)
(1)
式中,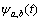 称为子小波;a为尺度因子或频率因子;b为时间因子或平移因子。对于离散信号
称为子小波;a为尺度因子或频率因子;b为时间因子或平移因子。对于离散信号
 (i=1,2,…,N;N为样本容量;△t为取样时间间隔),离散小波变换定义为:
(i=1,2,…,N;N为样本容量;△t为取样时间间隔),离散小波变换定义为:
 (2)
(2)
Wf(a,b)包含了f(t)和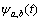 的信息,所以小波函数的选择十分重要,本文尝试了多种小波函数,结果显示Dubechies小波对本研究具有较好的性能。
的信息,所以小波函数的选择十分重要,本文尝试了多种小波函数,结果显示Dubechies小波对本研究具有较好的性能。
2 Wigner-Ville分布
2.1 定义及性质
双线性时间-频率分布具有较高的时频分辨率和一定的噪声抑制能力已广泛应用于非平稳信号处理及瞬时信号检测中[8],信号s(t)的Wigner-Ville分布定义为[1]:
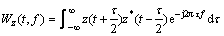 (3)
(3)
式中:z(t)为s(t)的解析信号,z*为z的共轭。
 (4)
(4)
式中:s(t)为z(t)的实部,虚部为s(t)的Hilbert变换。
信号s1(t)和s2(t)的互Wigner-Ville分布定义为
 (5)
(5)
Wigner-Ville分布最重要的性质之一就是具有明确的物理意义,可被看作信号能量在时频域的分布,并且在求解信号的Wigner分布时,不会损失信号的幅值和相位信息。它还具有实值性、对称性、时-频移不变性和时-频边缘特性等重要性质。
2.2 Wigner-Ville分布中的交叉项问题[1, 9]
对于多分量信号,根据卷积定理,Wigner-Ville分布会出现交叉项,产生“虚假信号”。交叉项是二次型时频分布的固有结果,它来自多分量信号中不同信号分量之间的交叉作用。假设x(t)=ax1(t)+bx2(t),记x(t),x1(t),x2(t)的线性时频表示分别为P(t,f),P1(t,f),P2(t,f),则有
 (6)
(6)
式中:最后一项即为干扰项,这是二次型时频表示固有的一个属性。
目前对交叉项的抑制主要通过加窗平滑的方法来实现,即伪WVD,其表达式为:
 (7)
(7)
式中:y(t)为窗函数。
结合本文研究目的,采用平滑伪Wigner-Ville分布对轨道不平顺样本数据进行时频分析。
3 基于小波分解的不平顺频谱特征分析
3.1 样本来源
采用样本数据来源于轨道检查车2010年07月检测的京沪高铁线的检测数据,采样里程为220.9 km,数据采样间距为0.25 m。
3.2 基于小波分解的频谱分析
轨道不平顺是一个随机波形,它包含多种波形成分,在总的轨道谱中,由于各种波形的相互影响,可有些波可能观察不到,甚至会出现相互抵消的情况。通过小波分解,将轨道不平顺分解到各个逼近信号和细节信号,再对这些分解信号进行功率谱分析[10],可以更好的识别。本文利用一维离散小波变换进行信号处理,小波算法用mallet算法实现[11],采用Daubechies6小波基对轨道左高低不平顺实施小波分解。
小波分解的高频部分代表信号的细节项,低频部分代表信号的趋势项,分解的层数应该由采样频率和所关注的重点频率共同确定[12]。针对本文采用的数据,并结合采样定理以及Mallat算法在各子频带上的频率范围,最终确定小波分解的层数为6层。
具体求解过程如下:
(1) 令x(i)(i=1,2,…,n)为轨检车检测的单项不平顺数据,n为检测点数。
(2) 取x(i)中对应研究区段不平顺数据进行小波分解,得到aj(i)和dj(i)(j=1,2,…,k),k为小波分解层数。a(i)为x(i)低频小波系数,d(i)为x(i)高频小波系数。
(3) 对各层aj(i)和dj(i)分别进行小波系数重构,得到小波处理后各单项不平顺的波段信号aj(i)和dj(i)。
(4) 对aj(i)和dj(i)进行FFT变换,计算相应幅值谱,并进行分析。
本文取京沪高铁k2.5+0~k2.5+1.024为研究区段,其左高低不平顺小波分解后各层近似信号和细节信号的不平顺幅值谱见图1和2。
分析图1和2可知:细节信号幅值谱基本上在整个不平顺波动范围都有幅值分布,信号a(1),a(2)和d(4)集中反映了32~33 m波长处和6.5 m波长附近的周期性不平顺,表现得非常显著,32~33 m波长不平顺在a(4),a(5)和a(6)中也有所体现,表明其为较不利波长;而细节信号谱随层数的变化,其所分析的波段范围产生了频移。从d(1)~d(6),频段逐渐向低频移动,各层细节信号都将其所在波段不平顺特征清楚地反映出来,如d(1)主要反映了波长1~2 m的不平顺信号,其谱线含有窄带随机波和复杂周期性波特征,在1.1~1.6 m窄带范围存在十分显著的尖峰波长;分析d(2),d(3)和d(4),其谱曲线中都存在十分显著的周期性尖峰波长,如1.53,2.88和6.48 m等,同时发现在近似信号中普遍存在的32~33 m周期性波长在细节信号中不能很好地体现出来,这是因为细节信号主要用于不平顺中的高频信号,其幅值一般要较近似信号为低,而对于如32 m等长波长,其幅值较高,故不能很好地在细节信号得以体现。但细节信号在处理中短波长不平顺时,可以“放大”轨道不平顺特征[10],更好地提取特征不平顺,故其也有不可忽视的作用。
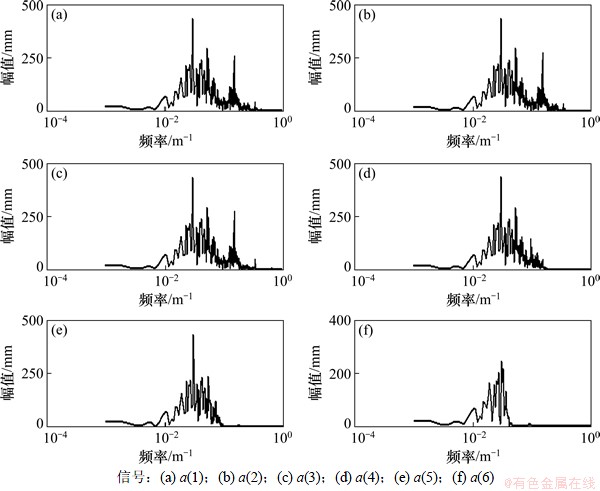
图1 近似信号幅值谱
Fig. 1 Amplitude spectrum of approximate signal
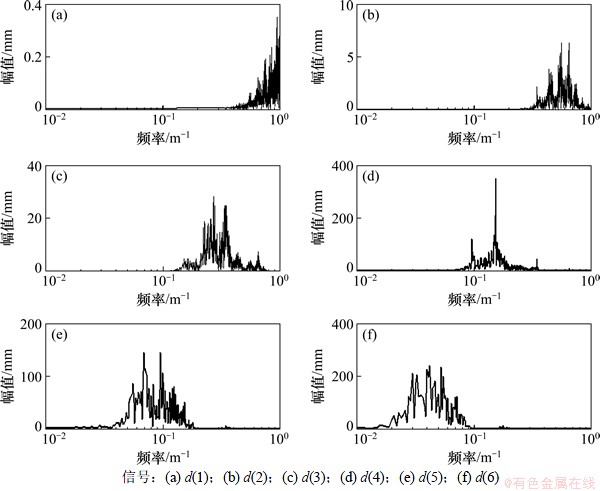
图2 细节信号幅值谱
Fig. 2 Amplitude spectrum of detail signal
4 基于Wigner-Ville分布的不平顺时-频分析
4.1 Wigner-Ville分布与小波分解信号的互识
小波分解后的各层重构信号较原始信号的频率成分单一,其幅值能量分布更为集中,在 Wigner-Ville分布中能得以更好体现。图3和4分别为d(2),d(4)重构信号及其Wigner-Ville分布时频。
分析图3和4可以发现:在小波重构信号幅值波动较大,并且呈现高频振动状态的区段,与之对应的Wigner-Ville分布中时域面也出现能量集中的情况,如在细节信号d(4)中,k2.5+0.197~k2.5+0.217和k2.5+0.516~k2.5+0.529等区段幅值波动较大,其所对应的Wigner-Ville分布相应区段的能量也集中分布;在d(2)信号中也有同样的情况。而在频域分布中,分析图3中的Wigner-Ville分布可以发现,d(2)的能量主要分布在频段0.45~0.69 m-1,特别是在频段0.54~0.57 m-1和0.61~0.67 m-1能量很大,由图2所示d(2)幅值谱可以发现,其幅值分布范围主要在0.43~0.70 m-1之间,窄带尖峰波长集中在0.43~0.47,0.53~0.567和0.63~0.66 m-1等波段,说明Wigner-Ville分布也能较好的表征能量在频域内的分布情况。图5和6所示为d(2)和d(4)在时频面上的能量分布。
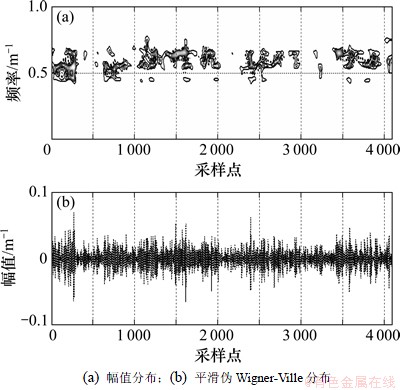
图3 d(2)幅值分布(a)及其平滑伪Wigner-Ville分布(b)
Fig. 3 Distribution of d(2)’s amplitude and it’s SPWVD

图4 d(4)幅值分布(a)及其平滑伪Wigner-Ville分布(b)
Fig. 4 Distribution of d(4)’s amplitude and it’s SPWVD
从图5和6可以看出:小波分解后的不平顺信号能量分布较为集中,其Wigner-Ville分布能够很好识别轨道不平顺的时-频分布特征。各小波重构信号的Wigner-Ville分布中的时频分布能量峰对应的就是轨道不平顺最不利位置。
图7和8所示为京沪高铁k2.5+0~k2.5+1.024研究区段原始左高低轨检数据的Wigner-Ville分布。
从图7和8分析可知:原始数据的Wigner-Ville分布能较好的表征不平顺中存在的幅值较大的周期性波长,如6.5 m和32~33 m波长不平顺,但对于其他幅值较小的不利波长则不能很好地得以表达。所以,结合小波分解后的各层重构信号进行Wigner-Ville分布时-频分析,能取得更好的效果。

图5 d(2) Wigner-Ville分布三维图
Fig. 5 Three dimension WVD of d(2)

图6 d(4)Wigner-Ville分布三维图
Fig. 6 Three dimension WVD of d(4)

图7 Wigner-Ville分布(等高线)
Fig. 7 WVD (contour line)

图8 Wigner-Ville分布(三维图)
Fig. 8 WVD (three-dimensional Graph)
4.2 基于相干分析和互Wigner-Ville分布的不利波长时-频分析
利用相干理论[13]可对轨道不平顺与车辆振动加速度进行分析,研究车辆的振动与轨道不平顺的相干程度,以此来确定对车辆振动的影响最大的不平顺波长范围及类型。输入输出之间的相关性用常相干函数来分析,平稳随机信号y(t)和x(t)之间的相干函数定义为
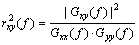 (8)
(8)
式中:Gxx(f),Gyy(f)分别为x(t)和y(t)的单边自功率谱,Gxy(f)为Gxx(f)和Gyy(f)的单边互功率谱密度函数。 越大表示x(t)和y(t)的相干性越强。
越大表示x(t)和y(t)的相干性越强。
但相干分析只能确定引起车辆振动的最不利波长,而无法确定不利波长的时域分布范围。如果结合Wigner-Ville分布良好的时频分析能力,则能在相干分析初步确定不利波长的基础上,通过小波方法细化其不利波段范围,结合互Wigner-Ville分析,确定轨道不平顺对车体振动影响沿线路里程的分布情况。其主要步骤如下:
(1) 对所要分析的单项不平顺和车体振动类型进行相干分析,确定最不利波长或其范围,这里以左高低不平顺和车体垂向振动加速度为例。
(2) 依据最不利波长和采样频率,针对性的确定小波分解层数,然后对左高低不平顺和车体垂向振动加速度数据实行小波分解,并进行小波系数重构。
(3) 提取左高低不平顺和车体垂向振动加速度相干不利波长所在的小波重构信号,对其进行互Wigner-Ville分布时-频分析。
(4) 分析不利波长能量沿线路里程的分布情况,发现存在病害。
以京沪高铁k2.5+0~k2.5+1.024为研究区段。图9(a)~(c)所示为轨道左高低不平顺和车体垂向加速度的相干函数,以及代表性不利波长重构信号的互Wigner-Ville分布三维图。
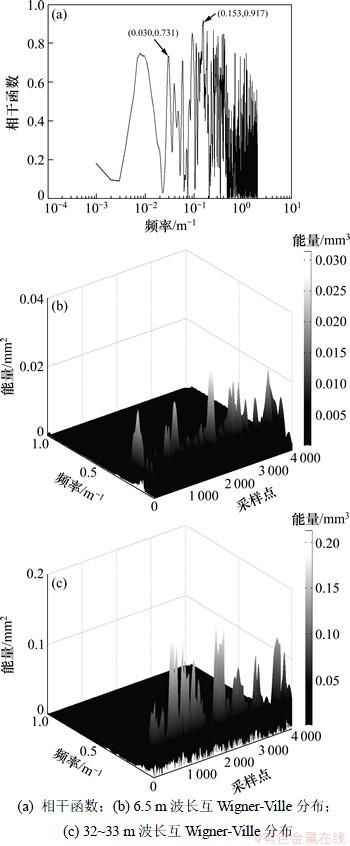
图9 k2.5+0~k2.5+1.024段不利波长时-频分布
Fig. 9 Time-frequency distribution graph of unfavorable wavelength in sector k2.5~k2.5+1.024
从图9(b)和(c)可见:沿线路里程引起车体垂向振动的轨道高低不平顺相干不利波长主要分布在6.5 m和32~33 m波长(段),与图9(a)基于相干理论得出的车体振动最不利波长一致。分析图9(b),在6.5 m高低不平顺波长影响下,在采样点1756~1764处(对应里程:k2.5+439~ k2.5+441)车体垂向激振能量极为显著,说明此路段在6.5m波长下容易引起车辆激扰,需要重点管理;同理,图9(c)所示,在采样点658~682处(对应里程:k2.5+164.5~ k2.5+170.5)和采样点1874~2016处(对应里程:k2.5+468.5~ k2.5+504)为容易引起车体垂向振动的不平顺恶劣路段,要重点监测其不平顺状况,并加强其养护维修。
5 结论
(1) 通过小波分解,可以识别不同波长范围内突出的特征不平顺,并可以提取这些不平顺进行深入研究。
(2) 由于轨道不平顺在不同波长处,其幅值相差很大,所以直接对轨检数据进行Wigner-Ville分布时-频分析无法取得很好的效果。而通过小波方法对各单项不平顺进行多尺度分解重构,可以放大波幅特征和缩小分析频段范围,研究结果表明,基于重构信号的Wigner-Ville分析方法能达到很好的不平顺时-频分析效果。
(3) 通过相干分析提取引起车辆振动激扰不平顺不利波长,在此基础上,结合小波方法和Wigner-Ville分布能有效提取引起车辆激振的不利路段,从而为工务部门及时查找并发现病害、提高养护维修质量及保证铁路安全运营提供了新的技术途径。
参考文献:
[1] 葛哲学, 陈仲生. 时频分析技术及其应用[M]. 北京: 人民邮电出版社, 2006: 1-9.
GE Zhexue, CHEN Zhongsheng. Time-frequency analysis technology and its application[M]. Beijing: Posts & Telecom Press, 2006: 1-9.
[2] 张亭禄, 杜祥之, 徐青娜, 等. 一维小波分析在浮游植物吸收光谱有害赤潮藻类检测中的应用[J]. 光谱学与光谱分析, 2009, 29(10): 2743-2747.
ZHANG Tinglu, DU Xiangzhi, XU Qingna, et al. Application of 1D wavelet analysis in detecting species of harmful algae blooms with absorption spectra of phytoplankton[J]. Spectroscopy and Spectral Analysis, 2009, 29(10): 2743-2747.
[3] 杜灿谊, 杨志坚, 丁康. 小波分析在发动机失火监测中的应用[J]. 振动、测试与诊断, 2011, 31(3): 318-322.
DU Canyi, YANG Zhijian, DING Kang. The Application of Wavelet analysis in engine fire monitoring[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3): 318-322.
[4] Classen T C M, Mecklenbrauker W F G. The Wigner distribution-a tool for time-frequency signal analysis, part I: Continuous-time signals[J]. Philips Journal of Research, 1980, 35(3): 217-250.
[5] Classen T C M, Mecklenbrauker W F G. The Wigner distribution-a tool for time-frequency signal analysis, part II: Discrete-time signals[J]. Philips Journal of Research, 1980, 35(4/51): 276-300.
[6] 罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态的控制[M]. 北京: 中国铁道出版社, 2006: 174.
LUO Lin, ZHANG Geming, WU Wangqing, et al. The control of the state of track regularity in wheel-rail system[M]. Beijing: China Railway Publishing House, 2006: 174.
[7] 王文圣, 丁晶, 向红莲. 小波分析在水文学中的应用研究及展望[J]. 水科学进展, 2002, 13(4): 515-520.
WANG Wensheng, DING Jing, XIANG Honglian. Application and prospect of wavelet analysis in hydrology[J]. Advances in water science, 2002, 13(4): 515-520.
[8] 马瑞恒, 王新晴. 基于一种新的时频分布的机械故障诊断[J]. 振动与冲击, 2003, 22(3): 68-74.
MA Ruiheng, WANG Xinqing. The mechanical failure diagnosis based on a new time-frequency distribution[J]. Journal of Vibration and Shock, 2003, 22(3): 68-74.
[9] 石小羊, 吴天佑. 基于时频重排的地震信号Wigner-Ville分布时频分析[J]. 石油地球物理勘探, 2009, 42(2): 201-205.
SHI Xiaoyang, WU Tianyou. The seismic signals analysis based on the time-frequency rearrangement Wigner-Ville distribution[J]. Oil Geophysical Prospecting, 2009, 42(2): 201-205.
[10] 陈宪麦, 王澜, 陶夏新, 等. 基于小波分析理论的轨道不平顺分析[J]. 铁道工程学报, 2008, 1(1): 57-61.
CHEN Xianmai, WANG Lan, TAO Xiaxin, et al. Analysis of track irregularity with wavelet theory[J]. Journal of Railway Engineering Society, 2008, 1(1): 57-61.
[11] 程振兴. 小波分析算法和应用[M]. 陕西: 西安交通大学出版社, 1998: 45-57.
CHEN Zhenxin. Wavelet analysis algorithm and application[M]. Shaanxi: Xi’an Jiaotong University Press, 1988: 45-57.
[12] 曲铭, 许玉德. 基于小波的列车加速度和轨道不平顺关系分析[J]. 华东交通大学学报, 2008, 25(5): 36-41.
QU Ming, XU Yude. An analysis of the relationship of acceleration and track irregularity based on wavelet[J]. Journal of East China Jiaotong University, 2008, 25(5): 36-41.
[13] 安木金, 李舜铭, 张袁元. 多相干子系统输入中输入的相干性分析[J]. 中国机械工程, 2010, 21(21): 2609-2613.
AN Mujin, LI Shunming, ZHANG Yuanyuan. Coherence analysis of inputs using multiple correlated subsystem-inputs system modeling[J]. China Mechanic Engineering, 2010, 21(21): 2609-2613.
(编辑 陈爱华)
收稿日期:2012-10-09;修回日期:2012-12-15
基金项目:国家自然科学基金资助项目(51008315);中南大学研究生自主探索创新项目(2013zzts233);上海铁路局科研项目(2013072)
通信作者:陈宪麦(1975-),男,甘肃会宁人,副教授,从事线路平顺性、养护维修领域的研究;电话:13549665210;E-mail:xianmaichen@aliyun.com