DOI: 10.11817/j.issn.1672-7207.2021.04.034
基于改进磁链峰值能量法的牵引电机轴承故障诊断
冯江华
(中车株洲电力机车研究所有限公司,湖南 株洲,412001)
摘要:基于电信号轴承故障诊断机理,提出一种基于改进磁链峰值能量法的牵引电机轴承故障诊断方法,并开展了轴承故障模拟试验和现场案例验证。首先,以采集获得的电机电流、转速以及重构电压信号作为输入,采用牵引电机全阶磁链观测器计算获得磁链信号;其次,采用快速峭度谱算法对磁链信号进行自适应滤波,消除背景噪声、低频基频及其谐波等干扰信号的影响,对滤波后的磁链信号进行峰值平方整流和包络解调处理,进一步计算磁链峰值能量法;最后,提取磁链峰值能量法中的轴承故障特征分量,实现诊断轴承故障。研究结果表明:本文所提出的方法能够有效地提取轴承故障微弱特征信号,可实现对牵引电机轴承外圈、内圈和滚动体等故障部位的精确诊断。
关键词:牵引电机;轴承;故障诊断;磁链观测器;峰值能量
中图分类号:U264.1 文献标志码:A
文章编号:1672-7207(2021)04-1380-09
Fault diagnosis of traction motor bearing based on improved flux peak energy method
FENG Jianghua
(CRRC Zhuzhou Institute of Electric Locomotive, Co. Ltd., Zhuzhou 412001, China)
Abstract: On the basis of the motor bearing fault characterized in the mechanism model of electrical signals, a traction motor bearing fault diagnosis method based on improved flux linkage peak energy method was proposed, and bearing fault simulation tests and field case verification were carried out. Firstly, the collected motor current, motor speed and reconstructed voltage signal were taken as input, and the full-order flux linkage observer of the traction motor was used to calculate the flux linkage signal. Secondly, an adaptive filtering algorithm based on fast kurtosis spectrum was used to filter the flux linkage signal, which will eliminate the effects of interference signals such as background noise, low-frequency fundamental frequency and its harmonics. Square rectification and envelope demodulation was exploited to process the filtered flux linkage signal, and the flux peak energy spectrum was calculated. Finally, diagnose bearing faults by extracting the characteristic components of bearing faults in the peak energy spectrum of flux linkage was diagnosed. The results show that the method proposed in this paper can effectively extract the weak characteristic signals of bearing faults, and can realize the accurate diagnosis of the fault position such as the outer ring, inner ring and rolling elements of the traction motor bearings.
Key words: traction motor; bearing; fault diagnosis; flux linkage observer; peak energy
牵引电机作为驱动列车高速运行的主要部件之一,实现机-电能量相互转换与传递,对列车安全、可靠和稳定运行起着至关重要作用。在轨道交通特有运行环境下,牵引电机受温湿度、负载冲击和工况转换等复杂运行环境的影响,在电、磁、热和力等复合交变载荷长期作用下,其轴承性能存在退化和疲劳损伤,影响列车平稳运行,严重时会造成电机锁轴,拉伤轨道,甚至导致列车脱轨。实现轨道交通复杂运行工况下牵引电机轴承故障的精准诊断,具有极大的工程应用和社会经济价值。目前,电机轴承故障诊断技术主要有2类方法,即振动分析法[1-2]和电信号分析法[3-4]。受列车高速运行的影响,振动信号呈现出非平稳性[5]和非高斯性等特征[6],故障特征信号微弱且容易受到外界因素的影响,从而导致漏报率和误报率较高;同时,该方法新加装的振动加速度传感器等监测设备的可靠性及使用寿命难以达到轨道车辆的要求,导致出现更高的故障率。电信号分析法是一种非侵入式的轴承故障诊断法,基于已有控制信号完成诊断,不需要额外增加传感器,具有易于工程化实施的优点。这类方法主要是通过转速、转矩[7]和电流[8]等电气参数进行频谱分析,进一步提取轴承故障特征分量,研究最为广泛的是基于电流信号的故障诊断方法[9-11]。然而,由于牵引电机是PWM(pulse width modulation)变频供电,受到调速复杂工况等的影响,牵引电机电流谐波相对于定频、正弦波供电的工业电机而言,谐波成分更加丰富,轴承故障微弱特征分量容易被电流基频谐波等强背景噪声淹没,这增加了电流分析的难度,传统方法难以有效识别出牵引电机电流中的轴承故障特征分量。为此,本文作者在分析基于电信号轴承故障诊断机理的基础上,提出一种改进磁链峰值能量法的牵引电机轴承故障诊断方法。首先,建立牵引电机全阶磁链观测器模型,根据电机三相电流、转速等信号实时计算磁链;其次,对磁链信号进行峰值平方整流和包络解调处理,进一步计算磁链峰值能量法;最后,通过提取轴承故障特征分量实现轴承故障诊断。此外,开展了故障模拟试验与现场应用案例验证。
1 电机轴承故障机理
当电机发生轴承故障时,滚动体每次经过故障点时会引起感应电机转子径向位移[12],导致感应电机定转子之间的气隙长度发生变化,这种变化将会影响磁导,引起电机磁链产生一种周期性脉冲。具体故障机理如下。
根据轴承外圈固定的电机结构,BLODT等[13]提出了轴承故障状态下的气隙偏心模型,即当滚动体经过故障点时,电机气隙长度将发生短暂的静态偏心。假设电机轴承正常,且不考虑定转子开槽的影响,此时,在定转子完全对中状态下气隙长度为定常数 。相对地,当轴承发生缺陷且滚动体每次经过缺陷点时,气隙长度可以近似地表示为
。相对地,当轴承发生缺陷且滚动体每次经过缺陷点时,气隙长度可以近似地表示为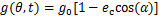 。其中,
。其中,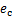 为定转子相对偏心率,这将导致气隙动态偏心,此时,气隙长度可表示为
为定转子相对偏心率,这将导致气隙动态偏心,此时,气隙长度可表示为
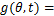
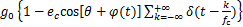 (1)
(1)
式中: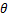 为定子参考坐标系下的轴承缺陷的初始相位;
为定子参考坐标系下的轴承缺陷的初始相位;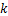 为整数;
为整数;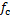 为对应轴承缺陷位置的通过频率,其表达式如下:
为对应轴承缺陷位置的通过频率,其表达式如下:
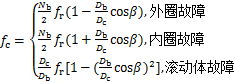 (2)
(2)
式中: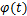 为滚动体与轴承缺陷接触时的角相位[13]:
为滚动体与轴承缺陷接触时的角相位[13]:
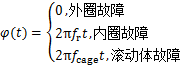 (3)
(3)
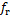 为转子旋转角频率;
为转子旋转角频率;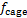 为保持架旋转角频率;
为保持架旋转角频率;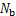 为滚动体个数;
为滚动体个数;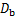 为滚动体直径;
为滚动体直径;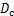 为轴承中径;
为轴承中径;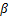 为滚动体接触角。
为滚动体接触角。
以外圈缺陷为例进行说明,外圈缺陷一般发生在电机承载区位置,因此,参考坐标系可选择承载区为坐标零相位点。此时,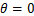 ,
,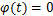 ,滚动体每次经过外圈缺陷点将会引起气隙长度变化,如图1所示。在定转速下滚动体经过外圈是等周期的,其周期为
,滚动体每次经过外圈缺陷点将会引起气隙长度变化,如图1所示。在定转速下滚动体经过外圈是等周期的,其周期为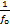 ,其中,
,其中, 对应式(2)中考虑外圈情况时
对应式(2)中考虑外圈情况时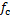 的定义,为滚动体相对外圈的通过频率,则气隙长度变化也是等周期,如图2所示。
的定义,为滚动体相对外圈的通过频率,则气隙长度变化也是等周期,如图2所示。

图1 轴承缺陷引起转子径向位移
Fig. 1 Bearing defects cause rotor radial displacement
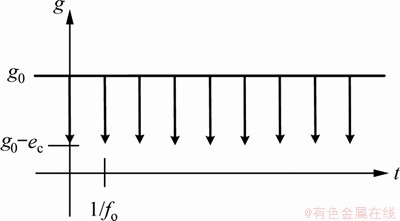
图2 气隙长度变化规律
Fig. 2 Air gap length variation law
由于磁导与气隙长度呈反比,则轴承故障时,磁导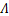 可以表达式为
可以表达式为
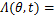
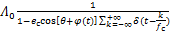 (4)
(4)
式中: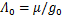 ,为无偏心状态下电机气隙磁导;
,为无偏心状态下电机气隙磁导;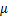 为气隙磁导率。
为气隙磁导率。
对式(4)进行傅里叶分解可得磁导的简化表达式[14-16]:
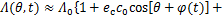

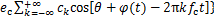 (5)
(5)
式中: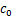 和
和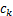 为傅里叶奇数系数。
为傅里叶奇数系数。
当只考虑驱动电源中的基频磁动势的影响时,感应电机的总磁动势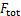 可以表示为
可以表示为
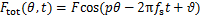 (6)
(6)
式中: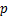 为电机极对数;
为电机极对数;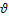 为电机转子位置的初始角度;F为磁动势基频幅值。
为电机转子位置的初始角度;F为磁动势基频幅值。
据式(5)和式(6),可得磁通密度的表达式:
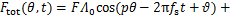
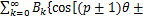
 (7)
(7)
式中: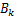 为磁通密度的幅值;
为磁通密度的幅值;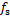 为电机电流基频。
为电机电流基频。
此时,磁链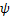 则可用磁通密度为
则可用磁通密度为
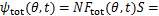
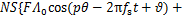
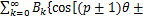
 (8)
(8)
式中: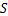 为磁场面积;
为磁场面积;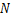 为线圈匝数。
为线圈匝数。
从式(8)可知,由轴承故障引起的转子偏心将作用在电机磁链上,即磁链包含因轴承故障导致的特定故障频率分量,这种特定的故障频率分量可表达为
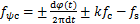 (9)
(9)
将式(2)和式(3)代入式(9),则可得到磁链中的轴承故障特征分量:
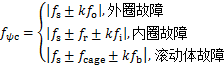 (10)
(10)
式中: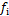 和
和 分别对应式(2)中考虑内圈和滚动体情况下的通过频率。
分别对应式(2)中考虑内圈和滚动体情况下的通过频率。
2 改进峰值能量法
峰值能量法是由Emerson公司提出的一项新型信号采集与处理技术,它用于解调机械设备激励出的周期性冲击信号,可以有效检测出轴承和齿轮箱故障[17]。相对于传统共振解调法,它能够发现故障初期潜在的低能量异常信号,从而能够准确地反映故障根源及其严重程度。改进峰值能量法的优化及实现过程具体如下。
1) 选择合适的滤波器。一般选择高通或者带通滤波器,将机械正常运转的低频分量滤除,保留中高频段信号,传统滤波器带宽的选择主要依赖于专家经验,若滤波器选择不合理,则难以检测出微弱的异常信号分量。为此,本文引入快速峭度谱指标(式(11)),获得实时信号的冲击信号较强的频段,并以此频段作为带通滤波器的频带范围,实现滤波器参数的自适应选择。
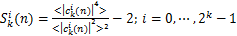 (11)
(11)
式中: 为信号通过第k个分解层的第i个滤波器的复包络。
为信号通过第k个分解层的第i个滤波器的复包络。
2) 提取滤波后的信号峰值,即选用固定时长的移动窗将原始信号截断为M个大小相同的数据序列,并在每个数据序列上计算峰值。在固定时长数据序列上保留峰值[18-20]。固定时长一旦选定,就直接确定了峰值能量的分辨率,一般取1/(2.56fmax),其中,fmax为待提取特征频率的最大频率。
3) 进一步对峰值提取信号在整个波形上进行平方整流,获得全波整流信号。
4) 对全波整流信号进行Hilbert变换,其目的是检测全波整流信号中的调制信号,这也是峰值能量法的关键组成部分。具体实现原理如下。
假设原始窄带信号 为
为
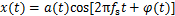 (12)
(12)
式中: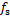 为载波频率;
为载波频率;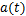 为
为 的包络(即调幅信号);
的包络(即调幅信号);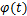 为
为 的相位调制信号。由于
的相位调制信号。由于 是窄带信号,因此,
是窄带信号,因此,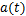 也是窄带信号,由此可设为
也是窄带信号,由此可设为
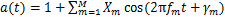 (13)
(13)
式中: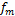 为调幅信号
为调幅信号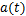 的频率分量;
的频率分量;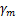 为
为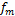 的各初始相位。
的各初始相位。
对 进行Hilbert变换,求其解析信号
进行Hilbert变换,求其解析信号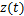 ,得到
,得到
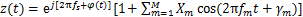 (14)
(14)
设
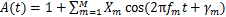 (15)
(15)
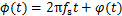 (16)
(16)
则解析信号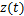 可重新表达为
可重新表达为
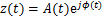 (17)
(17)
对比 表达式,得
表达式,得
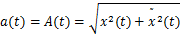 (18)
(18)
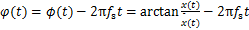 (19)
(19)
进一步采用相位解调求解频率解调 信号
信号
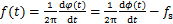 (20)
(20)
由此可知,采用Hilbert可以求解解析信号,获得原始信号中的幅值解调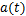 、相位解调
、相位解调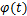 及解频率解调
及解频率解调 信号。
信号。
3 改进牵引电机轴承故障诊断方法
轴承缺陷时引起定转子气隙产生等周期的偏心冲击,转子气隙偏心又引起电机气隙长度变化,导致气隙磁通受到幅值调制作用,调制后磁通又在磁链上感应出相应的中高频谐波脉冲分量。为了提取磁链中特定的轴承故障特征分量,首先,通过磁链观测器模型实时计算电机磁链信号;然后,通过改进峰值能量谱,从磁链信号中提取微弱轴承故障谐波脉冲分量,实现轴承故障诊断,其原理如图3所示。
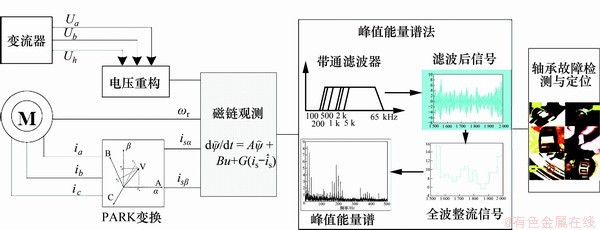
图3 基于改进磁链峰值能量法的轴承故障诊断流程图
Fig. 3 Flow chart of bearing fault diagnosis based on improved flux peak energy spectrum
3.1 电机磁链观测
以采集获得的电机电流、电机转速以及重构电压信号作为模型输入,采用磁链观测器模型,实时计算获得电机磁链观测值。采用异步电机全阶U-N模型对磁链进行观测。
首先,采用PARK变换对实测的电机电流信号进行转换,获得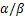 轴电流,其表达式为
轴电流,其表达式为
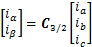 (21)
(21)
式中: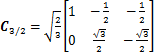 。
。
然后,将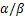 轴电流带入牵引电机观测器模型,结合异步电机闭环状态观测器表达式,如式(22),
轴电流带入牵引电机观测器模型,结合异步电机闭环状态观测器表达式,如式(22),
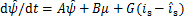 (22)
(22)
式中: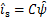 。
。
反馈矩阵取
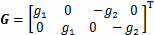 (23)
(23)
进一步将反馈矩阵式(23)代入式(22),可得[5]
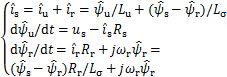 (24)
(24)
对应的全阶磁链观测器框图如4所示。
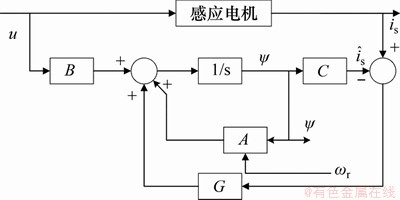
图4 全阶磁链观测器模型结构图
Fig. 4 Structure diagram of full-order flux linkage observer model
3.2 采用改进峰值能量谱检测轴承故障特征分量
1) 计算电机磁链观测信号的峭度谱指标,选取峭度谱指标最大的频段作为带通滤波器参数,并对磁链观测信号进行带通滤波,将低频高幅的电机电流基频及其等低频谐波分量滤除,保留有效的中高频谐波脉冲信号。
2) 选用固定时长的移动窗,提取每个移动窗内的峰值作为波形的1个数据点,获得全波信号。
3) 对全波信号进行平方处理,获得整流信号,并对平方整流后的信号进行Hilbert变换,获得包络解调信号。
4) 对包络解调信号进行FFT变换,获得磁链峰值能量法,提取出轴承故障的特征频率分量,实现牵引电机轴承内圈、外圈和滚动体故障诊断。
4 试验及现场验证结果分析
4.1 故障模拟试验验证
轴承故障模拟试验采用牵引电机传动试验台,电机选用某地铁用异步牵引电机,额定功率为192 kW,磁极对数为2,采用Y型接法。电机非传动端轴承型号为HC6215,传动端轴承型号为NU216。
电机电流、转速及中间电压等信号由牵引控制单元(driver control unit,DCU)进行实时采集。基于上述采集信号,DCU首先对电机三相电压进行重构获得三相重构电压,同时对三相电流进行PARK变换获得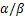 电流;然后,采用式(24)中的全阶电机磁链观测器模型计算获得电机磁链信号。
电流;然后,采用式(24)中的全阶电机磁链观测器模型计算获得电机磁链信号。
本次试验模拟2类轴承缺陷,分别是非传动端轴承滚动体和非传动端轴承内圈故障。滚动体故障轴承为现场搜集的电腐蚀故障轴承,内圈故障为人为在内圈滚道表面预置缺陷孔,轴承故障缺陷图片如图5所示。

图5 轴承故障缺陷图片
Fig. 5 Bearing fault picture
根据上述试验方案,对牵引电机滚动体缺陷工况下的实时磁链信号进行峰值能量谱分析。以电机转速为2 400 r/min为例,按照式(10)计算轴承滚动体故障特征频率,牵引电机非传动端轴承滚动体故障时磁链中的特征频率为227.98,164.57,291.39,131.39,324.57,392.56,519.37,552.56和620.53 Hz。
采用本文所提出的磁链峰值能量法算法对磁链信号进行变换,即首先对磁链原始波形进行带通滤波,然后对滤波后的信号进行峰值检波处理,每个阶段的波形图如图6所示。

图6 磁链信号滤波及峰值检波后的波形图
Fig. 6 Waveform diagram after flux signal filtering and peak detection
对峰值检波后的信号进行FFT变换获得磁链峰值能量法,如图7(a)所示。从图7(a)可知:磁链峰值能量法中出现明显的非传动端滚动体故障特征频率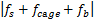 和
和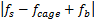 分量。
分量。
为了进一步说明本文所提方法的有效性,选取正常的相同型号轴承在同转速同负载工况下进行对比试验,同样采用本文所提方法计算磁链峰值能量E,如图7(b)所示。从图7(b)中没有出现明显的非传动端轴承故障特征频率分量,表明利用磁链信号分析轴承故障结果准确、可靠。
同样地,对牵引电机内圈缺陷工况下的实时磁链信号进行峰值能量谱分析。当转速为2 740 r/min时,根据式(10),计算出牵引电机非传动端轴承内圈故障在磁链中的特征频率为157.0,248.37,294.0,339.73,431.09,451.05,542.41,633.78,725.14和745.10 Hz。
通过分析磁链信号,获得的峰值能量谱如图7(c)所示。从图7(c)可见:在294.7 Hz和340.7 Hz处出现明显内圈故障特征分量,正常电机在磁链峰值能量法中没有出现该频率分量,说明这些特征分量是内圈缺陷导致转子动态偏心引起的,进一步验证了本文所提方法的有效性。
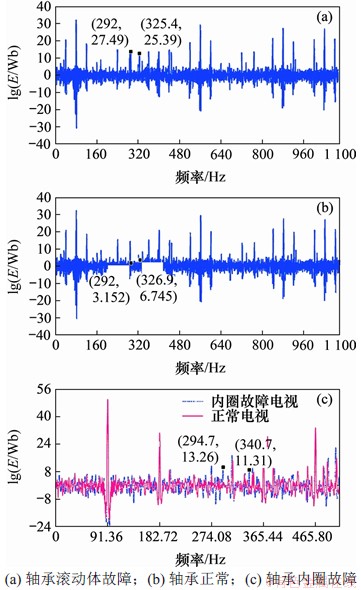
图7 不同故障工况下的磁链峰值能量法
Fig. 7 Peak energy spectrum of flux linkage under different fault conditions
4.2 现场应用验证
为进一步验证本方法的现场实际应用效果,先后在CR400AF滚动试验台和某地铁线城轨车辆上进行盲测验证。相对于轴承故障模拟试验台而言,CR400AF滚动试验台和地铁城轨车辆现场装车验证工况更接近实际工程应用场景,更能够验证算法的实际应用效果。
基于CR400AF滚动试验台,开展了5次盲测试验,根据本文所提方法分析盲测过程中所采集数据,在电机轴承不同故障模式下,分别求取磁链观测信号的峰值能量谱,如表1所示。然后,提取轴承内圈、外圈、滚动体和保持架故障特征频率处的幅值,以此作为轴承故障诊断的判据。
1) 若轴承某部位故障特征频率处出现明显偏高的幅值,则说明轴承该位置出现缺陷。
表1 CR400AF滚动试验台轴承故障盲测结果
Table 1 Blind test results of bearing faults on CR400AF rolling test bench

2) 若在峰值能量谱中发现滚动体故障特征频率处幅值明显偏大,则诊断为滚动体故障。
3) 若在峰值能量谱中发现内圈故障特征频率处幅值明显偏大,则诊断为内圈故障。
4) 若在峰值能量谱中同时发现滚动体和内圈故障特征频率处幅值明显偏大,则诊断为滚动体和内圈混合故障。最后,对比诊断结果与轴承真实故障情况,验证诊断结果的准确性。盲测试验结果表明:本文所提方法的5次诊断结果均与实际故障结果一致。
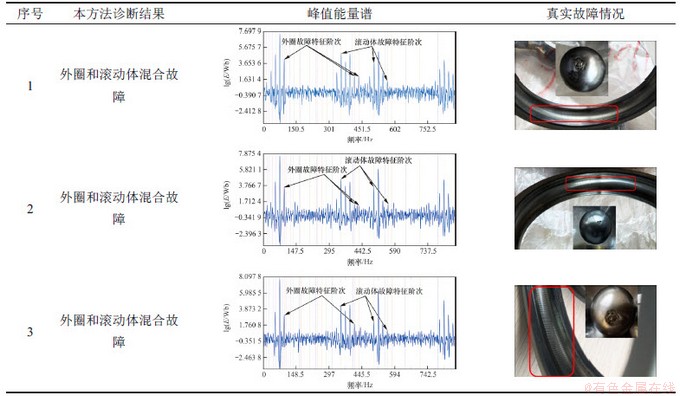
此外,2020-01-06—2020-04-10,在某地铁线上完成36列城轨车辆装车应用,涉及144辆动车,采用本文所提方法计算车载实时磁链数据的峰值能量谱,并自动检测轴承故障特征频率处的幅值明显程度,总计诊断出3辆动车牵引电机非传动端轴承外圈和滚动体混合故障特征,如表2所示,诊断结果为上述3辆动车牵引电机非传动端轴承出现外圈和滚动体混合故障。经轴承拆解,发现轴承外圈出现明显的“搓衣板”状故障缺陷,滚动体表面出现明显的局部剥落,3次诊断结果均与真实故障一致,进一步验证了本算法在实际工程应用中的诊断准确性和有效性。
表2 城轨车辆现场装车验证结果
Table 2 Results of on-site loading verification of urban rail vehicles
5 结论
针对轨道交通大功率牵引电机轴承故障诊断难题,本文提出了一种改进磁链峰值能量法的新型轴承故障诊断方法。首先分析了轴承故障机理,构建了轴承故障与磁链特征谱的映射关系,采用牵引电机全阶状态观测器进行磁链等信号的实时观测和计算,通过对磁链信号进行峰值平方整流和包络解调等处理,提取轴承故障磁链峰值能量法特征,解决了轴承故障微弱信号的提取难题,实现了对轴承外圈、内圈、滚动体等部位的精确诊断,并进行了相关试验验证和现场应用。试验及现场应用结果表明,本文所提的方法可有效实现轴承故障的精准诊断。
参考文献:
[1] ZHANG Xinpeng, HU Niaoqing, HU Lei, et al. A bearing fault diagnosis method based on sparse decomposition theory[J]. Journal of Central South University, 2016, 23(8): 1961-1969.
[2] 余发军, 周凤星. 基于可调Q因子小波变换和谱峭度的轴承早期故障诊断方法[J]. 中南大学学报(自然科学版), 2015, 46(11): 4122-4128.
YU Fajun, ZHOU Fengxing. Bearing early faults diagnosis based on tunable Q-factor wavelet transform and spectral kurtosis[J]. Journal of Central South University (Science and Technology), 2015, 46(11): 4122-4128.
[3] KOMPELLA K C D, RAO M V, RAO R S, et al. Bearing fault diagnosis in 3 phase induction machine using current spectral subtraction with different wavelet transform techniques[J]. Journal of Electrical Systems, 2017, 13(1): 143-159.
[4] HOANG D T, KANG H J. A motor current signal-based bearing fault diagnosis using deep learning and information fusion[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(6): 3325-3333.
[5] 张忠云, 吴建德, 马军, 等. 基于混沌分形理论的滚动轴承微小故障诊断[J]. 中南大学学报(自然科学版), 2016, 47(2): 640-646.
ZHANG Zhongyun, WU Jiande, MA Jun, et al. Slight fault diagnosis for rolling bearing based on chaos and fractal theory[J]. Journal of Central South University(Science and Technology), 2016, 47(2): 640-646.
[6] 杨江天, 赵明元. 改进双谱和经验模态分解在牵引电机轴承故障诊断中的应用[J]. 中国电机工程学报, 2012, 32(18): 116-122.
YANG Jangtian, ZHAO Mingyuan. Fault diagnosis of traction motor bearings using modified bispectrum and empirical mode decomposition[J]. Proceedings of the CSEE, 2012, 32(18): 116-122.
[7] 李雨琪. 基于电气法的电机轴承故障诊断技术[D]. 哈尔滨:哈尔滨工业大学电气工程系, 2018: 21-37.
LI Yuqi. Fault diagnosis technology of motor bearing based on electrical method[D]. Harbin: Harbin Institute of Technology. Department. of ELectrical Engineering, 2018: 21-37.
[8] 侯新国, 吴正国, 夏立, 等. 基于Park 矢量模信号小波分解的感应电机轴承故障诊断方法[J]. 中国电机工程学报, 2005, 25(14): 115-119.
HOU Xinguo, WU Zhengguo, XIA li, et al. Bearing fault diagnosis method of induction motor via wavelet decomposition of park's vector modulus signal[J]. Proceedings of the CSEE, 2005, 25(14): 115-119.
[9] 李青松. 基于定子电流分析的机车牵引电机轴承故障诊断[D]. 北京: 北京交通大学机械与电子控制工程学院, 2011: 23.
LI Qingsong. Locomotive Traction Motor Bearing Fault Detection via the Analysis of the Stator Current[D]. Beijing: Beijing Jiaotong University. School of Mechanical, Electronic and Control Engineering, 2011: 23.
[10] 薛征宇. 船舶感应电机轴承故障的检测方法研究[D]. 大连: 大连海事大学轮机工程学院, 2015: 27.
XUE Zhengyu. Research on the application methods of marine induction machine bearing fault detection[D]. Dalian: Dalian Maritime University. Marine Engineering College of Dalian Maritime University, 2015: 27.
[11] 万茜, 林永生, 肖沿海, 等. 基于MCSA的无人机电机轴承故障监测研究[C]// 2014(第五届)中国无人机大会论文集. 北京: 航空科学技术, 2014: 241-245.
WAN Qian, LIN Yongsheng, XIAO Yanhai, et al. Research on UAV motor bearing fault monitoring based on MCSA[C]// Proceedings of the Fifth China UAV Conference. Beijing: Aeronautical Science and Technology, 2014: 241-245.
[12] SCHOEN R R, HABETLER T G, KAMRAN F, et al. Motor bearing damage detection using stator current monitoring[J]. IEEE Transactions on Industry Applications, 1995, 31(6): 1274-1279.
[13] BLODT M, GRANJON P, RAISON B, et al. Models for bearing damage detection in induction motors using stator current monitoring[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1813-1822.
[14] MCFADDEN P D, SMITH J D. Model for the vibration produced by a single point defect in a rolling element bearing[J]. Journal of Sound and Vibration, 1984, 96(1): 69-82.
[15] WANG Y F, KOOTSOOKOS P J. Modeling of low shaft speed bearing faults for condition monitoring[J]. Mechanical Systems and Signal Processing, 1998, 12(3): 415-426.
[16] STACK J R, HABETLER T G, HARLEY R G. Bearing fault detection via autoregressive stator current modeling[J]. IEEE Transactions on Industry Applications, 2004, 40(3): 740-747.
[17] 李建勤, 胡玉荣, 胡继辉, 等. Peakvue技术在轴承故障诊断中的应用[J]. 中国设备工程, 2012(1): 17-19.
LI Jianqin, HU Yurong, HU Jihui, et al. Application of Peakvue technology in nearing fault diagnosis[J]. China Plant Engineering, 2012 (1): 17-19.
[18] 张铁新. 峰值能量技术原理及其应用[J]. 电机技术, 2010 (3):61-63.
ZHANG Tiexin. Application and principle of peak energy technology[J]. Electrical Machinery Techonology, 2010(3): 61-63.
[19] 柯燕亮, 王华庆, 唐刚, 等. 基于Teager峰值能量的低转速轴承故障特征提取方法[J]. 振动与冲击, 2017, 36(11): 124-128.
KE Yanliang, WANG Huaqing, TANG Gang, et al. Fault feature extraction of low speed roller bearing based on the Teager peak energy[J]. Journal of Vibration and Shock, 2017, 36(11): 124-128.
[20] 张军, 陆晨. PeakVue技术在滚动轴承故障诊断中的应用[J]. 设备管理与维修, 2018(4): 107-108.
ZHANG Jun, LU Chen. Application of PeakVue technology in fault diagnosis of rolling bearings[J]. Plant Maintenance Engineering, 2018(4): 107-108.
(编辑 秦明阳)
收稿日期: 2020 -05-02; 修回日期: 2020 -06 -23
基金项目(Foundation item):“十三五”国家重点研发计划项目(2016YFB1200401) (Project(51775037) supported by the"13th Five Year Plan" National Key Research & Development Plan of China)
通信作者:冯江华,博士,教授级高级工程师,从事大功率轨道交通交流传动控制研究;E-mail: fengjh@csrzic.com
引用格式: 冯江华. 基于改进磁链峰值能量法的牵引电机轴承故障诊断[J]. 中南大学学报(自然科学版), 2021, 52(4): 1380-1388.
Citation: FENG Jianghua. Fault diagnosis of traction motor bearing based on improved flux peak energy method[J]. Journal of Central South University(Science and Technology), 2021, 52(4): 1380-1388.