J. Cent. South Univ. (2020) 27: 2367-2381

DOI: https://doi.org/10.1007/s11771-020-4455-2

A generalized cover renewal strategy for multiple crack propagation in two-dimensional numerical manifold method

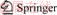
YU Chang-yi(ÓÚ³¤Ò»)^{1, 2, 3, 4}, ZHENG Fei(Ö£·É)⁵, GUO Bing-chuan(¹ù±þ´¨)², LIU Qin-ya(ÁõÇßÑÅ)⁶

1. China Communications Construction Company-Tianjin Port Engineering Institute, Co., Ltd.,Tianjin 300222, China;

2. China Communications Construction Company-First Harbor Engineering Company, Co., Ltd.,Tianjin 300461, China;

3. Key Laboratory of Geotechnical Engineering, Ministry of Communications, Tianjin 300222, China;

4. Key Laboratory of Geotechnical Engineering of Tianjin, Tianjin 300222, China;

5. Institute of Continuum Mechanics, Leibniz University Hannover, 30167 Hannover, Germany;

6. Department of Physics, University of Toronto, Canada

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: Partition of unity based numerical manifold method can solve continuous and discontinuous problems in a unified framework with a two-cover system, i.e., the mathematical cover and physical cover. However, renewal of the topology of the two-cover system poses a challenge for multiple crack propagation problems and there are few references. In this study, a robust and efficient strategy is proposed to update the cover system of the numerical manifold method in simulation of multiple crack propagation problems. The proposed algorithm updates the cover system with a bottom-up process: 1) identification of fractured manifold elements according to the previous and latest crack tip position; and 2) local topological update of the manifold elements, physical patches, block boundary loops, and non-persistent joint loops according to the scenario classification of the propagating crack. The proposed crack tracking strategy and classification of the renewal cases promote a robust and efficient cover renewal algorithm for multiple crack propagation analysis. Three crack propagation examples show that the proposed algorithm performs well in updating the cover system. This cover renewal methodology can be extended for numerical manifold method with polygonal mathematical covers.

Key words: numerical manifold method; multiple crack propagation; physical cover renewal; polygonal mathematical cover

Cite this article as: YU Chang-yi, ZHENG Fei, GUO Bing-chuan, LIU Qin-ya. A generalized cover renewal strategy for multiple crack propagation in two-dimensional numerical manifold method [J]. Journal of Central South University, 2020, 27(8): 2367-2381. DOI: https://doi.org/10.1007/s11771-020-4455-2.

1 Introduction

Crack propagation and discontinuous deformation exists in many problems in the fields of material science and geological engineering, such as failure of high strength ceramics, impact fracture of tempered glass, concrete cracking and failure of jointed rock mass [1, 2]. The analytical solutions to crack propagation problems with complex patterns are challenging considering the complex boundary conditions, various geometrical pattern, the dynamic effects, and the no-elastic behavior. Considering the feasibility, accuracy and efficiency, numerical approaches have been widely applied in analysis of fracture initiation,propagation and coalescence involving complex crack patterns. They are mainly classified into two categories: continuum-based method and discontinuum-based method [3, 4].

The commonly used continuum-based methods include the boundary element method (BEM) [5, 6], the mesh-free method (MMs) [7-10], the finite element method (FEM) [11, 12], the smoothed finite element method (SFEM) [13, 14], the embedded finite element method (EFEM) [15], the partition of unity method (PUM) [16], the generalized finite element method (GFEM) [17] and the extended finite element method (XFEM) [18-20]. Modeling crack propagation with FEM requires the mesh conformation regarding the crack geometry and remeshing is required during crack propagation. These lead to expensive computation cost and loss of accuracy as the data are mapped from the old mesh to the new mesh [20]. GFEM and XFEM use enrichment based on PUM [21] and remeshing is avoided. However, difficulties still exist for multiple cracking problems. MMs also avoid remeshing, but high-order integration schemes are required for rational shape functions. Furthermore, the treatment of boundary conditions is not straightforward since the shape functions are not interpolants in MMs. The discontinuum-based methods are also adopted in simulation of rock failure phenomenon, such as the commonly used discrete element method (DEM) [22, 23] and discontinuous deformation analysis (DDA) [24-27].

In the family of numerical methods, numerical manifold method (NMM) solves continuous and discontinuous deformation in a unified framework with its two-cover system, i.e., mathematical cover (MC) and physical cover (PC). The shape function is defined on MC while the displacement function is defined on PC. This two-cover system makes it suitable for analyzing fracturing problems [28-36]. To capture the crack propagation more accurately in the NMM framework, local mesh refinement and remeshing approaches have been applied [37]. The mass lumping scheme was also proposed for high order elements in NMM [38].

Regarding the topological operation of the NMM cover systems in fracture analysis, two fundamental issues should be addressed, i.e., the generation of initial cover system and the cover renewal during crack propagation process. For generation of the cover system, a generalized approach was proposed based on the concept of ¡°detached physical cover¡±, which considers both the distribution of discontinuous interfaces and inclusions [39]. For cover renewal in fracture analysis, several algorithms have been implemented [28-37, 40-42]. Most of them are limited to hexagonal/quadrangular MCs and simple crack patterns. They may not be suitable for polygonal MC shape or complex cases with intersection of multiple cracks. Moreover, the methodology and the procedure for updating the cover structure during multiple crack propagation cases is rarely given comprehensively. For NMM using polygonal shaped MCs, a generalized methodology according to crack tip positions can be applied for updating cover structures in crack propagation process. Based on this methodology of classifying the crack propagation scenarios, a robust cover renewal strategy is proposed in this paper for NMM simulation of crack propagation with complex patterns.

The paper is organized as follows. Basic concepts of NMM cover systems are reviewed first, followed by the detailed classification of crack propagation cases based on crack tip positions. Then the cover renewal procedure is given in detail. Three crack propagation examples are used to verify the feasibility and robustness of the proposed algorithm. A summary of the proposed approach is given in last section.

2 Generation and representation of cover system

For solution of continuous and discontinuous problem, two types of covers, MC and PC, are introduced in NMM. MC consists of finite simply connected domain that are named as mathematical patch (MP). In two-dimensional cases, hexagon and quadrangle are the commonly used MP shapes. The shape function is defined on each MP, which determines the precision of the solution. When the physical domain (PD) with all the discontinuities (e.g., cracks, joints, material interfaces) is introduced, the physical patches (PPs) can be created by cutting each MP with the boundaries of PD. If one MP is not cut by any physical boundaries, it naturally forms a PP. If one MP is segmented by some physical boundaries, it splits into several PPs. All PPs inside the PD will form the PC system. The displacement function is defined on each PP. During the generation of PPs, the overlapping parts of PPs are recognized as manifold element (ME). The numerical integration and assemblage of mass and stiffness matrix terms in global equilibrium equation is on the ME level.

Figure 1 illustrates the construction process of the cover system in NMM. In this example, a PD with a single edge crack is considered and the boundaries are marked by thick lines. 4 MPs (i.e., M₁, M₂, M₃ and M₄) are used to cover the PD. PPs can be obtained by cutting each MP with domain boundaries and internal discontinuities. In this example, physical patches P₁₁ and P₁₂ are formed from mathematical patch M₁; Physical patches P₂₁ and P₂₂ are formed from mathematical patch M₂; Physical patch P₃ is formed from mathematical patch M₃. Finally, the MEs are created by overlapping these PPs. In this example, manifold element E₁ is the intersection part of physical patches P₁₁, P₂₁ and P₃, while manifold element E₂ is the overlapping area of physical patches P₁₂, P₂₂ and P₃.

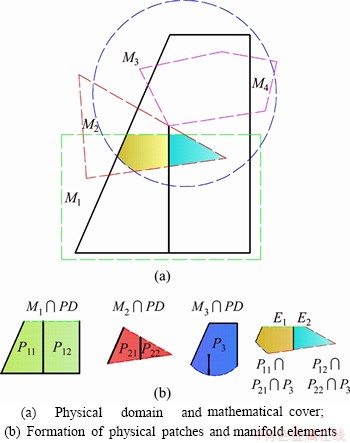
Figure 1 An illustration of two-cover system and manifold elements:

The commonly used MP shapes are hexagon [43-46] and quadrangle [47-50]. The topological data of model using the two-cover system are stored in a multi-level format. The node number and coordinate are the basis and they are stored on the bottom level. The numbers of MP, PP and ME are stored and their loops are linked with the node number. The numbers describing the loops are arranged counterclockwise as the convention way [51-53]. The relationship of ME and PP, and the linkage of PP and MP are also stored in either array or list format.

Using hexagon MP, Figure 2 illustrates the relationship of node, MP, PP and ME in topological representation of the cover system. As shown in Figure 2, A crack exists in a PD. The model consists of 9 nodes, 7 MPs, 8 PPs, 8 MEs, 1 block and 1 joint. ME 1 consists of three nodes, represented by loop 1-7-6-1. The three nodes of ME 1 are linked with three PPs, i.e., PP 1, PP 7 and PP 6₁. The loops of PP 1, PP 7 and PP 6₁ are 1-2-7-6-1, 1-2-3-4-5-8-9-8-6-1 and 6-1-7-9-8-6, respectively.

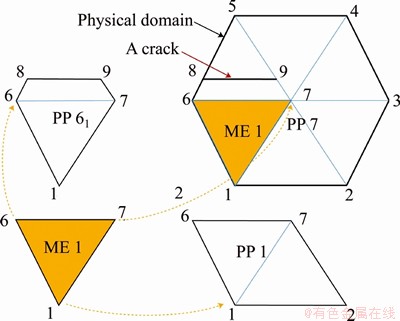
Figure 2 Topological relations of cover structure in NMM

3 Classification of crack propagation cases

During NMM simulation of crack propagation, the topological information of ME, PPs, domain loops, and joint loops should be updated stepwise. With different direction and length of the propagating crack, different PPs will be chosen for further renewal of the topological structure of the cover system. Figure 3 shows an example with four possible crack propagating directions. In case 1 and case 3 the crack extends to element node, while in case 2 and case 4 the crack extends to element edge. In case 1 and case 4, the PPs associated with mathematical patches M₃ and M₄ are cut. While in case 2 and case 3, only the PP associated with mathematical patch M₄ is split. In this section, all possible crack propagation cases are classified based on the current and previous positions of all crack tips. Basic assumptions and the case classification are shown in detail.

Figure 3 Examples of crack propagating directions

3.1 Assumption

For efficient topological renewal of the cover system encountering multiple cracks, the following crack propagation conditions are assumed: the propagating crack separates the targeting ME completely at one analysis step. Based on the assumption, cracks can propagate through multiple MEs at one step, but the new crack tip will reach either the edge or node of a ME. Meanwhile, crack can propagate to the boundary of a block and form new block loops. The cover updating algorithms can be proceeded according to the initial and propagated crack tip positions in the background cover system.

3.2 Case classification according to crack tip position

For two-dimensional finite-cover based NMM, the commonly used MP shapes are hexagon [43-46] and quadrangle [47-50]. These MP shapes are all belonging to polygons and the generated ME will be polygons. When a crack propagates thoroughly across a polygon, the intersection position of crack and polygon will be the node or edge of it.

According to the possible crack propagation trajectories and the crack tip positions in the background ME system, the cases can be summarized in Table 1. Figures 4-6 illustrate these cases in details. The old crack tips are marked by the small solid circle and the new crack tips are marked by empty circles. In Figures 4 and 5, the PDs are simply connected domains and their boundaries can be described by closed loops. The cracks in Figures 4 and 5 are called edge cracks. In Figure 6, the PD is multiple-connected and represented with two closed loops. The cracks in Figure 6 are called internal cracks. Particularly, when the new crack tip locates on the boundary of the PD, the number of closed loops maybe increases (Figure 5) or decreases (Figure 6). For example, new blocks are generated in case 8-1 while block number remains unchanged in case 8-2, as shown in Figures 5 and 6.

4 Cover renewal strategy

Once the crack propagation path is determined, the cracking MEs and associated cracking PPs would be updated. Particularly, the renewal of the joint loops and the block domains is possible depending on the geometrical relationship of the propagating crack, the joint loops, and the domain boundaries. The proposed approach to update the NMM cover structure during multiple crack propagation follows a bottom-top procedure. A flowchart of the cover renewal procedure is shown in Figure 7. The process starts with tracking the crack tips and its neighboring MEs. Once the propagation path is given, the targeting MEs and its associated PPs will be renewed according to the position of the crack tip. Note that a PP can be formed by gathering the MEs inside it. For cases that the crack tips reach block boundary, the block loop and joint loop will be checked and updated if necessary.

Table 1 Classification of crack propagation scenario according to crack tip location

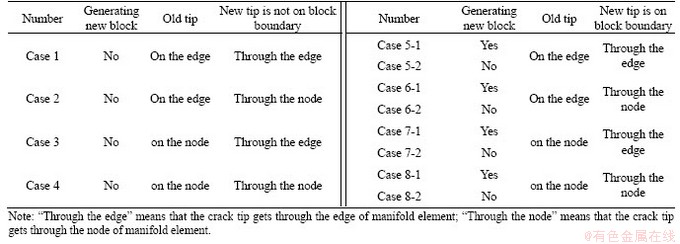
Figure 4 Crack propagation cases with new tip inside the block domain

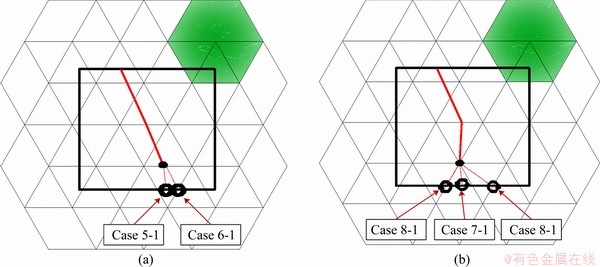
Figure 5 Crack propagation cases that new tip on block boundary and additional blocks are generated

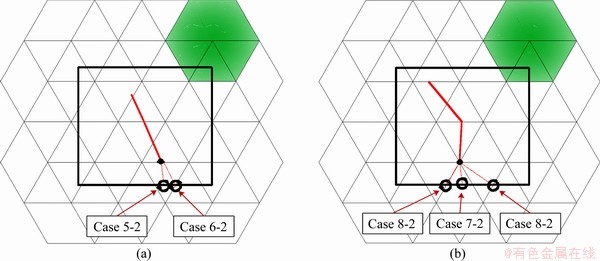
Figure 6 Crack propagation cases that new tip is on block boundary and no additional blocks are generated

Figure 7 Flowchart of proposed cover renewal algorithm

4.1 Detection of neighboring elements

The determination of fractured ME regarding the propagating crack is the requirement for the following renewal of cover structure. ¡°Neighboring element¡± is used here to locate the targeting ME which would possibly be passed by the propagating crack in following analysis step. When crack propagates, the new crack tip will be on the node or the edge from one of the neighboring elements. Once the crack propagation path is determined, one or more cracking neighboring elements can be obtained. The topological structure of these cracking MEs and associated PPs will be updated accordingly. Some details in updating PCs can be found in Refs. [39] and [42]. Figure 8 illustrates the establishment of neighboring element list for crack tips. The neighboring elements for crack tip 1 consist of manifold elements 1-7; The neighboring elements of the crack tip 2 are 6, 8, 9; The neighboring elements of the crack tip 3 are 10 and 11.

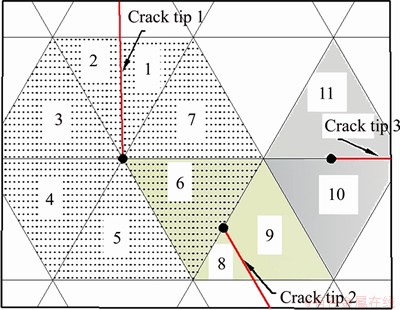
Figure 8 Illustrations of ¡°neighboring elements¡± of crack tip

4.2 Identification of propagation case

4.2.1 New tip in block

In this subsection, the case that new crack tip is still inside the block domain is discussed in details. The number of joint loops remains unchanged and only the targeting MEs and related PPs are necessary to be updated. Four possible crack propagation cases, i.e., from edge to edge (case 1), from edge to node (case 2), from node to edge (case 3), and from node to node (case 4), are shown in Figure 4 and the states of the associated PPs are shown in Figures 9(a)-(d), respectively.

In Figure 9, the carmine solid lines represent cracks; the filled dots represent the old crack tip; the empty circles represent the new crack tip. Figure 9(a) illustrates crack propagation case 1, from edge to edge. The crack propagates through manifold element A and stops at on the common side of manifold elements A and B. The renewal of node number of manifold elements A and B is necessary. Then, the physical patches PP(j) linked with the fractured manifold element A should be updated. The crack propagation cases 2, 3, and 4 are shown in Figures 9(b)-(d), respectively. Two new PPs are added in case 2 while one PP is added in other cases. Table 2 lists the updated data structure for all the possible cases during crack propagation. Note that during programming, the ME nodes and the joint loops are both identified with counterclockwise order. In order to save internal memory, fluctuating arrays are used to record the information of nodes, covers and the boundaries of the PD, and all elements share the unique point information. The recorded data are adjusted according to Table 2 during crack propagation.

4.2.2 New tip on block boundaries

In this subsection, the updating process of the cover system for cases that the new crack tip is on block boundaries are discussed. Still, there are four possible crack propagation cases, i.e., from edge to edge (case 5), from edge to node (case 6), from node to edge (case 7), and from node to node (case 8), are shown in Figure 5 and Figure 6. For each case, there will be two subcases according to the connectivity of joint loop and block domain. The associated PP states in these cases are shown in Figures 10 (a)-(d), respectively.

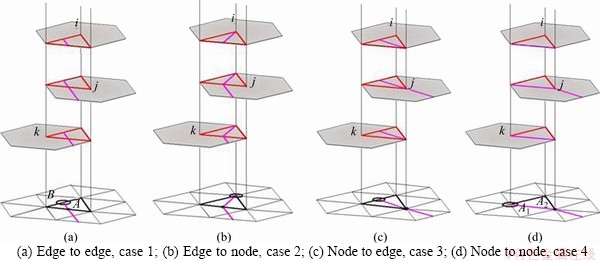
Figure 9 Sketches of updated PPs for cases 1, 2, 3 and 4 listed in Table 1:

Table 2 Updated data structure after crack propagation

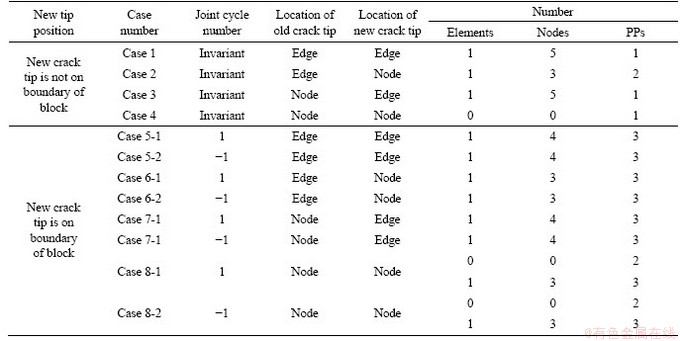
In cases 5-1, 6-1, 7-1 and 8-1, one endpoint is already on block boundary, and the other endpoint of the crack also propagates to block boundary. During these crack extension cases, the original block is split into two and the original joint loop increases to two loops, accordingly. By contrast, in cases 5-2, 6-2, 7-2 and case 8-2, both two end points of the crack are inside the block domain and one tip propagates to block boundary. In these cases, two separate joint loops combine into one loop, without generation of additional blocks.

In Figure 10, the pink solid lines represent crack and the thick black line is the boundary of the PD. The black dot is the old crack tip, and the empty circle is the new crack tip.

In Figure 10(a), manifold element A is divided into two elements during crack propagation and the node number increases from 6 to 10. The associated physical patches i, j and k are divided into two parts, and 3 new PPs are added accordingly. Figures 10(b)-(d) show other cases and the updates of topological data are listed in Table 2.

4.3 Renewal of physical patches

When a ME is split by a propagating crack, one or more PPs associated with it may also be split. Based on the configuration of the ME structure during crack propagation, the algorithm to updated associated PPs is introduced in details.

Figure 11 illustrates the PP updating process based on the hexagonal cover shape. Note that each ME has its own node ID system, and node ID belonging to different ME is linked to the same point coordinate. For example, in Figure 11(a), node 7 and node 16 refer to the same point while they belong to manifold elements 1₁26 and 246, respectively.

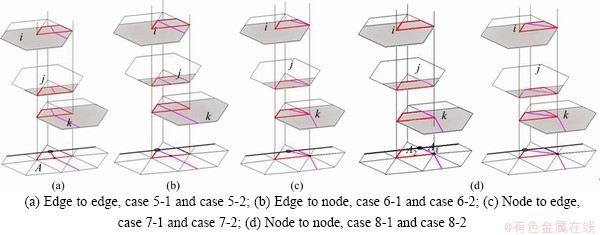
Figure 10 Sketches of updated PPs for cases 5, 6, 7 and 8 in Table 1:

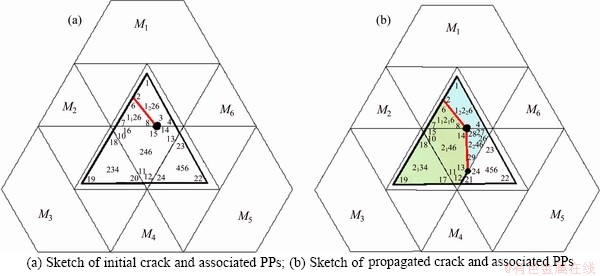
Figure 11 An illustration of PP updating process of case 1:

As shown in Figure 11(a), the neighboring elements of the crack tip can be located first, which is ME with closed loops of 6-7-8-6, 1-2-3-4-1 and 10-11-12-13-14-15-16-10. The three MEs are recorded as 1₁26, 1₂26 and 246, and the recorded number corresponds to associated PPs and MPs. Regarding to the propagated crack scenario as shown in Figure 11(b), the manifold element 10-11-12-13-14-15-16-10 is passed by the crack, and the topological structures of the associated physical patches 2, 4, and 6 need further updating. This is the case 1 in Figure 4(a) and Figure 9(a).

The original physical patch 2 is thoroughly passed by the crack and one PP should be added corresponding to mathematical patch 2. A simple way to create the two new PPs is as follows. First, all five MEs after the propagation can be established, which include 1-2-3-4-1, 6-7-8-6, 17-18-19-17, 10-11-12-13-14-15-10, and 26-27-28- 29-26, as shown in Figure 11(b). For this scenario, the MEs belonging to physical patch 2 can be classified into two groups based on their geometrical relationship with the crack. That is, the elements from the same side of the crack will gather into one group. Thus, manifold elements 6-7-8-6, 17-18-19-17 and 10-11-12-13-14-15-10 constitute the new physical patch 2₁ while manifold elements 1-2-3-4-1 and 26-27-28-29-26 constitute the new physical patch 2₂.

The updated PP 4 consists of the following MEs: 17-18-19-17, 10-11-12-13-14-15-10, 21-22- 23-24-21 and 26-27-28-29-26. These elements form a simply connected domain and thus the number of PP corresponding to mathematical patch 4 remains unchanged. Similarly, the updated PP 6 consists of MEs 10-11-12-13-14-15-10, 21-22-23-24-21, and 26-27-28-29-26. The PP number corresponding to MP 6 remains unchanged as the updated PP 6 forms a simply connected domain.

In addition to the case that a ME is split into two by the propagating crack, there are also cases that the cracking path is along the edge of MEs as shown in Figures 9(d) and 10(d). In this case, any ME sharing this cracking edge can be set as the fractured element. In the cases in Figures 9(d) and 10(d), the manifold element A₂ is chosen as the target, and the PPs associated with manifold element A₂ will be further checked and updated.

5 Representative numerical example

Three examples are simulated to verify the feasibility and robustness of the proposed approach in simulation of crack propagation problems. For examples in Sections 5.1 and 5.2, the Mohr- Coulomb strength criterion is introduced as the crack propagation criterion [30, 54]. The crack tip stress is expressed by the mean stress [55] of its neighboring area, i.e., the previously defined neighboring element. The NMM simulation results are compared with the published experimental results. The example in Section 5.3 is used to test the performance of proposed approach in multiple crack propagation scenario.

5.1 Semi-circular bend (SCB) test

The SCB experiment is an effective way to test the tensile strength of brittle materials, especially rocks [56-63]. It is commonly used to investigate the feasibility of the developed numerical methods [64-66]. AYATOLLAHI et al [62] tested the specimen involving central crack of different angles. XIE et al [66] applied XFEM to simulate the experiment [62] with the stress intensity factor criterion.

In this example, the Mohr Coulomb strength criterion [54] was introduced in NMM to simulate the experiment in Ref. [62]. The model configuration is as shown in Figure 12. The radius of the specimen is 50 mm. The flaw inclination angle ¦Â is set to 0¡ã, 10¡ã, 20¡ã, 30¡ã, 40¡ã, 43¡ã, 47¡ã and 50¡ã, respectively, and S/R=0.72. The parameters for the simulation are as follows: elastic modulus is 60 GPa; Poisson ratio is 0.2; tensile strength is 1 MPa; cohesion is 0.78 MPa; friction angle is 38¡ã.

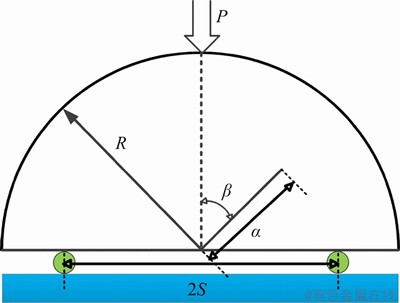
Figure 12 SCB model

Figure 13 shows the comparison of NMM simulation results and the SCB results. When ¦Â=0¡ã, the crack propagation is subjected to pure mode I, a crack emanates from the tip of the flaw and propagates exactly straight along the extended line of the flaw till the complete failure of the specimen. With the increasing flaw inclination angle ¦Â, the cracking type gradually transfers to mode II type. In this circumstance, the crack initiates at an angle to the original flaw line around the flaw tip, and then propagates along a curvilinear path that eventually aligns the center line of the specimen. It is found that simulated crack propagating trajectories for specimens with the length ratio of ¦Á/R=0.3 are in good agreement with previous experimental observations [62], as shown in Figure 13.

5.2 Double-edge notched (DEN) concrete beams with four-point shear loading

The double-edge notched (DEN) concrete beams test by four-point shear loading is commonly used to evaluate the strength of concrete materials. The earliest experimental tests for DEN concrete beams can trace back to the 1990s [67, 68]. Then, this model has been used to verify the feasibility of numerical approach in simulating crack propagation, such as the damage model [69], the FEM model [70], and the continuum strong discontinuity approach [71]. In this example, the experiments in Ref. [68] are investigated, and the model configuration is shown in Figure 14. The Mohr Coulomb strength criterion [54] is used to account for the crack propagation in the NMM model. The physical parameters in the simulation are as follows: elastic modulus is 30 GPa; Poisson ratio is 0.26; tensile strength is 3.9 MPa; cohesion is 3.2 MPa; friction angle is 40¡ã.

Figure 15 compares the experimental results [68] and the simulation results by proposed NMM approach. With anti-symmetry geometry and loading condition, the crack propagates and the fracturing pattern is also anti-symmetry. The cracking pattern by NMM simulation corresponds well with the experimental observation. Meanwhile, with the proposed NMM approach, remeshing is avoided, and a good result can be obtained even with rough meshes.

Figure 13 Comparison of experimental results and simulation result for semi-circular bend test:

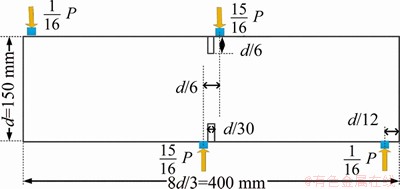
Figure 14 DEN model

5.3 Multiple crack propagation example

This example is used to test the performance of the proposed cover renewal algorithm in multiple crack propagation scenario. The simulation model,which consists of 62 PPs and 10 cracks, is illustrated as shown in Figure 16(a). There are 14 crack tips in total, and initially, they are located at the boundary of MEs. To test the proposed approach in simulating crack propagation, it is pre-assumed that all the cracks will propagate with the sequence from the smaller crack tip number to the larger crack tip number. Meanwhile, the crack propagating direction and propagating length are randomly determined by the user as follows. Crack tip 1 is assumed to propagate through two MEs, while other crack tips pass through just one element or stay still. The results after crack propagation are illustrated in Figure 16(b).

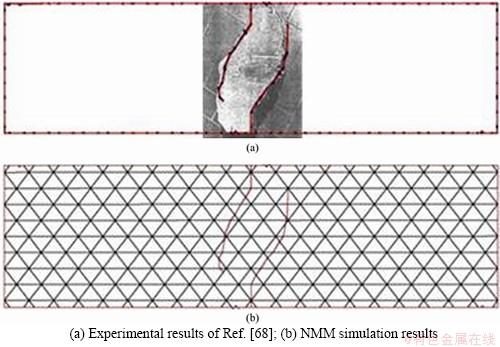
Figure 15 Comparison of experimental result and simulation result for double-edge notched concrete beams:

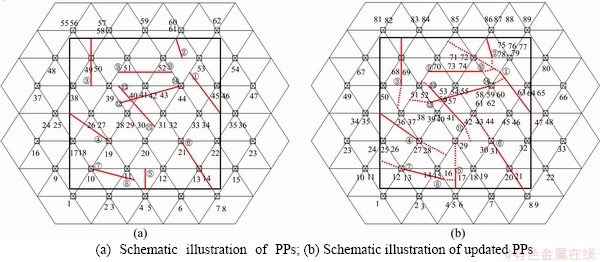
Figure 16 Schematic illustration of a complex crack propagation example:

It can be seen from Figure 16(b) that the number of PPs increases from 62 to 89 after crack propagation. Propagation of crack tips 1 to 6 initially belongs to side crack propagation case. Propagation of crack tip 1 includes edge-to-node situation (case 2) and node-to-edge situation (case 3). Propagation of crack tips 2 and 3 corresponds to the edge-to-edge situation (case 5-1 and case 1, respectively) and new block is generated during propagation of crack tip 2. Propagation of crack tips 4, 5 and 6 belongs to the node-to-edge type (case 3), edge-to-node type (case 2) and node-to-node type (case 4), respectively. By contrast, propagation of crack tips 7 to 14 initially belongs to internal crack case. Propagation of crack tip 7 belongs to case 7-2 while the later propagation of crack tip 8 belongs to case 5-1. A new block is generated after propagation of crack tip 8. For the case that propagation path of multiple crack tips is in the same ME (e.g., the propagation of crack tips 1, 2 and 10), the topological update of ME and the covers is correct, showing the robustness of the proposed approach in simulating complex crack propagation problems.

6 Conclusions

This paper proposes a robust cover updating algorithm for NMM simulation of multiple crack propagation problem. The cover renewal strategy assumes that the ME will be completely separated by a propagating crack passing it. This assumption also means that the crack tip will always stop on the boundary of a ME. For polygonal MPs, the crack will pass a ME through its node or edge. In view of this, the crack propagation scenarios can be classified into several cases based on the position of propagating crack tip, and a bottom-up cover updating scheme is proposed for NMM. The cover updating procedure includes the detection of neighboring MEs, identification of crack propagation cases and renewal of the PC system. The block loops and joint loops may be updated according to different cases.

In the proposed algorithm, only some neighboring elements near the old crack tips are necessary to locate the new crack tips and to detect the fractured elements. Meanwhile, only the PPs which are cut by the propagating cracks need to be updated. This bottom-up updating process is simple and efficient by tracking the propagating paths of all crack tips. The hexagon MP is used as an example to explain the implementation of the proposed algorithm. The simulation examples show the feasibility of the proposed algorithm in modeling multiple crack propagation problem. The idea and operation process of the new algorithm is fully applicable to polygonal shaped MPs within the NMM framework. The current work also has shortcomings. The work in this paper is limited to discussion of updating topological structure of the cover system during crack propagation, and lacks a thorough discussion of the crack propagation criteria and application in realistic complex crack propagation cases. Our future studies will be on solutions of above issues.

References

[1] ZHENG Fei, ZHUANG Xiao-ying, ZHENG Hong, JIAO Yu-yong, RABCZUK T. Kinetic analysis of polyhedral block system using an improved potential-based penalty function approach for explicit discontinuous deformation analysis [J]. Applied Mathematical Modelling, 2020, 82: 314-335. DOI: https://doi.org/10.1016/j.apm.2020.01.026.

[2] ZHENG Fei, LEUNG Andy, ZHU Jian-bo, JIAO Yu-yong. Modified predictor-corrector solution approach for efficient discontinuous deformation analysis of jointed rock masses [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(2): 599-624. DOI: https://doi.org/10.1002/nag.2881.

[3] SCHELDT T. Comparison of continuous and discontinuous modelling for computational rock mechanics [D]. Norway: Department of Geology and Mineral Rersources Engineering, Noraegion University of Science and Technology, 2003.

[4] JING L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering [J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(3): 283-353. DOI: https://doi. org/10.1016/S1365-1609(03)00013-3.

[5] WIPPLER K, KUNA M. Crack analyses in three- dimensional piezoelectric structures by the BEM [J]. Computational Materials Science, 2007, 39(1): 261-266. DOI: https://doi.org/10.1016/j.commatsci.2006.03.023.

[6] CORDEIRO S G F, LEONEL E D. Cohesive crack propagation modelling in wood structures using BEM and the tangent operator technique [J]. Engineering Analysis with Boundary Elements, 2016, 64: 111-121. DOI: https://doi.org/10.1016/j.enganabound.2015. 11.013.

[7] NGUYEN V P, RABCZUK T, BORDAS S, DUFLOT M. Meshless methods: A review and computer implementation aspects [J]. Mathematics and Computers in Simulation, 2008, 79(3): 763-813. DOI: https://doi.org/10.1016/j.matcom. 2008.01.003.

[8] LU Y Y, BELYTSCHKO T, GU L. A new implementation of the element free Galerkin method [J]. Computer Methods in Applied Mechanics and Engineering, 1994, 113(3): 397-414. DOI: https://doi.org/10.1016/0045-7825(94)90056-6.

[9] CAI Yong-chang, HAN Lin, TIAN Long-gang, ZHANG Lian-yang. Meshless method based on Shepard function and partition of unity for two-dimensional crack problems [J]. Engineering Analysis with Boundary Elements, 2016, 65: 126-135. DOI: https://doi.org/10.1016/j.enganabound. 2016.01.009.

[10] FRIES T P, MATTHIES H. Classification and overview of meshfree methods [R]. Technical Report, TU Brunswick, Germany Nr. 2003-03.

[11] BOUCHARD P O, BAY F, CHASTEL Y, TOVENA T. Crack propagation modelling using an advanced remeshing technique [J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(3): 723-742. DOI: https://doi.org/ 10.1016/S0045-7825(99)00324-2.

[12] BOUCHARD P O, BAY F, CHASTEL Y. Numerical modelling of crack propagation: Automatic remeshing and comparison of different criteria [J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(35, 36): 3887-3908. DOI: https://doi.org/10.1016/S0045-7825(03) 00391-8.

[13] LIU G R, DAI K Y, NGUYEN T T. A smoothed finite element method for mechanics problems [J]. Computational Mechanics, 2006, 39(6): 859-877. DOI: https://doi.org/10. 1007/s00466-006-0075-4.

[14] LIU G R, NGUYEN T T, DAI K Y, LAM K Y. Theoretical aspects of the smoothed finite element method (SFEM) [J]. Int J Numer Methods Eng, 2007, 71(8): 902-930. DOI: https://doi.org/10.1002/nme.1968.

[15] OLIVER J. Modelling strong discontinuities in solid mechanics via strain softening constitutive equations. Part 1: Fundamentals [J]. Int J Numer Methods Eng, 1996, 39(21): 3575-3600. DOI: https://doi.org/10.1002/(SICI)1097-0207 (19961115)39:21<3575::AID-NME65>3.0.CO;2-E.

[16] RABCZUK T, STEPHANE BORDAS, ZI G. On three-dimensional modelling of crack growth using partition of unity methods [J]. Computers & Structures, 2010, 88(23, 24): 1391-1411. DOI: https://doi.org/10.1016/j.compstruc. 2008.08.010.

[17] DUARTE C A, HAMZEH O N, LISZKA T J, TWORZYDLO W W. A generalized finite element method for the simulation of three-dimensional dynamic crack propagation [J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(15-17): 2227-2262. DOI: https://doi.org/10.1016/ j.compstruc.2008.08.010.

[18] SALIMZADEH S, KHALILI N. A three-phase XFEM model for hydraulic fracturing with cohesive crack propagation [J]. Computers and Geotechnics, 2015, 69: 82-92. DOI: https://doi.org/10.1016/j.compgeo.2015.05.001.

[19] XIE You-sheng, CAO Ping, LIU Jie, DONG Li-wei. Influence of crack surface friction on crack initiation and propagation: A numerical investigation based on extended finite element method [J]. Computers and Geotechnics, 2016, 74: 1-14. DOI: https://doi.org/10.1016/j.compgeo.2015. 12.013.

[20] BERGARA A, DORADO J I, MART¨ªN-MEIZOSO A, MARTINEZ-ESNADLA J M. Fatigue crack propagation in complex stress fields: experiments and numerical simulations using the extended finite element method (Xfem) [J]. International Journal of Fatigue, 2017. DOI: https:// doi.org/10.1016/j.ijfatigue. 2017.05.026.

[21] BABUSKA I, CALOZ G, OSBORN J E. Special finite element methods for a class of second order elliptic problems with rough coefficients [J]. SIAM Journal on Numerical Analysis, 1994, 31(4): 945-981. DOI: https://doi. org/10.1137/0731051.

[22] VESGA L, VALLEJO L, LOBO-GUERRERO S. DEM analysis of the crack propagation in brittle clays under uniaxial compression tests [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32: 1405-1415. DOI: https://doi.org/ 10.1002/nag.665.

[23] YANG Dong-min, SHENG Yong, YE Jian-qiao, TAN Yuan-qiang. Dynamic simulation of crack initiation and propagation in cross-ply laminates by DEM [J]. Composites Science and Technology, 2011, 71(11): 1410-1418. DOI: https://doi.org/ 10.1016/j.compscitech.2011.05.014.

[24] JIAO Yu-yong, ZHANG Xiu-li, ZHAO Jian. Two- dimensional DDA contact constitutive model for simulating rock fragmentation [J]. Journal of Engineering Mechanics, 2012, 138: 199-209. DOI: https://doi.org/10.1061/ (ASCE)EM.1943-7889.0000319.

[25] ZHANG Xiu-li, JIAO Yu-yong, ZHAO Jian. Simulation of failure process of jointed rock [J]. Journal of Central South University of Technology, 2008, 15: 888-894. DOI: https:// doi.org/10.1007/s11771-008-0162-0.

[26] SHI Gen-hua. Discontinuous deformation analysis: A new numerical model for the statics and dynamics of block systems [M]. Berkeley: University of California, 1988.

[27] NING You-jun, YANG Jun, AN Xin-mei, MA Guo-wei. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework [J]. Computers and Geotechnics, 2011, 38(1): 40-49. DOI: https://doi.org/10. 1016/j.compgeo.2010.09.003.

[28] TSAY R J, CHIOU Y J, CHUANG W L. Crack growth prediction by manifold method [J]. Journal of Engineering Mechanics, 1999, 125: 884. DOI: https://doi.org/ 10.1061/(ASCE)0733-9399(1999)125:8(884).

[29] ZHANG H H, LI L X, AN X M, MA G W. Numerical analysis of 2-D crack propagation problems using the numerical manifold method [J]. Engineering Analysis with Boundary Elements, 2010, 34(1): 41-50. DOI: https://doi.org/ 10.1016/j.enganabound.2009.07.006.

[30] WU Zhi-jun, WONG L N Y. Frictional crack initiation and propagation analysis using the numerical manifold method [J]. Computers and Geotechnics, 2012, 39: 38-53. DOI: https://doi.org/10.1016/j.compgeo.2011.08.011.

[31] HE Jun, LIU Quan-sheng, MA Guo-wei, ZENG Bin. An improved numerical manifold method incorporating hybrid crack element for crack propagation simulation [J]. International Journal of Fracture, 2016, 199(1): 21-38. DOI: 10.1007/ s10704-016-0084-z.

[32] KOUREPINIS D, PEARCE C, BICANIC N. Higher-order discontinuous modeling of fracturing in concrete using the numerical manifold method [J]. International Journal of Computational Methods, 2010, 7(1): 83-106. DOI: https:// doi.org/10.1142/S0219876210002076.

[33] ZHAO Gao-feng, MA Guo-wei, ZHANG Hui-hua, ZHAO Jian. A numerical manifold method for plane micropolar elasticity [J]. International Journal of Computational Methods, 2010, 7(1): 151-166. DOI: https://doi.org/10.1142/S021987621 0002106.

[34] LIU Feng, ZHENG Hong, DU Xiu-li. Hybrid analytical and MLS-based NMM for the determination of generalized stress intensity factors [J]. Mathematical Problems in Engineering, 2015, 2015: 1-9. DOI: https://doi.org/10.1155/ 2015/219657.

[35] ZHENG Hong, XU Dong-dong. New strategies for some issues of numerical manifold method in simulation of crack propagation [J]. Int J Numer Methods Eng, 2014, 97(13): 986-1010. DOI: https://doi.org/10.1002/nme.4620.

[36] ZHENG Hong, LIU Feng, DU Xiu-li. Complementarity problem arising from static growth of multiple cracks and MLS-based numerical manifold method [J]. Computer Methods in Applied Mechanics and Engineering, 2015, 295: 150-171. DOI: https://doi.org/10.1016/j.cma.2015.07.001.

[37] YANG Shi-kou, MA Guo-wei, REN Xu-hua, REN Feng. Cover refinement of numerical manifold method for crack propagation simulation [J]. Engineering Analysis with Boundary Elements, 2014, 43: 37-49. DOI: https://doi.org/ 10.1016/j.enganabound.2014.03.005.

[38] YANG Yong-tao, ZHENG Hong, SIVASELVAN M V. A rigorous and unified mass lumping scheme for higher-order elements [J]. Computer Methods in Applied Mechanics & Engineering, 2017, 319(1): 491-514. DOI: https://doi.org/ 10.1016/j.cma.2017.03.011.

[39] CAI Yong-chang, ZHUANG Xiao-ying, ZHU He-hua. A generalized and efficient method for finite cover generation in the numerical manifold method [J]. International Journal of Computational Methods, 2013, 10(5): 1350028. DOI: https://doi.org/10.1142/S021987621350028X.

[40] ZHANG H H, MA G W. Fracture modeling of isotropic functionally graded materials by the numerical manifold method [J]. Engineering Analysis with Boundary Elements, 2014, 38: 61-71. DOI: https://doi.org/10.1016/ j.enganabound.2013.10.006.

[41] ZHANG Hui-hua, YAN Jia-xiang. Investigation of the accuracy of the numerical manifold method on n-sided regular elements for crack problems [J]. Applied Mechanics and Materials, 2012, 157-158: 1093-1096. DOI: https://doi. org/10.4028/www.scientific.net/AMM.157-158.1093.

[42] MA G W, AN X M, ZHANG H H, LI L X. Modeling complex crack problems using the numerical manifold method [J]. International Journal of Fracture, 2009, 156(1): 21-35. DOI: https://doi.org/10.1007/s10704-009-9342-7.

[43] CHEN G Q, OHNISHI Y, ITO T. Development of high-order manifold method [J]. Int J Numer Methods Eng, 1998, 43(4): 685-712. DOI: https://doi.org/10.1002/(SICI)1097-0207 (19981030)43:4<685::AID-NME442>3.0.CO;2-7.

[44] LIN J S, KU C Y. Two-scale modeling of jointed rock masses [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(3): 426-436. DOI: https://doi.org/ 10.1016/j.ijrmms.2005.07.009.

[45] MIKI S, SASAKI T, KOYAMA T, NISHIYAMA S, OHNISHI Y O. Development of coupled discontinuous deformation analysis and numerical manifold method (NMM-DDA) and its application to dynamic problems [M]. Singapore: Research Publishing Services, 2010. DOI: https://doi.org/10.1142/S021987621 000209X.

[46] ZHANG G X, ZHAO Y, PENG X C. Simulation of toppling failure of rock slope by numerical manifold method [J]. International Journal of Computational Methods, 2010, 7(1): 167-189. DOI: https://doi.org/10.1142/S0219876210002118.

[47] CHEN G Q, JIANG Z S, WU Y Q. A new approach for numerical manifold method [J]. IEIT Journal of Adaptive & Dynamic Computing, 2012: 23-34. DOI: https://doi.org/10. 5813/www.ieit-web.org/IJADC/2012.2.5.

[48] ZHANG H H, CHEN Y L, LI L X, et al. Accuracy comparison of rectangular and triangular mathematical elements in the numerical manifold method [C]// Analysis of Discontinuous of Deformation New Developments and Applications: Vol.1. Singapore: Research Publishing Services. 2010: 297-303. DOI: https://doi.org/10.3850/ 9789810844554-0130.

[49] ZHANG Z, ZHANG X. Direct simulation of low-re flow around a square cylinder by numerical manifold method for navier-stokes equations [J]. Journal of Applied Mathematics, 2012: 465972. DOI: https://doi.org/10.1155/2012/465972.

[50] ZHANG Z R, ZHANG X W, LU W G. Numerical method based on compatible manifold element for thin plate bending [J]. Chin J Mech Eng, 2010, 23(1): 100-109. DOI: https://doi.org/10.3901/CJME.2010.01.100.

[51] WU Zhi-jun, WONG L N Y. Modeling cracking behavior of rock mass containing inclusions using the enriched numerical manifold method [J]. Engineering Geology, 2013, 162: 1-13. DOI: https://doi.org/10.1016/j.enggeo.2013.05. 001.

[52] WU Zhi-jun, WONG L N Y. Elastic¨Cplastic cracking analysis for brittle¨Cductile rocks using manifold method [J]. International Journal of Fracture, 2013, 180(1): 71-91. DOI: https://doi.org/10.1007/s10704-012-9802-3.

[53] WU Zhi-jun, WONG L N Y, FAN Li-feng. Dynamic study on fracture problems in viscoelastic sedimentary rocks using the numerical manifold method [J]. Rock Mechanics and Rock Engineering, 2013, 46(6): 1415-1427. DOI: https://doi.org/ 10.1007/s00603-012-0349-4.

[54] NING Y J, AN X M, MA G W. Footwall slope stability analysis with the numerical manifold method [J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(6): 964-975. DOI: https://doi.org/ 10.1016/j.ijrmms.2011.06.011.

[55] AN Xin-mei, NING You-jun, MA Guo-wei, HE Lei. Modeling progressive failures in rock slopes with non-persistent joints using the numerical manifold method [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(7): 679-701. DOI: https://doi.org/ 10.1002/nag.2226.

[56] LIM I L, JOHNSTON I W, CHOI S K. Stress intensity factors for semi-circular specimens under three-point bending [J]. Engineering Fracture Mechanics, 1993, 44(3): 363-382. DOI: https://doi.org/10.1016/0013-7944(93)900 30-v.

[57] LIM I L, JOHNSTON I W, CHOI S K, BOLAND J N. Fracture testing of a soft rock with semi-circular specimens under three-point bending. Part 1¡ªmode I [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(3): 185-197. DOI: https://doi.org/10.1016/0148- 9062(94)90463-4.

[58] LIM I L, JOHNSTON I W, CHOI S K, BOLAND J N. Fracture testing of a soft rock with semi-circular specimens under three-point bending. Part 2¡ªmixed-mode [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(3): 199-212. DOI: https://doi.org/ 10.1016/0148-9062(94)90464-2.

[59] ADAMSON R M, DEMPSEY J P, MULMULE S V. Fracture analysis of semi-circular and semi-circular-bend geometries [J]. International Journal of Fracture, 1996, 77(3): 213-222. DOI: https://doi.org/10.1007/bf00018778.

[60] AYATOLLAHI M R, ALIHA M R M. On determination of mode II fracture toughness using semi-circular bend specimen [J]. International Journal of Solids and Structures, 2006, 43(17): 5217-5227. DOI: https://doi.org/10.1016/ j.ijsolstr.2005.07.049.

[61] CHEN R, XIA K, DAI F, LU F, LUO S N. Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing [J]. Engineering Fracture Mechanics, 2009, 76(9): 1268-1276. DOI: https://doi.org/10.1016/j.engfracmech.2009.02.001.

[62] AYATOLLAHI M R, ALIHA M R M, HASSANI M M. Mixed mode brittle fracture in PMMA¡ªAn experimental study using SCB specimens [J]. Materials Science and Engineering A, 2006, 417(1, 2): 348-356. DOI: https://doi. org/10.1016/j.msea.2005.11.002.

[63] ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 423-439. DOI: https://doi.org/10.1016/j.ijrmms.2013.01.005.

[64] ALIHA M R M, AYATOLLAHI M R, SMITH D J, PAVIER M J. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading [J]. Engineering Fracture Mechanics, 2010, 77(11): 2200-2212. DOI: https://doi.org/10.1016/j.engfracmech.2010.03.009.

[65] XU Y, DAI F, XU N W, ZHAO T. Numerical investigation of dynamic rock fracture toughness determination using a semi-circular bend specimen in split hopkinson pressure bar testing [J]. Rock Mechanics and Rock Engineering, 2015, 49(3): 731-745. DOI: https://doi.org/10.1007/s00603-015- 0787-x.

[66] XIE Y, CAO P, JIN J, WANG M. Mixed mode fracture analysis of semi-circular bend (SCB) specimen: A numerical study based on extended finite element method [J]. Computers and Geotechnics, 2017, 82: 157-172. DOI: https://doi.org/10.1016/j.compgeo.2016.10.012.

[67] BOCCA P, CARPINTERI A, VALENTE S. Size effects in the mixed mode crack propagation: Softening and snap-back analysis [J]. Engineering Fracture Mechanics, 1990, 35(1): 159-170. DOI: https://doi.org/10.1016/0013-7944(90)901 93-K.

[68] SCHLANGEN E. Experimental and numerical analyses of fracture processes in concrete [D]. The Netherlands: Department of Civil Engineering, Delft University of Technology, 1993.

[69] GEERS M, BORST R, PEERLINGS R H J. Damage and crack modeling in single-edge and double-edge notched concrete beams [J]. Engineering Fracture Mechanics, 2000, 65: 247-261. DOI: https://doi.org/10.1016/S0013-7944(99) 00118-6.

[70] ZHU Wan-cheng, TANG Chun-an. Numerical simulation on shear fracture process of concrete using mesoscopic mechanical model [J]. Construction and Building Materials, 2002, 16: 453-463. DOI: https://doi.org/10.1016/s0950- 0618(02)00096-x.

[71] OLIVER J, HUESPE A, SAMANIEGO E, CHAVES E W. Continuum approach to the numerical simulation of material failure in concrete [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28: 609-632. DOI: https://doi.org/10.1002/nag.365.

(Edited by YANG Hua)

ÖÐÎĵ¼¶Á

¶þάÊýÖµÁ÷Ðη¨ÔÚÄ£Äâ¶àÁÑÎÆÀ©Õ¹ÖеÄÒ»ÖÖͨÓø²¸Ç¸üвßÂÔ

ÕªÒª£ºÊýÖµÁ÷Ðη¨ÊÇ»ùÓÚÙ¤ÁɽðÌåϵϵĵ¥Î»·Ö½â·¨£¬¿ÉÒÔͳһ´¦ÀíÁ¬ÐøºÍ·ÇÁ¬ÐøÎÊÌâ¡£ÊýÖµÁ÷Ð稵ÄË«¸²¸ÇϵͳµÄÉú³ÉÓë¸üÐÂÔÚ·ÖÎö¶àÁÑÎÆÀ©Õ¹Ê±ÓкܴóµÄÌôÕ½£¬ÇÒºÜÉÙÓÐÎÄÏ׶Դ˽øÐÐÏêϸÌÖÂÛ¡£ÔÚ±¾Ñо¿ÖУ¬Õë¶ÔÊýÖµÁ÷Ðη¨ÔÚ¶àÁÑÎÆÀ©Õ¹¸²¸Ç¸üеÄÄѵ㣬Ìá³öÁËÒ»¸ö³°ôÐԽϺõIJßÂÔ¡£¸ÃË㷨ͨ¹ý×Ôµ×ÏòÉϵĹý³Ì¸üи²¸Çϵͳ£º1)¸ù¾ÝÁÑÎƼâ¶ËµÄоÉλÖÃʶ±ðÐèÒª¸üеÄÁ÷Ðε¥Ôª£»2)¸ù¾ÝÁ÷Ðε¥Ôª±»ÇиîµÄÇé¿ö£¬¸ù¾Ý·ÖÀàÒÀ´Î¸üнڵãϵͳ¡¢Á÷Ðε¥ÔªÏµÍ³¡¢ÎïÀí¸²¸ÇϵͳºÍ¿éÌåϵͳ¡£Ìá³öµÄÁÑÎƸú×Ù²ßÂԺ͸üа¸ÀýµÄ·ÖÀ࣬Ϊ¶àÖØÁÑÎÆÀ©Õ¹·ÖÎöÌṩÁËÒ»ÖÖÎȽ¡ÓÐЧµÄ¸²¸Ç¸üÐÂËã·¨¡£Èý¸öÁÑÎÆÀ©Õ¹ÊµÀý±íÃ÷£¬¸ÃËã·¨¿É׼ȷ¶Ô¶àÁÑÎÆÀ©Õ¹Ê±µÄ¸²¸Çϵͳ½øÐÐÍØÆ˸üС£ÕâÖÖ¸²¸Ç¸üз½·¨¿ÉÒÔÍƹ㵽¾ßÓжà±ßÐÎÊýѧ¸²¸ÇµÄÊýÖµÁ÷Ðη½·¨¡£

¹Ø¼ü´Ê£ºÊýÖµÁ÷Ð稣»¶àÁÑÎÆÀ©Õ¹£»ÎïÀí¸²¸Ç¸üУ»¶à±ßÐÎÊýѧ¸²¸Ç

Foundation item: Project(51321065, 51479191, 11672360) supported by the National Natural Science Foundation of China

Received date: 2019-09-20; Accepted date: 2020-06-20

Corresponding author: ZHENG Fei, PhD, Postdoc Researcher; Tel: +49-511762-17535; E-mail: feizhengprchina@hotmail.com; ORCID: https://orcid.org/0000-0003-2321-9112