风化壳淋积型稀土矿一维柱浸过程的模拟
来源期刊:中国有色金属学报(英文版)2019年第3期
论文作者:龙平 王观石 田君 胡世丽 罗嗣海
文章页码:625 - 633
关键词:风化壳淋积型稀土矿;柱浸;离子交换;溶质运移
Key words:weathered crust elution-deposited rare earth ore; column leaching; ion exchange; solute transport
摘 要:通过杯浸试验确定浸矿的离子交换模型为Kerr模型,得到Kerr模型的选择系数为12.59×10-10 L2/g2;采用对流-弥散方程描述柱浸过程铵根离子和稀土离子的运移规律,通过Kerr模型确定对流-弥散方程中的源汇项,运用顺序非迭代法解具有强非线性的对流-弥散方程,模拟稀土离子在土柱中的运移过程。与室内一维柱浸试验稀土离子的穿透曲线进行比较,两者的相关系数达到0.8724,说明本方法可以较为准确地模拟风化壳淋积型稀土矿一维柱浸过程。分析硫酸铵溶液浓度对稀土浸取率的影响,结果发现,最优硫酸铵溶液浓度( )与稀土品位(η)满足线性关系。
Abstract: The ion exchange model of the leaching process was determined via batch leaching experiments using the Kerr model, with the selectivity coefficient experimentally determined to be 12.59×10-10 L2/g2. Solute transport laws of ammonium ions (NH4+) and rare earth ions (RE3+) in column leaching were described by the convection-dispersion equation (CDE). The source and sink in the CDE were determined by the Kerr model. The CDE with strong nonlinearity was solved using the sequential non-iterative method. Compared with the breakthrough curve of RE3+, the correlation coefficient between the simulated and experimental curves reached 0.8724. Therefore, this method can simulate the one-dimensional column leaching of weathered crust elution-deposited rare earth ore. Moreover, the effects of different concentrations of ammonium sulfate ((NH4)2SO4) solution on the leaching rate of rare earth were analyzed. The optimal concentration of the (NH4)2SO4 solution had a linear relationship with the rare earth grade.
Trans. Nonferrous Met. Soc. China 29(2019) 625-633
Ping LONG1,2, Guan-shi WANG3, Jun TIAN1,4, Shi-li HU3, Si-hai LUO3
1. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. Cooperative Innovation Center of Efficient Development and Application for Ionic Rare Earth Resources, Jiangxi University of Science and Technology, Ganzhou 341000, China;
3. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
4. Institute of Applied Chemistry, Jiangxi Academy of Sciences, Nanchang 330029, China
Received 20 March 2018; accepted 11 October 2018
Abstract: The ion exchange model of the leaching process was determined via batch leaching experiments using the Kerr model, with the selectivity coefficient experimentally determined to be 12.59×10-10 L2/g2. Solute transport laws of ammonium ions (NH4+) and rare earth ions (RE3+) in column leaching were described by the convection-dispersion equation (CDE). The source and sink in the CDE were determined by the Kerr model. The CDE with strong nonlinearity was solved using the sequential non-iterative method. Compared with the breakthrough curve of RE3+, the correlation coefficient between the simulated and experimental curves reached 0.8724. Therefore, this method can simulate the one-dimensional column leaching of weathered crust elution-deposited rare earth ore. Moreover, the effects of different concentrations of ammonium sulfate ((NH4)2SO4) solution on the leaching rate of rare earth were analyzed. The optimal concentration of the (NH4)2SO4 solution had a linear relationship with the rare earth grade.
Key words: weathered crust elution-deposited rare earth ore; column leaching; ion exchange; solute transport
1 Introduction
The basic process of the exploitation of weathered crust elution-deposited rare earth (RE) ore based on the in-situ leaching technique is as follows. First, ammonium sulfate ((NH4)2SO4) solution is injected into the ore body via the injection well network. Second, ammonium ions (NH4+) in the (NH4)2SO4 solution are used to exchange RE ions (assuming the average valence of RE ions is +3, RE3+), which are adsorbed onto clay particles and the RE3+ enters the solution. RE3+ moves with the solution until it flows out of the ore body and enters into the solution collection system [1-5]. The exchange of the solid-phase RE3+ (i.e., the RE3+ is adsorbed by clay particles) by the liquid-phase NH4+ (i.e., the NH4+ in solution) is a solid-liquid reversible ion exchange reaction [6,7]. The (NH4)2SO4 concentration determines the exchange efficiency. Presently, the appropriate (NH4)2SO4 concentration is usually estimated by experience. Owing to the complexity of geological conditions, different mines have different RE grades, permeabilities, and impurities of the ion content. Therefore, the concentration of the (NH4)2SO4 solution determined by experience is often beyond the reasonable range. Too high a concentration of (NH4)2SO4 will lead to excessive ammonia nitrogen in the surrounding water bodies, and thus environmental pollution. However, low concentrations will result in an insufficient leaching rate of RE and cause resource waste. Establishing a mathematical model for the leaching process provides theoretical reference for the reasonable determination of a suitable (NH4)2SO4 concentration.
Leaching of RE ore primarily includes two processes: one is the RE3+ leaching (ion exchange process) and the other is the RE3+ transport (transport process). TIAN et al [8-10] analyzed the ion exchange process of RE ore using the shrinking core model and found that the ion exchange process was controlled by inner diffusion. The leaching kinetics when using ammonium salt solution [11] and magnesium sulfate solution [12] as the leaching agents have also been studied, and researchers [13-15] have attempted to analyze the column leaching process with the leaching kinetic model. Studies [16-19] of ion exchange and the transport of RE3+ are mainly based on laboratory experiments; however, solute transport of RE3+ has a distinct scale effect and laboratory experimental results are often inapplicable to practical engineering. WU et al [20-22] elaborated on the ion exchange and transport mechanism in the heap leaching process, which provided direction for the theoretical analysis of leaching. QIU et al [23,24] simulated the leaching process of weathered elution-deposited RE ore using the lattice Boltzmann theory.
In the preset study, an ion exchange model of RE ore was obtained using batch leaching experiments. NH4+ and RE3+ in the column leaching process were described by the convection-dispersion equation (CDE) and the source and sink of the CDE were determined by the ion exchange model. The feasibility of the proposed method was verified with a laboratory experiment. The proposed method was used to determine the optimal concentration of (NH4)2SO4.
2 Experimental
2.1 Batch leaching experiments
Samples were collected from RE ore in Xinfeng County, Jiangxi Province, China, and were screened with a high-frequency sieve shaker having a sifter diameter of 2 mm. Screened mineral samples were baked for 10 h in 110 °C oven to eliminate water in the mineral samples. (NH4)2SO4 solutions with different mass concentrations (2, 3, 4, 5, 6, 7 and 8 g/L) were prepared in volumetric flasks. Next, another seven iodine flasks were used to mix 20 g of mineral sample and 100 mL of (NH4)2SO4 solution with different mass concentrations (2-8 g/L). These seven iodine flasks were first placed in a constant temperature (30 °C) water tank and vibrated for 2 h, and then remained static for 0.5 h. Leachate and mineral samples were separated by medium-speed filter paper and concentrations of RE3+ in the leachate were tested using the EDTA titration method. Three parallel experiments were performed.
2.2 Column leaching experiments
Column leaching experiments were performed with the mineral samples. The RE grade of the mineral samples was 0.101%. Length, radius, and porosity of the soil column were set at 0.80 m, 5.2 cm and 1.15%, respectively. The initial water content in the soil column was set to be 17.1%. The porous stone, which was wet with deionized water, was placed into a PVC tube with an inner diameter of 10.4 cm and a length of 1 m. One 1 cm-thick coarse sand filtering layer was paved and samples were filled in eight layers. Another 1 cm-thick coarse sand filtering layer was paved at the top of the soil column. A piece of overflow pipe was installed 5 cm above the coarse sand filtering layer and deionized water was added to the water tank. Water inflow in the PVC tube was controlled by a faucet. To control the height of ponding to be 5 cm, the velocity of the water inflow was fast enough to spill from the overflow pipe. After stabilization of the water flow in the soil column, the ponding at the top of the soil column was quickly extracted. Water in the water tank was changed into 20 g/L (NH4)2SO4 solution. The ponding of the soil column quickly increased to 5 cm. The flow rate of the faucet was adjusted to maintain a constant head.
After replacement of the deionized water with the (NH4)2SO4 solution, the mass of the leachate in the conical flask was weighed every 4 h (assuming the leachate density was 1 g/cm3). Next, 10 mL leachate was added to oxalic acid. If no white precipitation was observed, this indicated that there was no RE3+ in the leachate. When RE3+ was detected in the testing solution, leachate was collected every 2 h thereafter. The concentration of RE3+ was tested using the EDTA titration method. The concentration of NH4+ in the leachate was tested using the formaldehyde method. The concentration of sulfate ions ( ) in the leachate was tested using the permanent white precipitation method. After the concentrations of RE3+, NH4+ and
) in the leachate was tested using the permanent white precipitation method. After the concentrations of RE3+, NH4+ and  were stabilized close to zero, the experiment was stopped. The breakthrough curves of RE3+, NH4+ and
were stabilized close to zero, the experiment was stopped. The breakthrough curves of RE3+, NH4+ and  were constructed.
were constructed.
3 Results and discussion
3.1 Ion exchange model
It is a solid-liquid ion exchange process for the liquid-phase NH4+ to exchange the solid-phase RE3+. The Kerr model, Vanselow model, and Gapon model are common ion exchange models used to describe this solid-liquid ion exchange process. The expressions of the selectivity coefficients of these three models are as follows [25]:
 (1)
(1)
 (2)
(2)
 (3)
(3)
where KK, KV and KG are the selectivity coefficients of the Kerr model, Vanselow model, and Gapon model, respectively.  and
and  refer to the concentrations of the liquid-phase NH4+ and liquid-phase RE3+, respectively, g/L.
refer to the concentrations of the liquid-phase NH4+ and liquid-phase RE3+, respectively, g/L.  and
and  are the concentrations of the solid-phase NH4+ and solid-phase RE3+, respectively, g/g. γN and γR are the activity coefficients of the liquid-phase NH4+ and liquid-phase RE3+, respectively, which are calculated from the Davies empirical model (Eq. (4)).
are the concentrations of the solid-phase NH4+ and solid-phase RE3+, respectively, g/g. γN and γR are the activity coefficients of the liquid-phase NH4+ and liquid-phase RE3+, respectively, which are calculated from the Davies empirical model (Eq. (4)).  and
and  are the molar fractions of the solid-phase NH4+ and solid-phase RE3+, which are calculated using Eqs. (5) and (6), respectively. MN and MR are the relative molecular masses of NH4+ and RE3+, respectively, g/mol.
are the molar fractions of the solid-phase NH4+ and solid-phase RE3+, which are calculated using Eqs. (5) and (6), respectively. MN and MR are the relative molecular masses of NH4+ and RE3+, respectively, g/mol.
 (4)
(4)
 (5)
(5)
 (6)
(6)
where A is the parameter related to the temperature, A=0.513 (mol/L)-1/2 in 30 °C aqueous solution; m is the valence state of the corresponding ions; μ is the ion strength.
Initially, there was no RE3+ in the liquid-phase and no NH4+ was adsorbed during the solid-phase. Ions in the solid-phase and liquid-phase met the following three equality relations before and after the ion exchange process: (1) the amount of substance of solid-phase NH4+ was 3 times that of the liquid-phase RE3+; (2) in the system composed of liquid-phase and solid-phase, NH4+ and RE3+ met the law of mass conservation; (3) after ion exchange equilibrium, the sum of the amount of substance of the liquid-phase NH4+ and solid-phase NH4+ was equal to the amount of substance of the liquid-phase NH4+ before leaching. These processes are expressed by Eqs. (7)-(9):
 (7)
(7)
 (8)
(8)
 (9)
(9)
where ms is the mass of the mineral sample, VL is the volume of the solution,  is the concentration of NH4+ in the leaching agent, and
is the concentration of NH4+ in the leaching agent, and  is the initial concentration of the solid-phase RE3+.
is the initial concentration of the solid-phase RE3+.
Substituting Eqs. (7)-(9) into Eqs. (1)-(3), the selectivity coefficients of the three models are the uniform functions of the concentration of liquid-phase RE3+. Given VL/ms,  ,
,  and
and  , the selectivity coefficients of the three models were calculated using the experimental data (Fig. 1).
, the selectivity coefficients of the three models were calculated using the experimental data (Fig. 1).

Fig. 1 Relationship between concentration of (NH4)2SO4 and that of liquid-phase RE3+

Fig. 2 Relationship between concentration of (NH4)2SO4 and selectivity coefficients for Kerr model, Vanselow model and Gapon model
The concentration of the liquid-phase RE3+ was obtained by leaching with different concentrations of (NH4)2SO4, as shown in Fig. 1. Combined with the experimental data from Fig. 1, the selectivity coefficients of the three models under different (NH4)2SO4 concentrations are shown in Fig. 2, where the selectivity coefficient of the Kerr model is amplified by 1010 times and the selectivity coefficient of the Vanselow model is amplified by 101 times. The selectivity coefficient is often assumed to be constant. The mean selectivity coefficient under various (NH4)2SO4 concentrations was calculated using data from Fig. 2. The selectivity coefficients of the Kerr model, Vanselow model, and Gapon model were calculated to be 12.59×10-10 L2/g2, 0.89 L2/mol2, and 3.43 (mol/L)-2/3, respectively.
The calculated selectivity coefficients of the three models were then substituted into Eqs. (1)-(9). The concentration of the liquid-phase RE3+ was used as the basic unknown variable. The concentration of the liquid-phase RE3+ under different (NH4)2SO4 concentrations in the three models was calculated. The calculated results and experimental data are shown in Fig. 3. Relative errors and the mean of relative errors (Eq. (10)) between the calculated results for each model and experimental data are listed in Table 1. It was found that the relative errors of the Kerr model and Vanselow model are close and basically within 10.00% (although when the concentration of (NH4)2SO4 was 2.0 g/L, the relative error of the Kerr model was 10.32%, which is slightly higher than 10.00%). The mean relative error of the Kerr model was slightly smaller than that of the Vanselow model. The calculation of the Gapon model deviated significantly from the experimental data under low concentrations of (NH4)2SO4. The mean relative error of the Gapon model was more than twice that of the Kerr model and the Vanselow model, indicating that the Kerr model and the Vanselow model are better than the Gapon model. Compared to the Vanselow model and the Gapon model, the Kerr model had a lower mean relative error and a simpler mathematical expression. Therefore, the ion exchange process of leaching was described using the Kerr model. The selectivity coefficient of the Kerr model for the chosen mineral samples was 12.59×10-10 L2/g2. The value of the selectivity coefficient for the Kerr model reflects the adsorption capacity of clays in terms of NH4+ and RE3+. The mineral samples have a very small selectivity coefficient, indicating a significantly higher adsorption capacity of RE3+ by clay particles than that of NH4+. If exchanging RE3+ adsorbed on the clay surface by NH4+, then the concentration of NH4+ would be far higher than the concentration of RE3+.

Fig. 3 Relationship between concentration of liquid-phase RE3+ and that of (NH4)2SO4 for Kerr model, Vanselow model and Gapon model
Table 1 Relative error (%) and mean relative error (%) of concentration of liquid-phase RE3+ between experimental data and calculated data for three models

This is consistent with the research conclusions of LI [26] and CHI and TIAN [6].
 (10)
(10)
where N is the experimental data number and  is the experimental data for the liquid-phase RE3+ concentration.
is the experimental data for the liquid-phase RE3+ concentration.
3.2 Hydrodynamic dispersion coefficient and mean flow velocity in pores
Mineral samples have low  adsorption capacity in solution [27]. In the present study,
adsorption capacity in solution [27]. In the present study,  was assumed to be a non-reactive solute and the transport of
was assumed to be a non-reactive solute and the transport of  was described by the CDE. The approximation solution of the breakthrough curve of
was described by the CDE. The approximation solution of the breakthrough curve of  was expressed as per SAUTY [28]:
was expressed as per SAUTY [28]:
 (11)
(11)
where erfc is the complementary error function,  is the concentration of liquid-phase
is the concentration of liquid-phase  ,
,  is the concentration of
is the concentration of  in the leaching agent, L is length of the soil column, u is the average flow velocity in pores, D is the hydrodynamic dispersion coefficient, and t is time.
in the leaching agent, L is length of the soil column, u is the average flow velocity in pores, D is the hydrodynamic dispersion coefficient, and t is time.
In the case of a non-reactive solution and convection domination, the time corresponding to the breakthrough curve 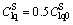 is the time for solute transport from the top to the bottom of the soil column, at the average flow velocity in pores [28], which is denoted as t0.5. The average flow velocity in pores can be expressed as u=L/t0.5. After infiltration in the column leaching experiment became stable, the water content in the soil column was 0.449. Breakthrough curves of RE3+, NH4+, and
is the time for solute transport from the top to the bottom of the soil column, at the average flow velocity in pores [28], which is denoted as t0.5. The average flow velocity in pores can be expressed as u=L/t0.5. After infiltration in the column leaching experiment became stable, the water content in the soil column was 0.449. Breakthrough curves of RE3+, NH4+, and  are shown in Fig. 4, with t0.5=5.26 d and the average flow velocity in the pores calculated as 0.152 m/d. Based on the least squares method, the breakthrough curve of
are shown in Fig. 4, with t0.5=5.26 d and the average flow velocity in the pores calculated as 0.152 m/d. Based on the least squares method, the breakthrough curve of  was fitted using Eq. (11) and the hydrodynamic dispersion coefficient of the soil column was calculated as 8.88×10-5 m2/d.
was fitted using Eq. (11) and the hydrodynamic dispersion coefficient of the soil column was calculated as 8.88×10-5 m2/d.

Fig. 4 Breakthrough curves of RE3+, NH4+ and 
3.3 Breakthrough curves of NH4+ and RE3+
The soil column was assumed to be a homogeneous medium. Considering the ion exchange process, the solute transport equations of NH4+ and RE3+ were expressed as
 (12)
(12)
 (13)
(13)
where ρb is the density of the soil column and θ is the volume water content.
To solve Eq. (12) and Eq. (13), the boundary condition was required. The concentration of the liquid-phase NH4+ at the top of the soil column was equal to the concentration of NH4+ in the leaching agent, and it remained constant over time. Initially, the concentrations of the liquid-phase NH4+ and liquid-phase RE3+ in the soil column were zero. The concentration gradients of the liquid-phase NH4+ and liquid-phase RE3+ at the bottom of the soil column were zero. Therefore, the boundary conditions for the liquid-phase NH4+ and the liquid-phase RE3+ were
 (14)
(14)
 (15)
(15)
The ion exchange process during leaching was described by the Kerr model. The relationship between the concentration of NH4+ and RE3+ is expressed in Eq. (1). According to conservation of the adsorption sites on the mineral samples, there is
 (16)
(16)
Initially, the concentration of the solid-phase RE3+ at any position in the soil column was equal to the concentration of the solid-phase RE3+ before leaching, and the concentration of the solid-phase NH4+ at any position in the soil column was zero. At the bottom of the soil column, the concentration gradients of the solid- phase NH4+ and solid-phase RE3+ were zero. Therefore, the boundary conditions for the solid-phase NH4+ and solid-phase RE3+ were
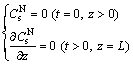 (17)
(17)
 (18)
(18)
The equation set consisting of Eqs. (1), (12), (13) and (16) represents the solute transport equation for NH4+ and RE3+ in the one-dimensional column leaching process. The solute transport equation of NH4+ and RE3+ showed strong non-linearity. Under the boundary conditions of Eqs. (14), (15), (17) and (18), directly solving the solute transport equation requires abundant computer memory [29]. To avoid occupying a large amount of computer memory during computation, the transport process and ion exchange process were considered independently using the sequential non-iterative method [30,31]. First,  and
and  were calculated by the transport process. Second, the ion exchange process was considered to correct
were calculated by the transport process. Second, the ion exchange process was considered to correct  ,
,  ,
,  and
and  . The detailed calculation process is shown below.
. The detailed calculation process is shown below.
The solute transport equation expressed by NH4+ and RE3+, with sole consideration to the transport process (source and sink terms in Eqs. (12) and (13) were eliminated), was written in a differential form:

 (19)
(19)

 (20)
(20)
where k is the time nodes (k=0, 1, 2, …, nk-1, nk, is the total number of time nodes); i is the positional nodes (i=1, 2, 3, …, ni-1, ni, is the total number of positional nodes); △t is the time step length; △z is the positional step length.
The boundary conditions in Eqs. (14) and (15) were also expressed in differential form:
 (21)
(21)
 (22)
(22)
When k=0 and i=1, the values of  ,
,  and
and  were obtained by Eq. (21) and are
were obtained by Eq. (21) and are  , 0 and 0, respectively. Substituting
, 0 and 0, respectively. Substituting  ,
,  and
and  into Eq. (19), the value of
into Eq. (19), the value of  was calculated. The process of transport and ion exchange affected the liquid-phase concentrations of NH4+ and RE3+. For discrimination, the concentrations of the liquid-phase NH4+ and the liquid-phase RE3+, with sole consideration to the transport process, were recorded as
was calculated. The process of transport and ion exchange affected the liquid-phase concentrations of NH4+ and RE3+. For discrimination, the concentrations of the liquid-phase NH4+ and the liquid-phase RE3+, with sole consideration to the transport process, were recorded as  and
and  . The concentrations of the liquid-phase NH4+ and liquid-phase RE3+ with consideration to both the transport process and ion exchange process were recorded as
. The concentrations of the liquid-phase NH4+ and liquid-phase RE3+ with consideration to both the transport process and ion exchange process were recorded as 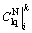 and
and  . It can be seen from Eq. (22) that
. It can be seen from Eq. (22) that  ,
,  and
and 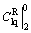 were all zero. Substituting them into Eq. (20), the value of
were all zero. Substituting them into Eq. (20), the value of  was then calculated.
was then calculated.
The ion exchange process occurred at the same time. The concentration of NH4+ and RE3+ in the liquid-phase and solid-phase, at time level k+1 and position level i, was described by the relationship in Eq. (1), which was rewritten into the discrete form as follows:
 (23)
(23)
The difference between the mole number of the solid-phase NH4+ after ion exchange and the mole number before ion exchange was 3 times the difference between the mole number of the liquid-phase RE3+ after ion exchange and the mole number before ion exchange, expressed as
 (24)
(24)
where  is the liquid-phase RE3+ concentration at time level k+1 and position level i before ion exchange; msi is the mass of mineral sample in the unit cell i; msi=ρsπr2△z/(1+e), ρs is the density of soil particles, e is the porosity and r is radius of the soil column; VLi is the volume of solution in the unit cell i and VLi=πr2△zθ.
is the liquid-phase RE3+ concentration at time level k+1 and position level i before ion exchange; msi is the mass of mineral sample in the unit cell i; msi=ρsπr2△z/(1+e), ρs is the density of soil particles, e is the porosity and r is radius of the soil column; VLi is the volume of solution in the unit cell i and VLi=πr2△zθ.
NH4+ and RE3+ met the law of mass conservation before and after ion exchange at position level i. Therefore,
 (25)
(25)
 (26)
(26)
where  is the concentration of the liquid-phase NH4+ at time level k+1 and position level i before ion exchange.
is the concentration of the liquid-phase NH4+ at time level k+1 and position level i before ion exchange.
The boundary conditions of the solid-phase NH4+ and RE3+ in Eqs. (17) and (18) were written in a differential form as follows:
 (27)
(27)
 (28)
(28)
When k=0 and i=1, the values of  and
and  were obtained from Eqs. (19)-(22). Given KK,
were obtained from Eqs. (19)-(22). Given KK,  ,
,  ,
,  and
and  , substituting Eqs. (24)–(26) into Eq. (23), the nonlinear equation of
, substituting Eqs. (24)–(26) into Eq. (23), the nonlinear equation of  was obtained. This nonlinear equation was solved by the fzero function in MATLAB. The calculated
was obtained. This nonlinear equation was solved by the fzero function in MATLAB. The calculated  was used in Eqs. (24)–(26) to calculate
was used in Eqs. (24)–(26) to calculate  ,
,  and
and  . When k=0 and i=2, the boundary conditions were combined with the previous two steps. Similarly,
. When k=0 and i=2, the boundary conditions were combined with the previous two steps. Similarly,  ,
,  ,
,  and
and  were calculated. Then, the values of
were calculated. Then, the values of  ,
,  ,
,  and
and  were calculated in the same manner.
were calculated in the same manner.
The breakthrough curve of the one-dimensional column leaching experiment in Section 2.2 was simulated using the above method. Simulation parameters were identical to those in the column leaching experiment. △t and △z were determined to be 1×10-3 d and 1×10-3 m, respectively. The breakthrough curve of RE3+ calculated using the proposed method is shown in Fig. 5. The correlation coefficient between the simulated and experimental curves reached 0.8724, indicating that the proposed method could accurately simulate the breakthrough curves of RE3+ in the one-dimensional column leaching experiment.

Fig. 5 Simulated and experimental breakthrough curves of RE3+
3.4 Optimization of ammonium sulfate solution
The breakthrough curve of RE3+ under different concentrations of (NH4)2SO4 was acquired using the proposed method, with the rest of the parameters remaining the same as those in the column leaching experiment. The breakthrough curves of RE3+ under 5.0, 10.0 and 20.0 g/L concentrations of (NH4)2SO4 are shown in Fig. 6. With the decrease in (NH4)2SO4 concentrations, the peak concentration of the breakthrough curves of RE3+ decreased, and the tailing phenomenon of the breakthrough curves became more obvious, combined with a longer leaching period and lower leaching rate of RE. The curves depicting the relationship between the concentration of (NH4)2SO4 and the leaching rate of RE are shown in Fig. 7. For a given RE grade (η), the leaching rate of RE was positively related to the concentration of (NH4)2SO4. There exists a concentration where the leaching rate of RE is constant after the concentration of (NH4)2SO4 exceeds this concentration. This concentration is called the optimal concentration of (NH4)2SO4 ( ). The curve for the relationship between
). The curve for the relationship between  and η is shown in Fig. 8, which showed a linear relationship. Based on linear fitting,
and η is shown in Fig. 8, which showed a linear relationship. Based on linear fitting,  =10.19η. Based on the relation equation between
=10.19η. Based on the relation equation between  and η, the consumption of (NH4)2SO4 decreased under the premise of satisfying the leaching rate of RE. This offers theoretical reference for choosing the suitable concentration of (NH4)2SO4 during RE exploitation using the in-situ leaching technique.
and η, the consumption of (NH4)2SO4 decreased under the premise of satisfying the leaching rate of RE. This offers theoretical reference for choosing the suitable concentration of (NH4)2SO4 during RE exploitation using the in-situ leaching technique.

Fig. 6 Breakthrough curves of RE3+ under different concentrations of (NH4)2SO4

Fig. 7 Variation curves of leaching rate of RE with different concentrations of (NH4)2SO4

Fig. 8 Relationship between optimal concentration of (NH4)2SO4 ( ) and RE grade (η)
) and RE grade (η)
4 Conclusions
(1) Compared with the Vanselow model and Gapon model, the Kerr model was more suitable for describing the ion exchange process of RE leaching. The selectivity coefficient of the Kerr model was experimentally determined to be 12.59×10-10 L2/g2.
(2) Using the Kerr model as the source-sink term, the transport process of RE3+ in a one-dimensional soil column was simulated with the CDE model. The correlation coefficient between the simulated and experimental breakthrough curves of RE3+ reached 0.8724, which indicates that the proposed method provides a good simulation of one-dimensional column leaching of weathered crust elution-deposited RE ore.
(3) The concentration of (NH4)2SO4 was optimized by the proposed model. It was shown that the optimal concentration of (NH4)2SO4 ( ) varied linearly with the RE grade (η). Under the conditions in the present study, the equation can be expressed as
) varied linearly with the RE grade (η). Under the conditions in the present study, the equation can be expressed as  =10.19η.
=10.19η.
References
[1] TANG Xun-zhong, LI Mao-nan. In-situ leach mining of ion-absorbed rare-earth mineral [J]. Mining Research and Development, 1996, 17(2): 1-4. (in Chinese)
[2] TANG Xun-zhong, LI Mao-nan, YANG Dian. The research of indoor simulation experiments of the ion-absorbed rare earth mineral in-situ leach mining [J]. Journal of Central South University of Technology, 1999, 30(2): 133-136. (in Chinese)
[3] QIU Ting-sheng, FANG Xi-hui, WU Hong-qiang, ZENG Qing-hua, ZHU Dong-mei. Leaching behaviors of iron and aluminum elements of ion-absorbed-rare-earth ore with a new impurity depressant [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(9): 2986-2990.
[4] JING Qing-xiu, CHAI Li-yuan, HUANG Xxiao-dong, TANG Chong-jian, GUO Huan, WANG Wei. Behavior of ammonium adsorption by clay mineral halloysite [J]. Transactions of Nonferrous Metals Society of China, 2017, 27(7): 1627-1635.
[5] YIN Sheng-hua, QI yan, XIE Fang-fang, CHEN Xun, WANG Lei-ming. Permeability characteristic of weathered crust elution- deposited rare earth ores under different pore structures [J]. The Chinese Journal of Nonferrous Metals, 2018, 28(5): 1043-1049. (in Chinese)
[6] CHI Ru-an, TIAN Jun. Weathered crust elution-deposited rare earth ores [M]. New York: Nova Science Publishers, 2008.
[7] TIAN Jun. Kinetics and mass transfer in leaching rare earth from the weathered crust elution-deposited rare earth ore [D]. Changsha: Central South University, 2010. (in Chinese)
[8] TIAN Jun, LU Sheng-liang, YIN Jing-qun. Kinetic study on leaching a south china rare earth ore [J]. Engineering Chemistry and Metallurgy, 1995, 16(3): 354-357. (in Chinese)
[9] TIAN Jun, CHI Ru-an, YIN Jing-qun. Leaching process of rare earths from weathered crust elution-deposited rare earth ore [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(5): 892-896.
[10] TIAN Jun, YIN Jing-qun, CHI Ru-an, RAO Guo-hua, JIANG Min-tao, OUYANG Ke-xian. Kinetics on leaching rare earth from the weathered crust elution-deposited rare earth ores with ammonium sulfate solution [J]. Hydrometallurgy, 2010, 101(3-4): 166-170.
[11] LI Ying-ting, TU An-bin, ZHANG Yue-fei, ZHANG Mei, CHI Ru-an. Kinetics of leaching rare earth from a weathered crust elution- deposited rare earth ore in South China with mixed ammonium salt [J]. Industrial Minerals and Processing, 2009(2): 19-24. (in Chinese)
[12] XIAO Yan-fei, CHEN Ying-ying, FENG Zong-yu, HUANG Xiao-wei, HUANG Li, LONG Zhi-qi, CUI Da-li. Leaching characteristics of ion-adsorption type rare earths ore with magnesium sulfate [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(11): 3784-3790.
[13] HE Zheng-yan, ZHANG Zhen-yue, YU Jun-xia, ZHOU Fang, XU Yuan-lai, XU Zhi-gao, CHEN Zhe, CHI Ru-an. Kinetics of column leaching of rare earth and aluminum from weathered crust elution-deposited rare earth ore with ammonium salt solutions [J]. Hydrometallurgy, 2016, 163: 33-39.
[14] RAN Xiu-chuan, REN Zi-jie, GAO Hui-min, ZHENG Ren-ji, JIN Jun-xun. Kinetics of rare earth and aluminum leaching from Kaolin [J]. Minerals, 2017, 7(9): 152-164.
[15] SUN Yuan-yuan, XU Qiu-hua, LI Yong-xiu. Leaching kinetics of ion adsorption rare earths using low concentration of ammonium sulfate solution [J]. Chinese Rare Earths, 2017, 38(4): 61-67. (in Chinese)
[16] WANG Rui-xiang, XIE Bo-yi, YU Pan, ZHANG Zhao-xue, MAO Ji-yong, XIONG Jia-chun. Selection of leaching agent and optimization of column leaching process of ion-absorbed rare earth deposits [J]. Chinese Journal of Rare Metals, 2015, 39(11): 1060-1064. (in Chinese)
[17] HE Zheng-yan, ZHANG Zhen-yue, YU Jun-xia, XU Zhi-gao, XU Yuan-lai, ZHOU Fang, CHI Ru-an. Column leaching process of rare earth and aluminum from weathered crust elution-deposited rare earth ore with ammonium salts [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(11): 3024-3033.
[18] HE Zheng-yan, ZHANG Zhen-yue, YU Jun-xia, XU Zhi-gao, CHI Ru-an. Process optimization of rare earth and aluminum leaching from weathered crust elution-deposited rare earth ore with compound ammonium salts [J]. Journal of Rare Earths, 2016, 34(4): 413-419.
[19] HE Zheng-yan, ZHANG Zhen-yue, CHI Ru-an, XU Zhi-gao, YU Jun-xia, WU Ming, BAI Ru-yu. Leaching hydrodynamics of weathered elution-deposited rare earth ore with ammonium salts solution [J]. Journal of Rare Earths, 2017, 35(8): 824-830.
[20] YIN Sheng-hua, WU Ai-xiang, HU Kai-jian, WANG Hong-jiang. Solute transportation mechanism of heap leaching and its influencing factors [J]. Journal of Central South University (Science and Technology), 2011, 42(4): 1092-1098. (in Chinese)
[21] WU Ai-xiang, YIN Sheng-hua, WANG Hong-jiang, SU Yong-ding. Solute transport mechanism and model of dump leaching [J]. Journal of Central South University (Science and Technology), 2006, 37(2): 385-389. (in Chinese)
[22] WU Ai-xiang, LIU Jin-zhi, YIN Sheng-hua, XI Yong. The mathematical model of the solute transportation in the heap leaching and the analytic solutions [J]. Mining and Metallurgical Engineering, 2005, 25(5): 7-10. (in Chinese)
[23] QIU Ting-sheng, ZHU Dong-mei, WU Cheng-you, WANG L M. Lattice Boltzmann model for simulation on leaching process of weathered elution-deposited rare earth ore [J]. Journal of Rare Earths, 2017, 37(10): 1014-1021.
[24] WU Cheng-you, QIU Ting-sheng, WANG Li-ming. Numerical study on solute transport in leaching process of rare earth by lattice Boltzmann method [J]. The Chinese Journal of Process Engineering, 2014, 14(5): 730-736. (in Chinese)
[25] EVANGELOU V P, PHILLIPS R E. Comparison between the Gapon and Vanselow exchange selectivity coefficients [J]. Soil Science Society of America Journal, 1988, 52(2): 379-382.
[26] LI Yong-xiu. Ion adsorption rare earth resources and their green extraction [M]. Beijing: Chemical Industry Press, 2014. (in Chinese)
[27] SOKOLOVA T A, ALEKSEEVA S A. Adsorption of sulfate ions by soils (A review) [J]. Eurasian Soil Science, 2008, 41(2): 140-148.
[28] SAUTY J P. An analysis of hydrodispersive transfer in aquifers [J]. Water Resources Research, 1989, 16(1): 145-158.
[29] STEEFEL C I, MACQUARRIE K T B. Approaches to modeling of reactive transport in porous media [J]. Reactive Transport in Porous Media, 1996, 34(5): 83-125.
[30] WALTER A L, FRIND E O, BLOWES D W, PTACEK C J, MOLSON J W. Modeling of multicomponent reactive transport in groundwater: 1. Model development and evaluation [J]. Water Resources Research, 1994, 30(11): 3137-3148.
[31] CLEMENT T P, SUN Y, HOOKER B S, PETERSEN J N. Modeling multispecies reactive transport in ground water [J]. Ground Water Monitoring and Remediation, 2010, 18(2): 79-92.
龙 平1,2,王观石3,田 君1,4,胡世丽3,罗嗣海3
1. 江西理工大学 资源与环境工程学院,赣州 341000;
2. 江西理工大学 江西省离子型稀土资源高效开发及应用协同创新中心,赣州 341000;
3. 江西理工大学 建筑与测绘工程学院,赣州 341000;
4. 江西省科学院 应用化学研究所,南昌 330029
摘 要:通过杯浸试验确定浸矿的离子交换模型为Kerr模型,得到Kerr模型的选择系数为12.59×10-10 L2/g2;采用对流-弥散方程描述柱浸过程铵根离子和稀土离子的运移规律,通过Kerr模型确定对流-弥散方程中的源汇项,运用顺序非迭代法解具有强非线性的对流-弥散方程,模拟稀土离子在土柱中的运移过程。与室内一维柱浸试验稀土离子的穿透曲线进行比较,两者的相关系数达到0.8724,说明本方法可以较为准确地模拟风化壳淋积型稀土矿一维柱浸过程。分析硫酸铵溶液浓度对稀土浸取率的影响,结果发现,最优硫酸铵溶液浓度( )与稀土品位(η)满足线性关系。
)与稀土品位(η)满足线性关系。
关键词:风化壳淋积型稀土矿;柱浸;离子交换;溶质运移
(Edited by Bing YANG)
Foundation item: Projects (51664015, 41602311, 51774156) supported by the National Natural Science Foundation of China
Corresponding author: Guan-shi WANG; E-mail: wgsky010@126.com
DOI: 10.1016/S1003-6326(19)64972-1

