基于旋量理论的弹性关节六腿机器人动力学分析
丁希仑，李可佳，徐坤
(北京航空航天大学 机械工程与自动化学院，北京，100191)
摘要：分析了关节弹性变形对六腿机器人运动产生的影响，采用旋量理论对六腿步行机器人的位置、速度和能量进行了描述，并应用拉格朗日方程建立了简洁、完整的六腿步行机器人的动力学模型。仿真对比实验结果说明了恒定的关节弹性变形、时变的关节弹性变形、关节的运动速度对六腿机器人抬起腿和支撑腿输出力矩的影响程度。
关键词：六腿机器人；动力学；弹性关节；旋量
中图分类号：TP242 文献标志码：A 文章编号：1672-7207(2011)S1-0589-07
Dynamics analysis of six-legged robot with elastic joints using screw theory
DING Xi-lun, LI Ke-jia, XU Kun
(School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics,
Beijing 100191, China)
Abstract: Six-legged robot’s dynamics was analysized considering joint elasticity, the position and velocity, and energy caused by joints’ flexible variable based on the screw theory were described in detail. The compact and complete Lagrange equation of the six-legged robot system was established. The influence of elastic joints’ deformation on the lifting legs was demonstrated and supporting legs by inverse dynamics simulation with constant and time-varying joint elasticity were demonstrated, moreover the effect of joints’ speed was illustrated. The results of simulation reveal the influence of dynamics model caused by joint elasticity.
Key words: six-legged robot; dynamics; elastic joint; screw
为了使步行机器人能够在高低不平的地面上完成未知环境探测及搬运等工作，需要在机器人的控制系统中加入前馈控制，而机器人的动力学模型是实现前馈控制的关键。机器人动力学方程反映了机器人运动轨迹、速度、加速度、接触力与关节驱动力之间的关系，它对机器人的机构设计、运动控制及仿真起到重要的作用。目前，关于步行机器人的动力学研究已经取得了不少成果。Zanganeh等[1]采用自然正交补集方法建立了固定基座六腿并联机器人的动力学模型；Pedro等[2]用自由体图方法建立了六腿步行机器人的运动学和动力学方程，该方法降低了动力学建模的难 度；Zhao等[3]用运动影响系数和虚功原理进行了机器人动力学建模，提出了2个用来分析步行机器人工作空间的动态指数；Bowling[4]将步行机器人当作浮动的多刚体系统，忽略关节内摩擦建立了多腿机器人的动力学方程并对其动态性能进行了分析；Featherstone[5]提出了描述机器人运动的空间矢量法和复合刚体动力学算法，简化了动力学方程的复杂程度。但是，现有的相关研究成果几乎均假设机器人的转动关节是理想刚体，不考虑其弹性变形，或者将关节弹性变形当作外力变量，未对其进行求解。然而，步行机器人，因受其自身重力和负载的影响，腿部各关节承受很大应力，存在一定程度上的弹性变形，忽略这点必将降低动力学模型准确性。本文作者分析了关节弹性变形对机器人的抬起腿、支撑腿及机器人身体的影响，应用旋量理论简洁地描述了机器人各个构件的位置、速度和能量，利用拉格朗日方法建立了完整的六腿步行机器人动力学模型，仿真结果反映了关节弹性变形对关节输出力矩的影响。
1 六腿机器人弹性腿的刚度表达
六腿步行机器人的机械结构如图1所示，该机器人由半球形身体和对称分布的6条腿组成。每条腿均包含髋关节、大腿、膝关节、小腿和足，具有3个自由度(髋关节2个、膝关节1个)。定义负责大腿抬起的关节为纵摆髋关节，负责腿转动的关节为横摆髋关节。
采用该结构机器人的灵活性高，并且具有较强的容错能力。它可以采用3条腿支撑、3条腿抬起的(3+3)昆虫步态、哺乳动物步态及混合步态行走；当其中的1条或2条腿当作机械臂使用或者有腿损坏时，采用5条腿支撑的5+1步或4条腿支撑的4+2步态行走[6]。
在机器人身体的圆形底盘中心建立笛卡尔坐标系ObXbYbZb，在每条腿的足端和各个关节处建立坐标系 jOi jXi jYi jZi，(j=1, 2, …, 6；i=0, 1, 2, 3)。其中j为腿号，i从0到3分别代表足端、膝关节、纵摆髋关节、横摆髋关节。
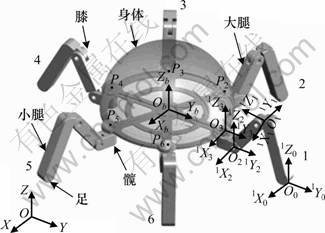
图1 六腿机器人结构简图
Fig.1 Structure of six-legged robot
机器人的任意一个转动关节i都存在一定的弹性变形，其主要部分是沿旋转轴的转角误差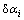
。导致关节产生弹性变形的力矩和弹性势能分别为：
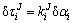(1)
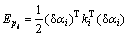(2)
其中：ki为刚度系数；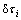
和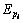
分别为与关节弹性变形相对应的力矩变化和弹性势能。
机器人在行走过程中，各条腿按照一定规律抬起、转动、落下，每条抬起腿可以看作是以机器人身体为基座的串联机器臂；各条支撑腿、机器人身体和地面所构成的整体可以等价为一个并联平台进行分析。
对于具有n个弹性关节的抬起腿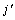
来说，关节弹性变形对应的力矩变化
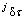及弹性势能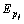
分别为：
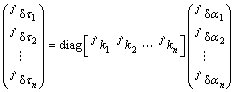(3)
式(3)可以简写成：
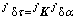(4)
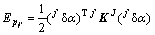(5)
其中：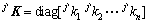
为该腿的刚度矩阵。关节的微小转角可以看作为运动旋量s，与其对应的力旋量
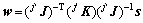，其中
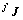为腿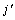的雅克比矩阵[7]。因此，刚度矩阵可以表示为一个6×6的对称阵：
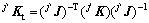(6)
2 六腿机器人系统的刚度分析
前面对六腿机器人的单个关节及抬起腿的关节弹性变形引起的力矩和势能进行了分析，这里主要阐述支撑腿的关节弹性变形对机器人系统产生的影响，为此需要求解并联机器人系统的刚度系数。
假设机器人在行走过程中没有滑移，身体底盘与地面平行，则足端与地面的接触为一个两自由度转动铰链(机器人小腿可绕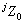
和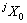
转动)。将机器人的身体分解，则每条支撑腿可以看作是以足端为基座，机器人身体为末端的串联机器人。
机器人身体的刚度与支撑腿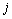
的刚度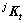
有关，但每条腿的刚度是建立在各自的坐标系
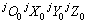中，为求解并联平台的总刚度Kp需要对
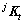进行坐标变换。
由于关节弹性变形值很小，可以将其当做速度处理。设支撑腿j与身体的连接点Pk在足端坐标系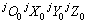中的运动旋量为
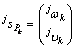，则它在基坐标中可以描述为：
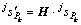(7)
其中：
；
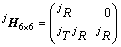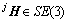是刚体从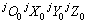到基坐标系OXYZ的变换矩阵；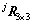
是旋转矩阵；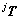
是平移向量t的反对称阵，对于任意一个3维向量x总能得到
。
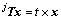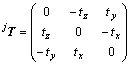(8)
根据式(6)可知支撑腿j在各自坐标系中的刚度矩阵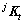，j=1, 2, …, n。将其进行坐标变换，把各个刚度矩阵转化到基坐标系中表达：
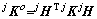；j=1, 2, …, n (9)
因此，具有n条支撑腿的机器人系统在基坐标系中的总刚度Kp为：
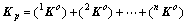(10)
3 考虑关节弹性的动力学模型
以六腿机器人沿腿1方向采用3+3混合步态行走为例，如图2所示，建立机器人行走的运动方程。设机器人身体的质心位于底盘圆心Ob处，腿部各构件的质心均位于几何中心位置。并已知各个关节的转动变量和弹性变形，采用旋量理论对机器人身体、抬起腿及支撑腿的位置及运动进行描述，建立机器人系统的动能及势能的表达式，应用拉格朗日方法求解机器人各关节的输入力矩。
3.1 系统动能
机器人的系统动能包括6条腿的动能及机器人身体的动能。已知各足端在机器人身体坐标系ObXbYbZb中的运动轨迹，通过逆运动学可以求解得到任意腿的膝关节、纵摆髋关节、横摆髋关节的转角变量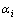
(i=1, 2, 3)。设各个关节弹性变形为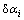(i=1, 2, 3)。
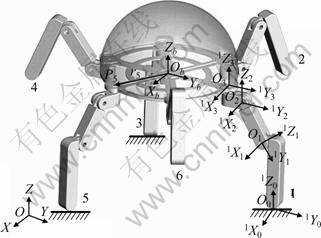
图 2 六腿机器人3+3混合步态行走
Fig.2 Mixed gait of six-legged robot
机器人身体的运动是由支撑腿的协调运动实现的，采用3+3混合步态行走时，身体始终与地面保持平衡，没有仰俯和侧倾等摆动。其速度可由连接点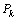
在坐标系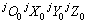中的运动旋量
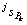求得。由于支撑腿看作是以足端为基座、机器人身体为末端的串联机器人，因此，当机器人身体底盘与地面平行时可以将支撑腿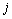的3个关节转角分别转化为小腿绕Z0的转角
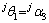，绕X0的转角
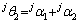，膝关节转角
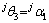。各关节弹性变形分别为
，
，
。
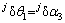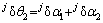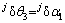在坐标系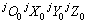中建立支撑腿j的运动学方程，设腿j与身体的连接点
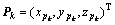(k=j)转动后的新位置为
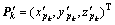，则
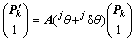(11)
其中：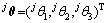
；
；
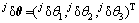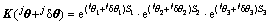，为支撑腿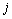的坐标变化。
将式(11)对时间t求导可得点Pk的运动速度：
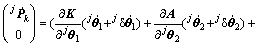
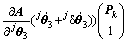(12)
假设初始位置时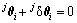
(i=1, 2, 3)，可得各偏导数在初始位置的值：
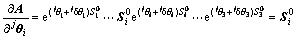(13)
这个关系具有一般性，当定义一个关节运动旋量的初始位置为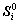
时，由共轭运算可得其当前的位 置[8]，
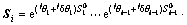
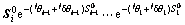(14)
将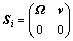
转换成六维向量形式Si表达，就可以得到髋关节与身体连接点Pk的运动旋量
，
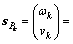
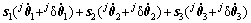(15)
式(15)可以简写成：
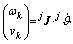(16)
其中：
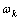和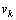
分别为该点的角速度和线速度，
；
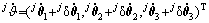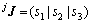,为支撑腿j的雅可比矩阵。
根据以上结果可求得机器人身体在足端坐标系中的速度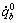
：
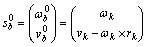(17)
其中：
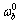和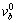
分别为机器人身体的角速度和线速度；rk为质心Ob到Pk的三维矢量。由于接触点在刚体上，因此，各接触点与动平台质心的角速度相同，即
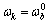。根据式(7)，
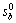在基坐标中可以描述为：
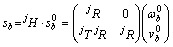(18)
因此，机器人身体的动能为：
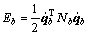(19)
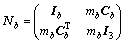(20)
其中：机器人身体的惯性矩阵为Nb；mb为质量；I3为3×3单位矩阵。在基坐标系中，机器人身体的质心位置由3×3反对称矩阵Cb表示，转动惯量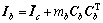
；
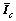为身体相对质心的转动惯量[5]。
设机器人腿j的膝关节、纵摆髋关节和横摆髋关节连接的各杆重心的运动旋量分别为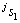
，
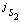和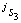
，则腿j的动能为：
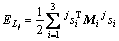；j=1, 2, …, 6 (21)
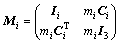(22)
式中：Mi和mi分别为惯性矩阵和质量(i=1，表示膝关节；i=2，表示纵摆髋关节；i=3，表示横摆髋关节)；Ci为质心位置的3×3反对称矩阵；转动惯量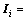
；
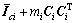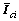为构件相对各自质心的转动惯量。
至此，由式(19)和(21)可求得系统总动能为：
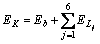(23)
3.2 系统势能
在基坐标系中，系统的势能包括各个刚体的重力势能、机器人系统及抬起腿各关节的弹性势能。
机器人系统的弹性势能与支撑腿关节的弹性变形有关。由于关节弹性变形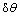
很小，可以将其当作速度处理。根据式(16)可求得支撑腿与机器人身体接触点Pk在坐标系
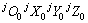中的位移变量
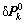及机器人身体在基坐标系下的位移变量
：
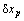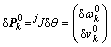(24)
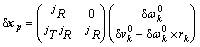(25)
任意一条抬起腿3个关节产生的弹性势能可由式(5)求得。因此，抬起腿为2，4和6时，机器人系统的总势能为：
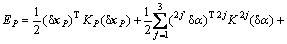
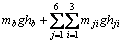(26)
其中：hb和hji分别为机器人身体及腿上各构件在基坐标系中的高度。
3.3 动力学方程
应用牛顿欧拉方法建立的动力学方程对于解决动力学正问题是比较有效的，但是，要消除约束反力建立闭式的动力学方程进行逆动力学计算比较困难，采用拉格朗日方程相对而言更容易[9]。设拉格朗日函数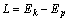
，则当抬起腿2，4和6以及支撑腿1，3和5时机器人的动力学方程分别为：
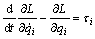; i=2, 4, 6 (27a)
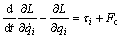; i=1, 3, 5 (27b)
其中：qi为广义坐标，即机器人抬起腿上各个关节的转动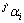变量
及弹性变量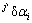
，支撑腿上各个关节的转动变量
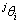及弹性变量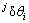
；Fc为机器人身体各部分之间的约束力。当抬起腿和支撑腿切换以后，式(27)中的腿号互换。
4 机器人3+3混合步态行走动力学 仿真
机器人的3+3混合步态行走如图2所示。假设机器人沿腿1的方向行走，则腿1和4的横摆髋关节没有绕Z轴的运动。本节对该步态行走机器人的支撑腿1和抬起腿4进行逆动力学计算仿真。通过计算结果分析不同关节弹性变形对各条腿输出力矩的影响。
令机器人身体质量mb=6 kg,大腿及小腿的质量m1=m2=1 kg，质心均在各构件的几何中心，重力加速度g=9.81 N/kg，忽略髋关节质量。机器人身体半径R、大腿长度l1、小腿长度l2均为1 m。
4.1 抬起腿考虑关节弹性变形的关节力矩变化
设腿中4条大腿的初始位置与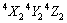
坐标系的Y2轴夹角为
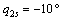，终止位置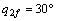
；小腿的初始位置与Y2轴夹角
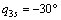，终止位置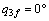
，运行时间Tp=15 s，关节的运动轨迹q1n和q2n为：
；
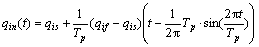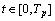；i=1, 2 (28)
取关节弹性变形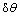分别为
，
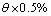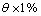和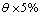
进行计算，其中
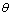为腿4各关节的转角。腿4纵摆髋关节力矩如图3所示，其中：实线4为不考虑关节弹性变形时腿4纵摆髋关节按规定轨迹运动的力矩输出值情况，其余3条曲线分别为不同弹性变形值对应的力矩。从图3可以看出：受到弹性变形影响的3条力矩输出曲线与不考虑弹性变形情况下的力矩曲线相比，在任何时刻都存在误差，但是，曲线整体变化趋势是一致的。当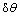≤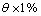时，与不考虑关节弹性变形相比，力矩的差值在0.2 N·m内，误差较小，力矩的变化幅度小于1.1%；当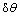=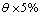时，误差大约为1 N·m，力矩的变化幅度约为5.4%，力矩输出误差明显。
图4所示为腿4膝关节的输出力矩变化情况，各条曲线的变化趋势几乎一致，但是，由于该关节只受小腿质量的影响，弹性变形对其力矩输出的影响不如对纵摆髋关节的影响大；当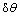≤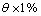时，与不考虑关节弹性变形相比力矩的差值在0.04 N·m内，力矩的变化幅度小于0.9%；当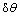=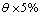时，误差大约为0.15 N·m，力矩的变化幅度约为3.5%。
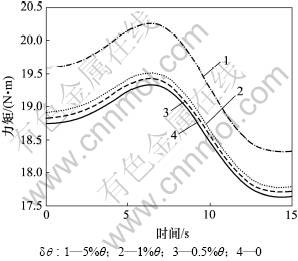
图3 腿4纵摆髋关节力矩
Fig.3 Torque of hip pitching joint of leg 4
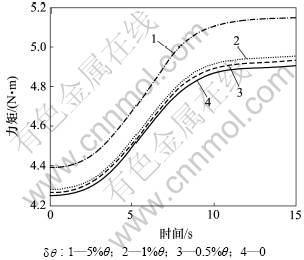
图4 腿4膝关节力矩
Fig.4 Torque of knee joint of leg 4
4.2 支撑腿考虑关节弹性变形及关节转动速度的关节力矩变化
本节对支撑腿1的膝关节分别对恒定的弹性变形、时变的弹性变形及机器人不同速度情况下关节力矩进行计算和分析。
与抬起腿不同，支撑腿受到机器人身体和抬起腿的重力作用，关节力矩远大于抬起腿的相应关节力矩。设腿1的大腿初始位置与1X21Y21Z2坐标系的Y2轴夹角为q2s=-30°，运动终止位置与Y2轴夹角为q2s=-10°；小腿的初始位置与1X21Y21Z2坐标系中Y2轴的夹角为q3s=-60°，终止位置q3s=-90°，运行时间Tp=15 s，关节运动轨迹同样为式(28)。
首先，分别以关节弹性变形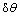为，
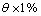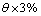和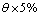
，计算支撑腿1的膝关节力矩。3条支撑腿的膝关节需要承担机器人身体、3条抬起腿以及支撑腿大腿的重力，同时还要为机器人行走提供动力。在给定的初始位置，膝关节输出力矩最大为-26.95 N·m；当运动结束时小腿与地面垂直时，此时膝关节的力矩为0，如图5所示。当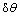≤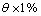时，与不考虑关节弹性变形的情况相比力矩的差值在1 N·m内，力矩的变化幅度小于3.7%；当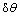=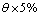时，误差大约为2.5 N·m，力矩的变化幅度约为9.3%。与图4相比，在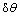相同的情况下，支撑腿关节的力矩变化明显大于抬起腿关节的力矩变化。
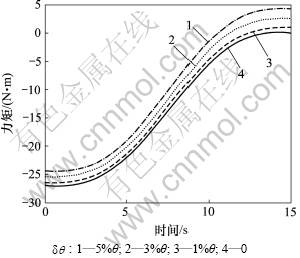
图5 在关节弹性变形恒定的条件下腿1膝关节的力矩
Fig.5 Torque of knee joint of leg 1 under condition of constant deofrmation
其次，对支撑腿膝关节在关节弹性变形随时间变化情况下的力矩输出进行分析。取以下4种情况分别进行计算：
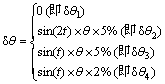
计算结果如图6所示。其中：实线同样为不考虑关节弹性变形时腿1膝关节按规定轨迹运动的力矩输出值情况，其余3条为关节弹性变量随不同的变化周期和幅值而变化的力矩输出曲线。将整个仿真过程分为初始(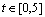
)、中间(
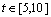)及终止(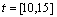
)3个阶段，由图6可以看出：在初始和终止阶段，力矩的输出受到关节弹性变形的影响大；中间阶段由于力矩变化较快，弹性变形对其的影响较小。对比3条虚线不难发现振幅越大、频率越高的关节弹性变形对力矩的输出结果影响就越大，这一结论与理论预判是一致的。
最后，对机器人的运动速度与支撑腿关节力矩变化的关系进行分析。同样以式(28)的运动轨迹为例，分别取运行时间Tp为5，10，15和20 s进行计算，结果如图7所示。可见：在4种不同速度下，支撑腿膝关节的初始及终止时刻的力矩相同，但是，力矩的变化速率各不相同，速度越快，力矩变化越快；Tp=20 s时曲线的斜率大约为Tp=5 s时曲线斜率的一半。力矩变化越快对电机及传动齿轮的影响就越大。因此，为了保护机器人、延长其使用寿命，应该将关节的转速控制在一定范围以内。
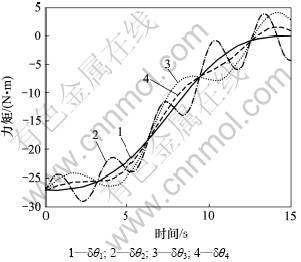
图6 在关节弹性变形时变的条件下支撑腿1膝关节的力矩
Fig.6 Torque of knee joint of leg 1 under condition of deformation varying with time
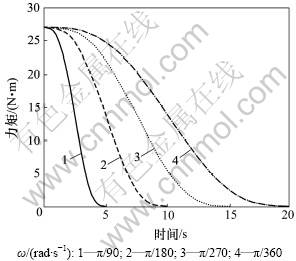
图7 不同速度下运支撑腿1膝关节力矩输出对比
Fig.7 Torque of knee joint of leg 1 with different velocities
5 结论
对六腿步行机器人进行了动力学分析。着重分析了关节弹性变形对机器人动力学的影响。采用旋量理论对机器人的各个杆件位置、速度及能量进行了描述，建立了六腿机器人完整的拉格朗日方程。针对六腿机器人3+3混合步态行走进行的仿真实验说明了不同程度(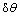=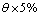)、恒定的关节弹性变形对于抬起腿和支撑腿关节产生的不同影响。同时，对关节弹性变形随时间变化情况下的力矩输出变化进行了计算仿真，结果说明关节变量变化的振幅与频率对输出力矩的影响。此外，还以支撑腿膝关节为例分析了机器人不同运动速度下关节输出力矩的变化情况。关节弹性变形对六腿机器人动力学模型具有重要作用。
参考文献：
[1] Zanganeh K E, Rosario S, Jorge A. Kinematics and dynamics of a six-degree-of-freedom parallel manipulator with revolute legs[J]. Robotica, 1997, 15(4): 385-394.
[2] Pedro B J,Trigo A, Menezes P, et al. FBD-the Free Body Diagram method. Kinematic and dynamic modeling of a six leg robot[C]//International Workshop on Advanced Motion Control. Coimbra, Portugal, 1998: 423-428.
[3] ZHAO Yong-sheng, LU Ling,ZHAO Tie-shi, et al. Dynamic performance analysis of six-legged walking machines[J]. Mechanism and Machine Theory, 2000, 35(1): 155-163.
[4] Bowling A P. Dynamic performance, mobility, and agility of multilegged robots[J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 2006, 128(4): 765-777.
[5] Featherstone R. Rigid body dynamics algorithms[M]. Berlin, Heidelberg: Springer, 2007: 31-60.
[6] WANG Zhi-ying, DING Xi-lun, Rovetta A. Analysis of typical locomotion of a symmetric hexapod robot[J]. Robotica, 2010, 28(6): 893-907.
[7] DING Xi-lun, Selig J M. Screw theory on spatial stiffness analysis of robots with elastic joints and links[J]. Chinese Journal of Mechanical Engineering: English Edition, 2004, 17(Suppl): 248-252.
[8] Selig J M, Ding Xi-lun. A screw theory of static beams[C]//Proceedings of IEEE/IROS. Maui, Hawaii, 2001: 312-317.
[9] 赵锡芳. 机器人动力学[M]. 上海: 上海交通大学出版社, 1992: 15-22.
ZHAO Xi-fang. Robot dynamics[M]. Shanghai: Shanghai Jiaotong University Press, 1992: 15-22.
(编辑 陈灿华)
收稿日期：2011-04-15；修回日期：2011-06-15
基金项目：国家“863”计划项目(2006AA04Z207)
通信作者：李可佳(1982-)，男，黑龙江齐齐哈尔人，博士研究生，从事机器人动力学研究；电话：010-82339055；E-mail: likejia5@gmail.com
