基于响应面方法的车辆多目标协同优化
刘士士1,谷正气1,伍文广1,米承继1,梁小波2,彭国谱2
(1. 湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082;
2. 湘电重型装备股份有限公司,湖南 湘潭,411100)
摘要:建立包含7个子系统的某整车动力学仿真模型,以整车的操纵稳定性和行驶平顺性达到最佳匹配为目标,整车的悬架刚度和减震器的阻尼以及稳定杆的扭转刚度为优化变量,在ADAMS/CAR环境下进行仿真。根据中国汽车行业标准QC/T 480—1999和GB/T 4970—2006,分别以操纵稳定性的4个闭环评价指标和平顺性的随机路面评价指标的综合计分为目标函数,以相应计分的最大、最小值作为约束函数建立协同优化的数学模型。然后采用中心复合试验方法设计59组试验,根据实验数据,运用响应面方法(RSM)拟合出回归模型,得到最优值。仿真结果表明该优化方法使汽车的综合计分提高了13%,操纵稳定性和平顺性同时得到优化。
关键词:操纵稳定性;平顺性;协同优化;响应面方法
中图分类号:TP391.9 文献标志码:A 文章编号:1672-7207(2012)07-2586-07
Multi-objective collaborative optimization of vehicle based on response surface methodology
LIU Shi-shi1, GU Zheng-qi1, WU Wen-guang1, MI Cheng-ji1, LIANG Xiao-bo2, PENG Guo-pu2
(1. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China;
2. Xiangtan Electric Manufacturing Group Heavy-duty Equipment Co. Ltd, Xiangtan 411100, China)
Abstract: The full vehicle dynamics virtual prototype which included 7 subsystems was established to simulate using ADAMS/CAR, with the best match between handling stability and the ride comfort performance of the car as the object, taking the stiffness and damping of the suspension, the torsion stiffness of anti-roll bar as the optimization variables. According to the Chinese automotive industry standard QC/T 480—1999 and GB/T 4970—2006, it built the corresponding mathematic model of collaborative optimization which used the total score of the comprehensive evaluation indexes include of the four closed-loop handling stability and ride comfort evaluation of random road as the objective function, used the maximum or the minimum score as a constraint function. Then 59 groups test was designed using central composite test method and the total score was estimated by using response surface methodology (RSM). Optimization result of design factors shows that the total score of the full vehicle improves by 13%, and handling stability and the ride comfort performance both are improved.
Key words: handling stability; riding comfort; collaborative optimization; RSM
车辆的悬架系统是影响操纵稳定性和行驶平顺性的关键部件,操纵稳定性和行驶平顺性又是评价汽车整体性能的重要指标。近年来,国内外在操纵稳定性和行驶平顺性方面已经开展了不少研究[1-8]。然而车辆的操纵稳定性和行驶平顺性之间存在着耦合变量,单纯基于某一项性能的优化往往会导致另一性能的降低。因此,单目标优化方法或是基于某一性能的多目标优化的方法,未能考虑二者的耦合关系。鉴于此,文中采用一种能同时使车辆的操纵稳定性和行驶平顺性达到最佳匹配的协同优化的方法,该方法是一种典型的多学科设计方法,可以将车辆的操纵稳定性和行驶平顺性的各项指标进行多目标的平衡和优化。本文作者用ADAMS/CAR软件建立了完整的整车模型,在优化过程中选用协同优化的响应面算法作为优化方法。响应面方法是在试验的基础上考虑其随机误差,同时将复杂未知的函数关系在小区域内用简单的一次或二次多项式来拟合,计算较简单[9-10]。由于响应面方法是以试验为基础,因此,试验设计的合理性直接影响了优化的准确性和效率,采用中心复合理论进行试验设计,大大提高了优化效率,使汽车的操纵稳定性和平顺性同时得到提高。
1 整车模型的建立和评价指标
本文所研究的模型是在Adams/CAR软件中建立的动力学整车模型。该模型共有135个自由度[11],分为7个子系统,建模时,先分别建立各个子系统的模型,然后在子系统间建立通信端口命令,最后装配成整车模型。模型的前悬架采用双横臂独立式悬架,后悬架为多连杆独立悬架,转向系为齿轮齿条转向系,制动器为四轮盘式制动器,底盘为去掉车身几何体的刚性底盘,前后轮胎型号均为205/50R17。所建的动力学模型如图1所示,建模中需要的重要参数如表1所示。
鉴于汽车系统的复杂性,建模时进行了如下适当的简化[12-13]。
(1) 除轮胎、阻尼元件、弹性元件及橡胶元件外,其余构件均作为刚体,忽略其变形;

图1 整车动力学模型
Fig.1 Vehicle dynamics model
(2) 对于刚体之间的柔性连接作适当的简化,用线性弹性橡胶衬套来模拟实际工况下的动力学特性,且对于理想铰链,除转动副和滑动副之外各运动副的摩擦力均忽略不计。
整车动力学模型建立后,常需要对模型进行试验验证,本文采用文献[1]介绍的方法对该模型进行验证,验证结果说明文中的建模方法是可行的,并具有较高的准确度,可以用来进行整车性能预测分析。
汽车的操纵稳定性能是指在驾驶者不感到过分紧张、疲劳的条件下,汽车能遵循驾驶者通过转向系及转向车轮给定的方向行驶,且当遭遇外界干扰时,汽车能抵抗干扰而保留稳定行驶的能力。操纵稳定性是影响汽车主动安全的重要性能之一。
汽车操稳性的评价方法很多,一般包括开环和闭环两种评价方法。在汽车动力学软件中,操纵稳定性的评价方法可根据中国汽车行业标准QC/T 480—1999,通过几种典型的行驶工况来模拟典型驾驶操纵的通道性能,这些典型行驶工况是从汽车实际行驶中选取的,评价比较接近于实际交通情况,因此能如实地反映汽车的操纵稳定性。该标准规定的汽车稳定性的评价指标如下:
(1) 转向瞬态响应试验(转向盘转角阶跃输入) 仿真试验按照侧向加速度为2 m/s2时的汽车横摆角速度的响应时间t进行评价计分。汽车横摆角速度响应时间的评价计分按下式计算:
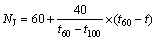 (1)
(1)
式中:NJ,t60,t100和t分别为横摆角速度响应时间的计分值、下限值、上限制和试验值。
表1 整车建模主要参数
Table 1 Main parameters of vehicle model

(2) 转向瞬态响应试验(转向角转角脉冲输入) 仿真试验按照相位滞后角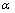 进行评价计分。相位滞后角的评价计分按下式计算:
进行评价计分。相位滞后角的评价计分按下式计算:
 (2)
(2)
式中: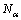 ,
,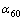 ,
,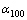 和
和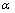 分别为相位滞后角的评价计分值、下限值、上限制和试验值。
分别为相位滞后角的评价计分值、下限值、上限制和试验值。
(3) 蛇形试验。仿真试验按照基准车速(65 km/h)下的平均横摆角速度峰值γ进行评价计分,平均横摆角速度峰值的评价计分按下式计算:
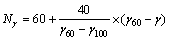 (3)
(3)
式中: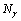 ,
,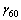 ,
,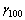 和
和 分别为平均横摆角速度峰值的计分值、下限值、上限制和试验值。
分别为平均横摆角速度峰值的计分值、下限值、上限制和试验值。
(4) 转向回正试验。仿真试验按照松开转向盘3 s时的残留横摆角速度的绝对值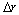 进行评价计分,残留横摆角速度的绝对值评价计分按下式计算:
进行评价计分,残留横摆角速度的绝对值评价计分按下式计算:
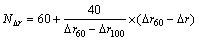 (4)
(4)
式中: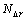 ,
,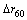 ,
, 和
和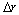 分别为残留横摆角速度绝对的评价计分值、下限值、上限制和试验值。
分别为残留横摆角速度绝对的评价计分值、下限值、上限制和试验值。
汽车平顺性主要是保持汽车在行驶过程中产生的振动和冲击环境对乘员舒适性的影响在一定界限之内,因此平顺性主要是根据乘员主观感觉的舒适性来评价。由于要对所建车型进行多目标的协同优化,考虑操纵稳定性的同时也要考虑平顺性,故构建加权加速度均方根值的评价计分值,评价标准同操稳一样,评价计分值越大越好。行驶平顺性随机输入试验评价计分可通过下式计算:
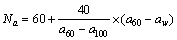 (5)
(5)
式中:Na,a60,a100和aw分别为随机输入试验的评价计分值、下限值、上限制和试验值。
2 协同优化的响应面算法
中国汽车行业标准QC/T 480—1999中规定,汽车操纵稳定性的评价按照各项指标的评价计分数大小来衡量,评价计分数小于60分的为不及格,大于100分的按照100分来计算。为了便于进行优化,将5个评价指标做如下替换:
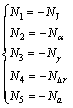 (6)
(6)
所构建的协同优化的系统级数学模型如下:
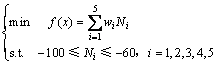 (7)
(7)
式中:f(x)为多目标的优化函数值;Ni为各个子目标的计分值,可通过仿真试验获得;wi为第i项目标函数的权因子,主要表示各子目标函数重要程度。文中进行研究时将5个子目标函数看作同等重要,所以有wi=1 (i=1, 2, 3, 4, 5)。
悬架系统是影响整车性能的主要因素,而悬架的结构参数和性能参数对汽车的操纵稳定性和行驶平顺性有很大的影响。因此,根据文献[2, 13],通过影响汽车操纵稳定性和行驶平顺性的灵敏度分析,作者把前后悬架的刚度和减震器的阻尼以及横向稳定杆的扭转刚度作为操纵稳定性和平顺协同优化的变量(假设弹簧和减震器是左右对称的)。这6个优化变量是对整车的操纵稳定性和行驶平顺性影响最大的因素,为了便于仿真计算,将优化变量分别乘以一个比例因子来改变其大小。考虑到文中是在基本确定的模型上进行的优化,所以选定各优化变量的范围为±50%,设计变量见表2。
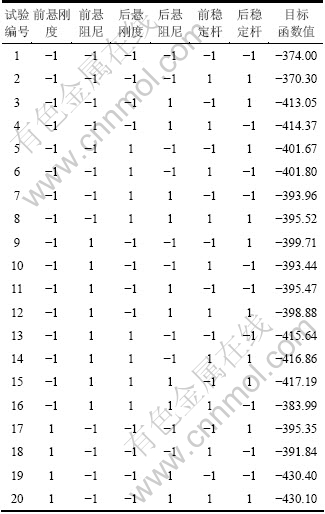
文中有优化变量6个,优化目标5个,因此二阶响应曲面模型的回归系数共有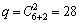 个。为了得到回归方程,每个因子所取的水平应大于或等于3,因而所要做的试验次数是很多的,文中变量有6个,如果做3水平全因子试验,就需要做729次试验。而试验次数之大,很难实现,中心复合试验设计就是为了解决这一矛盾而提出的一种设计试验的方法,因此文中选用中心复合设计来设计试验,并进行回归设计。作者将各个设计变量正规化,设它们的最大值均为1,最小值均为-1,各个变量具有交互作用。根据文献[14]经过计算分析,该文需进行32次二水平部分试验,15次中心点试验和12次轴向点试验,共59次试验。安排好试验次数,根据1.1节在ADAMS/CAR中建立的整车模型,编写5个优化目标的驱动控制文件及相应工况的路面进行优化仿真,得到评价指标的计分值。部分试验安排和仿真结果如表3所示。
个。为了得到回归方程,每个因子所取的水平应大于或等于3,因而所要做的试验次数是很多的,文中变量有6个,如果做3水平全因子试验,就需要做729次试验。而试验次数之大,很难实现,中心复合试验设计就是为了解决这一矛盾而提出的一种设计试验的方法,因此文中选用中心复合设计来设计试验,并进行回归设计。作者将各个设计变量正规化,设它们的最大值均为1,最小值均为-1,各个变量具有交互作用。根据文献[14]经过计算分析,该文需进行32次二水平部分试验,15次中心点试验和12次轴向点试验,共59次试验。安排好试验次数,根据1.1节在ADAMS/CAR中建立的整车模型,编写5个优化目标的驱动控制文件及相应工况的路面进行优化仿真,得到评价指标的计分值。部分试验安排和仿真结果如表3所示。
表2 设计变量初始值的取值范围
Table 2 Range of design variables’ initial value

表3 基于中心复合试验的部分试验设计
Table 3 Part design based on central composite experimental
文中的设计变量有6个,其近似模型见式(8),其中: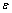 为随机误差,服从正态分布,其均值为零,方差为
为随机误差,服从正态分布,其均值为零,方差为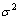 。
。
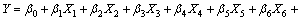
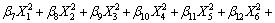
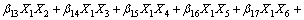
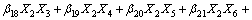
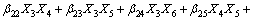
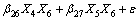 (8)
(8)
根据实验结果,获得在不同变量xi的水平值组合下的系统响应值yi,用二次多项式模拟作为输入和输出的实际函数的近似,根据最小二乘法原理对这些数据进行拟合。
二阶响应面的回归系数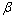 的最小二乘估计值是:
的最小二乘估计值是:
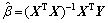 (9)
(9)
得到回归模型为:

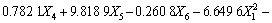
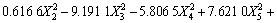
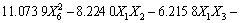
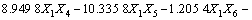

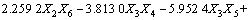
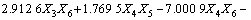
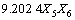 (10)
(10)
采用响应面方法进行优化时,需要对拟合的响应面模型进行检验。作者采用二阶统计模型的显著性来检验该模型参数假设的正确性,计算可得此回归模型的回归平方和、误差平方和以及检验统计量等,表4所示为显著性方差分析参数表。
表4 显著性方差分析
Table 4 Significant analysis of variance
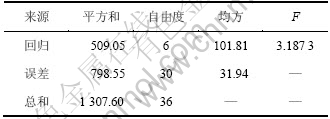
查表可得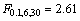 ,由于
,由于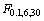 <F,因此该统计模型在显著性水平10%下是显著的,即该模型能较好地拟合仿真试验数据。
<F,因此该统计模型在显著性水平10%下是显著的,即该模型能较好地拟合仿真试验数据。
3 优化结果
通过拟合得出二次目标函数,运用MATLAB优化工具箱对目标函数在可行域内进行优化,使该函数取得最小值[15],图2和3所示为变量优化前后的阻尼曲线,表5所示为其数值变化,图4~8所示为试验中评价操纵稳定性和平顺性的性能曲线,表6所示为评价分。
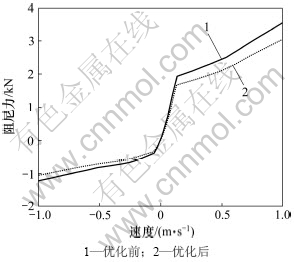
图2 优化前后前悬架阻尼曲线
Fig.2 Front suspension damping curves before and after optimization
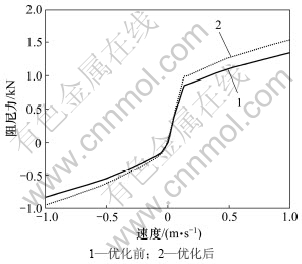
图3 优化前后后悬架阻尼曲线
Fig.3 Rear suspension damping curves before and after optimization
表5 优化前后参数变化量对比
Table 5 Parameter variation compared before and after optimization
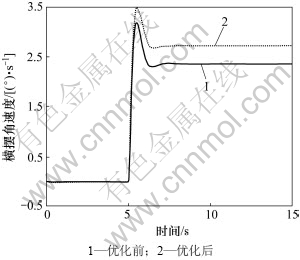
图4 优化前后转向盘角阶跃输入试验中横摆角速度曲线
Fig.4 Yaw rate curves of step input of steering wheel angle experiments before and after optimization
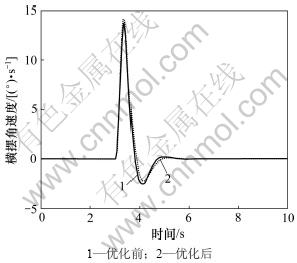
图5 优化前后转向角转角脉冲试验中横摆角速度曲线
Fig.5 Yaw rate curves of angle pulse of steering wheel angle before and after optimization
从仿真结果及其优化前后仿真图形对比可以看出,优化后操纵稳定性中的横摆角速度响应时间缩短,超调量也相应减少;平顺性性能中的车身质心位置的加权加速度均方根值比优化前减少5%左右。文中所采用的优化方法使汽车总的评价指标的计分提高了13%,操纵稳定性和平顺性同时得到优化。
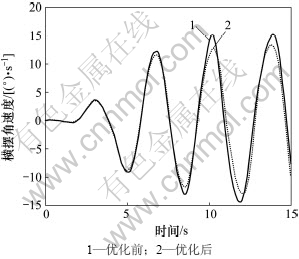
图6 优化前后蛇行试验中横摆角速度曲线
Fig.6 Yaw rate curves of hunting test before and after optimization
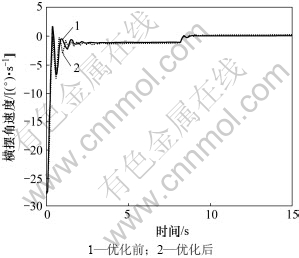
图7 优化前后转向回正试验中横摆角速度曲线
Fig.7 Yaw rate curves of steer-return test before and after optimization
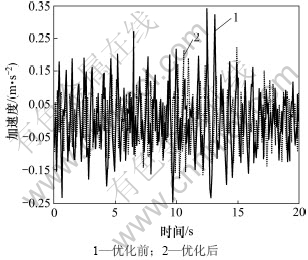
图8 优化前后平顺性B级随机路面车身垂向加速度曲线
Fig.8 Vertical acceleration of vehicle body curves of comfort test in B-class random road
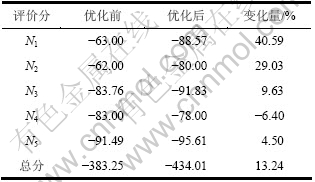
表6 优化前后评价分变化量
Table 6 Evaluation of changes in scores before and after optimization
4 结论
(1) 利用ADAMS/CAR软件建立整车刚柔耦合多体系统动力学模型,并运用中心复合实验设计理论,结合响应面方法拟合出二次响应面模型,得到的最优解使车辆的操纵稳定性和平顺性性能同时得到提高。
(2) 将协同优化的响应面算法用在整车操纵稳定性和平顺性优化中,所涉及的变量的选择和优化方法对其他类型车辆的设计和车辆其他性能的协同优化同样具有一定的参考价值。
参考文献:
[1] 海贵春. 某智能四驱SUV动力学性能分析与优化研究[D]. 长沙: 湖南大学机械与动载工程学院, 2008: 37-116.
HAI Gui-chun. Analysis and optimization of dynamic performance for a SUV[D]. Changsha: Hunan University. School of Mechanical and Vehicle Engineering, 2008: 37-116.
[2] 吕征, 谷正气, 李伟平, 等. 基于响应面方法的汽车操纵稳定性优化[J]. 系统仿真学报, 2009, 21(24): 7961-7968.
L? Zheng, GU Zheng-qi, LI Wei-ping, et al. Optimization of vehicle handing and stability based on RSM[J]. Journal of System Simulation, 2009, 21(24): 7961-7968.
[3] Sobieski J S, Kodiyalam S, Yang R Y. Optimization of car body under constrains of noise, vibration, and harshness(NVH), and crash[J]. Structural and Multidisciplinary Optimization, 2001, 22(4): 295-306.
[4] Uys P E. Criteria for handling measurement[J]. Journal of Terramechanics, 2006, 43: 43-67.
[5] Uys P E. Suspension settings for optimal ride comfort of off-road vehicles traveling on roads with different roughness and speeds[J]. Journal of Terramechanics, 2006, 18: 1-13.
[6] Craig K, Stander N, Dooge D, et al. MDO of automotive vehicle for crashworthiness and NVH using response surface methods[C]//The 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization. 2002: AIAA-2002-5607.
[7] 郑军. 新概念车操纵稳定性与舒适性研究[D]. 长沙: 湖南大学机械与运载工程学院, 2007: 52-110.
ZHENG Jun. On the ride comfort and handling characteristics of a new concept car[D]. Changsha: Hunan University. School of Mechanical and Vehicle Engineering, 2007: 52-110.
[8] 杨荣山, 袁仲荣, 黄向东, 等. 基于近似模型的车辆操纵稳定性及平顺性的优化研究[J]. 汽车技术, 2009(7): 18-22.
YANG Rong-shan, YUAN Zhong-rong, HUANG Xiang-dong, et al. Optimization and research on vehicle’s handling stability and ride comfort based on approximate model[J]. Automobile Technology, 2009(7): 18-22.
[9] 王娅, 谷正气, 李伟平, 等. 基于响应面方法的某智能SUV平顺性优化[J]. 机械科学与技术, 2010, 29(3): 373-379.
WANG Ya, GU Zheng-qi, LI Wei-ping, et al. Optimization of the ride comfort of an intelligent sport-utility vehicle(SUV)[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(3): 373-379.
[10] 陈立周. 机械优化设计方法[M]. 北京: 冶金工业出版社, 2005: 215-230.
CHEN Li-zhou. Mechanical optimum design[M]. Beijing: Metallurgical Industry Press, 2005: 215-230.
[11] 海贵春, 谷正气, 骆军, 等. 某SUV车稳态转向特性与优化[J]. 系统仿真学报, 2009, 21(7): 2068-2071.
HAI Gui-chun, GU Zheng-qi, LUO Jun, et al. Analysis and optimization of stable steering characteristic for SUV[J]. Journal of System Simulation, 2009, 21(7): 2068-2071.
[12] 陈黎卿, 陈无畏. 基于联合仿真技术的主动悬架自适应模糊PID控制研究[J]. 系统仿真学报, 2008, 20(5): 1340-1344.
CHEN Li-qing, CHEN Wu-wei. Study of active suspension adaptive fuzzy control based on co-simulation[J]. Journal of System Simulation, 2008, 20(5): 1340-1344.
[13] 王凯峰. 基于虚拟现实与虚拟样机的汽车操纵稳定性研究[D]. 合肥: 合肥工业大学机械与汽车工程学院, 2007: 28-29.
WANG Kai-feng. Research on vehicle handling stability based on virtual reality and virtual prototype[D]. Hefei: Hefei University of Technology. School of Mechanical and Automotive Engineering, 2007: 28-29.
[14] 任露泉. 试验优化设计与分析[M]. 2版. 北京: 高等教育出版社, 2003: 246-278.
REN Lu-quan. Optimum design and analysis of experiments[M]. 2nd ed. Beijing: Higher Education Press, 2003: 246-278.
[15] 苏金明, 阮沈勇, 王永利. Matlab工程数学[M]. 北京: 电子工业出版社, 2005: 73-83.
SU Jin-ming, RUAN Shen-yong, WANG Yong-li. Matlab engineering mathematics[M]. Beijing: Electronic Industry Press, 2005: 73-83.
(编辑 陈爱华)
收稿日期:2011-08-20;修回日期:2011-12-19
基金项目:国家自然科学基金资助项目(50975083);湖南省科技重大专项计划项目(2010FJ1003)
通信作者:刘士士(1986-),女,河南濮阳人,硕士研究生,从事整车性能分析与优化研究;电话:13508487734;E-mail: liushishi21@163.com