J. Cent. South Univ. Technol. (2011) 18: 889-897

DOI: 10.1007/s11771-011-0778-3

Application of 1D/3D finite elements coupling for structural nonlinear analysis

YUE Jian-guang(岳健广)^{1, 2}, A. Fafitis², QIAN Jiang(钱江)¹, LEI Tuo(雷拓)¹

1. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;

2. Department of Civil Engineering, Arizona State University, Tempe, AZ 85287, USA

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: An element coupling model (ECM) method was proposed to simulate the global behavior and local damage of a structure. In order to reflect the local damage and improve the computational efficiency, three-dimensional (3D) solid elements and one-dimensional (1D) beam element were coupled by the multi-point constraint equations. A reduced scale 1?8 model test was simulated by the ECM and a full three dimensional model (3DM) contrastively. The results show that the global behavior and local damages of ECM agree well with the test and 3DM. It is indicated that the proposed method can be used in the structural nonlinear analysis accurately and efficiently.

Key words: elements coupling model; global behavior; local damage; multi-point constraint equations; nonlinear analysis

1 Introduction

The length scale of structural engineering varies from local scale to global scale [1]. Normally, the local damages have great impact on the global behavior. In order to predict a structure behavior completely, it is necessary to appropriately capture the global behavior and the local damages at the same time.

In finite element methods (FEM), a fully three- dimensional numerical technique is a good tool to describe the mechanical details with high computational cost, and a fully one-dimensional numerical technique can well predict the global behavior of a structure with low computational cost [2]. Then, the combination of the 3D and 1D technique was used to describe the global/ local behavior in one structure, such as some proposed methods: the coupling of FEM/FEM and the transmit elements [3-7].

The kinematic coupling is widely used for the coupling of FEM/FEM to avoid the usage of the multi-point constraints or Lagrange multipliers, but it cannot predict the stress of the interface accurately [2]. Some researchers proposed the multi-point constrain equations coupling method which can be achieved by the energy conservation law on the interface between different elements [3-5]. This method has been shown to give good results for coupling beam-solid elements, beam-shell elements and shell-solid elements, while it needs to solve the stress of the interface based on the elastic mechanics theory, so it is mainly used for the linear calculations now.

Another strategy is to elaborate specific finite element to combine the different dimensional elements. KIM and HONG [6] presented three types of transition elements to solve the incompatibility related to different degrees of freedom between beam and wall element in FE analysis. Those transition elements show effective and reliable results in the analysis of the connections of coupled wall structures, and accuracy in modeling connecting beam. GARUSI and TRALLI [7] presented a new transition element for modeling solid-beam and plate-to-beam connections based on the hybrid stress method. The stress field solution of the de Saint Venant problem was assumed within the transition element.

In this work, the authors proposed an elements coupling model (ECM) combined with 1D/3D elements by the multi-point constraint equations to predict the nonlinear global/local behavior of a structure. This model is divided into linear regions and nonlinear regions, in which the local damages mainly occur in the nonlinear regions. The linear concrete model and the concrete plastic damage model are used to describe the concrete linear behavior and nonlinear behavior, respectively. A reinforced concrete pipe column test and a composite structure test were calculated by this method for verification, and a fully 3D elements model was used to verify this method as a powerful assistant tool.

2 ECM with 1D/3D elements

2.1 Coupling of 1D element with 3D elements

With ABAQUS software, one dimensional beam element and three dimensional solid elements can be coupled by the multi-point constraint equations. Those constraint equations can be written in a normal form:

                                  (1)

where u is the nodal freedom of the beam element, u′ is the nodal freedom of solid element, n is the number of solid elements on the interface (see Fig.1), and X_i is the constraint coefficients of node i.

Fig.1 Coupling of 1D element with 3D elements

According to the energy conservation, the work done by the nodal stress of solid elements on the interface should be equal to the work done by the nodal force of the beam element which is coupled with the solid elements on the interface. Under different nodal forces of 1D element, the energy conservation equations of the coupling can be written as

                            (2)

                            (3)

                           (4)

                            (5)

                            (6)

                    (7)

where A is the interface area, F_i is the nodal force acting on the 1D element along the axis i, σ_3i is the component of the stress on the interface along the axis i, u_i is the displacement component of the beam element node on the interface along the axis i, and  is the displacement component of the solid element node on the interface along the axis i.

Based on the theory of mechanics of materials, the stress on the interface can be obtained (for thin-walled circular section):

            (8)

            (9)

                        (10)

where x and y are the nodal coordinates of the solid elements on the interface, axis 1 is the x direction and axis 2 is the y direction, and the origin point of this coordinate system is located at the beam node on the interface; I₁ and I₂ are the principal moments of inertia of the interface with respect to the axis 1 and axis 2; A₀ is the area which is bounded by the middle line of the section wall; t is the thickness of the section wall; R₀ is the average radius of the section.

Substituting the equation of the nodal stress into the equation of the energy conservation of coupling, the multi-point constraint equations can be written as

     (11)

    (12)

             (13)

            (14)

            (15)

  (16)

where A_i is the element area on the interface, [N] is the shape function matrix of solid elements on the interface, [X] is the coefficient matrix of multi-point constraint equations, {u′}_i is the nodal freedom matrix of elements i on the interface, and [u′] is the nodal freedom matrix on the interface. Because the stress of the interface is obtained from the theory of mechanics of materials, the multi-point constraint equations are linear.

2.2 Concrete plastic damage model

In this work, the concrete plastic damage model of ABAQUS is used to describe the concrete nonlinear behavior. In the plastic-damage modal for concrete presented by LUBLINEAR et al [8], there is only one fracture-energy-based scalar damage variable used to represent all damage states. This model can simulate the monotonic loading but is not appropriate for the cyclic loading of concrete. LEE and FENVES [9] presented a nonlinear damage model for the cyclic loading, with two damage variables, one for the tensile damage and the other for the compressive damage, and a yield function with multiple-hardening variables. Its basic equation is

                   (17)

where  is the effective stress, and E₀ is the initial linear-stiffness tensor. The strain tensor ε is decomposed into the linear part ε^e and the nonlinear part ε^p. F is an isotropic, first-degree homogeneous scalar function with multiple-hardening evolution.

The nonlinear strain rate  is evaluated by a flow rule, which is assumed to be generated from a scalar nonlinear potential function

                             (18)

where  is a nonnegative function referred to as the nonlinear consistency parameter.

The damage variable κ is defined by κ_t and κ_c, which are independent state variables. The evolution is expressed as

                              (19)

where H is the function to give the expression of the damage date.

The total stress σ is determined by evaluating the degradation damage from

                             (20)

where the degradation damage variable D is defined as D=D(κ)=1-(1-D_t)(1-D_c), which describes the tensile D_t and the compressive D_c degradation damage responses. More details of the concrete nonlinear damage can be found in Ref.[9].

The model proposed by DESAYI and KRISHNAN

[10] is used for the uniaxial compressive stress-strain curve for concrete in this study:

                        (21)

where ε₀ is the strain corresponding to the peak stress,  E_c is the initial linear modulus of the concrete, and  is the concrete cylinder strength. Here, the limited compressive strain is assumed to be ε_u=  0.003 5.

By direct stress-crack strain curve, the concrete tensile stress-strain curve reflects the tensile softening and is assumed as linear before tensile peak stress. After the peak stress, the tensile stress-strain relationship is given as follows [11]:

               (22)

where f_t is the concrete tensile strength, ε_tu is the concrete limited tensile strain (here it is equal to 0.001), and c₁ and c₂ are equal to 9.0 and 5.0, respectively.

The compressive damage variable and tensile damage variable are written as

                  (23)

                  (24)

where  and  are the compressive and tensile plastic strains, b_c and b_t are equal to 0.7 and 0.1 [12], respectively.

2.3 ECM modeling strategy

Figure 2 shows the ECM modeling strategy of a cantilever column. Normally, the concrete damage mainly occurs in a local region such as the plastic hinge, and the rest region almost keeps linear behavior, therefore the member was divided into linear region and nonlinear region. In order to use the coupling of 1D/3D, the linear region was divided into two parts. In Part 1 (see Fig.2), 1D elements were used to simulate the concrete behavior with linear concrete model. In Part 2, 3D elements are used to describe the concrete behavior also with linear concrete model. In the nonlinear region, 3D elements with the concrete plastic damage model were used to describe the concrete nonlinear behavior.

Fig.2 ECM modeling strategy of cantilever column

The length of the nonlinear region, L_p, was assumed as

L_p=L₃=3L_h                                  (25)

where L_h is the length of the plastic hinge, L_h=0.5D, and D is the section diameter of the column [13].

The length of part 2 was assumed as

L₂=L_h                                      (26)

Figure 3 shows the ECM modeling strategy of a structure. The structure was also divided into linear and nonlinear region. The linear region was also divided into two parts. Part 1 was simulated by 1D element with linear concrete model, part 2 was simulated by 3D element with linear concrete model, and the nonlinear region was simulated by 3D element with nonlinear concrete model.

3 ECM verification of member

3.1 Linear numerical calculation

In order to verify the accuracy of the proposed multi- point constraint equations, a linear ECM was taken as an example. Figure 4 shows a cantilever column subjected to axial force F₃, shear force F₁, bending moment F₄ and torsion moment F₆. The material behavior is linear. The details of this example are shown in Fig.4. The calculated stress results of points A₁, A₂, A₃ and A₄ on the interface will be compared with the analytical solution.

Table 1 shows the stress comparison of the analysis results and numerical results. The agreement of the analytical and numerical results shows that the coupling method of multi-point constrain equations can predict the stress of the coupling interface accurately in linear behavior. The stress contours of the numerical results are shown in Fig.5.

3.2 Nonlinear numerical calculation

TU [14] and RONG [15] had done a quasi-static test of a reinforced concrete pipe column. The column test model details are shown in Fig.6. The compressive strength of the concrete was 42.0 kN/mm². A constant vertical load of 360 kN acted on the top of the column, and a horizontal slowly increasing load acted on the top of the column controlled by the top displacement. As the top displacement was increasing, cracks developed at the bottom of the column, and the concrete was mainly damaged at the bottom.

The column test was simulated by the 3DM and ECM. According to the ECM modeling strategy, the ECM of the column test was modeled as shown in Fig.6. In the two models, the steel of the longitudinal and hoop reinforcement was assumed to have elastic-plastic behavior, with yield strengths of 360 kN/mm² and   210 kN/mm², respectively. The concrete nonlinear behavior was described by the plastic damage model.

Fig.3 ECM modeling strategy of structure

Fig.4 Example details (Unit: mm)

Table 1 Comparison of analytical and numerical stress results

Fig.5 Numerical stress results under action of different parameters: (a) Axial force F₃; (b) Bending moment F₄; (c) Torsion moment F₆; (d) Shear force F₁

In the 3DM, the concrete of the whole column was assumed to have nonlinear behavior. The concrete and reinforcement of the column were simulated by the C3D8R elements and T3D2 elements, respectively. C3D8R is eight-node linear brick, reduced integration with hourglass control continuum element and T3D2 is 3D stress/displacement two-node linear displacement truss element. The reinforcement elements were embedded in the concrete elements.

Fig.6 Column test model details and its 3DM and ECM (Unit: mm)

In the ECM, the length of part 1 and part 2 are    2 070 mm and 250 mm, respectively. The concrete of part 1 and part 2 is assumed to have linear behavior. In part 1, the concrete is simulated by B31 elements. B31 is a Timoshenko two-node linear beam element in space. In part 2 and the nonlinear region, the concrete and reinforcement simulation are simulated by the C3D8R and T3D2 elements, respectively. The 1D and 3D elements are coupled by the multi-point constraint equations method.

Figure 7 shows the load-displacement curves of the test and two models. The calculated results are very similar to the results of the test in the linear stage. In the nonlinear stage, the test results is a little larger than the calculated ones. The limit load of the test is 67.4 kN [14-15], and the calculated limit load of 3DM and ECM are 61.7 kN and 60.8 kN, respectively. These results indicate that both models can reflect the column behavior well.

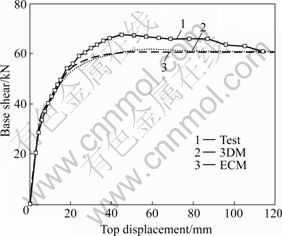
Fig.7 Comparison of load-displacement curves

The accuracy of ECM was verified by the 3DM with the comparison of the max equivalent plastic strains. The equivalent plastic strain gives a measure of the amount of permanent strain and it is calculated from the component plastic strain. Equivalent plastic strain is defined as  where  is the equivalent plastic strain rate. Figure 8 shows the relation of the column top displacements and concrete max equivalent plastic strain. The max equivalent plastic strain of 3DM and ECM are 0.013 and 0.012, respectively. Figure 9 shows the contours of concrete max equivalent plastic strain of the two models. In Fig.9, PEEQ denotes the equivalent plastic strain in the uniaxial compression, the “Avg:75%” denotes that the averaged threshold is 75%, which determines how element- and surface-based variables are calculated at the nodes.

Fig.8 Top displacement-equivalent nonlinear strain curves of two models

Those results shows that the 3DM can reflect the behavior of column completely, and the concrete damage mainly occurs at the bottom of the column. Although the ECM cannot describe the column behavior completely like 3DM, it captures the main local concrete damage at the same accuracy of 3DM.

4 ECM verification of structure

4.1 Test model

BAI et al [16] had conducted a pseudo static model test of a substructure from a direct air cooled condenser support platform. The real platform (see Fig.10) is a vertical hybrid structure consisting of reinforced concrete pipe columns and steel truss. The pipe column height is about 40 m, the section diameter is about 4 m and the thickness is about 0.5 m. The steel truss height is about  8 m. The total mass of the equipments on the platform is more than 10⁴ t.

Fig.9 Comparison of concrete max PEEQ of two models:    (a) 3DM; (b) ECM

The reduction scale of the test model (see Fig.11) is 1:8 for the overall dimensions of the structure as well as the dimensions of the members (columns and truss). Two hydraulic-servo actuators (see Fig.11) were used to apply the loads on the structure through the loading transfer device, which transferred the loads from the hydraulic-servo actuator to 14 loading points (see Figs.11 and 12) of the structure. The ratio of the loading points is shown in Fig.12. Displacement gauges (see Fig.12) were used to measure the structure top displacement, the truss displacement, the column top displacement and the column middle displacement. In the pseudo-static test, the test loading was controlled by the top displacement. More information can be found in Ref.[17].

Fig.10 Direct air cooled condenser support platform

4.2 Numerical models

The test model was simulated by the 3DM and ECM. The details are shown in Fig.12. The measured value of concrete compressive strength is 26.64 MPa, the strength grades of longitudinal reinforcement and hoop reinforcement are HRB400 (yield strength of 400 MPa) and HRB235 (yield strength of 235 MPa), respectively. The truss is made of square steel tubular members, its major sections are 60 mm×2.5 mm, 60 mm×2.0 mm,  50 mm×1.5 mm and 25 mm×1.5 mm, and its steel strength grade is Q235 (yield strength of 235 MPa).

In 3DM (see Fig.12), the material of the whole structure was assumed to have nonlinear behavior. The concrete and reinforcement of column were simulated by C3D8R and T3D2 elements, respectively. The reinforcement elements were embedded in the concrete elements. The truss was simulated by B31 elements. The concrete slab on the truss was simulated by S4R element. S4R is a four-node, quadrilateral, stress/displacement shell element with reduced integration and a large-strain formulation.

In ECM (see Fig.12), each column is divided into two regions according to the ECM strategy. The lengths of part 1, part 2 and nonlinear region are 3 688, 250 and 750 mm, respectively. The steel of the truss structure was assumed to have nonlinear behavior. The concretes of part 1 and part 2 and nonlinear region were simulated  by B31 element, C3D8R element and C3D8R element, respectively. The reinforcements of part 2 and nonlinear region were simulated by T3D2 element and were embedded in the concrete elements. The truss was simulated by B31 element. The 1D element was coupled with the 3D elements by the multi-point constraint equations method.

Fig.11 Test model (a) and loading transfer device (b)

Fig.12 Test model, 3DM and ECM (Unit: mm)

The concrete nonlinear behavior was simulated by the plastic damage model. The steel nonlinear behavior of the truss and reinforcement was simulated by the elasto-plastic model. The concrete cubic compressive strength is 26.64 MPa. The yield strengths of longitudinal reinforcement and hoop reinforcement are 360 MPa and 210 MPa, respectively. The truss steel field strength is 215 MPa.

4.3 Nonlinear numerical calculation

The CPU calculation times of 3DM and ECM were 2 940 s and 70 s, respectively. The computational efficiency of ECM was approximately forty times faster than 3DM.

Figure 13 shows the comparison of the load- displacement of test, 3DM and ECM. The peak load of the test is 126.85 kN [17], and the calculated peak loads of 3DM and ECM are 128 kN and 124.4 kN, respectively. In the linear stage, both the ECM and 3DM predict the behavior of the test well. After the peak base shear, the capacity of ECM reduces more quickly than 3DM. It induced that the concrete max equivalent plastic strain of column of 3DM is larger than that of ECM (see Fig.14). Figure 14 shows the relation of the structure top displacement and concrete max equivalent plastic strain of column Z-B4 of 3DM and ECM. The max equivalent plastic strain of column Z-B4 of 3DM and ECM are 0.012 and 0.022, respectively.

Figure 15 shows the contours of the maximum equivalent plastic strain of concrete of 3DM and ECM. It is shown that the main concrete damages of column of 3DM and ECM are similar. Although there are some differences of results between 3DM and ECM, these results also indicate that the ECM can reflect the global behavior of the structure test and capture the main concrete damage of column at the same time, with a superior computational efficiency.

Fig.13 Load-displacement curves of test, 3DM and ECM

Fig.14 Top displacement-equivalent plastic strain curves of test, 3DM and ECM

Fig.15 Concrete max equivalent plastic strains: (a) Results of 3DM; (b) Results of ECM

5 Conclusions

1) The 1D element can be coupled with 3D elements by the multi-point constraint equations. These linear equations were obtained from the energy conservation and the mechanics theory of materials. A linear calculation example verified the accuracy of these equations.

2) An ECM modeling strategy was proposed to be used for the structural nonlinear analysis. A member or a structure was divided into linear region and nonlinear region. The linear region was divided into two parts which were simulated by 1D elements and 3D elements, respectively. Then, the 1D element and 3D elements were coupled in the linear region.

3) A pipe column test and a structure static test were used to verify this ECM method. The results indicate that the ECM of a member or a structure can reflect the global behavior of a member or a structure, and capture the main local concrete damages of a member or a structure with a superior computational efficiency.

References

[1] LI Zhao-xia, ZHOU Tai-quan, CHAN T H T, YU Y. Multi-scale numerical analysis on dynamic response and local damage in long-span bridges [J]. Engineering Structures, 2007, 29(7): 1507-1524.

[2] MATA P, BARBAT A H, OLLER S. Two-scale approach for the nonlinear dynamic analysis of RC structures with local non-prismatic parts [J]. Engineering Structures, 2008, 30(12): 3667-3680.

[3] MCCUNE R W, ARMSTRONG C G, ROBINSON D J. Mixed-dimensional coupling in finite element models [J]. International Journal for Numerical Methods in Engineering, 2000, 49(6): 725-750.

[4] SHIM K W, MONAGHAN D J, ARMSTRONG C G. Mixed dimensional coupling in finite element stress analysis [J]. Engineering with Computers, 2002, 18(3): 241-252.

[5] MONAGHAN D J, LEE K Y, ARMSTRONG C G, OU H. Mixed dimensional finite element analysis of frame models [C]// 10th ISOP Conference. Seattle, 2000: 263-269.

[6] KIM H S, HONG S M. Formulation of transition-elements for the analysis of coupled wall structures [J]. Computers & Structures, 1995, 57(2): 333-344.

[7] GARUSI E, TRALLI A. A hybrid stress-assumed transition element for solid-to-beam and plate-to-beam connections [J]. Computers & Structures, 2002, 80(2): 105-115.

[8] LUBLINER J, OLIVER J, OLLER S, ONATE E. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.

[9] LEE J H, FENVES G L. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[10] DESAYI P, KRISHNAN S. Equation for the stress-strain curve of concrete [J]. Journal of the American Concrete Institute, 1964, 61: 345-350.

[11] CORNELISSEN H A W, REINHARDT H W. Uniaxial tensile fatigue failure of concrete under constant-amplitude and program loading [J]. Magazine of Concrete Research, 1984, 36(129): 216-226.

[12] BIRTEL V, MARK P. Parameterised finite element modeling of RC beam shear failure [C]// 2006 ABAQUS User's Conference. Taiwan, 2006: 95-108.

[13] PARK R, PAULAY T. Reinforced concrete structures [M]. New York: John Wiley & Sons; 1975: 769.

[14] TU Feng. Experimental study and nonlinear finite analysis on seismic behavior of reinforced concrete pipe columns with large size and thin wall [D]. Xi'an: Xi'an University of Architecture and Technology, Department of Civil Engineering, 2006. (in Chinese)

[15] RONG Zhe. An experimental research on seismic behavior of great size thin wall reinforced concrete columns [D]. Xi'an: Xi'an University of Architecture and Technology, Department of Civil Engineering, 2006. (in Chinese)

[16] BAI Guo-liang, ZHU Li-hua, ZHAO Chun-lian, LI Hong-xing, LI Xiao-wen. Model test on behavior of direct air cooled condenser support platform under load and earthquake action [J]. Journal of Building Structures, 2008, 29(5): 42-49. (in Chinese)

[17] LI Hong-xing. Study on the support system for air cooled condenser of big power plant [D]. Xi'an: Xi'an University of Architecture and Technology, Department of Civil Engineering, 2006. (in Chinese)

(Edited by PENG Chao-qun)

Foundation item: Project(2007CB714202) supported by the National Key Basic Research Program of China; Project(SLDRCE10-B-07) supported by the Ministry of Science and Technology of China

Received date: 2010-04-30; Accepted date: 2010-11-20

Corresponding author: YUE Jian-guang, PhD candidate; Tel: +86-13524272150; E-mail: 79jgyue@tongji.edu.cn