DOI: 10.11817/j.issn.1672-7207.2015.03.014

一种分数阶时滞过程的内模控制器设计方法

赵志诚，李明杰，张井岗

(太原科技大学 电子信息工程学院，山西 太原，030024)

摘要：针对分数阶时滞过程提出一种内模控制器设计方法。根据分数阶过程稳定的充分必要条件给出了时滞过程稳定的阶次范围，采用内模控制(IMC)原理设计一种分数阶IMC控制器，该控制器仅有1个可调参数，且能利用最大灵敏度指标(M_s)实现参数的解析整定，以保证系统的鲁棒性。仿真结果表明：分数阶IMC控制器设计方法简单，参数整定方便，而且可使系统具有良好的目标值跟踪特性、扰动抑制特性以及克服参数变化的鲁棒性。

关键词：分数阶时滞过程；稳定性；内模控制；最大灵敏度；鲁棒性

中图分类号：TP273              文献标志码：A         文章编号：1672-7207(2015)03-0864-06

Design method of internal model controller for fractional order process with time-delay

ZHAO Zhicheng, LI Mingjie, ZHANG Jinggang

(School of Electronic Information Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)

Abstract: An internal model controller design method was proposed for a class of fractional-order process with time-delay. At first, the process order range was given according to the necessary and sufficient conditions of the fractional process stability. And a fractional order controller was designed based on internal model control (IMC) principle. The proposed controller has only one adjustable parameter, which can be derived through the maximum sensitivity (M_s) index. Resultantly, the robustness of the system can be achieved. The simulation results show that the design stategy is easy to implement and controller parameter tunning is convenient. Furthermore, the controller achieves a better target tracking performance, together with effective disturbance rejection property and stronger robustness against the parameters variation.

Key words: fractional order process with time-delay; stability; internal model control; maximum sensitivity; robustness

很多实际系统的变化过程具有复杂的动态特性，用整数阶微分方程描述其数学模型往往会产生很大的误差，而用分数阶微分方程则可以更加精确地描述系统的动态响应，具有更强的灵活性^[1]，因此研究分数阶系统的控制器设计方法受到了控制界的关注。目前最具代表性的分数阶控制器主要有以下4种^[2]：TID控制器、PI^λD^μ控制器、CRONE控制器和超前滞后校正补偿器，其中Podlubny提出的分数阶PI^λD^μ控制器，比传统PID控制器增加了2个可调参数，因此具有更大的可调范围，能够得到更好的控制效果，同时具有更强的鲁棒性^[3]。分数阶PI^λD^μ控制器的参数整定方法主要有幅值裕量和相位裕量法^[4]、极点阶数搜索法^[5]、随机搜索方法^[6]和微粒群优化算法^[7]等，但这些方法在应用中存在着复杂的运算，另外，为了便于控制器的设计，常常需将复杂的分数阶模型进行降阶处理，而基于逼近模型设计的分数阶控制器，往往存在误差而影响系统的控制品质。内模控制(IMC)是一种基于过程数学模型进行控制器设计的新型控制策略，由于其设计简单，调整方便，跟踪和控制性能好，因此得到了广泛的应用。为了便于内模控制的实际应用，可将内模控制结构转换为常规反馈控制结构，进而得到IMC-PID控制器，IMC-PID控制器仅有1个可调参数，有效地降低了参数整定的复杂度。本文作者针对一种分数阶时滞过程，分析了其稳定性条件，在此基础上，基于内模控制原理设计了一种分数阶控制器，并依据最大灵敏度(M_s)性能指标实现了控制器参数的解析整定，克服了参数整定的盲目性，同时保证了系统的鲁棒性，仿真结果表明了所提方法的有效性。

1  分数阶微积分与时滞过程的稳定性分析

1.1  分数阶微积分

最常用的分数阶微积分定义有Riemann- Liouville (RL)定义、Grünwald-Letnikov (GL)定义和Caputo定义，其中Caputo分数阶微积分的定义为：若f(t)在[0, t]上连续可微，则其分数阶微分和积分可分别表示为

   (1)

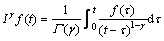         (2)

式中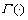：为Gamma函数，t＞0，分数阶阶次γ满足n-1＜γ＜n。Gamma函数的定义为

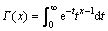，t＞0            (3)

式中：若x为正整数，则Γ(x)=(x-1)！。

假设f(t)的Laplace变换为F(s)，在零初始状态下，式(1)和(2)的Laplace变换分别为L{D^γf(t)}=s^γF(s)和L{I^γf(t)}=s^-γF(s)。

将传统整数阶PID控制器的微分项与积分项的阶次推广到分数域，得分数阶PI^λD^μ控制器输出u(t)的时域方程为

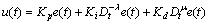     (4)

式中：λ和μ分别为积分和微分阶次，且λ, μ≥0，K_p，K_i和K_d分别为分数阶PI^λD^μ控制器的比例、积分和微分增益，e(t)为系统误差。

对式(4)进行Laplace变换得分数阶PI^λD^μ控制器的传递函数为

         (5)

当λ=μ=1时，G_c(s)为PID控制器；当λ=1，μ=0时，为PI控制器；当λ=0，μ=1时，为PD控制器；另外，若K_p=0，λ=1可得分数阶ID^μ控制器；若将PID控制器的比例环节用s^-1/n替换，可得TID控制器^[8]，其传递函数为

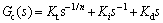        (6)

式中：n为非零正实数，K_t为可调参数。TID控制器可使闭环性能对参数变化不敏感，改善系统的鲁棒  性^[9]，若K_d=0，可得分数阶II^μ控制器，实质上是分数阶PI^λD^μ控制器的特殊形式。

1.2  分数阶时滞过程的稳定性分析

考虑分数阶模型特征多项式的一般形式

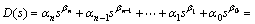
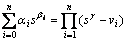           (7)

式中：α_i(i=0, 1, …, n)为任意常数，β_n, _.β_n-1, …, β₀为分数阶次，且有公共因子m(m∈R₊)，β_i=m·N，N为正整数，v_i为极点。分数阶过程稳定的充分必要条件为所有极点v_i都位于s平面的左半平面，或满足^[6]

|arg(v_i)|＞γπ/2                (8)

若令ω=s^m，将特征多项式映射到ω域，则分数阶过程稳定的充分必要条件为所有极点p_i满足^[10]

|arg(p_i)|＞mπ/2              (9)

考虑如下分数阶时滞过程：

           (10)

式中：K，T和τ分别为过程增益、时间常数和时滞时间，由其特征多项式D(s)=(Ts^γ+1)可知极点的最小相位为arg(v_i)=-π，由式(8)可知，当0＜γ＜2时，过程稳定；当γ=2时，过程临界稳定；当γ＞2时，过程不稳定。

为验证上述结论的正确性，当K=1，T=1.5，τ=0.5，γ分别取0.45，1.00，1.55，2.00和2.25时，过程的单位阶跃响应如图1所示。可见，γ＞2时，过程的响应发散而无法收敛于稳态值。另外，当γ=2.25时，过程模型经整数阶逼近后的极点在s平面上分布如图2所示，可见：右半s平面存在一对共轭复极点。同时，由γ=2.25=9/4可知：m=1/4，将过程模型改写成ω域中的表达形式，对应极点分布如图3所示，由式(9)可以判断ω右半平面极点p_1,2=0.898±0.327i为不稳定极点，因此γ＞2时分数阶时滞过程不稳定。

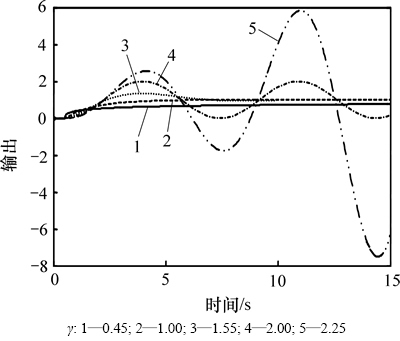
图1  不同γ时的阶跃响应

Fig. 1 Step response with different fractional orders

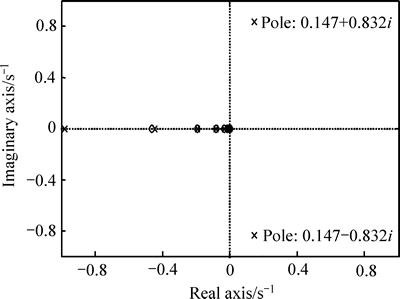
图2  γ=2.25时s平面零极点分布

Fig. 2  Zero-pole map in s plane when γ=2.25

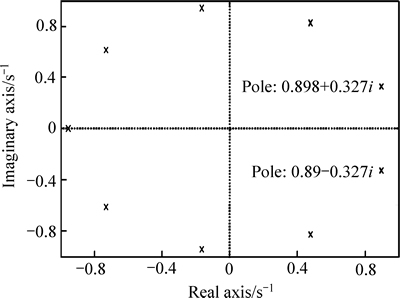
图3  γ=2.25时ω平面极点分布

Fig. 3  Pole map in ω plane when γ=2.25

2  分数阶时滞系统IMC控制器设计

内模控制系统结构如图4所示。其中：G_IMC为内模控制器，G_p为被控过程，G_m为过程模型，d为外部扰动，r和y分别为系统的输入和输出。图5所示为内模控制系统的等效反馈控制结构。其中G_c为反馈控制器。

图4  内模控制结构

Fig. 4  Structure of IMC

图5  内模控制等效反馈控制结构

Fig. 5  Equivalent feedback control structure of IMC

G_c和G_IMC有如下关系：

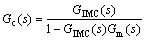          (11)

针对式(10)所示过程模型，选取低通滤波器f(s)=1/(hs+1)，h为滤波时间常数，根据内模控制原理可得内模控制器为

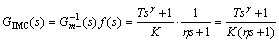      (12)

式中：G_m-为G_m的可逆部分。

将式(12)代入式(11)，并采用一阶泰勒级数逼近时滞环节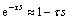可得等效反馈控制器G_c(s)为

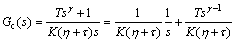     (13)

由式(13)可以看出：当0＜γ＜1时，G_c(s)为分数阶II^λ型控制器；γ=1时为常规PI控制器；1＜γ＜2时为分数阶ID^μ型控制器，参数η是分数阶控制器中唯一的可调参数，且与系统的动态响应性能、鲁棒性直接相关。

考虑到鲁棒性是控制系统的重要指标，文献[11]基于最大灵敏度，针对系统开环传递函数为一阶积分加时滞形式的系统，给出了内模控制器可调参数h与M_s之间的关系：

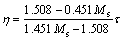            (14)

式中：M_s为最大灵敏度，其定义为

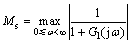           (15)

式中：G_l(jw)为系统开环传递函数的频率特性，M_s的取值范围一般为1.2~2.0，其值越小，系统的鲁棒性越好。

由式(10)和(13)得图5所示反馈控制系统的开环传递函数：

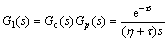        (16)

因此，可以利用式(14)实现控制器参数的鲁棒整定，克服了参数选择的盲目性。

3  仿真研究与分析

为了验证本文所提方法的有效性，将本文方法与文献[12-13]中的方法进行比较，并选择时间乘以误差绝对值积分(ε_ITAE)和超调量(σ)作为验证系统闭环性能的质量指标，较小ε_ITAE和σ意味着系统有较好的性能。

例1  考虑文献[12]中给出的分数阶时滞模型：

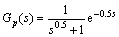          (17)

首先判定该过程是稳定的，利用本文方法设计内模控制器，由式(13)得IMC-II^λ控制器：

         (18)

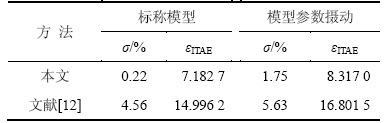
选择最大灵敏度指标M_s=1.45，由式(14)可得参数η的值，系统设定值输入为r(t)=1(t)，扰动输入为d(t)=-0.2(t-25)，得系统输出响应如图6所示。可见IMC-II^λ控制器能迅速实现对设定值的跟踪，同时对系统扰动有较好的抑制效果；文献[12]方法超调较大，动态响应较慢，闭环系统性能指标如表1所示，可见本文方法的ε_ITAE和σ性能指标均小于文献[12]方法的该性能指标。当系统时间常数和时滞时间均产生+10%的摄动时，系统的输出响应如图7所示，结合表1可见：本文方法具有更好的鲁棒性。

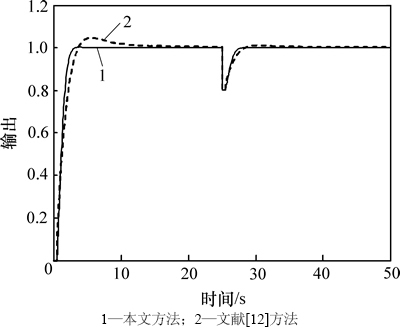
图6  控制系统阶跃响应曲线

Fig. 6  Step response curves of control system

图7  参数摄动时控制系统阶跃响应曲线

Fig. 7  Step response curves of control system with parameters perturbation

表1  控制系统性能参数

Table 1  Performance parameters of control system

例2  考虑文献[13]中的分数阶时滞模型：

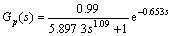         (19)

同样可知该过程稳定，用本文方法得IMC-ID^μ控制器：

      (20)

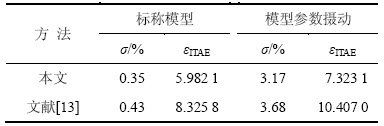
设系统的设定值输入为r(t)=1(t)；扰动输入为d(t)=-0.2(t-15)；文献[13]采用优化的方法整定控制器参数，本文方法选择最大灵敏度M_s=1.5整定控制器参数，系统输出响应曲线如图8所示。可见：IMC-ID^μ控制器响应较快，超调较小，具有较好的设定值跟踪和扰动抑制性能，系统性能指标如表2所示，可见：各指标均小于文献[13]方法。另外，在系统时间常数和时滞时间均产生+10%的摄动时，系统的输出响应如图9所示，结合表2可见较小的性能指标表明本文方法具有更好的鲁棒性。

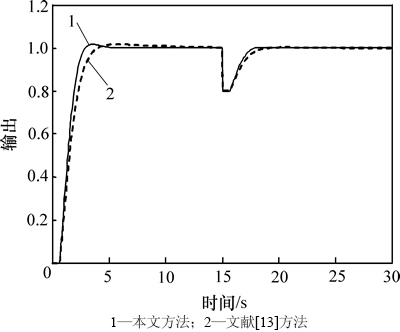
图8  控制系统阶跃响应曲线

Fig. 8  Step response curves of control system

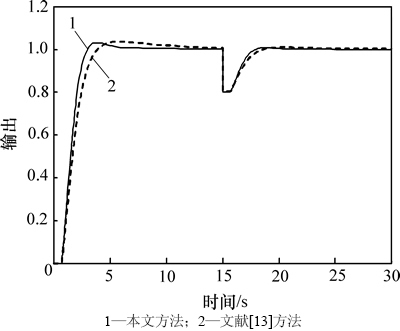
图9  参数摄动时控制系统阶跃响应曲线

Fig. 9  Step response curves of control system with parameters perturbation

表2  控制系统性能参数

Table 2  Performance parameters of control system

4  结论

1) 根据分数阶系统的稳定性条件，分析了时滞过程的稳定性，确定了保证过程稳定的分数阶次的范围(0＜γ＜2)。

2) 基于内模控制方法对分数阶时滞过程设计了分数阶内模控制器，并基于最大灵敏度M_s实现了控制器参数η的解析整定，克服了控制器参数的盲目选择，保证了闭环系统的鲁棒性。

3) 本文所提控制器设计方法不仅参数调整简单、方便，同时可以使系统具有较好的目标值跟踪特性、扰动抑制特性以及克服参数变化的鲁棒性。

参考文献：

[1] Mohammad S T. Notes on integral performance indices in fractional-order control systems[J]. Journal of Process Control, 2010, 20(3): 285-291.

[2] CHEN Yangquan, I, XUE Dingyu. Fractional order control-a tutorial[C]// 2009 American Control Conference. USA: IEEE, 2009: 1402-1416.

[3] 张博, 赵志诚, 王元元. 一种分数阶系统的内模控制器设计方法[J]. 太原科技大学学报, 2013, 34(2): 81-85.

ZHANG Bo, ZHAO Zhicheng, WANG Yuanyuan. A method of designing internal model controller for fractional-order system[J]. Journal of Taiyuan University of Science and Technology, 2013, 34(2): 81-85.

[4] 薛定宇, 赵春娜. 分数阶系统的分数阶PID控制器设计[J]. 控制理论与应用, 2007, 24(5): 771-776.

XUE Dingyu, ZHAO Chunna. Fractional order PID controller design for fractional order system[J]. Control Theory & Applications, 2007, 24(5): 771-776.

[5] 严慧, 于盛林, 李远禄. 分数阶PI^λD^μ控制器参数设计方法—极点阶数搜索法[J]. 信息与控制, 2007, 36(4): 445-450.

YAN Hui, YU Shenglin, LI Yuanlu. A design method of the parameters of fractional-order PI^λD^μ controller—Poles-orders searching method[J]. Information and Control, 2007, 36(4): 445-450.

[6] 李大字, 刘展, 靳其兵. 分数阶控制器参数整定策略研究[J]. 系统仿真学报, 2007, 19(19): 4402-4406.

LI Dazi, LIU Zhan, JIN Qibing. Study on optimization of fractional-order controller PID parameters[J]. Journal of System Simulation, 2007, 19(19): 4402-4406.

[7] CAO Junyi, CAO Binggang. Design of fractional order controller based on particle swarm optimization[J]. International Journal of Control, Automation and Systems, 2006, 4(6): 775-781.

[8] LUNE B J. Three-parameter tunable tilt-integral-derivate (TID) controller. US Patent US5371670[P]. 1994-12-06.

[9] 朱呈祥, 邹云. 分数阶控制研究综述[J]. 控制与决策, 2009, 24(2): 162-165.

ZHU Chengxiang, ZOU Yun. Summary of research on fractional-order control[J]. Control and Decision, 2009, 24(2): 162-165.

[10] 王振滨, 曹广益, 朱新坚. 分数阶线性定常系统的稳定性及其判据[J]. 控制理论与应用, 2004, 21(6): 922-926.

WANG Zhenbin, CAO Guangyi, ZHU Xinjian. Stability conditions and criteria for fractional order linear time-invariant systems[J]. Control Theory & Applications, 2004, 21(6): 922-926.

[11] ZHAO Zhicheng, LIU Zhiyuan, ZHANG Jinggang. IMC-PID tuning method based on sensitivity specification for process with time-delay[J]. Journal of Central South of Technology, 2011, 18(4): 1153-1160.

[12] D, COSTA J S. Tuning of fractional PID controllers with Ziegler-Nichols-type rules[J]. Signal Processing, 2006, 86(10): 2771-2784.

[13] LI Dazi, FAN Weiguang, JIN Qibing. An IMC-PI^λD^μ controller design for fractional calculus system[C]// Proceedings of the 29th Chinese Control Conference, Beijing: Beihang University Press, 2010: 3581-3586.

(编辑  陈爱华)

收稿日期：2014-05-05；修回日期：2014-07-22

基金项目(Foundation item)：国家自然科学基金资助项目(61203049)；山西省自然科学基金资助项目(2012011027-4) (Project (61203049) supported by the National Natural Science Foundation of China;Project (2012011027-4) supported by the Shanxi Natural Science Foundation of China)

通信作者：赵志诚，博士研究生，教授，从事先进控制技术研究；E-mail: zhzhich@126.com