GPS变形监测信号提取在矿山测量中的应用
来源期刊:中国有色金属学报(英文版)2014年第12期
论文作者:高井祥 胡 洪 刘 飞 李增科 姚一飞
文章页码:3949 - 3954
关键词:变形监测;GPS;卡尔曼滤波;EMD;噪声提取
Key words:deformation monitoring; GPS; Kalman filter; EMD; noise extraction
摘 要:介绍基本的GPS变形监测信号模型,并探讨GPS在矿区变形监测中存在的主要问题。针对GPS变形监测噪声信号提取问题,提出Kalman-EMD方法获取有效变形信息,并通过模拟和内蒙古伊泰矿区实际观测数据对该算法的有效性和准确性进行了验证。实验结果表明:利用该算法,GPS变形监测结果可以达到水准仪监测水平。
Abstract: The basic signal model of deformation monitoring with GPS was introduced and the main problems of GPS deformation monitoring in mining area were discussed. For the problem of noise signal extraction in GPS deformation monitoring, the Kalman-EMD method was proposed to obtain the effective deformation signal. The reliability and effectiveness of the methodology were tested and verified by analog signal. The results of experiment in Mongolia show that the accuracy of the proposed GPS deformation monitoring model is equivalent to that of level method.
Trans. Nonferrous Met. Soc. China 24(2014) 3949-3954
Jing-xiang GAO1, Hong HU1,2, Fei LIU1,2, Zeng-ke LI1,2, Yi-fei YAO1,2
1. Key Laboratory for Land Environment and Disaster Monitoring of SBSM, China University of Mining and Technology, Xuzhou 221116, China;
2. School of Environment and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
Received 10 July 2013; accepted 26 February 2014
Abstract: The basic signal model of deformation monitoring with GPS was introduced and the main problems of GPS deformation monitoring in mining area were discussed. For the problem of noise signal extraction in GPS deformation monitoring, the Kalman-EMD method was proposed to obtain the effective deformation signal. The reliability and effectiveness of the methodology were tested and verified by analog signal. The results of experiment in Mongolia show that the accuracy of the proposed GPS deformation monitoring model is equivalent to that of level method.
Key words: deformation monitoring; GPS; Kalman filter; EMD; noise extraction
1 Introduction
The traditional way of deformation monitoring in mining area is to utilize the level, theodolite and total station. With survey instruments and theory developing, the application of GPS in mining deformation monitoring becomes reality [1-5], such as GPS-RTK, and precise point positioning technology. For the signal of GPS monitoring contains both useful and noise parts, pre-data processing is a necessary step to get rid of noise to obtain useful information for further research of deformation monitoring, and the main methodologies are polynomial fitting and filtering method.
Noise, which exists around us, is unavoidable and interfering useful signals. Generally, noise can be divided into surveying noise and kinetics noise. Surveying noise which is independent of kinetics system, is caused by surveying instruments and digital translation processing. For example, in GPS short baseline, multipath effect cannot be eliminated by double difference. It becomes a main obstacle in GPS high precision surveying and affects judgment of tendency of control points. The deformation information in short period is usually hard to distinguish from noise for similar characteristics. Kalman filter has unique advantages in term of removing white noise and predicting the future state of the system [6,7], while EMD is good at information extraction ability [8]. In this work, the method of extracting deformation information was investigated based on Kalman noise filtering capabilities, and the deformation information extraction was focused based on Kalman-EMD model. Finally, taking the dynamic GPS data of mining area of Inner Mongolia Yitai Group Suancigou surface coal mining area as an example, the law of surface subsidence was evaluated by Kalman- EMD model.
2 Dynamic deformation signal
Noise is composed of plus noise and square noise due to different ways of collection. So, monitoring signal cannot be described precisely. Plus noise is irrelevant dimension of signal. Deformation signal can be depicted as
f(t)=s(t)+n(t) (1)
where s(t) is deformation information and n(t) is noise. It can be seen that signal value is determined by its statistical characteristics and can not be polluted by noise signal. In most cases, noise signal value does not change too much.
is determined by its statistical characteristics and can not be polluted by noise signal. In most cases, noise signal value does not change too much.
3 Deformation signal extraction based on Kalman-EMD
3.1 Kalman filter
The Kalman filter is a set of mathematical equations that provide an efficient computational (recursive) solution of the least-squares method. The filter is very powerful in several aspects [9,10]: It supports estimations of past, present, and even future states, though the precise nature of the modeled system is unknown [11,12]. To extract white noise, we need to establish state equations and observation equations. After discretization, the mathematical model of Kalman filter can be defined as
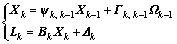 (2)
(2)
where Xk is the state vector at epoch k; Lk is system measurement vector at epoch k; ψk,k-1 is the state transition matrix from epoch k-1 to k;  is the system noise matrix; the term Ωk-1 is the process driving noise at epoch k-1; Bk is the system measurement matrix at epoch k; Δk is the measurement noise at epoch k.
is the system noise matrix; the term Ωk-1 is the process driving noise at epoch k-1; Bk is the system measurement matrix at epoch k; Δk is the measurement noise at epoch k.
When standard Kalman filter is adopted to deal with deformation signal, the filtering equation is
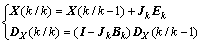 (3)
(3)
where

where X(k/k-1) is forecast value; DX(k/k-1) is its covariance matrix; Jk means state gain matrix; Ek represents predictive residuals.
Kalman filter is a series of the recursive calculative formulas [13], which means that prediction and modification happen constantly in the progress. It does not need a large number of observation data in state estimation, and when new observation data are available, filtered value of state can be obtained at anytime so that we can get real-time observation results [14].
3.2 EMD
EMD is a signal analysis method proposed by HUANG of NASA, which conducts signal decomposition based on its time scale characteristics without setting any basis functions before. Theoretically, EMD can be applied to any kind of signal decomposition [15]. Especially, when dealing with non-stationary or non-linear data, EMD is more appropriate [16]. No matter how complicated the signal is, it can be treated as different simple and non-sinusoidal components. Different from other filter decomposition techniques, EMD introduces distance of maxima and minima to determine local scale, making decomposition self adaptive and fully data-driven [17]. Experience shows that the progress of decomposition conforms physical laws and can extract the basic approximate signal cycle. Decomposed IMF meets instantaneous frequency characteristics, which facilitates monitoring of the signal transient characteristics and long-term trend extraction. It has been verified that the precision of deformation information extraction is higher than that of direct extraction because EMD is influenced by the cumulative impact of noise at each decomposition scale [18].
The operators calculated IMF from EMD and residual are defined as  and
and 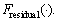 And the above two operators also define the similar processing of high frequency and low frequency filtering. The decomposition formula from scale i to i+1 is designed as follows:
And the above two operators also define the similar processing of high frequency and low frequency filtering. The decomposition formula from scale i to i+1 is designed as follows:
fi+1(t)=Fimf(ri(t)) (4)
ri+1(t)=Fresidual(ri(t)) (5)
The reconstruction equation is
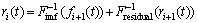 (6)
(6)
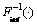 and
and  are inverse processes of Fimf(.) and Fresidual(.).
are inverse processes of Fimf(.) and Fresidual(.).
The original signal can be expressed as follows:
 (7)
(7)
3.3 Deformation signal extraction with Kalman-EMD
Related works have confirmed that Kalman filter can effectively remove white noise in the signal. In this work, the model of deformation information extraction using EMD based on Kalman filter is proposed. It takes advantage of Kalman filter to get rid of noise prior to using EMD to obtain high accuracy deformation information. Figure 1 illustrates the basic idea of the deformation information extraction model.

Fig. 1 Flow chart of Kalman-EMD model for mining deformation with GPS
4 Validation
From Eq. (1), we assume that the data collection model is
ui=yi+et (8)
where et is normal white noise sequence and yt is signal value of ut.
Analog noise signal is
yt=sin(2πt/150)
Sampling interval Δt=1 s and sample size is 1690. The signal mixed with Gaussian white noise which conforms to normal distribution is shown in Fig. 2, while Fig. 3 shows that processed after Kalman filter.
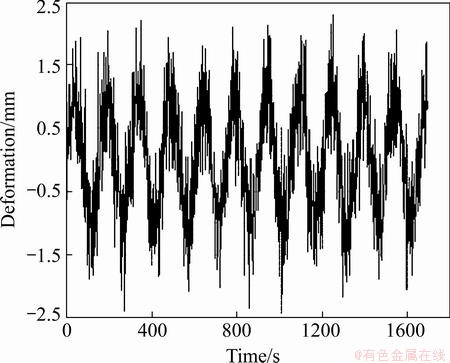
Fig. 2 Original analog signal with useful signal and noise
The original signal extracted by EMD is shown in Fig. 4 and Fig. 5 depicts that dealt after Kalman filter. Because the quality of original signal is not very good, Fig. 4 does not show components of IMF (1). Compared with Fig. 5, it can be found that the original clean components IMF (5) extracted by means of EMD form

Fig. 3 Signal after noise reduction by Kalman filter

Fig. 4 Multi-scale decomposition of original signal
original signal added with noise have generated obvious deformation. In contrast, noise reduction dealt after Kalman filter possesses clear complete cycle characteristics, consistent with the original signal yt=sin(2πt/150), confirming that the assumption above is correct. The evaluation indexes are given in Table 1, from which we can see that Kalman-EMD has evident effect on signal extraction.

Fig. 5 Multi-scale decomposition of signal after Kalman filter
Table 1 Evaluation of noise reduction with Kalman

5 Case study
The experiment was conducted on a mine of Inner Mongolia Yitai Group, located in Ordos Loess Plateau, covered with thick loess and aeolian sand. In this area, vegetation is sparse, and settlements are scattered. Moreover, as affected by water erosion, ground fluctuates considerably and the relative elevation difference is 50 m, belonging to typical Hilly areas. Deformation monitoring, especially dynamic deformation monitoring can be hardly carried out by traditional leveling method. What’s more, the regularity of surface movement and surface movement parameters are different. All these reasons together bring it difficult to select parameters of surface mobility prediction and protectoral coal pillar design. In order to get more accurate and detailed access to real-time dynamic deformation data the surface of, we conducted dynamic monitoring experiments at typical subsidence monitoring points by means of GPS (RTK mode). The experiment was combined with level, theodolite and total station to validate the feasibility of usage of GPS for continuous dynamic deformation monitoring. The experimental apparatus Huace X90 series receiver worked 30 h from 8:00 am on December 3, 2008 to 6:00 pm on December 4, 2008 at sampling interval of 5 s with satellite cut-off elevation angle of 10°. Total station was used to monitor the points every 1 min and level was used to check stability every 4 h. Considering that subsidence is the main surface movement, the experiment took H directional signal analysis.
Multi-scale decomposition of the original signal extracted by EMD is shown in Fig. 6 and Fig. 7 depicts that dealt after Kalman filter. We can see from Fig. 6 and Fig. 7 that using only the EMD method for separating the IMF still obtains localized distortion components. By comparing Kalman-EMD model with the EMD-only method, the quality of noise-canceling is decomposing significantly improved.
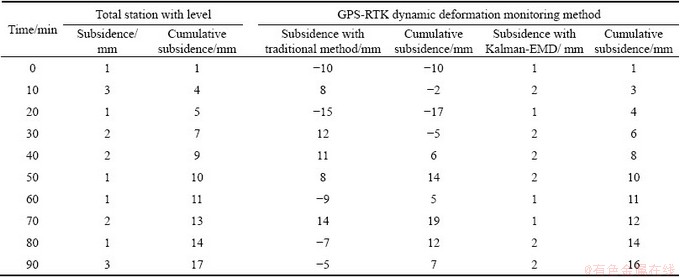
We regard the traditional method as “true” value, because it could reflect the real land deformation. From Table 2, the subsidence of GPS-RTK raw data every 10 min is about ±10 mm, while the actual subsidence is only less than ±3 mm, and the maximum error of monitoring is 17 mm, much lager than the tolerance requirements. The difference between cumulative subsidence and the actual subsidence has reached 10 mm. which has lost significance. And this is the reason why GPS was not be used in deformation monitoring. However, with Kalman-EMD model, the subsidence is nearly the same with the traditional method, subsidence monitoring is consistent with the actual amount of subsidence, and the maximum error is less than ±1 mm. The results show that the accuracy of Kalman-EMD model is much higher than the required accuracy specifications, thus confirming the model presented in this section has good practical engineering significance.

Fig. 6 Multi-scale decomposition with EMD only

Fig. 7 Multi-scale decomposition with EMD after Kalman filter
Table 2 Comparison of subsidence of surface points in 90 min
6 Conclusions
1) The composition is analyzed based on Kalman filter and EMD and the model of Kalman-EMD is proposed to extract GPS deformation information. The reliability of this method is verified by analog signal analysis.
2) The proposed model can effectively extract deformation information and its precision can reach a comparable level of leveling.
3) Kalman-EMD model of GPS deformation monitoring data processing can effectively improve the accuracy of GPS dynamic continuous monitoring and subsidence monitoring is consistent with the actual subsidence, which is confirmed by experiment conducted at Inner Mongolia Yitai Group.
References
[1] HAN Bao-ming, OU Ji-kun, CHAI Yan-ju, LU Xiu-shan. Method for processing data observed from GPS for subsidence surveying in mining area [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(5): 1035-1039. (in Chinese)
[2] GAO Jing-xiang, LIU Chao, WANG Jian, LI Zeng-ke, MENG Xiang-chao. A new method for mining deformation monitoring with GPS-RTK [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(s3): 659-664.
[3] XU Chang-hui, WANG Jin-ling, GAO Jing-xiang, WANG Jian, HU Hong. Precise point positioning and its application in mining deformation monitoring [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(s3): 499-505.
[4] SHAN Zheng-ying, HAN Hou-zeng, JIANG Kun. Optimization model of GNSS/pseudolites structure design for open-pit mine positioning [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(7): 2201-2208.
[5] LIU Guo-lin, ZHANG Lian-peng, OU Ji-kun. Method of multi-level recursive and application to nonlinear dynamic deformation forecasting [J]. Transactions of Nonferrous Metals Society of China, 2005, 15(1): 164-167.
[6] TSAKALOZOS N, DRAKAKIS K, RICKARD S. A formal study of the nonlinearity and consistency of the empirical mode decomposition [J]. Signal Processing, 2012, 92(9): 1961-1969.
[7] XIAO Jie, ZHANG Jin. Analysis and application of automatic deformation monitoring data for buildings and structures of mining area [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(s3): 516-522.
[8] TANG Bao-ping, DONG Shao-jiang, TAO Song. Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation [J]. Signal Processing, 2012, 92(1): 248-258.
[9] HAUSCHILD A, MONTENBRUCK O. Kalman-filter-based GPS clock estimation for near real-time positioning [J]. GPS Solutions, 2009, 13(3): 173-182.
[10] ZHOU Ze-bo, SHEN Yun-zhong, LI Bo-feng. A windowing- recursive approach for GPS real-time kinematic positioning [J]. GPS Solutions, 2010, 14(4): 365-373.
[11] YANG Yuan-xi, HE Hai-bo, XU Guo-chang. Adaptively robust filtering for kinematic geodetic positioning [J]. Journal of Geodesy, 2001, 75(2-3): 109-116.
[12] PETOVELLO M G, O’KEEFE K, LACHAPELLE G, CANNON M E. Consideration of time-correlated errors in a Kalman filter applicable to GNSS [J]. Journal of Geodesy, 2009, 83(1): 51-56.
[13] YANG Yuan-xi, GAO Wei-guang, ZHANG Xiao-dong. Robust Kalman filtering with constraints: A case study for integrated navigation [J]. Journal of Geodesy, 2010, 84(6): 373-381.
[14] HAN Song-lai, WANG Jin-ling. Integrated GPS/INS navigation system with dual-rate Kalman filter [J]. GPS Solutions, 2012, 16(3): 389-404.
[15] ANTONINO-DAVIU J A, RIERA-GUASP M, PONS-LLINARES J, ROGER-FOLCH J, PEREZ R B, CHARLTON-PEREZ C. Toward condition monitoring of damper windings in synchronous motors via EMD analysis [J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 432-439.
[16] BRAUN S, FELDMAN M. Decomposition of non-stationary signals into varying time scales: Some aspects of the EMD and HVD methods [J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2608-2630.
[17] OBERLIN T, MEIGNEN S, PERRIER V. An alternative formulation for the empirical mode decomposition [J]. Signal Processing, IEEE Transactions on, 2012, 60(5): 2236-2246.
[18] WANG Jian, WANG Jin-ling, ROBERTS C. Reducing GPS carrier phase errors with EMD-wavelet for precise static positioning [J]. Survey Review, 2009, 41(312): 152-161.
高井祥1, 胡 洪1,2, 刘 飞1,2, 李增科1,2, 姚一飞1,2
1. 中国矿业大学 国土环境与灾害监测国家测绘局重点实验室,徐州 221116;
2. 中国矿业大学 环境与测绘学院,徐州 221116
摘 要:介绍基本的GPS变形监测信号模型,并探讨GPS在矿区变形监测中存在的主要问题。针对GPS变形监测噪声信号提取问题,提出Kalman-EMD方法获取有效变形信息,并通过模拟和内蒙古伊泰矿区实际观测数据对该算法的有效性和准确性进行了验证。实验结果表明:利用该算法,GPS变形监测结果可以达到水准仪监测水平。
关键词:变形监测;GPS;卡尔曼滤波;EMD;噪声提取
(Edited by Yun-bin HE)
Foundation item: Project (2014ZDPY29) supported by the Fundamental Research Funds for Central Universities, China; Project (CXZZ11-0299) supported by the Postgraduate Innovative Program of Jiangsu Province, China
Corresponding author: Jing-xiang GAO; Tel: +86-516-83590159; E-mail: jxgao@cumt.edu.cn
DOI: 10.1016/S1003-6326(14)63555-X

