­­ Easy calibration method of vision system for in-situ measurement of strain of thin films

Jun-Hyub PARK¹, Dong-Joong KANG², Myung-Soo SHIN¹, Sung-Jo LIM²,

Son-Cheol YU², Kwang-Soo LEE³, Jong-Eun HA⁴, Sung-Hoon CHOA⁵

1. Department of Mechatronics Engineering, Tongmyong University, Busan, Korea;

2. School of Mechanical Engineering, Pusan National University, Busan, Korea;

3. Department of Automotive Engineering, Hoseo University, Chungcheongnam-do, Korea;

4. Department of Automotive Engineering, Seoul National University of Technology, Seoul, Korea;

5. Department of Nano/IT Engineering, Seoul National University of Technology, Seoul, Korea

Received 2 March 2009; accepted 30 May 2009

Abstract: An easy calibration method was presented for in-situ measurement of displacement in the order of nanometer during micro-tensile test for thin films by using CCD camera as a sensing device. The calibration of the sensing camera in the system is a central element part to measure displacement in the order of nanometer using images taken with the camera. This was accomplished by modeling the optical projection through the camera lens and relative locations between the object and camera in 3D space. A set of known 3D points on a plane where the film is located on is projected to an image plane as input data. These points, known as a calibration points, are then used to estimate the projection parameters of the camera. In the measurement system of the micro-scale by CCD camera, the calibration data acquisition and one-to-one matching steps between the image and 3D planes need precise data extraction procedures and repetitive user’s operation to calibrate the measuring devices. The lack of the robust image feature extraction and easy matching prevent the practical use of these methods. A data selection method was proposed to overcome these limitations and offer an easy and convenient calibration of a vision system that has the CCD camera and the 3D reference plane with calibration marks of circular type on the surface of the plane. The method minimizes the user’s intervention such as the fine tuning of illumination system and provides an efficient calibration method of the vision system for in-situ axial displacement measurement of the micro-tensile materials.

Key words: thin film; automatic camera calibration; adaptive binarization; plane homography; mechanical properties; strain measurement

1 Introduction

It is necessary that the mechanical properties of thin films are obtained to design an microelectromechanical system (MEMS) devices where they are used as structural materials and electrical materials. The size of the components used in MEMS device is usually in the order of micrometers. The mechanical properties of thin films show different characteristics from bulk materials. This is due to the fact that those properties are dependent on the dimensions and fabrication process of the material [1-4].

Many approaches[5-9] such as bend, bulge, resonance, nanoindentation, and tension have been presented for mechanical testing of microspecimens. However, these methods have some limitations. In bending-mode test, it is difficult to apply a large strain on a thin-film of a ductile material and a stress gradient occurs, causing non-uniform stress distribution across cross section. A bulge test can also could raise a stress concentration.

The direct tensile test would be the most favorable way to measure the tensile and fatigue properties. Especially, it is necessary to concurrently measure the load and displacement when tensile test for a thin-film is performed to evaluate the mechanical properties. Using the overall displacements between the grips on specimen requires additional step of analysis by computing that can cause large errors and variations after yield of material.

Therefore, it is necessary to only measure strain corresponding to gage section of the tensile specimen. For this purpose, many approaches such as in-plane interferometry[10], AFM imaging[11], digital image correlation[12], out-of-plane interferometry[13] and digital image processing[14-17] are presented.

Also, many researchers have investigated in-situ displacement methods during micro-tensile test of thin films such as Moiré method, electronic speckle pattern interference method (ESPI) and correlation method. The Moiré method requires pre-process such as scale markers on very thin film, and ESPI method needs a rough surface of film to make speckle but films made by MEMS process have very smooth surface. And the Moiré method and electronic speckle pattern interference method (ESPI) are more expensive than using CCD.

OGAWA et al[16] presented a method for testing the mechanical properties of titanium thin films through image processing using two gauge markers of chromium oxide thin films that was deposited onto test films. SHARPE et al[14] measured the strain of silicon dioxide micro-specimens using digital image processing of two gold markers through illumination at a very oblique angle. MAZZA et al[15] showed that it was possible to measure the deformation of a micro-sample with nanometer resolution through image processing of least square template matching. It inherently requires image with enough textures so that there could be a restriction about specimens. The proposed method by the authors[17] needs the specimen with 8 indicators that is fabricated with the process and material the same as a real MEMS device. Another method by the authors[17] calculated the strain using number of pixels instead of displacement in the order of micrometer.

This paper describes an autonomous calibration method of a system using CCD camera for measuring the displacement in the order of nanometer during the micro-tensile test of thin films by observing the pixel displacement. For the camera calibration from a known standard scale and their projected image, some digital image processing methods such as adaptive binarization and plane homography were used as central element of the measurement system. To verify the performance of the proposed method, the tensile tests were performed using beryllium-nickel (BeNi) thin film that is widely used as a material in the structure of probe tips.

2 System configuration

To investigate a behavior of a material, the accurate relationship between the engineering stress and strain must be acquired. As can be seen in Fig.1, the configuration of system used in Ref.[17] was utilized in this study. The test system is also equipped with the deflectometer(capacitance type sensor) for measuring the displacement between the grips, load-cell for measuring the load and CCD camera system for measuring the extension of specimen. The measurement of extension of gage length is necessary to calculate the engineering strain. The measurement of the displacement between the grips can’t describe the accurate plastic behavior of material during the tensile test, as described in Ref.[17].

Fig.1 Schematic view of configuration of proposed system

The specimen was designed based on ASTM E466- 96 but all dimensions of the specimen could not be in compliance with the standard such as ASTM because of thin film[17]. The specimen was 1 000 μm width of reduced section and 30 μm thickness. The length of the reduced section is 6 000 μm and the radius of the blending fillet is 4 000 μm to minimize a stress concentration of the specimen. The smooth specimen was fabricated by wire-cut electric discharge method as shown in Fig.2(a). For the digital image processing based approach using CCD in this study, the eight black dots were marked on the surface of specimen at intervals of 1 mm using black pen and the aluminum plates about 2 mm thick were attached on grip ends using quick-drying glue for mounting specimen on the tester as shown in Fig.2(b). The specimen was mounted on tester using 4 bolts and 2 pins for tensile or high cycle fatigue test.

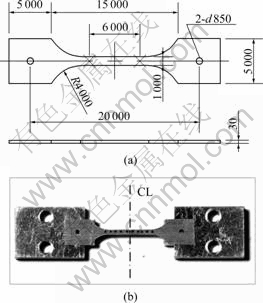
Fig.2 Structure of specimen: (a) Sketch of copper thin film specimen (t=30 μm); (b) Photo of specimen glued onto Al plates

3 Digital image processing

In the strain measurement system using CCD camera, the first step for the camera installation and calibration is to detect the image points of the calibration patterns marked on the calibration plate. One-to-one correspondence information between the pattern points on the calibration plate and their image projection should then be employed in the calibration algorithm with the coordinate data of the calibration points. Because the illumination conditions are always affected by the experimental environment, the extraction of calibration points is not consistent, and hence the decision of point coordinates and the correspondence under the existence of noisy data is a very difficult and inconvenient procedure in digital imaging measurement systems. Fig.3 shows the calibration target plate on which the small black circles are marked and the plate size is 14 mm×14 mm.

Fig.3 Example of calibration target plate with points of known dimension (mm)

The extraction of calibration points is typically performed with an image labeling algorithm after binarization of the gray-scale input image. Each blob region from image labeling includes the coordinate information of the calibration points. Because the calibration points and the background region of the calibration pattern image have unique intensity values, the simplest method to segment the point regions is image binarization.

Several binarization algorithms have been developed in the fields of machine vision[18]. Comparative evaluations of several methods and surveys of existing techniques can be found in Refs.[18-19].

Fig.4 presents the results of two representative binarization algorithms. Fig.4(b) presents the result of the Otzu method[20], a global thresholding algorithm, for the original images of Figs.4(a) and (c) give the result of Niblack’s method, a local adaptive thresholding algorithm[21]. Because the global binarization algorithm uses only one threshold value, a good binary image cannot be obtained when there is non-linear intensity variation in the image region due to light reflection, specifically as shown on the right side of Fig.4(b).

Fig.4 Comparison of two conventional binarization methods:  (a) Original gray-scale image; (b) Global image of binarization by single threshold value; (c) Local adaptive binarization method

The concept underlying the local adaptive method is to vary the threshold value for binarization over the image. The selection of the threshold value depends on the sample mean and standard deviation values in the local neighborhood of a specific location on the image.

Following the image binarization, an image labeling algorithm such as blob coloring[22] gives the coordinate information as the center position of each blob. The computing time of threshold value T in local adaptive binarization method is dependent on the size of the local window, in which the mean and variance should be calculated. For large window size, the computing time of T is very large. The image summing method such as integral image[23] can be used to speed-up the computation of the window values.

This paper uses the perspective transformation of a plane to extract point coordinates for calibration. A simple perspective projection is plane-to-plane mapping,which does not include lens distortion. If we have corresponding information of the coordinate values between the calibration patterns and their image points, then lens distortion parameters can be solved by a calibration algorithm. As four calibration points can create a projection matrix of a plane, plane-to-plane mapping can be applied to predict the input points of the calibration [24].

                 (1)

Eq.(1) shows the relationship between world coordinates x′ of 3D points on a calibration pattern plane and calibration coordinates x on an image plane transformed by a homography matrix H[25]. The value s is a scale factor and h₃₃=1 represents a constraint to limit the magnitude of the homography matrix elements.  Eq.(1) can be modified as

              (2)

    (3)

Using the pseudo-inverse formula of Eq.(3), if more than four points exist, it is possible to determine h₁₁-h₃₂ for the plane projection transformation.

Once the homography matrix is determined, the world coordinates of the points on the calibration plane can be transformed onto the image plane. Points with small distance errors between the pattern points and their projections on the image plane can then be used for solving the calibration parameters.

The parameter values of the homography matrix can be determined by a four-point correspondence between the calibration pattern points and their image projection. If there are other points except for the four points, we can verify the correspondence of the other points through plane-to-plane transformation by the H matrix solved by these four points.

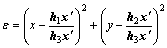                  (4)

Assume that we have two five-point groups, where one group is on a calibration target plane and another group is on their image plane by projection. We can then use the four points among each point set to calculate the homography matrix and one remaining point of each group is used to check the exactness of the calculated homography matrix. If there is large distance error between one point on the plane and its projected coordinate on the image plane, the plane homography correspondence between the two groups is not exact and the point set should be discarded.

The cross-type pattern of the five points is a projection of a set of a small number of points on the calibration pattern plane. The origin of the coordinate system can be assumed to always be located at the center point of the set. The four outer reference points of the cross pattern are at the same distances from the center point of the cross pattern. In the five point group, four points have a symmetric form with respect to the center point of the set, and the correspondence problem between the image points and reference points on the calibration pattern can be solved simply by extracting the equivalent pattern for blob points on the image plane.

Although the projected circle center differs from the ellipse centers, as noted in Ref.[26], the calibration pattern in this paper is a circle of a small size. This shape retains a fairly circular form even under severe perspective projection. As the direction of the camera axis for length measurement systems is typically similar to the normal direction of the calibration pattern plane, the ellipse center position can be used as the center of the calibration point. After the plane mapping test for the cross patterns of five points, many cross pattern groups can be accepted and all groups are combined to form a larger plane homography matrix.

Because the five-point groups decide the homography matrix H between calibration target and image plane, the matrix can guide the transformed position on image plane of remained points on the calibration target plane. The dotted circles on the image plane in Fig.5 present the candidate positions guided by the homography matrix H obtained from five point groups.

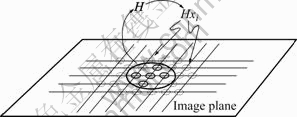
Fig.5 Five points group of cross-type pattern guiding transformed location of other points on calibration target plane

4 Experimental

In the experiments, the calibration pattern plate made of transparent and thin vinyl paper was used, and a CCD camera with image size of 1024×768 pixels with each pixel size of 4.5 μm×4.65 μm was used. This camera is connected to PC through IEEE1394 interface. Fig.1 shows the actual configuration of proposed system, as described in Ref.[17]. Navitar 12X zoom as magnification lens was used. The pattern for the camera calibration consists of round dots 1.0 mm in diameter, which was placed at a distance of 2.0 mm covering a region 140 mm×140 mm with black round dots on a transparent background of vinyl plate. The proposed method was tested for patterns with different backgrounds and uneven illumination. The image size was 1.024×768 pixels and the algorithm was implemented using C++ under a Windows XP environment.

Fig.6 shows the experimental result for the different illumination plates. The image with a clean background under controlled lighting gives a good calibration point extraction result. For the cluttered background image with uneven illumination, the adaptive threshold algorithm provides a reliable binary image, and probable calibration patterns that are not occluded by the objects on the plate are extracted. The paper sheet pattern is very easy to prepare for the camera calibration as it can be produced by a laser printer and a CAD system. Measurement accuracy by the CCD camera after calibration is under about 0.15 m from (16 mm/1024 pixels)×0.01 pixel calculated from the length of viewing size in horizontal region of the image and subpixel measurement resolution.

Fig.6 Extraction of calibration pattern for reference plate:    (a) Uneven brightness calibration pattern taken under irregular light variation with background cluttered objects; (b) Local adaptive binarization of image; (c) Results of calibration pattern extraction

With this resolution of image, to gain confidence in reliability of testing results, micro-tensile tests for the above described 5 specimens of BeNi were performed. For the digital image processing based approach using the CCD system, the eight black spots were marked on the surface of specimen at intervals of 1 mm using black pen. The force by load-cell and the extension between the grips by deflectometer were acquired at 10 points/s and the extension between black dots by the CCD camera system were acquired at 1 flame/s.

Fig.7 shows the comparison of load—extension curves of BeNi thin film by the delectometer and CCD system. The open triangle symbol shows the result by CCD system and the open circle symbol represents the result using capacitance type sensor (deflectometer). In Fig.7, difference exists between the curves because the initial length to be deformed is different. Fig.8 shows the comparison of stress—strain curves of BeNi thin film by the delectometer and CCD system. From comparison of mechanical properties in Fig.8, the elastic modulus (127 GPa), 0.2% off set yield strength (1 406 MPa) and ultimate tensile strength (1 528 MPa) by the CCD camera system are similar to the elastic modulus (129 GPa), 0.2% off set yield strength (1 390 MPa) and ultimate tensile strength (1 528 MPa) by the deflectometer, respectively. But difference exists in the fracture strain by the CCD camera system (0.055 22) and by the deflectometer (0.065 73). Through tests, it can be convinced that the proposed system could be effectively used in the tensile test of thin films at microscale and could describe more accurately plastic behavior of material of thin films than the delectometer (capacitance type sensor).

Fig.7 Comparison of load—extension curves of BeNi

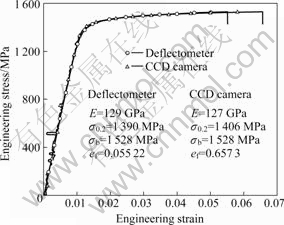
Fig.8 Comparison of stress—strain curves of BeNi

5 Conclusions

1) Camera calibration was the first step in a length measurement system using machine vision. A robust recognition method of a calibration pattern for camera calibration was presented. The digital image processing methods such as adaptive image binarization and plane homography were used to select correct calibration points and provide input data of the calibration. The method is very convenient and fully autonomous from the extraction of a calibration pattern and the corresponding information between a planar pattern and its image under conditions including uneven illumination and complicated backgrounds.

2) First, the original gray-scale image with unbalanced variation of intensity is binarized by an adaptive thresholding algorithm. Image labeling of the binary image regions provides the coordinate data of each calibration point. A plane homography test is then employed to detect a local set of calibration points among equally spaced round dot patterns. This point set then guides the extraction of other calibration points. A homography transformation was used to test the correspondence between image points and reference points on a calibration pattern. The experiment results show that the method is easy to use and the robust for pattern images has cluttered backgrounds taken under irregular lighting conditions. Measurement accuracy by the CCD camera after calibration is under about 0.15 μm from (16 mm/1024 pixels)×0.01 pixel calculated from the length of viewing size in horizontal region of the image and subpixel measurement resolution.

3) It is convinced that the proposed system could be effectively used in micro-tensile test of thin films at microscale and could describe more accurately plastic behavior of material of the thin films than the delectometer (capacitance type sensor).

Acknowledgement

This research was supported by a grant (08-K1401- 00610) from the Center of Nanoscale Mechatronics and Manufacturing, one of the 21st Century Frontier Research Programs which are supported by the Ministry of Education, Science and Technology in Korea, Industry-University Partnership Laboratory Supporting Business and also “New Professor Support Program from Seoul National University of Technology”.

References

[1] HARDWICK D A. The mechanical properties of thin films: a review [J]. Thin Solid Film, 1987, 154: 109-124.

[2] NIX W D. Mechanical properties of thin films [J]. Metal Trans A, 1989, 20: 2217-2245.

[3] TSUCHIYA T, TABATA O, SAKATA J, TAGA Y. Specimen size effect on tensile strength of surface micro-machined polycrystalline silicon thin-films [J]. Journal of Microelectromechanical System, 1998, 7(1): 106-113.

[4] ESPINOSA H D, PROROK B C, PENG B. Plasticity size effects in free-standing submicron polycrystalline FCC films subjected to pure tension [J]. Journal of Mechanical Physics Solids, 2004, 52: 667- 689.

[5] SHARPE J N. Mechanical properties of MEMS materials, the MEMS handbook [M]. New York: CRC Press, 2001.

[6] LARSEN K P, RASMUSSEN A A, et al. MEMS device for bending test: measurement of fatigue and creep of electroplated nickel [J]. Sensors and Actuators A, 2003, 103: 156-164.

[7] JOHANSSON S, SCHWEITZ J A, TENEZ L, TIREN J. Fracture testing of silicon micro-elements in situ in a scanning electron microscope [J]. Journal Appl Phys, 1988, 62(10): 4799-4803.

[8] KOMAI K, MINOSHIMA K, TAWARA H, INOUE S, SUNAKO K. Development of mechanical testing machine for micro-elements and fracture strength evaluation of single-crystalline silicon micro- elements [J]. Trans Jpn Sco Mech Eng, 1994, A 60/569: 52-58.

[9] BROMLEY E I, RANDALL J N, FLANDERS D C, MOUNTAIN R W. A technique for the determination of stress in thin-films [J]. Journal Vac Sci Technol, 1983, B 1(4): 1364-1366.

[10] TABATA O, KAWASHATA K, SUGIYAMA S, IGARASHI I. Mechanical property measurement of thin-films using load-deflection of composite rectangular membrane [C]// Proceedings of the IEEE Micro-Electro Mechanical Systems Workshop. 1988: 152-156.

[11] SHARPE J W. A new technique for measuring the mechanical properties of thin films [J]. Journal of Microelectromechanical Systems, 1997, 6: 193-199.

[12] CHASIOTIS I, KNAUSS W G. Microtensile tests with the aid of probe microsopy for the study of MEMS materials [C]// Proceedings of the SPIE. 2000: 96-103.

[13] LONG G S, READ D T, MCCOLSKEY J D, CRAGO K. Microstructual and mechanical characterization of electrodeposited gold films [S]. ASTM STP 1413. American Society of Testing and Materials, 2001: 262-277.

[14] SHARPE J W, PULSKAMP J, GIANOLA D S, EBERL C, POLCAWICH R G, THOMPSON R J. Strain measurements of silicon dioxide microspecimens by digital image processing [J]. Experimental Mechanics, 2007, 47: 649-658.

[15] MAZZA E, DANUSER G, DUAL J. Light optical deformation measurements in microbars with nanometer resolution [J]. Microsystems Technologies, 1996, 2: 83-91.

[16] OGAWA H, SUZUKI K, KANEKO S, NAKANO Y, ISHIKAWA Y, KITAHARA T. Measurements of mechanical properties of micro- fabricated thin films [C]// Proceedings of IEEE Tenth Annual International Conference on Micro Electro Mechanical Systems (MEMS’97). IEEE, 1997: 430-435.

[17] HA J E, PARK J H, KANG D J. New strain measurement method at axial tensile test of thin films through direct imaging [J]. Journal of Physics D: Applied Physics, 2008, 41: 175-406.

[18] WOLF C, JOLION J M. Extraction and recognition of artificial text in multimedia documents [EB/OL]. http://rfv.insalyon.fr/wolf/ papers/tr-rfv-2002-01.pdf. 2002.

[19] TRIER O D, JAIN A K. Goad-directed evaluation of binarization methods [J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1995, 17(12): 1191-1201.

[20] OTSU N. A Threshold selection method from gray-level histograms [J]. IEEE Trans on Systems, Man, and Cybernetics, 1979, SMC-9: 62-66.

[21] NIBLACK W. An introduction to digital image processing [M]. New York: Prentice Hall, 1986: 115-116,

[22] BALLARD D, BROWN C. Computer vision [M]. New York: Prentice-Hall, 1982.

[23] VIOLA P M, JONES J, SNOW D. Detecting pedestrians using patterns of motion and appearance [C]// Int Conf on Computer Vision. 2003: 734-741.

[24] HARTLEY R, ZISSERMAN A. Multiple view geometry [M]. London: Cambridge University Press, 2003.

[25] ZHANG Z. A flexible new Technique for camera calibration [J]. IEEE Trans Pattern Analysis and Machine on Intelligence, 2000, 22(11): 1330-1334.

[26] KIM J S, GURDJOS P, KWEON I S. Geometric and algebraic constraints of projective concentric circles and their applications to camera calibration [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(4): 637-642.3

Foundation item: Project(08-K141-00610) supported by the Center of Nanoscale Mechatronics and Manufacturing.

Corresponding author: Dong-Joong KANG; Fax: +82-51-514-1114; E-mail: djkang@pusan.ac.kr

(Edited by LONG Huai-zhong)