DOI: 10.11817/j.issn.1672-7207.2018.11.028
基于长期监测车流的公路桥梁设计车载模型校验
肖新辉1, 2,陈英3,鲁乃唯2
(1. 长沙理工大公路工程试验检测中心,湖南 长沙,410076;
2. 长沙理工大学 桥梁结构安全控制湖南省工程实验室,湖南 长沙,410114;
3. 中南林业科技大学 涉外学院,湖南 长沙,410004)
摘要:基于我国车流数据校验既有设计车辆荷载模型,提出随机车流荷载下桥梁车载效应极值外推方法。基于某高速公路桥梁动态称重系统长期监测车流数据,建立随机车流荷载模型,分析简支T梁桥的车辆荷载效应极值,据此校验国内外桥梁设计车辆荷载模型。研究结果表明:欧洲Eurocode3规范和英国BS5400规范的设计车辆荷载效应标准值远大于中国JTG D60—2015规范标准值和美国AASHTO荷载规范标准值;针对我国交通荷载现状,欧洲Eueocode3规范与英国BS5400规范设计车辆荷载模型的重现期趋于无穷大,而美国规范的重现期小于1 000 a,我国JTG D60—2015设计车道荷载规范的重现期为1 000~4 000 a。
关键词:桥梁工程;车辆荷载;极值;随机车流
中图分类号:U441+.4;U448.25 文献标志码:A 文章编号:1672-7207(2018)11-2861-07
Calibration of design vehicle load model of highway bridges based on long-term monitored traffic flow
XIAO Xinhui1, 2, CHEN Ying3, LU Naiwei2
(1. Institute of Communications Science, Changsha University of Science and Technology, Changsha 410076, China;
2. Hunan Province Engineering Laboratory of Bridge Structure Safety Control,
Changsha University of Science and Technology, Changsha 410114, China;
3. Foreign-related College, Central south University of Forestry and Technology, Changsha 410004, China)
Abstract: In order to calibrate the existing design vehicle load models based on the native vehicle load, an approach was presented for extrapolating extreme vehicle load effect of bridges under stochastic traffic flow loads. A stochastic traffic load model was established based on the long-term weigh-in-motion measurements of a highway bridge in China. The extreme traffic load effects of a simply supported T-girder bridge was analyzed. Based on the numerical results, several national and abroad design vehicle load models were calibrated. The results show that the standard values of the design vehicle load effect in Eurocode3 code and the British BS5400 code are much higher than those of Chinese JTG D60—2015 code and the British BS5400 codes. Based on the current traffic condition in China, the return period of the standard vehicle load model in Eurocode3 and Bridge BS5400 codes tend to be infinite. The return period of the American code is less than 1 000 a, while that of the Chinese JTG D60—2015 code is between 1 000-4 000 a.
Key words: bridge engineering; vehicle load; extreme value; random traffic flow
车辆荷载是公路桥梁可变荷载的重要组成部分,在公路桥梁设计结构验算中占主导地位。设计车辆荷载需要统计资料与实测数据制定。我国现行设计规范中的汽车荷载是“公路桥梁车辆荷载研究课题组”[1]于20世纪90年代初在我国4条四道的车流监测数据基础之上制定的。然而,自改革开放以来,我国交通运输行业迅速发展,交通量以及超载车辆迅速增大,超载车辆荷载下的桥梁安全事故屡见不鲜[2],亟待基于实测车流数据校验现行公路桥梁荷载标准值。设计规范中的交通荷载标准值是由多个地域的实测交通数据统计外推得出的,代表了一定重现期内的安全水平[3]。例如,美国AASHTO-LRFD规范基于1970年在Ontario等城市的交通测量数据为基准[4],欧洲Eurocode1规范的交通荷载标准值以1980年Auxerre等地区的测量值为基准[5]。我国公路桥梁汽车荷载设计标准值是20世纪90年代以河北等省份的4条高速公路的测量值基础上分析得出的。综合考虑交通运输行业发展迅速、交通运输管理不当的情况,既有设计规范可能高估桥梁生命周期内的安全水平。韩万水等[6]对河北某高速公路车流监测数据进行研究发现,少数特重车辆荷载工况使得桥梁强度超限率达15%。OBRIEN等[7]在欧洲4个动态称重(WIM)站点的测试结果也表明部分超载车辆对桥梁的作用已经超出设计值。为了克服设计车辆荷载模型在实际工程应用中的不足,国内外学者在车辆荷载模型及荷载效应进行了大量研究[8-11]。在交通荷载模型模拟方法方面,主要有基于实测数据的自然车队模拟方法、基于车辆参数概率统计的随机车流模拟方法和基于随机过程理论的平衡更新方法等[12]。在荷载的概率分布模型方面,早期的研究采用单一的概率分布类型(对数正态或Weibull分布等)拟合经验数据(轴质量、车距等)的概率密度函数。随着超载超限车辆的出现与增大,实测车质量呈现出多峰分布特征,混合分布模型(高斯混合模型、Weibull混合分布模型等)在此具有较好的适用性[13-15]。基于特定场地WIM数据的车辆荷载模型与设计活载模型的校验也是研究热点,例如阮欣等[16]基于我国WIM数据,考虑日交通量12万辆和重车混入率20%,建立了适用于多塔斜拉桥验算分析的车辆荷载加载模式。在交通荷载增长预测研究方面,目前的模型主集中在交通工程领域。基于长期监测的大数据模型是预测交通荷载增长的可靠基础,本文作者基于某高速公路桥梁WIM系统的长期统计车流监测数据,对车型、车质量、车距和车速等参数进行统计分析,采用合适的概率分布函数建立各参数的概率模型;介绍欧美国家与中国的公路桥梁汽车荷载设计模型,基于WIM数据统计的随机车流模型验证国内外设计规范的汽车荷载模型的适用性,研究交通量增长下既有桥梁汽车荷载设计规范的安全水平;基于极值理论与桥梁的可靠度水平校验既有桥梁汽车荷载设计模型。
1 国内外公路桥梁设计车载模型
1.1 美国设计车辆荷载模型
现行美国联邦州公路桥梁设计规范(AASHTO- LRFD)是NOWAK等[4]对美国车辆荷载进行大量调查与研究的基础上制定的,该荷载模型的原型是HS20-44模型。1944年,美国邦州公路桥梁设计规范(AASHTO)制定了HS20-44车辆荷载模型。该模型是总质量为24 t的三轴卡车,前中后轴的轴重力分别为26.8,106.6和106.6 kN,后轴轴距的变化范围为4.3~9.1 m,由影响线加载的最大效应确定。现行的AASHTO-LRFD荷载模型基于HS20-44模型制订,由双轴车或设计三轴卡车(见图1)与均布荷载的组合而成。其中,双轴车的轴重力为110 kN,间距为1.2 m;三轴卡车的轴重力分别为35,145和145 kN,均布荷载为9.3 kN/m。3车道与4车道的横向折减系数分别为0.90为0.75。该荷载模型的适用范围是跨度小于 152 m的桥梁,且若均布荷载效应较大,则应取消均布荷载效应。

图1 美国AASHTO-LRFD车辆荷载模型
Fig. 1 Vehicle load model of AASHTO-LRFD code in America
针对大跨度桥梁车辆荷载模型,美国土木工程协会(ASCE)在AASHTO-LRFD模型基础上提出建议荷载模型。该建议荷载模型在跨度为15.2~1 950.0 m的加载长度上采用集中力和均布荷载的方式加载,其中,集中力(P)变化范围是0~747 kN,均布荷载(U)根据重型车辆的占有率确定,如图2所示。针对多车道荷载效应,1车道全加载,2车道加载70%,余下的车道均加载40%。
1.2 欧洲ENV 1991荷载模型
欧洲公路桥梁交通荷载规范有4种荷载模型。荷载模型1(LM1)有2个子参数:双轴集中力和均布力,相关参数如表1所示[17]。每个荷载均有调整系数,与交通量和路线等有关。ENV的荷载模型2(LM2)为单轴荷载和均布荷载的组合。其中单轴荷载标准值为400 kN。荷载模型3和荷载模型4用于整体和局部验算,适用于短暂状态设计。欧洲ENV-LM2 车辆荷载模型见图3。

图2 美国ASCE车辆荷载模型
Fig. 2 Vehicle load model of ASCE in America
表1 欧洲ENV-LM1荷载模型的参数
Table 1 Parameters in load model of ENV-LM1 in European
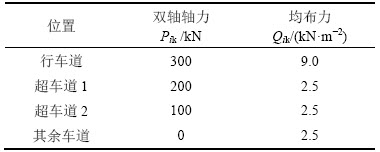

图3 欧洲ENV-LM2 车辆荷载模型
Fig. 3 Vehicle load model of ENV-LM2 in Eurocode3
1.3 英国BS5400荷载规范
英国BS5400荷载规范的公路桥梁交通荷载由HA和HB这2种荷载组合而成,基准期为120 a。其中,HA荷载由120 kN的集中荷载与均布荷载组成。当加载长度小于30 m时,均布荷载U=30 kN/m;当L>30 m时,U=151L-0.475 kN/m;但当桥梁跨度较大时,U不应低于9.0 kN/m;当跨径L<30 m时,应采用HA荷载描述双车道上每个车道紧密布置240 kN的车辆荷载。英国最新规范的均布荷载为
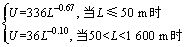
其中:L为桥梁荷载影响线中不利区域的所有长度的总和,而并非桥梁的跨径。车道宽度为3.65 m,针对大跨度桥梁,1车道和2车道的折减系数为1.0,其余车道的折减系数为0.6。需说明的是:HA荷载是英国设计规范的标准荷载,包含了英国境内的所有车辆荷载类型。
1.4 我国D60—2015桥梁汽车荷载模型
我国新版的JTG D60—2015“公路桥梁设计通用规范”采用公路-Ⅰ级和公路-Ⅱ级这2种荷载设计模型,根据桥梁所在公路等级进行划分。其中,高速公路、国道和一级公路及二级公路采用公路-Ⅰ级汽车荷载设计模型,其余采用公路-Ⅱ级荷载设计模型。该荷载在公路-Ⅰ的标准值基础之上乘以0.75的折减系数。公路-Ⅰ级车道荷载的加载图式如图4所示。

图4 我国D60—2015公路车道荷载模型
Fig. 4 Traffic lane loading model of D60—2015 code in China
图4所示的公路-Ⅰ级汽车荷载模型的集中力变化范围为270~360 kN,对应于桥梁变化范围为5~50 m;跨度大于50 m的桥梁的集中力标准值为50 m,均布荷载标准值为10.5 kN/m。集中力加载至桥梁影响线的最大值处,均布荷载加载至桥梁不利的影响线区域,在计算剪力时,集中荷载应乘以放大系数1.20。
除了车道荷载之外,我国公路桥涵设计通用规范还制定了标准车辆荷载,该车辆的横向布置如图5所示。在桥梁的车道数量大于3时,便考虑车辆荷载的横系折减,其中,第3,4和5车道的横向折减系数分别为0.78,0.67和0.60。

图5 我国JTG D60—2015车辆荷载模型
Fig. 5 Vehicle load model of JTG D60—2015 in China
通过分析上述各国的设计车辆荷载模型可以看出:每个国家的设计荷载标准有所不同,但车辆荷载的设计加载模式相似,主要表现在集中力加载和均布力加载方面。在标准车辆的轴质量方面,美国与中国的轴质量相似,约为14 t;英国的轴质量为22 t。
2 基于实测车流数据的桥梁极值分析方法
2.1 极值理论与标准值的关系
我国GB 50153—2008“工程结构可靠性设计统一标准”对可靠作用标准值的确定有明确规定。将车辆荷载作用看作平稳二项随机过程模型,则设计基准期内的最大值可采用简化的随机变量描述,大多数可变作用可假定为极值I型分布即Gumbel分布。基于平稳二项随机过程模型,设计基准期T内的最大值概率分布函数FT(t)可表示为[18]
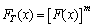 (2)
(2)
式中:F(x)为车辆荷载作用效应的截口分布;m为桥梁生命周期内该荷载效应的出现次数。可变作用的标准值Qk由设计基准期T内最大值概率分布特征值计算得出,即代表了荷载效应概率的P分布,表达式为
 (3)
(3)
此时,荷载作用效应的概率意义即为在桥梁设计生命周期内该数值被超载概率为1-P。
2.2 基于实测车流数据的桥梁极值外推方法
基于实测车流数据对大跨桥梁车载效应极值外推分析的关系步骤在于建立车辆荷载效应的极值概率模型FT(x)。为此,本文提出基于实测车流的极值概率分析框架,如图6所示。
图6的关键分析步骤如下:1) 对过滤后的车流监测数据进行统计分析;2) 采用Monte-Carlo抽样方法生成随机车流样本;3) 将随机车流加载至桥梁影响 线,计算随机车流作用下桥梁的日最大荷载效应值;4) 将大量的日最大荷载效应值放至Gubmel图中,由GEV(广义极值分布)函数对极值样本值进行拟合;5) 给定重现期,外推荷载效应极值,或者在给定设计标准值的前提下,对设计荷载效应的重期期进行校准。

图6 随机车流作用下桥梁极值外推分析框架
Fig. 6 Analytical framework of extrapolation of extreme load effect of bridges under stochastic traffic load
需说明的是:由于桥梁结构荷载效应分析采用了静力影响线方法,其计算耗时可忽略。采用尽可能多的随机车流样本数据(如1 000 d)以提高GEV函数拟合与外推精度。
3 算例分析
为了分析模拟随机车流与各国规范作用于中大跨径桥梁的荷载效应标准值,选取20~40 m的T梁桥为工程背景,分析实测交通荷载作用,模拟随机车流荷载效应值特征,据此校验各国设计车辆荷载模型。
3.1 车流监测数据
本文所采用的WIM系统数据来源于四川省某高速公路的WIM系统[19-20]。自2012年开始,该系统已监测5 a的车流数据。2017年的日平均车流量约为8 500辆,货车占有率约为12%,货车超载率约为21%。对该数据进行筛选与统计分析,将车辆划分为6种车型,根据车距划分密集车流和稀疏车流。图7所示为6轴货车总重力与密集车距的概率分布。
图7中,6轴货车总重力由3参数的高斯混合模型拟合,车距的概率分布由Gamma分布函数拟合。
3.2 简支T梁桥内力分析
交通运输部的“公路桥梁通用图”中,装配式PC简支T梁桥的结构尺寸如图8所示,其中,Hb为主梁高度。考虑横向双车道荷载效应,由各国设计规范计算的1号梁的弯矩效应标准值(Qk)如表2与图9所示。

图7 6轴货车总重力与密集车距
Fig. 7 Gross weight of 6-axle truck and vehicle spacing of dense traffic

图8 简支梁的结构尺寸图
Fig. 8 Dimensions of structure of simply supported beam
表2 简支T梁桥的车辆荷载弯矩标准值
Table 2 Standard bending moment of vehide load on simply supported T-girder bridge kN·m

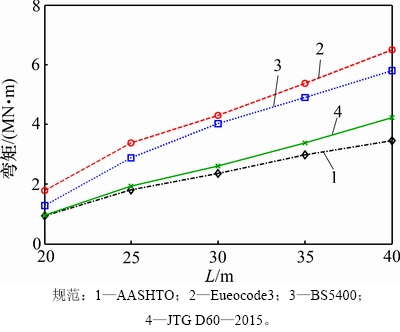
图9 简支T梁桥的设计车辆荷载效应标准值
Fig. 9 Standard value of design vehicle load effect of simply supported Tgrder bridge
从表2与图8可知:各国车辆荷载设计模型的标准值对T梁产生的弯矩变化趋势相同,且随着跨径增大,弯矩效应的标准值逐步增加。但各荷载效应标准值有所不同,主要表现在:欧洲Eueocode3规范和英国BS5400规范的荷载效应标准值远大于中国JTG D60-2015规范和美国AASHTO荷载规范值。
采用如图6所示的分析方法,计算实测车流作用下1号梁的弯矩,如图10所示。

图10 简支T梁桥跨中弯矩时程曲线(L=40 m)
Fig. 10 Time history of mid-span point of simply supported T girder bridge when L=40 m
3.3 简支T梁桥的极值概率分析
基于如图10所示的车流荷载效应分析结果,取1 000 d的随机样本最大值,拟合GEV分布函数,如图11所示。其中,极值概率曲线参数为:形状参数k=0.278,位置参数μ=3215,尺度参数σ=658。
由图11可知:GEV分布函数的拟合曲线与日最大样本值较吻合,表明拟合的极值分布函数能够代表样本点进行外推分析。1 000 a重现期对应于Gumbel累积分布函数值为12.43,对应于100 a内的概率约为90%,外推极值为4 260 kN·m。

图11 极值分布与外推
Fig. 11 Extreme value distribution and extrapolation
根据如图11所示的GEV函数,对各国设计车辆荷载效应标准值进行校验,可得到表2中标准值对应的概率分布函数,即可转换为如表3所示的重现期。
表3 设计车辆荷载效应的重现期
Table 3 Return period of design vehicle load a

分析表3可知:欧洲规范的设计车辆荷载的重现期最大,设计最保守;英国规范的设计车辆荷载的重现期次之,设计较保守;美国规范的设计车辆荷载重现期最小,小于1 000 a;我国设计车辆荷载模型的重现期介于1 000~5 000 a,小跨径桥梁重现期较小,而大跨径桥梁的重现期较大。
为了分析设计车辆荷载标准值的概率保证水平,将如表3所示的车辆荷载效应重现期转换为桥梁运营期(100 a)的失效概率,如表4所示。
在我国实测车流荷载作用的概率模型下,各国规范的汽车荷载标准值的重现期和设计基准期内的概率保证水平有所不同,主要表现在:欧洲Eueocode3规范和英国BS5400规范设计较保守,而美国规范的设计荷载偏于不安全,我国荷载规范的可靠概率为92.5%~97.8%。事实上,各国设计规范的荷载模型均由当地的汽车荷载概率特征制定,基于我国的车流统计数据对国外设计荷载规范的校验结果仅用于对比分析。
表4 简支T梁桥车辆荷载弯矩标准值的可靠概率
Table 4 Probability level of standard value of simply supported T-girder bridges under vheicle loads

4 结论
1) 随机车流荷载模型包含实际车流的概率信息,可用于建立桥梁车载效应极值概率模型,为校验国内外车辆荷载模型提供了保障。
2) 欧洲Eueocode3规范和英国BS5400规范的设计车辆荷载效应标准值远大于中国JTG D60—2015规范和美国AASHTO荷载规范值,随着桥梁跨径增加,车辆荷载效应差异更加明显。
3) 针对我国交通荷载现状,欧洲Eueocode3规范与英国BS5400规范设计车辆车辆荷载模型的重现期趋于无穷大,而美国规范的重现期小于1 000 a,我国JTG D60—2015的设计车道荷载规范的重现期为1 000~4 000 a。
本文仅采用国内某高速公路的监测数据,有待采用多个省份的监测数据校准本文的分析结果。此外,有待进一步研究车辆-桥耦合振动对荷载效应极值外推结果的影响。
参考文献:
[1] 公路桥梁车辆荷载研究课题组. 公路桥梁车辆荷载研究[J]. 公路, 1997(3): 8-12.
Workshop of Vehicle Load Effect on Highway Bridges. Research on vehicle load effect on highway bridges[J]. Highway, 1997(3): 8-12.
[2] 鲁乃唯, 刘扬, MOHAMMAD N. 交通量持续增长下大跨桥梁时变极值外推分析[J]. 工程力学, 2018, 35(7): 159-166.
LU Naiwei, LIU Yang, MOHAMMAD N. Extrapolation of time-variant extreme effect on long-span bridge considering steadily growing traffic volume[J]. Engineering Mechanics, 2018, 35(7): 159-166.
[3] 杨晓艳, 贡金鑫, 冯云芬. 不同跨径桥梁车辆荷载分项系数及可靠度[J]. 中国公路学报, 2015, 28(6): 59-66.
YANG Xiaoyan, GONG Jinxin, FENG Yunfen. Partial factors of vehicle loads and reliability analysis of bridges with different spans[J]. China Journal of Highway and Transportation, 2015, 28(6): 59-66.
[4] NOWAK A S, LUTOMIRSKA M, FIS I. The development of live load for long span bridges[J]. Bridge Structures, 2010, 6(1): 73-79.
[5] CAPRANI C C. Calibration of a congestion load model for highway bridges using traffic microsimulation[J]. Structural Engineering International, 2012, 22(3): 342-348.
[6] 韩万水, 武隽, 马麟, 等. 基于微观交通流模型的风-车-桥系统高真实度模拟[J]. 中国公路学报, 2015, 28(11): 37-45.
HAN Wanshui, WU Jun, MA Lin, et al. High-fidelity simulation of win-vehicle-bridge system based on microscopic traffic load model[J]. China Journal of Highway and Transport, 2015, 28(11): 37-45.
[7] OBRIEN E J, ENRIGHT B. Modeling same-direction two-lane traffic for bridge loading[J]. Structural Safety, 2011, 33(4): 296-304.
[8] 李植淮, 李春前, 孙健康, 等. 基于GPD模型的车辆荷载效应极值估计[J]. 工程力学, 2012, 29(S1): 166-171.
LI Zhihuai, LI Chunqian, SUN Jiankang, et al. Estimating extreme vehicle load effect based on GPD model[J]. Engineering Mechanics, 2012, 29(S1): 166-171.
[9] 张征文, 杨飞, 赵建峰, 等. 基于WIM数据的简支梁桥车辆荷载效应分析[J]. 公路交通科技, 2014, 31(5): 86-92.
ZHANG Zhengwen, YANG Fei, ZHAO Jianfeng, et al. Analysis on traffic load effect of simply supported beam bridge based on WIM data[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 86-92.
[10] RUAN X, ZHOU J, CAPRANI C. Safety assessment of the antisliding between the main cable and middle saddle of a three-pylon suspension bridge considering traffic load modeling[J]. Journal of Bridge Engineering, 2016, 21(10): 04016069.
[11] LEAHY C, OBRIEN E, O’CONNOR A. The effect of traffic growth on characteristic bridge load effects[J]. Transportation Research Procedia, 2016, 14: 3990-3999.
[12] 夏樟华, 陈俊民, 宗周红, 等. 并道运行状态下高速公路桥梁车辆荷载效应[J]. 长安大学学报(自然科学版), 2017, 37(1): 76-84.
XIA Zhanghua, CHEN Junmin, ZHONG Zhouhong, et al. Vehicle load effect of expressway bridge in the state of lanes merging[J]. Journal of Chang’an University(Natural Science Edition), 2017, 37(1): 76-84.
[13] 鲁乃唯, 罗媛, 汪勤用, 等. 车载下大跨度悬索桥梁动力可靠度评估[J]. 浙江大学学报(工学版), 2016, 50(12): 9-16.
LU Naiwei, LUO Yuan, WANG Qinyong, et al. Dynamic reliability assessment for long-span bridges under vehicle load[J]. Journal of Zhejiang University(Engineering Science), 2016, 50(12): 9-16.
[14] 刘浪, 尤吉. 公路桥梁车辆荷载效应的外推计算[J]. 土木工程学报, 2015, 48(4): 59-64.
LIU Lan, YOU Ji. Extrapolation method for truck load effects on highway bridges[J]. China Civil Engineering Journal, 2015, 48(4): 59-64.
[15] ENRIGHT B, CAREY C, CAPRANI C C. Microsimulation evaluation of Eurocode load model for American long-span bridges[J]. Journal of Bridge Engineering, 2013, 18(12): 1252-1260.
[16] 阮欣, 周军勇, 石雪飞, 等. 公路桥梁长加载区间的多车道车辆荷载概念模型[J]. 同济大学学报(自然科学版), 2015, 43(10): 1497-1502.
RUAN Xin, ZHOU Junyong, SHI Xuefei, et al. Conceptual traffic load model for multilane highway bridges with long loading length[J]. Journal of Tongji University(Natural Science Edition), 2015, 43(10): 1497-1502.
[17] OBRIEN E, BORDALLO-RUIZ A, ENRIGHT B. Lifetime maximum load effects on short-span bridges subject to growing traffic volumes[J]. Structural Safety, 2014, 50: 113-122.
[18] ENRIGHT B, OBRIEN E J. Monte Carlo simulation of extreme traffic loading on short and medium span bridges[J]. Structure & Infrastructure Engineering, 2012, 9(12): 1-16.
[19] 刘扬, 鲁乃唯, 邓扬. 基于实测车流的钢桥面板疲劳可靠度评估[J]. 中国公路学报, 2016, 29(5): 58-66.
LIU Yang, LU Naiwei, DENG Yang. Fatigue reliability assessment of steel bridge decks under monitored traffic loads[J]. Journal of Highway and Transport, 2016, 29(5): 58-66.
[20] 鲁乃唯, 刘扬, 邓扬. 随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估[J]. 中南大学学报(自然科学版), 2015, 46(11): 4300-4306.
LU Naiwei, LIU Yang, DENG Yang. Fatigue damage and life assessment for steel decks of suspension bridge under stochastic traffic flow[J]. Journal of Central South University(Science and Technology), 2015, 46(11): 4300-4306.
(编辑 陈灿华)
收稿日期:2017-11-12;修回日期:2018-01-22
基金项目(Foundation item):国家重点基础研究发展计划(973计划)项目(2015CB057705);国家自然科学基金资助项目(51308073);长沙理工大学桥梁工程领域开放基金资助项目(18KD02) (Project(2015CB057705) supported by the National Basic Research Program(973 Program) of China; Project(51308073) supported by the National Natural Science Foundation of China; Project(18KD02) supported by the Opening Fund in Bridge Engineering of Changsha University of Science and Technology)
通信作者:陈英,硕士,讲师,从事结构可靠度评估研究;E-mail: 879229586@qq.com