DOI: 10.11817/j.issn.1672-7207.2015.11.003
Q345B宽厚板微观组织优化数值模拟
高向宙,李京社,杨树峰
(北京科技大学 冶金与生态工程学院,北京,100083)
摘要:为改善Q345B宽厚板中心偏析缺陷,采用CAFE法对连铸凝固末端的铸坯断面微观组织进行模拟计算,研究钢水过热度和铸坯拉速对凝固组织的影响规律。研究结果表明:适当减小过热度和降低拉速能够提高中心等轴晶率,增加晶粒数,减小晶粒平均半径。当钢水过热度由34 ℃降低至25 ℃,拉速由0.68 m/min调整到0.56 m/min后,断面凝固组织中心等轴晶率增加15.1%,晶粒平均半径减小2 135 μm,晶粒数增加367.4%,且模拟组织与试验铸坯得到的微观组织形貌基本一致,铸坯中心偏析缺陷也得到有效改善。
关键词:宽厚板;中心偏析;连铸工艺;微观组织;数值模拟
中图分类号:TF777.2 文献标志码:A 文章编号:1672-7207(2015)11-3991-08
Numerical simulation on optimization of microstructure on Q345B wide and heavy plate
GAO Xiangzhou, LI Jingshe, YANG Shufeng
(School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing,
Beijing 100083, China)
Abstract: In order to improve the centerline segregation of Q345B wide and heavy plate, the microstructure of the cross section of casting blank was obtained by CAFE approach. And the influence of the superheat and casting speed on the microstructure of billet was analyzed. The results show that decreasing the superheat and casting speed properly can increase the isometric crystal rate and the number of grains, and decrease the average radius. After adjusting the superheat from 34 ℃ to 25 ℃ and casting speed from 0.68 m/min to 0.55 m/min in ProCAST, the center equiaxial crystal rate increases about 15%, the average grain radius decreases by 2 135 μm, and the number of grains increases about 367.4%, which is basically identical with the microstructure statistical data of experimental billet. The centerline segregation of billet gets improved effectively.
Key words: wide and heavy plate; centerline segregation; continuous casting process; microstructure; numerical simulation
Q345B钢是国内低合金钢中产量最大的钢种,也是用于汽车大梁板的专用中厚板,要求其各向异性小,内部组织均匀等。大多数用于生产汽车大梁板的连铸坯都存在中心偏析,这必然造成钢板沿厚度方向冶金质量和性能的不均匀性,显著降低钢材的伸长率,从而对钢板的使用性能产生较大的影响。因此,改善Q345B钢宽厚板的中心偏析具有十分重要的意义。近年来,冶金界对于改善连铸坯中心偏析研究较多,如常桂华等[1]通过对连铸板坯的硫印数据库统计分析,证明了过热度、拉速、铸坯宽度增加均不利于改善铸坯中心偏析;赖朝彬等[2]通过调整拉速、二冷比水量、过热度等连铸工艺参数,减小铸坯横断面二次枝晶臂间距,来减轻中心碳偏析;研究最终认为采取提高钢水洁净度、低过热度浇注、低拉速、电磁搅拌、轻压下和优化二冷技术等措施是减轻连铸坯中心偏析的有效途径。目前改善连铸坯偏析的研究方法仍以“工艺调整—取样分析”为主,通过工业试验来改善铸坯内部缺陷的方法具有周期长、代价高等缺点,而数值模拟法凭借其成本低、周期短、见效快等优点,使得越来越多的研究者倾向于利用数值模拟对铸坯微观组织进行分析和研究。目前对铸坯凝固组织模拟应用最广泛的是ProCAST软件中的CAFE模块,最早由Rappaz等[3-6]利用此方法模拟了从柱状晶到等轴晶的转变,并在试验中得到了验证;Wang等[7-9]应用CAF 模型耦合了钢液浇注、温度场、流场、缩孔、疏松,实现了对易切削钢9SMn28铸件微观组织的模拟;白李国等[10]也曾利用该方法成功实现了对金属凝固组织形成的数值模拟。但这些研究都只针对于模铸或者连铸方坯和圆坯,对于板坯连铸凝固过程微观组织的研究仍属罕见。为此,本文作者通过对某厂宽厚板中心偏析的情况进行系统调研,采用ProCAST商业软件对370 mm×2 120 mm宽厚板凝固过程中的温度场变化进行计算,并在此基础上运用CAFE法对连铸坯横截面的微观组织进行模拟,使得凝固过程中等轴晶的形成和柱状晶的生长实现可视化,通过对模型中工艺参数进行调整,最终实现铸坯截面的等轴晶和柱状晶比例合理化,达到改善铸坯中心偏析缺陷的目的。
模型耦合了钢液浇注、温度场、流场、缩孔、疏松,实现了对易切削钢9SMn28铸件微观组织的模拟;白李国等[10]也曾利用该方法成功实现了对金属凝固组织形成的数值模拟。但这些研究都只针对于模铸或者连铸方坯和圆坯,对于板坯连铸凝固过程微观组织的研究仍属罕见。为此,本文作者通过对某厂宽厚板中心偏析的情况进行系统调研,采用ProCAST商业软件对370 mm×2 120 mm宽厚板凝固过程中的温度场变化进行计算,并在此基础上运用CAFE法对连铸坯横截面的微观组织进行模拟,使得凝固过程中等轴晶的形成和柱状晶的生长实现可视化,通过对模型中工艺参数进行调整,最终实现铸坯截面的等轴晶和柱状晶比例合理化,达到改善铸坯中心偏析缺陷的目的。
1 CAFE模型的介绍
随着连铸凝固理论的发展和成熟,越来越多的科研工作者开始热衷于对凝固组织的研究,而且数值模拟技术的发展也实现了凝固组织生长的可视化,与此同时,许多用来模拟金属凝固组织的计算方法也相继提出,如确定性方法、随机性方法、相场方法等[11-12],其中随机性方法是采用概率方法来研究凝固过程中晶粒的形核和长大,包括形核位置的随机分布和晶粒的随机取向,其主要特点是建立形核和枝晶生长动力学及结晶取向物理机制,实现动态显示每个晶粒的具体形态及生长演变[13]。金属实际凝固过程中的传质过程以及能量和结构起伏等都是随机的,所以,随机性方法更容易受到人们的青睐。
元胞自动机(cellular automation,CA)方法既是随机法的一种,它是一种时间、空间、状态都离散的动力学模型。在凝固模拟过程中,它基于形核的物理机制和晶体生长动力学理论,用随机性原理处理晶核分布和结晶方向,从而模拟凝固过程的微观组织。CA法模拟不依赖于计算过程中的单元网格划分结构,具有计算速度快,计算区域大等特点,这也使它很适合于描述自由枝晶、柱状枝晶的形成以及柱状晶与等轴晶直接的转化[14-15]。随着模拟技术的不断发展,到20世纪90年代,Gandin等[16]将元胞自动机模型与有限元方法(FE)耦合起来建立了宏观-微观的元胞自动机模型,即CAFE法,它的优势具体表现为凝固区域首先用较粗的网格(即FE)来计算温度场,在此网格内划分成更细而均匀的节点,节点的温度通过插值函数获得,在其中采用CA模型进行形核与生长计算,这样就可以大大节省内存和计算时间。
1.1 形核模型
本文采用Rappaz等[3]提出的基于高斯分布的连续形核模型,在某一给定的过冷度△T条件下,其形成的晶粒密度n(△T)可通过对该分布曲线的积分求得
 (1)
(1)
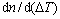 由高斯分布[17]确定:
由高斯分布[17]确定:
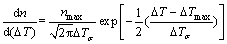 (2)
(2)
式中: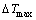 为平均形核过冷度;
为平均形核过冷度; 为形核过冷度标准方差;nmax为正态分布从0到
为形核过冷度标准方差;nmax为正态分布从0到 积分得到的最大形核密度。
积分得到的最大形核密度。
1.2 枝晶生长模型
实际凝固过程中,晶体的生长是依靠液体中的过冷度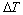 实现的,该过冷度可由以下4个方面的能量构成。
实现的,该过冷度可由以下4个方面的能量构成。
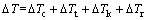 (3)
(3)
式中: ,
,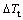 ,
, 和
和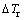 分别为成分过冷度、热力学过冷度、生长动力学过冷度和固-液界面曲率过冷度。在绝大多数情况下,后3项相对于
分别为成分过冷度、热力学过冷度、生长动力学过冷度和固-液界面曲率过冷度。在绝大多数情况下,后3项相对于 来说太小,计算时常常将其忽略。根据KGT模型[18],枝晶尖端半径R、生长速度v可满足以下关系:
来说太小,计算时常常将其忽略。根据KGT模型[18],枝晶尖端半径R、生长速度v可满足以下关系:
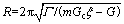 (4)
(4)
 (5)
(5)
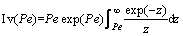 (6)
(6)
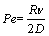 (7)
(7)
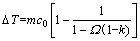 (8)
(8)
式中: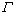 为固液界面的界面能与每体积熔化区的熵的比值,即Gibbs-Thompson系数;m为液相线斜率;Gc为枝晶前沿液相中的溶质浓度梯度;
为固液界面的界面能与每体积熔化区的熵的比值,即Gibbs-Thompson系数;m为液相线斜率;Gc为枝晶前沿液相中的溶质浓度梯度;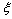 为贝克来数Pe的函数,在低速生长时取1;G为温度梯度;
为贝克来数Pe的函数,在低速生长时取1;G为温度梯度; 为溶质过饱和度;c*为枝晶尖端液相浓度;c0为合金溶质浓度;Pe为溶质的贝克来数,用来表示对流与扩散的相对比例;
为溶质过饱和度;c*为枝晶尖端液相浓度;c0为合金溶质浓度;Pe为溶质的贝克来数,用来表示对流与扩散的相对比例;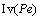 为贝克来数Pe的Ivantsov函数;D为液相内的溶质扩散系数;
为贝克来数Pe的Ivantsov函数;D为液相内的溶质扩散系数;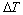 为枝晶尖端的过冷度;k为平衡分配系数。
为枝晶尖端的过冷度;k为平衡分配系数。
将式(4)~(8)联立,可得枝晶尖端生长速度v和过冷度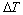 之间的关系。对KGT模型拟合之后,得到如下枝晶尖端生长速度的三次多项式:
之间的关系。对KGT模型拟合之后,得到如下枝晶尖端生长速度的三次多项式:
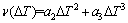 (9)
(9)
式中:a2和a3为拟合多项式的系数;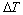 为枝晶尖端总过冷度。
为枝晶尖端总过冷度。
2 Q345B连铸坯凝固组织的模拟
2.1 模型参数的确定
该模型是以某特钢厂生产的特宽特厚板为研究对象建立的,模型与实际铸坯尺寸比例为1:1,横断面 (长×宽)为2 120 mm×370 mm,钢种为Q345B钢,钢种化学成分如表1所示,连铸的基本工艺参数如表2所示。
应用ProCAST软件中运动坐标系的二维切片法,对铸坯的凝固过程温度场和断面凝固率进行仿真数值模拟,即在铸坯拉速方向上,截取一段厚为10 mm的薄片作为研究对象(如图1所示),采用四面体网格划分,建立二维非稳态模型,研究了该薄片从结晶器弯月面开始,以拉坯速度依次经过结晶器、二冷区,直到在空冷区完成凝固的热量散失过程。
表1 Q345B钢化学成分(质量分数)
Table 1 Chemical composition of Q345B steel %
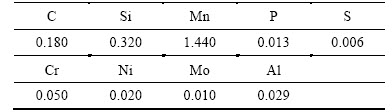
表2 连铸基本工艺参数
Table 2 Basic parameters of continuous casting technology
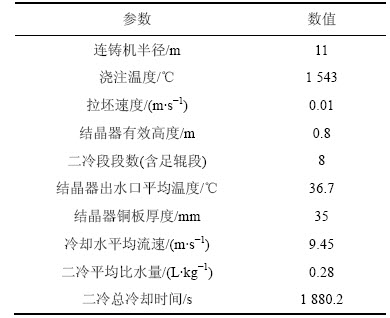
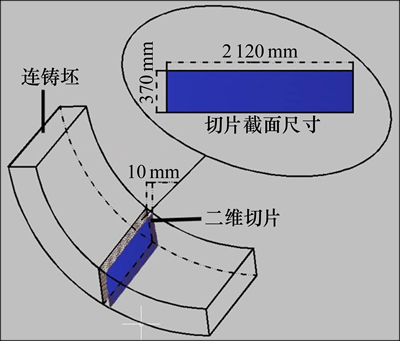
图1 二维切片法示意图
Fig. 1 Schematic diagram of 2-D slice theory
图2所示为断面凝固率随时间的变化曲线。由图2可以看出:在总凝固时间达到3 017.7 s时,铸坯横截面的凝固率刚好为100%,计算得出铸坯凝固末端距离弯月面的距离是30.2 m,而通过射钉实验测出现场连铸坯实际凝固末端的位置是29.9 m,模拟值的相对误差仅为0.99%,这说明模拟的计算结果与实际生产的理论计算结果基本一致。
在连铸坯的凝固末端截取一段厚为10 mm的断面,采用ProCAST软件中的CAFE模型进行对其凝固组织进行数值模拟,为节省计算时间,本文只取断面的左半部分进行模拟,且文中所有关于晶粒度和等轴晶率的统计数据均只对应铸坯的左断面。其中Gibbs-Thompson系数[19]取3×10-7 m·K;体平均形核过冷度和过冷度偏差为△Tv,max=2.5 K,△Tv,σ=0.1 K;面平均形核过冷度和过冷度偏差为△Ts,max=0.5 K,△Ts,σ=0.1 K,最大形核密度Nv,max=5×1010,Ns,max=5×108。将主要溶质元素参数(见表3)输入CAFE模型中,计算得到枝晶尖端生长动力学参数为a2=2.858× 10-8,a3=9.513×10-4。
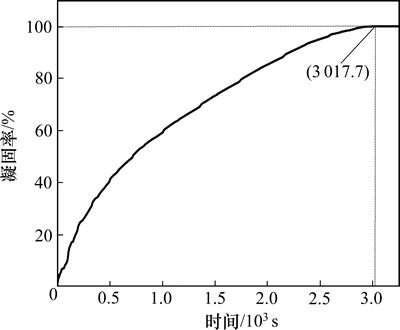
图2 断面凝固率随时间的变化曲线
Fig. 2 Relationship of solid fraction change with time of cross section on casting blank
2.2 优化前模型结果的验证
基于生产现场提供的连铸工艺参数和模型中设置的CAFE参数,通过软件模拟出的凝固末端铸坯微观组织形貌如图3(a)所示,试验铸坯样品经过酸洗后的低倍组织如图3(b)所示,可以确定模拟结果和试验铸坯凝固组织形貌基本吻合。
从图3(b)可以明显地辨别出激冷层、柱状晶区和中心等轴晶区。这是由于钢液在结晶器中受到急冷的作用,在铸坯的表层迅速形成一层细小等轴晶,即激冷层区;铸坯从结晶器出来后进入二冷区,这时由于凝固坯壳的热阻效应,铸坯内部向外传热能力下降,开始产生定向结晶,促使柱状晶迅速生长,产生柱状晶区;柱状晶生长到一定程度,冷却速度进一步下降,此时内部钢液成分和温度基本统一,新产生的晶粒阻碍柱状晶生长,形成中心粗大等轴晶带。
表3 主要溶质元素参数
Table 3 Main parameters of solute elements
铸坯的这种凝固组织结构和形貌对铸坯中心偏析程度有重要影响。田陆等[20]研究表明:当铸坯柱状晶晶体细小,且等轴晶面积狭窄(<10%)时,中心偏析程度最严重,最终将导致铸坯内部缺陷难以控制。其认为柱状晶越是粗大发达,晶间间隙越大,且当一次枝晶间隙大于二次枝晶臂长2倍时,高溶质钢液均停留在枝晶之间的间隙内,最终凝固时,高溶质钢液并没有汇聚到铸坯中心,中心偏析不会严重;而对于柱状晶晶粒细小的铸坯,由于枝晶间的间隙很小,易偏析元素会随着凝固界面均一地向前推进,偏析元素均富集到铸坯中心处,造成中心偏析严重;当铸坯凝固组织中有较宽的等轴晶区时,由于等轴晶的凝固界面没有方向性,有效地分散了中心区域的溶质元素,改善了中心偏析。综上可知:在不改变钢液成分的前提下,减轻铸坯中心偏析的本质就是要改善铸坯的凝固组织,使柱状晶晶体变得粗大,或者增大等轴晶面积均是改善中心偏析的有效措施。
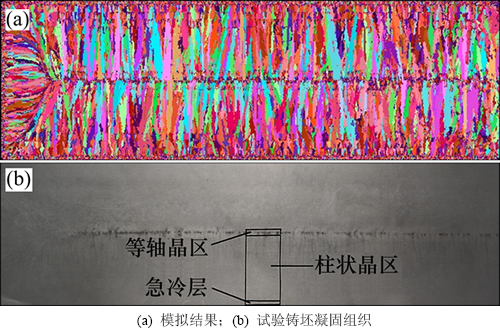
图3 优化前模拟结果和试验铸坯凝固组织形貌对比
Fig. 3 Comparison between simulation and experimental results before optimization
从图3可以看出:铸坯凝固组织中的柱状晶组织表现为细长型;应用Image Pro-Plus图像处理软件对模拟结果进行分析得到,铸坯凝固组织中的等轴晶率为8.4%,而中心等轴晶率仅为6.4%;由以上分析结果可知:铸坯的凝固组织形貌符合“柱状晶晶体细小,等轴晶面积狭窄,中心偏析严重”的特点,本文将通过利用增大中心等轴晶率的方法来改善铸坯中心偏析缺陷。
2.3 模拟优化结果及讨论
2.3.1 过热度的模拟优化结果及讨论
钢水过热度是保证连铸产量和铸坯质量的关键工艺参数之一,从理论上讲,低过热度有利于低温度梯度的形成,加之低过热度的钢液内储备有大量的晶胚,对获得高等轴晶率是非常有利的。鉴于此,本文基于现场实际生产情况,选择过热度为34,29,24和19 ℃进行模拟,优化前钢水过热度为34 ℃,其他工艺参数均保持不变。模拟结果如图4所示。
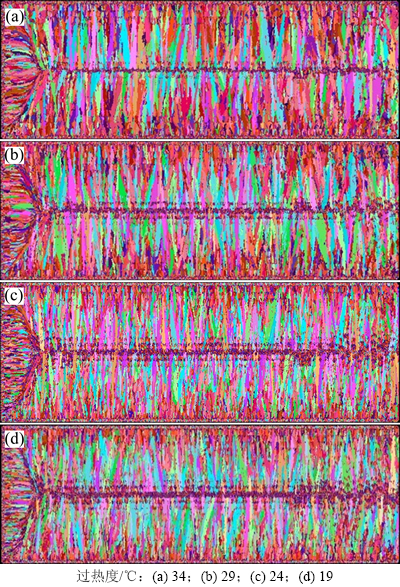
图4 不同过热度下铸坯微观组织模拟结果
Fig. 4 Simulated microstructure at different superheats
用Calcosoft-3D软件分析晶粒度,Image Pro-Plus软件分析中心等轴晶率,结果如图5所示。由图5可以看出:随着钢水过热度的逐渐降低,模拟结果中凝固组织的晶粒呈逐渐细化的趋势,具体表现为:当过热度由34 ℃下降到19 ℃时,晶粒数由原来的24 451个增加到了54 059个,晶粒平均半径由2 432 μm减小到1 285 μm,中心等轴晶率则由6.4%增加到了12.3%,其中过热度由29 ℃变化到24 ℃时,晶粒数、晶粒平均尺寸和中心等轴晶率的变化幅度最大,分别为31.9%,23.6%和31.3%,中心等轴晶率得到了明显提高。分析原因可得:1) 当钢液拥有较低的过热度时,结晶前沿形成的成分过冷区就会变得很大,这样就更有利于等轴晶的产生,从而抑制柱状晶的生长;2) 钢液过热度降低后,其中游离的晶粒就容易保存下来,且随着晶粒数的增多以及个体的长大,柱状晶生长便会受到抑制;3) 绕注温度的变化必然导致形核参数发生变化,这是因为低温的钢液中形核基底数必然多于高温的钢液,这也将促使最大形核密度参数增大,最终导致模拟结果中中心等轴晶率的提高。
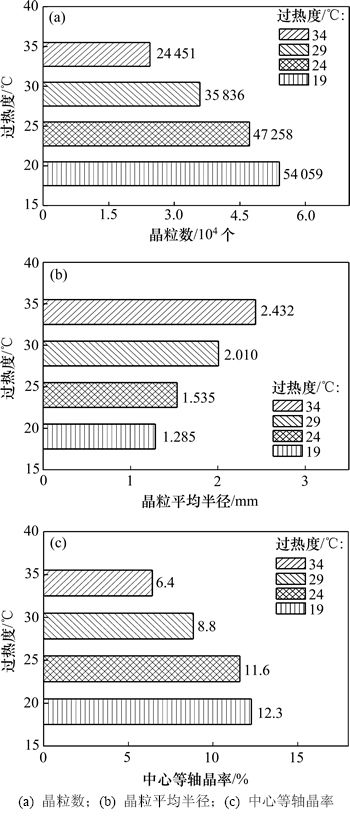
图5 不同过热度条件下的模拟统计结果
Fig. 5 Simulated statistical results at different superheats
2.3.2 拉速的模拟优化结果及讨论
一般来说,适当降低拉速对改善铸坯内部质量有利,可使铸坯在离开结晶器时,能够拥有足够厚度的凝固坯壳用以承受内部钢液的静压力,防止压力过大出现鼓肚。本文基于现场生产实际情况,选择铸坯拉速为0.68,0.64,0.60和0.55 m/min进行模拟,优化前铸坯拉速为0.68 m/min,在此需要说明的是,实际生产中为满足工艺要求,拉速降低时,冷却强度也要随之减小。模拟结果如图6所示。用2.3.1节中的计算方法,对铸坯凝固组织晶粒度和中心等轴晶率进行分析,结果见图7 。
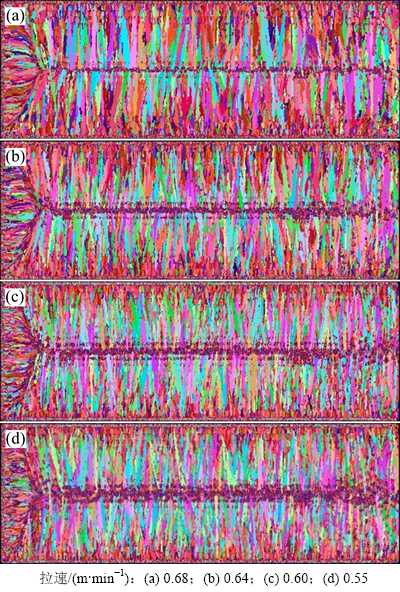
图6 不同拉速下铸坯微观组织模拟结果
Fig. 6 Simulated microstructure at different casting speeds
由图7可知:当拉速由0.68 m/min减小到0.55 m/min时,晶粒数由24 451个增加到81 416个,晶粒平均半径由2 432 μm减小到703 μm,中心等轴晶率则由6.4%增加到了16.9%,其中拉速由0.60 m/min变化到0.55 m/min时,晶粒数、晶粒平均尺寸和中心等轴晶率的变化幅度最大,分别为50.9%,45.9%和40.6%。对原因进行分析:1) 当拉速减小时,钢水在结晶器中的停留时间就会延长,进而使转移钢液过热量所需时间相对减少,促进了中心等轴晶的生成,限制了柱状晶的发展;2) 拉速降低,冷却强度随之减弱,这将使形核参数中的平均形核过冷度减小,形核变得相对容易,最终将增大中心等轴晶率。
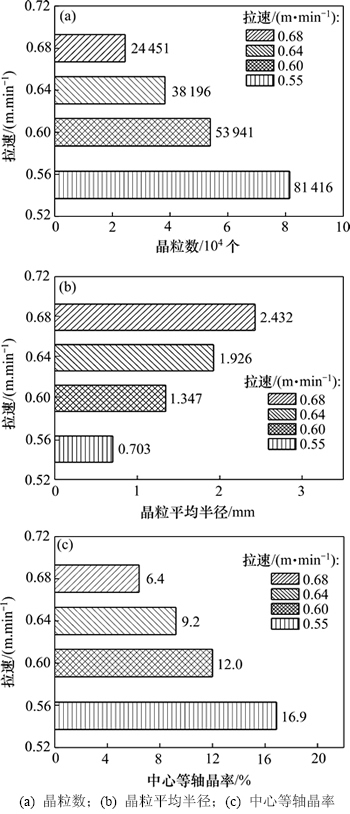
图7 不同拉速条件下的模拟统计结果
Fig.7 Simulated statistical results at different casting speeds
2.4 连铸工艺参数的优化
实际生产中,当钢水过热度过大或铸坯拉速过快时,会使形成的凝固坯壳偏薄,这将导致铸坯表面出现裂纹,甚至诱发拉漏事故;过热度过小,则在中间包中易形成高熔点的夹杂物,使水口发生堵塞;拉速太慢,不仅影响连铸操作,而且降低生产效率,在现场生产中不可行。因此,这2个参数的选择还需根据现场的生产实际来确定。
基于对模拟结果的统计分析,并结合现场的生产实际,最终选取钢水过热度为25 ℃,铸坯拉速为0.56 m/min,模拟结果和优化后的试验铸坯凝固组织如图8所示,优化前后的统计数据对比见表4。
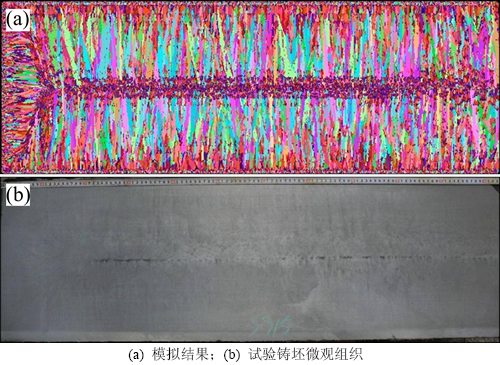
图8 优化后模拟结果和试验铸坯微观组织对比
Fig. 8 Comparison between simulation and experimental results after optimization
表4 优化前后的模拟统计结果对比
Table 4 Comparison of simulated statistical results between before and after optimization
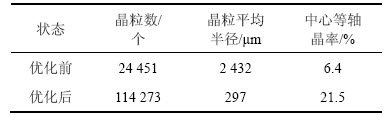
由表4可以看出:优化后的Q345B钢凝固组织中晶粒数明显增多,由原来的24 451个提高到114 273个,增长率达到367.4%;中心等轴晶率由6.4%增加到了21.5%,晶粒的平均半径也由2 432 μm减小到了297 μm。将优化后的连铸工艺参数应用到生产实际后,铸坯凝固组织如图8(b)所示。由图8(b)可以看出:中心等轴晶区在断面凝固组织中所占比例明显增大,柱状晶区比例有所减小,凝固组织结构较为理想,铸坯的中心偏析情况得到了明显改善。
3 结论
1) 运用二维切片法对Q345B宽厚板坯断面的温度场进行数值模拟,在此基础上利用CAFE模型对断面微观组织进行计算,得到的模拟结果与试验铸坯微观组织形貌基本一致。
2) 通过采用ProCAST软件模拟凝固组织晶粒度,Image Pro-Plus软件计算中心等轴晶率的方法,研究钢水过热度和铸坯拉速对铸坯断面凝固组织结构的影响。降低过热度或拉速均能增加断面中心等轴晶率和晶粒数,减小晶粒平均半径。
3) 在保证水口不堵塞,不影响生产效率的前提下,将过热度由34 ℃降低至25 ℃,拉速由0.68 m/min调整到0.56 m/min后,Q345B钢凝固组织中晶粒数增加367.4%,晶粒平均半径减小2 135 μm,中心等轴晶率也增加15.1%,铸坯中心偏析缺陷得到了有效改善。
参考文献:
[1] 常桂华, 吕志升, 修国涛, 等. 含铌、钒、钛微合金化钢连铸坯中心偏析影响因素及控制措施[J]. 钢铁, 2006, 41(2): 58-63.
CHANG Guihua, L Zhisheng, XIU Guotao, et al. Influencing factors in center segregation in continuously cast slab of Nb-V-Ti-contained micro-alloying steel and its control measures[J]. Iron and Steel, 2006, 41(2): 58-63.
Zhisheng, XIU Guotao, et al. Influencing factors in center segregation in continuously cast slab of Nb-V-Ti-contained micro-alloying steel and its control measures[J]. Iron and Steel, 2006, 41(2): 58-63.
[2] 赖朝彬, 辛博, 陈伟庆, 等. 连铸板坯二次枝晶臂间距对中心碳偏析的影响[J]. 炼钢, 2009, 25(4): 42-45.
LAI Chaobin, XIN Bo, CHEN Weiqing, et al. Effect of secondary dendritic spacing on center carbon segregation of slab[J]. Steelmaking, 2009, 25(4): 42-45.
[3] Rappaz M, Gandin Ch A. Probabilistic modelling of microstructure formation in solidification processes[J]. Acta Metallurgica et Materialia, 1993, 41(2): 345-351.
[4] Nastac L, Stefanescu D M. Stochastic modelling of microstructure formation in solidification processes[J]. Modelling and Simulation in Materials Science and Engineering, 1997, 5(4): 391-420.
[5] Zhu M F, Kim J M, Hong C P. A modified cellular automaton model for the simulation of dendritic growth in solidification of alloy[J]. ISIJ International, 2001, 41(5): 436-445.
[6] Zhu M F, Hong C P. Modeling of globular and dendritic structure evolution in solidification of an alloy 27wt% Si alloy[J]. ISIJ International, 2001, 41(9): 992-998.
[7] WANG Jinlong, WANG Fuming, LI Changrong, et al. Simulation of 3D-microstructure in free-cutting steel 9SMn28 under water cooling condition with convection and porosity[J]. ISIJ International, 2010, 50(2): 222-227.
[8] WANG Jinlong, WANG Fuming, LI Changrong, et al. Simulation of solidification microstructure and columnar to equiaxed transition in free-cutting steel 9SMn28 based on a CAF method[J]. Steel Research International, 2010, 81(2): 150-156.
method[J]. Steel Research International, 2010, 81(2): 150-156.
[9] WANG Jinlong, WANG Fuming, ZHAO Yanyu, et al. Numerical simulation of 3D-microstructure in solidification processes based on a CAF method[J]. International Journal of Minerals, Metallurgy and Materials, 2009, 16(6): 640-647.
method[J]. International Journal of Minerals, Metallurgy and Materials, 2009, 16(6): 640-647.
[10] 白李国, 刘海英, 张延玲, 等. 对22CrMoH连铸坯微观组织及合金元素影响的数值模拟[J]. 北京科技大学学报, 2011, 36(9): 1091-1098.
BAI Liguo, LIU Haiying, ZHANG Yanling, et al. Numerical simulation of the microstructure of 22CrMoH billets and the effects of alloying elements[J]. Journal of University of Science and Technology Beijing, 2011, 36(9): 1091-1098.
[11] Stefanescu D M, Kanetkar C S. Molding microstructural evolution of eutectic cast iron and of the gray/white transition (Retroactive coverage)[J]. Transactions of the American Foundry Society, 1987, 95: 139-144.
[12] Thevoz P H, Desbilles J L, Rappaz M. Modeling of equiaxed microstructure formation in casting[J]. Metallurgical Transactions A, 1989, 20(2): 311-322.
[13] 耿明山, 周守航, 韩庆礼, 等. 连铸圆坯凝固微观组织数值模拟[J]. 连铸, 2012(4): 10-14.
GENG Mingshan, ZHOU Shouhang, HAN Qingli, et al. Numerical simulation of solidification microstructure during continuous casting round bloom[J]. Continuous Casting, 2012(4): 10-14.
[14] 陈光友. Al-Si合金凝固组织的数值模拟[D]. 武汉: 武汉科技大学材料与冶金学院, 2009: 23-26.
CHEN Guangyou. Numerical simulation of solidification structure of Al-Si alloy[D]. Wuhan: Wuhan University of Science and Technology. School of Materials and Metallurgy, 2009: 23-26.
[15] Ignaszak Z, Hajkowski M, Hajkowski J. Prediction of dendritic microstructure using the cellular automaton-finite element method for hypoeutectic Al-Si alloys castings[J]. Journal of Materials Science, 2006, 12(2): 124-131.
[16] Gandin Ch A, Rappaz M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes[J]. Acta Metallurgica, 1994, 42 (7): 2233-2239.
[17] Gandin Ch A, Rappaz M. A 3D cellular automaton algorithm for the prediction of dendritic grain growth[J]. Acta Materialia, 1997, 45(5): 2187-2194.
[18] Kurz W, Giovanola B, Trivedi R. Theory of microstructural development during rapid solidification[J]. Acta Metallurgica et Materialia, 1986, 34(5): 823-829.
[19] Gandin Ch A, Desbiolles J L, Rappaz M, et al. A three-dimensional cellular automaton finite element model for the prediction of solidification grain structures[J]. Metallurgy and Materials Transactions A, 1999, 30(12): 3153-3160.
[20] 田陆, 包燕平, 黄郁君. 凝固组织对连铸板坯中心偏析的影响[J]. 北京科技大学学报, 2009, 34(增刊1): 164-167.
TIAN Lu, BAO Yanping, HUANG Yujun. Effect of solidification structures on the central segregation of slabs[J]. Journal of University of Science and Technology Beijing, 2009, 31(Suppl 1): 164-167.
(编辑 杨幼平)
收稿日期:2014-11-05;修回日期:2015-03-12
基金项目(Foundation item):国家自然科学基金资助项目(51374021) (Project(51374021) supported by the National Natural Science Foundation of China)
通信作者:杨树峰,博士,副教授,从事钢铁材料冶炼、连铸/铸造工艺与理论方面研究;E-mail: yangshufeng@ustb.edu.cn