DOI: 10.11817/j.issn.1672-7207.2019.08.023
深埋隧洞三岔口围岩稳定性计算理论
饶军应,谢财进,赵霞,刘灯凯,聂崇欣,刘宁
(贵州大学 土木工程学院,贵州 贵阳,550025)
摘要:为研究辅洞与隧洞主洞相交的三岔口区围岩稳定性,基于弹塑性理论圆形孔口应力计算方法,推导出深埋隧洞三岔口围岩稳定性计算理论。研究结果表明:当辅洞与隧洞主洞夹角( )为90°时,三岔口区围岩垂直应力σh达最大值,且σh随α和侧压力系数λ减小而减小;随着塑性圈半径R0减小,σh逐渐增大;由三岔口围岩到深部围岩,其应力集中系数K呈下降趋势;随着α增大,K也逐渐增大,直至α=90°时,K达到最大值;随着围岩等级降低,破坏深度Q逐渐增加,Ⅰ~Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度呈指数形式增加;当α一定时,理论最大等效跨度Ltmax仅与隧洞尺寸有关,极限等效跨度Lpmax还与Q有关;通过理论计算划定辅洞修建跨度的安全范围与极限范围。
)为90°时,三岔口区围岩垂直应力σh达最大值,且σh随α和侧压力系数λ减小而减小;随着塑性圈半径R0减小,σh逐渐增大;由三岔口围岩到深部围岩,其应力集中系数K呈下降趋势;随着α增大,K也逐渐增大,直至α=90°时,K达到最大值;随着围岩等级降低,破坏深度Q逐渐增加,Ⅰ~Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度呈指数形式增加;当α一定时,理论最大等效跨度Ltmax仅与隧洞尺寸有关,极限等效跨度Lpmax还与Q有关;通过理论计算划定辅洞修建跨度的安全范围与极限范围。
关键词:深埋隧洞;三岔口;围岩应力;弹塑性理论;圆形孔口应力
中图分类号:U45+.2 文献标志码:A 文章编号:1672-7207(2019)08-1949-11
Theoretical stability calculation of surrounding rocks in divergence of deep tunnel
RAO Junying, XIE Caijin, ZHAO Xia, LIU Dengkai, NIE Chongxin, LIU Ning
(School of Civil Engineering, Guizhou University, Guiyang 550025, China)
Abstract: In order to study the stability of the surrounding rock in the divergence area, based on elastoplastic theory, the calculation theory of the surrounding rock stability of the divergence deep tunnel was derived. The results show when the hole angle (α) of auxiliary tunnel and tunnel main is 90 °, the vertical stress σh of the surrounding rock in divergence reaches the maximum value, and σh decreases with the decrease of α and side pressure coefficient λ. As the circle radius R0 decreases, σh increases gradually. The stress concentration factor K decreases from the surrounding rock of divergence to the deep surrounding rock. As α increases, K also increases. When α is 90°, K reaches the maximum value. As the surrounding rock grade decreases, the depth of failure Q increases gradually. The depth of damage of the I~IV surrounding rock triangle is not obvious. The depth of damage in the V-class surrounding rock increases exponentially. When α is constant, the theoretical maximum equivalent span Ltmax is only related to the tunnel size. The limit equivalent span Lpmax is also related to Q, and the safe range and limit range of the auxiliary tunnel construction span are delineated by theoretical calculation.
Key words: deep tunnel; divergence; surrounding rock stress; elastoplastic theory; circular orifice stress
随着我国交通行业飞速发展,隧洞建设规模越来越大,隧洞也越修越长,对技术的要求越来越高。为满足隧洞工期及运营通风需求,需要增设斜井、横通道等辅助坑道,而辅洞与主洞连接处会形成三岔口。从力学角度分析,隧洞主洞的围岩受力通常可视为平面进行求解,当存在辅助坑道介入主洞时,三岔口区的围岩受力将变得十分复杂,该区域内的开挖易造成隧洞围岩的受力状态由最初的三向受力转变为开挖后的单向或二向受力,且应力分布也截然不同,若未探明三岔口区围岩应力的分布情况,贸然掘进会增加施工风险。三岔口区围岩极易松动、掉块或坍塌,是隧洞开挖时的薄弱点,需予以特别关注,为此,有必要研究三岔口处围岩受力分布[1-3]。近年来,学者们就隧洞三岔口处围岩稳定性开展大量研究,基于已有文献可知,主要有数值分析和应用研究2个大类[4-12]。在数值分析方面,罗彦斌等[13]通过现场实测和有限元数值模拟,研究了横通道斜交隧洞对主隧洞结构受力及变形的影响,但未涉及理论解析;蔺云红等[14]研究了地铁暗挖隧洞斜交下穿既有铁路工程时的地层沉降和塑性区分布,仍依靠数值模拟分析,未涉及理论解析。在应用研究方面,李东海等[15]结合工程实例,对盾构隧洞斜交下穿地铁车站的施工进行了分析,仅依靠监测数据和工程经验给出施工指导意见,未给出理论解释。已有研究成果表明:新建隧洞三岔口区设计、施工的主要依据源于类似工程的数值模拟、施工参数及工程经验,在理论解析层面还有待加深。本文基于辅助坑道连接隧洞主洞,对其三岔口区围岩稳定性进行理论探讨,以便为类似工程的设计、施工提供理论支撑。

图1 隧洞三岔口受力计算分析图
Fig.1 Analysis of force calculation of the tunnel three mouths

图2 隧洞围岩应力分布范围及计算简图
Fig. 2 Stress distribution range and calculation sketch of tunnel surrounding rock
1 隧洞三岔口围岩应力分析
隧洞开挖后,围岩应力将重新分布,局部可能出现应力集中,导致变形甚至失稳破坏。图1所示为隧洞三岔口受力计算分析图。分析图1可知:辅洞与隧洞主洞相交成锐角一侧(定义为三角区)受力面积小,该区域受应力集中破坏可能性最大。为计算简便,假设隧洞主洞、辅洞为不同直径的圆形隧洞,且为深埋隧洞(围岩应力计算时仅考虑岩体容重与隧道埋深),此时,隧洞边界岩体所受应力简化为垂直应力P( ,γ为岩体容重,H为隧洞埋深)和水平应力q(
,γ为岩体容重,H为隧洞埋深)和水平应力q( ,λ是侧压力系数),忽略围岩自重的影响。
,λ是侧压力系数),忽略围岩自重的影响。
按弹性理论中的基尔希公式建立如图2所示的计算模型,计算围岩中任一点Q(ρ,θ)的应力[16]:



 (1)
(1)


 (2)
(2)

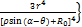 (3)
(3)
式中:σρ为沿ρ方向的正应力;σθ为沿θ方向的正应力;τρθ为切应力;R0为隧洞三岔口中心至塑性变形圈边界的距离;r为隧洞主洞开挖半径;ρ和θ为某点应力的极坐标;α为辅洞与隧洞主洞的交叉角度(锐角)。
根据隧洞三角区域围岩力学特征及圆形隧洞弹性状态下围岩应力计算公式[17],可得隧洞三角区围岩垂直应力σh为

 (4)
(4)
式中:σ1和σ2分别为原岩垂直应力和水平应力,且σ1=P,σ2=q=λP。
将σ1和σ2代入式(4),可得

 (5)
(5)
简化为


 (6)
(6)
要计算σh,还需求解未知量R0,由卡斯特纳(Kastner)公式得:
 (7)
(7)
式中:ξ为摩尔圆强度线的斜率;σc为岩石抗压强度。
由摩尔-库仑强度理论得:
 (8)
(8)
经简化得
 (9)
(9)
由于 ,可得:
,可得: ;
; (其中:c和
(其中:c和 分别为岩体粘聚力和内摩擦角)。
分别为岩体粘聚力和内摩擦角)。
将σc代入式(7)得
 (10)
(10)
随着隧洞的开挖,其三角区围岩应力将重新分布,并伴随应力集中现象的产生,该区域应力集中的强弱用系数K表示。

 (11)
(11)
由式(11)可知,三角区围岩应力与原岩应力、围岩自身强度、岩体侧压力系数、隧洞截面形状、尺寸及辅洞与隧洞主洞的交叉角度有关。
2 三岔口围岩破坏规律分析
2.1 三岔口围岩破坏深度分析
图3所示为围岩状态分布图。隧洞三角区围岩应力集中系数较高,当集中应力大于岩体极限屈服强度时,围岩由于支撑力不足发生塑性屈服破坏。随破坏区的扩散,围岩周围将依次形成松动区、破碎区、破裂区、塑性区、弹性区和原岩区。图4所示为弹塑性区围岩应力分布特征图。由图4可见:若集中应力未超过岩体极限屈服强度,可认为围岩处于极限应力平衡状态。根据弹塑性区围岩应力分布,由弹塑性极限平衡理论可知:

图3 围岩状态分布图
Fig.3 Distribution of surrounding rock state

图4 弹塑性区围岩应力分布特征图
Fig.4 Stress distribution of surrounding rock in elastoplastic zone
弹性区围岩应力可描述为[18-19]:
 (12)
(12)
式中:σre为弹性区径向应力;σθe为弹性区环向应力;r1为松动圈半径, ;P1为支架反力。
;P1为支架反力。
结合式(12),可知三角区应力叠加后弹性区内沿水平方向的铅垂应力σx和沿铅垂方向的水平应力σy为:
 (13)
(13)
式中:x和y为辅洞与主洞的掘进距离; r 为斜井开挖半径。
为斜井开挖半径。
塑性区围岩应力可描述为[18-19]:
 (14)
(14)
式中:σrP为塑性区径向应力;σθP为塑性区环向应力。
结合式(14),可知三角区应力叠加后塑性区内沿水平方向的铅垂应力σx和沿铅垂方向的水平应力σy为:
 (15)
(15)
联立式(13)和(15)解得三角区围岩水平方向和铅垂方向的破坏深度为:
 (16)
(16)
式中:Xmax和Ymax分别为三角区围岩水平方向和铅垂方向的破坏深度。
图5所示为三角区围岩应力分布及破坏范围分布图。由图5可见:沿x方向的三角区最大破坏深度为Xmax,沿y方向的三角区最大破坏深度为Ymax。

图5 三角区围岩应力分布及破坏范围分布图
Fig. 5 Stress distribution and damage range of surrounding rock in triangle area
水平方向铅垂应力的峰值位于x=Xmax处,为P3;铅垂方向水平应力的峰值位于y=Ymax处,为P2。2条应力曲线的交汇处围岩应力集中系数最大,由数学关系可知围岩最大破坏深度Q为
 (17)
(17)
将式(16)代入式(17)得:

 (18)
(18)
由于应力叠加的作用导致三岔口处形成曲边三角形破坏区,其最大破坏深度与隧洞、辅洞开挖尺寸、原岩应力、岩体自身强度以及辅洞与主洞交角有关。若辅洞进主洞的开挖过度曲线在破坏区域内,则三岔口区围岩不稳定,需进行加固;反之,三岔口区围岩稳定。
2.2 三岔口围岩等效跨度分析
图6所示为围岩压力变化特征曲线。由图6可见:根据围岩变形特征分为弹塑性阶段(AB段)、小松动变形阶段(BC段)、大松动变形阶段(CD段)。隧洞三岔口围岩由于二次开挖导致应力集中,当集中应力大于围岩极限强度时,围岩将发生塑性屈服破坏,失去支承能力。在无支护条件下,隧洞顶板将会进入小变形阶段甚至大变形失稳破坏阶段,主要表现在较软弱岩层中顶板冒落及隧洞两帮支撑力不足时顶板弯曲下沉[20-24]。

图6 围岩压力变化特征曲线
Fig.6 Curve of variation of surrounding rock pressure
图7所示为隧洞三岔口区跨度示意图。由图7可见:顶板弯曲下沉时,基于隧洞三岔口围岩破坏形式及特征,采用等效跨度理论计算该区域理论最大等效跨度Ltmax和极限等效跨度Lpmax[25]。

图7 隧洞三岔口区跨度示意图
Fig.7 Schematic diagram of span of the tunnel
由隧洞三岔口处的几何关系可得
 (19)
(19)
 (20)
(20)
将式(18)代入式(20)可得:

 (21)
(21)
等效跨度值作为隧洞三岔口区围岩变形位移参数,可反映围岩稳定性。该值不仅受交叉角α、隧洞尺寸r和r 及破坏深度Q的影响,而且与隧洞埋深H、围岩力学参数等有关。通过研究发现:当实际修建跨度值L不大于Ltmax时,即L≤Ltmax,三角区围岩稳定;当遇特殊地质条件时,L会超出Ltmax,但不大于Ltmax,即Ltmax≤L ≤Lpmax,此时,需对三角区围岩进行适当加固;若L≥Lpmax,则三角区围岩极不稳定,需采取有效加固措施。
及破坏深度Q的影响,而且与隧洞埋深H、围岩力学参数等有关。通过研究发现:当实际修建跨度值L不大于Ltmax时,即L≤Ltmax,三角区围岩稳定;当遇特殊地质条件时,L会超出Ltmax,但不大于Ltmax,即Ltmax≤L ≤Lpmax,此时,需对三角区围岩进行适当加固;若L≥Lpmax,则三角区围岩极不稳定,需采取有效加固措施。
3 算例与分析
以贵阳市轨道交通2号线区间为例,全区间采用矿山法,隧洞为双洞单线马蹄形断面结构,采用复合式衬砌,最大埋深53.2 m。为计算简便,取岩体容重γ=19 kN/m3,隧洞埋深H=50 m,将该隧洞主洞、辅洞分别假定为半径r=5.0 m, m的圆形隧洞。
m的圆形隧洞。
3.1 隧洞三角区垂直应力分析
1) 当R0→∞,得
 (22)
(22)
隧洞三角区围岩垂直应力仅与隧洞上部岩体容重及隧洞埋深有关。
2) 当R0为5r,4r,3r和2r时,分别得式(23),(24),(25)和(26):


 (23)
(23)

 (24)
(24)

 (25)
(25)

 (26)
(26)
取侧压力系数λ=0.5,α分别为30°,45°,60°和90°时,由式(22)~(26)分别得σh的分布曲线。图8所示为不同塑性圈下三角区垂直应力分布图。由图8可见:随着X逐渐减小,围岩所受垂直应力也逐渐减小;随着α逐渐减小,三角区两侧的围岩应力差值变小,隧道结构更稳定;当α=30°时,三角区所受峰值应力最小,且两侧围岩垂直应力差值最小,三角区围岩较为稳定,开挖条件较好;当α=90°时,三角区所受峰值应力最大,且两侧围岩垂直应力差值最大,三角区围岩极不稳定,此种开挖方案安全风险极高;随着R0减小,σh逐渐增大,且三角区两侧σh差值逐渐增大,不利于隧道稳定。故需通过围岩力学参数确定塑性圈范围,根据垂直应力对隧洞三岔口区进行合理加固与开挖。

图8 不同R0下三角区垂直应力分布
Fig.8 Vertical stress distribution of lower triangular region in different R0
取R0=3r,当λ为0.2,0.4,0.6,0.8和1.0时,不同α下σh分布曲线如图9所示。从图9可见:随着α增大,三角区两侧围岩应力差值变大,隧道围岩不稳定;当α=90°时,围岩垂直应力最大,随着α和λ减小,σh都减小。根据地勘参数及围岩力学参数,可计算不同围岩级别下隧洞周围的水平应力及垂直应力,并根据垂直应力值对隧洞三岔口区进行合理加固。

图9 不同α下三角区垂直应力分布图
Fig. 9 Vertical stress distribution in different α lower triangular region
为进一步验证本文理论解析的可行性,现用ANSYS有限元软件对辅洞与主洞交叉角呈45°时的算例进行数值模拟计算,其网格划分如图10所示。

图10 ANSYS有限元计算网格划分图
Fig. 10 ANSYS finite element calculation grid division diagram
取α=45°,λ=0.5,三岔口区处于Ⅲ级围岩中,数值模拟结果、解析计算结果如表1所示。由表1可见:1) 解析计算和数值计算三岔口区围岩垂直应力最大值间存在的最大误差仅为3.92%;2) 在同种工况下2种计算方法的结果存在微小误差,原因在于理论解计算结果为确定值,而数值解则是近似运算的结果,且2种方法的计算假定条件存在差异;3) 理论解与数值解间的计算结果十分接近,验证了本文解析法在三岔口区围岩稳定性计算中的可行性和准确性。
3.2 隧洞三角区应力集中分析
图11所示为三岔口应力集中系数等值线分布图。由图11可见:越靠近围岩三岔口交叉点,围岩应力集中系数越大,三角区域最外围的应力集中系数最小。这是由于隧洞开挖过程中三角区域外围岩体容易破坏,在其表面形成卸压区,为给横通道与主洞交叉处的顶板提供足够支撑力,有效支撑区将会向岩体深部转移,故而应力集中减弱。在实际工程中,一般会将辅洞与隧洞主洞交叉处的尖角部分去掉修建成曲线状,该过渡曲线应不越过K等值曲线,且与其弯曲程度相似,最好与等值曲线重合。
由式(11)可知:影响应力集中系数的主要因素有λ,r,R0及α。其中λ和R0是由隧洞所处地理位置决定,针对不同用途r也有相应固定标准,在实际工程中,α的随机性较大。
当λ取0.5,R0取3r,r取5 m,代入式(11)后得:


 (27)
(27)
由式(27)绘制不同α下的K曲线,如图12所示。由图12可见:随着α的增大,K的峰值逐渐变大,当α=90°时,K的峰值最大。此时三角区应力高度集中,围岩稳定性差,不宜于开挖。故而辅助坑道进入隧洞时需以一定角度进入,避免正交方式。

图11 三岔口应力集中系数等值线分布图
Fig. 11 Contour map of stress concentration factor of divergence

图12 应力集中系数曲线图
Fig. 12 Curves of stress concentration factor
表1 辅洞与主洞夹角为45°三岔口区围岩垂直应力最大值
Table 1 Maximum value of vertical stress of surrounding rock in divergence area when the angle between the auxiliary hole and the main hole is 45°/MPa

3.3 隧洞三角区破坏深度分析
表2所示为不同围岩级别下摩擦角φ和黏聚力c。随着围岩等级降低,岩体摩擦角φ和黏聚力c逐渐减小。不同等级围岩过渡转换时,可根据隧洞三角区最大破坏深度理论计算值,对其加固进行合理化建议。
表2 不同围岩级别下c和
Table 2 c and φ values under different surrounding rock levels

由式(18)可计算不同围岩级别下隧洞三角区最大破坏深度。图13所示为围岩破坏深度曲线图。由图13可见:随着围岩等级降低,破坏深度逐渐增加,Ⅰ至Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度层指数形式增加,围岩级别越差,三角区破坏深度越深。另外,在围岩等级过渡段,其破坏深度会发生突变,故在围岩不均匀地段开挖时,需考虑应力突变的状况;在围岩过渡段设计、施工时,需设置一定的安全系数。

图13 围岩破坏深度曲线图
Fig. 13 Surrounding rock failure depth curve
3.4 隧洞三角区等效跨度分析
图14(a)所示是由式(19)绘制的α与Ltmax的关系曲线。由图14(a)可见:随α增大,Ltmax单调递增,当α=90°时,Ltmax达到最大值,Ltmax曲线下方为隧洞开挖安全区。
令最大破坏深度Q=5 m,图14(b)所示是由式(20)绘制的α与Lpmax关系曲线。由图14(b)可见:随α增大,Lpmax单调递增,当α=90°时,Lpmax达到最大值。当遇特殊情况时,开挖等效跨度可适当增加,但也不能超过Lpmax曲线的范围。Ltmax曲线下方为开挖安全区,Lpmax曲线与Ltmax曲线之间为开挖极限区。

图14 交叉角(α)与等效跨度的关系曲线
Fig.14 Cross angle (α) and equivalent span relationship curve
当辅洞与隧洞主洞交角α=90°时,得:
 (28)
(28)
 (29)
(29)
将式(18)代入式(29)得:
 (30)
(30)
由式(19)和(20)可知,当辅洞与隧洞主洞交角一定时,理论最大等效跨度仅与隧洞尺寸有关,极限等效跨度还与最大破坏深度有关。在设计辅洞进入主洞区时,实际修建跨度应小于理论最大等效跨度,在特殊条件下也不能大于极限等效跨度。
4 结论
1) 当α=90°时,围岩垂直应力最大,随着α和λ减小,σh减小;随着R0减小,σh逐渐增大。已知围岩力学参数、地勘参数,就可根据理论公式对隧洞三岔口区围岩进行合理加固。
2) 在隧洞开挖过程中,越靠近围岩三岔口的交叉点K越大,三角区域最外围的K最小,且随着α的增大,K逐渐变大,当α=90°时,K达到最大值。
3) 随着围岩等级的降低,破坏深度越大,Ⅰ~Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度呈指数形式增加。
4) 隧洞三角区的集中应力大于围岩极限强度时,围岩会发生塑性屈服破坏,失去支承能力,在无支护条件下隧洞顶板将会进入小变形阶段,甚至进入大变形失稳破坏阶段。
5) 当α一定时,Ltmax仅与隧洞尺寸有关,Lpmax还与最大破坏深度有关。在设计辅洞进入主洞区时,L应小于Ltmax,在特殊条件下也不能大于Lpmax。
参考文献:
[1] 刘京强, 都锋. 交叉角度对巷道三岔口围岩稳定性的影响[J]. 煤矿安全, 2015, 46(7): 200-203.
LIU Jingqiang, DU Feng. Effect of crossing angles on stability of roadway divergence[J]. Safety in Coal Mines, 2015, 46(7): 200-203.
[2] 张伟, 孙龙华. 巷道交叉角度对围岩稳定性影响分析研究[J]. 煤炭工程, 2014, 46(12): 101-104.
ZHANG Wei, SUN Longhua. Study on analysis on cross angle of mine roadway affected to stability of surrounding rock[J]. Coal Engineering, 2014, 46(12): 101-104.
[3] 曾新发, 彭振斌, 何杰, 等. 地下洞室开挖围岩弹塑性动态稳定性分析[J]. 中南大学学报(自然科学版), 2014, 45(4): 1293-1301.
ZENG Xinfa, PENG Zhenbin, HE Jie, et al. Elasto-plastic dynamic stability of surrounding rock during excavation of underground cavern[J]. Journal of Central South University(Science and Technology), 2014, 45(4): 1293-1301.
[4] 范永慧, 戴俊, 王志远. 偏压隧道斜交进洞法及其三维数值模拟研究[J]. 公路, 2015, 60(2): 230-235.
FAN Yonghui, DAI Jun, WANG Zhiyuan. Study of skew bias tunnel crossing method and three-dimensional numerical simulation[J]. Highway, 2015, 60(2): 230-235.
[5] 关玲. 不同的开挖方式对公路隧道围岩稳定性影响分析: 以重庆公路隧道为例[J]. 公路工程, 2019, 44(1): 156-160.
GUAN Ling. Influence of different excavation methods on stability of surrounding rock of highway tunnel: taking chongqing highway tunnel as an example[J]. Highway Engineering, 2019, 44(1): 156-160.
[6] 庄乐. 隧道过渡段开挖过程的数值模拟及研究[D].中南大学土木工程学院, 2014: 1-27.
Zhuang Le. Numerical simulation and research on the excavation process of tunnel transition section[D]. Changsha: School of Civil Engineering, Central South University,2014: 1-27.
[7] 张顶立, 孙振宇, 侯艳娟. 隧道支护结构体系及其协同作用[J]. 力学学报, 2019, 51(2): 577-593.
ZHANG Dingli, SUN Zhenyu, HOU Yanjuan. Tunnel support structure system and its synergistic effect[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 577-593.
[8] LI Jinkui, WEI Xianke, LIANG Wenjing. The effects of different excavation angle on intersecting tunnel surrounding rock stability[C]//Proceedings of the 2nd International Conference on Modelling, Identification and Control. Paris, France: Atlantis Press, 2015: 290-293.
[9] 高虎艳, 黄强兵, 王德志, 等. 西安地铁三号线隧道斜交穿越地裂缝带的设防参数研究[J]. 现代隧道技术, 2012, 49(6): 128-132, 146.
GAO Huyan, HUANG Qiangbing, WANG Dezhi, et al. A study of design parameters for the tunnels of the Xi'an metro line 3 passing obliquely through active ground fissure zones[J]. Modern Tunnelling Technology, 2012, 49(6): 128-132, 146.
[10] 李建军, 邵生俊, 熊田芳. 隧道斜交穿越地裂缝的模型试验研究[J]. 岩土力学, 2010, 31(S1): 115-120, 126.
LI Jianjun, SHAO Shengjun, XIONG Tianfang. Research on physical model experiment of tunnel obliquely crossing a ground fissure[J]. Rock and Soil Mechanics, 2010, 31(S1): 115-120, 126.
[11] 郭子红, 刘新荣, 舒志乐. 深埋隧道围岩滑移面验证及稳定性分析[J]. 中南大学学报(自然科学版), 2012, 43(1): 315-321.
GUO Zihong, LIU Xinrong, SHU Zhile. Verification of deep tunnel rock mass sliding surface and stability analysis[J]. Journal of Central South University(Science and Technology), 2012, 43(1): 315-321.
[12] ZHENG Yingren, QIU Chenyu, XIAO Qiang. Research on the stability analysis and design of soil tunnel surrounding rock[J]. Engineering Sciences, 2010, 28(3): 57-70.
[13] 罗彦斌, 陈建勋, 王梦恕. 隧道斜交横通道施工对主隧道衬砌结构的影响研究[J]. 岩石力学与工程学报, 2010, 29(S2): 3792-3798.
LUO Yanbin, CHEN Jianxun, WANG Mengshu. Study of influence of skew horizontal adit tunnel construction on main tunnel lining structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3792-3798.
[14] 蔺云宏, 李冀伟, 王飞. 暗挖地铁隧道斜交下穿既有铁路的施工研究[J]. 铁道工程学报, 2012, 29(11): 82-86.
LIN Yunhong, LI Yiwei, WANG Fei. Study on construction of subsurface excavated metro tunnel under-passing existing railway[J]. Journal of Railway Engineering Society, 2012, 29(11): 82-86.
[15] 李东海, 刘军, 萧岩, 等. 盾构隧道斜交下穿地铁车站的影响与监测研究[J]. 岩石力学与工程学报, 2009, 28(S1): 3186-3192.
LI Donghai, LIU Jun, XIAO Yan, et al. Research on influence and monitoring of shield tunnel obliquely crossing beneath existing subway station[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 3186-3192.
[16] 孙龙华. 巷道三岔口围岩稳定性特征及控制方法研究[D].太原理工大学矿业工程学院,2014:13-22.
Sun Longhua. Study on the surrounding rock stability characteristics and control method in the roadway junction[D]. School of Mining Engineering, Taiyuan University of Technology,2014:13-22.
[17] YU Yang, BAI Jianbiao, CHEN Ke, et al. Failure mechanism and stability control technology of rock surrounding a roadway in complex stress conditions[J]. Mining Science and Technology (China), 2011, 21(3): 301-306.
[18] 周恒, 漆泰岳, 于加云. 深部极软岩巷道补充锚注加固机理及应用[J]. 现代隧道技术, 2006, 43(5): 55-59.
ZHOU Heng, QI Taiyue, YU Jiayun. Mechanism and application of the supplementary bolt-grouting strengthening for a gallery embedded in deep soft rock[J]. Modern Tunnelling Technology, 2006, 43(5): 55-59.
[19] 宋宏伟, 王闯, 贾颖绚. 用地质雷达测试围岩松动圈的原理与实践[J]. 中国矿业大学学报, 2002, 31(4): 370-373.
SONG Hongwei, WANG Chuang, JIA Yingxuan. Principle of measuring broken rock zone around underground roadway with GPR and its application[J]. Journal of China University of Mining & Technology, 2002, 31(4): 370-373.
[20] 马睿. 巷道快速掘进空顶区顶板破坏机理及稳定性控制[D]. 徐州:中国矿业大学矿业工程学院,2016:1-48.
Ma Rui. Failure mechanism and stability control of empty roof in roadway rapid excavation [D]. Xuzhou: School of Mining Engineering, China University of Mining and Technology,2016:1-48.
[21] 曾赤. 煤矿复合顶板巷道冒顶机理及防控研究[D]. 湘潭:湖南科技大学能源与安全工程学院,2015:49-59.
ZENG Chi. Research on mechanism and prevention and control of roof caving in composite roof roadway of coal mine [D]. Xiangtan, China: College of Energy and Security Engineering, Hunan University of Science and Technology,2015:49-59.
[22] JIANG Zhongan, CHEN Ya, TAN Cong. Study on prediction model of roof falling based on crisis signs in coal mine[C]//Proceedings of the 2015 International Conference on Industrial Technology and Management Science, 2015. Beijing, China. Paris, France: Atlantis Press, 2015: 260-264.
[23] 郭健, 阳军生, 陈维, 等. 基于现场实测的炭质板岩隧道围岩大变形与衬砌受力特征研究[J]. 岩石力学与工程学报, 2019, 38(4): 832-841.
GUO Jian, YANG Junsheng, CHEN Wei, et al. Research on large deformation of surrounding rock and mechanical characteristics of lining of carbonaceous slate tunnel based on field measurement[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(4): 832-841.
[24] 刘银涛, 李治国, 种玉配, 等. 深埋碳质板岩隧道采用不同开挖方法时围岩及初期支护变形特征[J]. 铁道建筑, 2019(2): 81-84.
LIU Yintao, LI Zhiguo, ZHONG Yupei, et al. Deformation features of surrounding rock and primary support for tunnel in deep buried carbonaceous slate with different excavation methods[J]. Railway Engineering, 2019(2): 81-84.
[25] 平寿康, 刘明. 交叉点围岩稳定性分析—巷道顶板事故机理研究[J]. 矿山压力与顶板管理,1990, 1(1): 33-39.
PING Shoukang, LIU Ming. Stability analysis of surrounding rock at intersection—study on roadway roof accident mechanism [J]. Mine pressure and roof management, 1990, 1(1): 33-39.
(编辑 秦明阳)
收稿日期: 2019 -03 -12; 修回日期: 2019 -05 -20
基金项目(Foundation item):国家自然科学基金资助项目(51608141);贵州省科技计划项目([2016]1041);贵州省土木工程一流学科(QYNYL[2017]0013)(Project(51608141) supported by the National Natural Science Foundation of China; Project([2016]1041)supported by Science and Technology Plan of Guizhou Province; Project(QYNYL[2017]0013) supported by the Guizhou Province Civil Engineering First Class)
通信作者:饶军应,博士,从事岩土、隧道工程科研工作;E-mail: jyrao@gzu.edu.cn