DOI: 10.11817/j.issn.1672-7207.2017.08.032
弯曲倾倒模式下薄层状反倾岩质边坡锚固力研究
高旭1,晏鄂川1,张世殊2,赵小平2,田雄2
(1. 中国地质大学 工程学院,湖北 武汉,430074;
2. 中国电建集团 成都勘测设计院有限公司,四川 成都,610072)
摘要:基于悬臂梁理论建立锚固力解析计算模型,以某薄层状反倾岩质边坡为实例,进行锚固力计算及相关参数敏感性分析,并以数值模拟加以对比分析。研究结果表明:此类边坡锚固力计算可划分为倾倒锚固区和滑动锚固区,其中倾倒锚固区折断深度和锚固力都随坡顶距增大而减小,且最大折断深度和最大锚固力对相关参数敏感性由大到小依次为:层厚、抗拉强度、层间内摩擦角。数值模拟中锚索轴力增量比随坡顶距增大而减小,与解析计算结果变化规律一致,且加固倾倒锚固区比加固滑动锚固区对于控制边坡水平位移效果更加明显。
关键词:反倾岩质边坡;弯曲倾倒模式;锚固力;解析解;数值模拟
中图分类号:TU45 文献标志码:A 文章编号:1672-7207(2017)10-2790-10
Research on anchorage force of a thin layered anti-dip rock slope under bending and toppling mode
GAO Xu1, YAN Echuan1, ZHANG Shishu2, ZHAO Xiaoping2, TIAN Xiong2
(1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China;
2. Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China)
Abstract: Based on the cantilever beam theory, an analytical model for calculating the anchorage force was proposed. A thin layered anti-dip rock slope was set as an example. The anchorage force was computed and the related parameter sensitivity was analyzed. The anchorage force yielded from the analytical model was compared with that of numerical simulation. The results show that there are toppling zone and sliding zone in the anchorage force calculation of this type of slope. With the increasing distance from the top of the slope in the toppling anchorage zone, the broken depth and anchorage force decrease. Their sensitivities to related parameters are shown as follows in descending order: layer thickness, tensile strength, internal friction angle. On the other hand, the anchorage forces produced from numerical simulation are consistent with the results of the analytical simulation. In terms of controlling the horizontal displacement of this slope, it would be better to anchor in toppling zone than doing it in sliding zone.
Key words: anti-dip rock slope; bending and toppling mode; anchorage force; analytical model;numerical simulation
反倾层状岩质边坡的变形破坏模式可分为块体倾倒和弯曲倾倒2类。纵观反倾边坡的研究历程,块体倾倒的极限平衡分析已较为成熟[1-7],工程处治也相对容易,而弯曲倾倒多发生在由塑性的薄层状岩层或软硬相间组成的反倾边坡中,这种边坡变形发展较慢,只有浅表层岩块脱落,边坡保持相对完整,目前仍无确定性方法预测这样一个边坡是会持续缓慢变形还是会转化为大规模破坏,因此,需要充分利用其岩体强度,提前进行锚固。锚固力及其安设部位要充分考虑边坡软弱结构面的产状及边坡可能发生的破坏模式,以便能最大限度提高抵抗滑移或倾倒破坏的抗力[8]。对于反倾层状岩质边坡的弯曲倾倒破坏模式,规范 SL 386—2007“水利水电工程边坡设计规范”建议锚固边坡中上部,以抵抗倾倒弯矩抗力为目的,但锚固计算仍选择以折断带为滑面的滑动计算模式,此锚固计算模式与锚固目的并不切合。张布荣[9]针对抚顺西露天矿反倾岩质边坡特点进行了边坡稳定性分析和加固机理的研究,提出了“串层锚杆”加固成层反倾岩质边坡,给出了串层锚杆的设计参数,该方法完全是从力学角度考虑,没有考虑施工可行性;SAGASETA等[10]以微分方程描述倾倒块体的平衡状态,提出了一般解析分析方法来求解边坡所需锚固力,对于岩块长细比为20~30时,能给出较为准确的计算结果,而对于长细比较小时,得到的结果与真实值之间有较大差异;LIU等[11-12]基于极限平衡理论,提出了岩质边坡块体倾倒破坏稳定的传递系数法,并采用了Excel进行了程序化分析;杨保军等[13]采用改进传递系数法提出了岩质边坡滑动-倾倒组合破坏的解析分析方法,确定整个坡体由滑动转为倾倒或由倾倒转为滑动的具体位置,并确定坡体需要的锚固力。以往关于反倾岩质边坡锚固力研究很少涉及到薄层状岩体,并且大都偏重于边坡稳定性分析,鲜有对薄层状反倾岩质边坡锚固力进行研究。本文作者在前人研究的基础上,基于悬臂梁理论建立锚固计算模型,并以雅鲁藏布江某水电站导流明渠边坡为实例,提出“等效层厚”概念概化薄层状反倾岩质边坡地质模型,进而开展锚固力计算和相关参数敏感性分析,最后进行边坡上部锚固和下部锚固2种工况下数值模拟,得出锚索轴力和边坡水平位移变化规律,并与前文解析计算结果进行比较分析。
1 建立锚固计算模型
水电工程中反倾边坡弯曲倾倒现象是漫长地质历史过程(河谷下切)的产物[14],板状岩体在自重弯矩作用下,向临空方向逐渐作悬臂梁弯曲,当变形发展到一定阶段,达到岩体极限强度发生折断并倾倒,即弯曲-折断-倾倒力学机制。刻画这一力学机制常用的有2种力学计算模型:叠合悬臂梁模型和独立悬臂梁模型[15]。两者相同点在于:假定各层面间的c和φ相同;岩体各向同性。两者不同点在于:叠合悬臂梁模型假定岩层受自重、岩层上下层面间的正、剪应力,且均匀分布(或三角形分布);独立悬臂梁模型假定各岩层变形折断前,任意岩层的下边界均有一瞬时临空状态,只受自重、上部岩层的重力以及层间摩擦力作用[1]。锚固力计算模型的选取既要反映地质体变形破坏的力学机制,同时工程设计应该相对保守,由于独立悬臂梁模型不考虑下部岩层对梁板抵抗力矩,需要更大锚固力以增加抵抗力矩,在暂不考虑工程设计经济性情况下,本文以独立悬臂梁模型为基础研究锚固计算模型。
1.1 简化应力状态合理性解释
为使解析计算成为可能,悬臂梁力学分析模型中都离不开对斜坡中一点处应力状态进行简化。文献[16-17]中将斜坡内部应力简化为垂直的自重应力和水平的侧压力2部分,在近似分析中直观简明,然而对其可行性并未作出合理解释,故本文假设边坡中任意点处主应力与同位置处自重应力变化规律一致,基于Geo-Studio软件SIGMA/W模块进行数值试验,探索不同坡比下边坡任意点处最大主应力(σ1)变化规律,以佐证文献[16-17]中应力简化状态的合理性。图1所示为数值试验模型示意图。图中:H为距坡顶距离;n为坡比;E为弹性模量;μ为泊松比。设计坡比为1:n,改变n以监测距离坡顶H四点各处主应力,当n=∞时,即为理想情况下应力状态(垂直的自重应力和水平的侧压力),其中模型左右边界约束水平位移,底边界约束垂直位移,采用线弹性模型,将监测值绘于图2和图3。
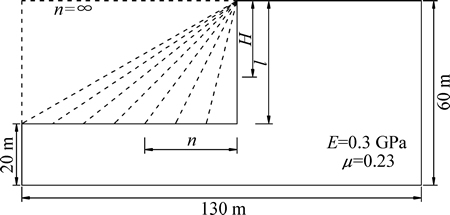
图1 数值试验模型示意图
Fig. 1 Schematic of numerical test model
由图2可见:主应力随H增大而线性增大,对坡比下数据进行线性拟合后得到如图3所示线性参数(斜率和截距),分析其线性参数可知,在不同坡比下斜率几乎不变,与自重应力(γH)变化规律一致(均质边坡中重度γ不变)。当n=∞时,同一点处主应力都比其他坡比的大(图2中最高线),说明利用自重应力在建立解析计算公式中偏保守。综合上述分析可知:边坡内部应力简化为垂直自重应力和相应的水平侧压力2部分,不但变化规律与实际应力状态一致,而且对于工程应用中偏安全,因此,这种简化是合理的。
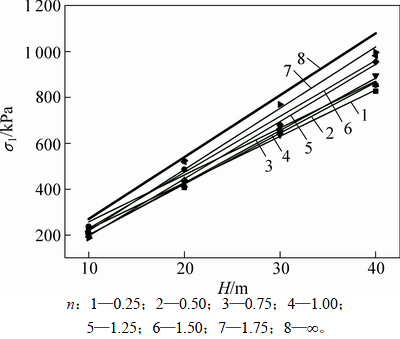
图2 主应力随H变化规律
Fig. 2 Rule of principal stress change with H
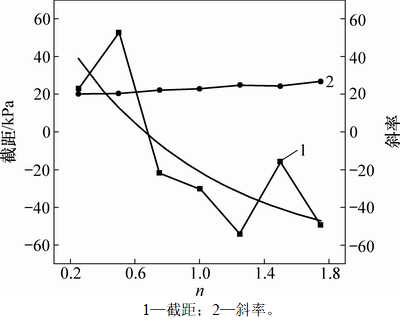
图3 线性参数
Fig. 3 Linear parameter
1.2 计算公式推导
图4所示为反倾边坡中岩层受力图。取边坡任意岩梁(岩层)作为受力分析对象,以岩梁顶点A距坡顶距离H(坡顶距)反映岩梁在边坡中空间位置情况,岩梁任意点B(x处)受上部岩梁重力σv及侧向压力σH为:
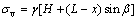 (1)
(1)
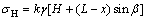 (2)
(2)
式中:γ为岩体重度,本文相关计算中取27 kN/m3;k为侧压力系数,本文相关计算中取0.3。
将其分解为法向作用力F和切向作用力T为:
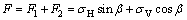 (3)
(3)
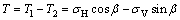 (4)
(4)
与此同时法向作用力F产生层间摩擦力f为
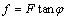 (5)
(5)
式中:φ为层间内摩擦角,(°)。
图5所示为锚固受力分析图。在xoy平面分析情况下取单位岩梁宽度(z方向取单位1),岩梁厚度为h,则单位岩梁长度自重G为
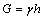 (6)
(6)
式中:h为岩梁厚度,m。
图5所示为锚固受力分析图。由图5可知:岩层未折断前,在局部坐标系任意x处重力y分量、法向力F通过对o点的弯矩作用使岩层上下边界分别产生拉压应力;重力x分量、层间摩擦力f在岩层上边界直接产生压应力;切向力T在岩层上边界直接产生拉应力,其中层间摩擦力和切向力都是作用在单位长度而产生应力,为让表达式物理意义更加明确,从而总拉应力公式表达为
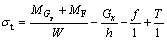 (7)
(7)
式中:Gx和Gy分别为重力x分量Gx=Gsinβ和重力y分量Gy=Gcosβ,kN/m;MGy和MF分别为y方向重力分量和法向力形成的弯矩,kN·m;W为岩层抗弯截面模量W=h2/6,m2。
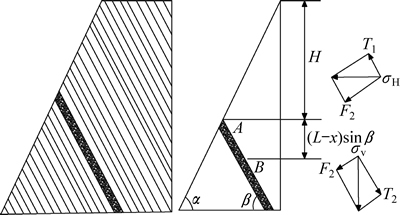
图4 反倾边坡中岩层受力图
Fig. 4 Mechanics analysis diagram
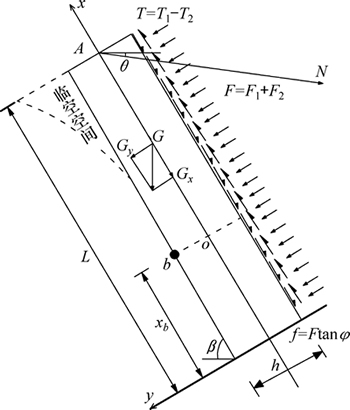
图5 锚固受力分析图
Fig. 5 Anchoring force analysis diagram
为求出折断深度(L-xb),以确定折断后倾倒转动中心点o,按最大拉应力破坏准则(一般情况岩体抗压强度大于抗拉强度):
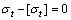 (8)
(8)
式(8)中[σt]以广义Hoek-Brown准则[18]确定。该准则是基于大量现场岩体原位试验与室内岩石三轴试验资料成果统计分析结果,并综合了岩体结构特征、节理发育特征、地应力、岩块强度等多方面的影响而得出的岩体破坏准则。其表达式如下:
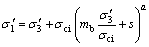 (9)
(9)
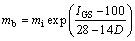 (10)
(10)
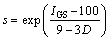 (11)
(11)
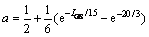 (12)
(12)
式中: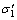 为岩体破坏时最大有效主应力,MPa;
为岩体破坏时最大有效主应力,MPa; 为岩体破坏时最小有效主应力,MPa;
为岩体破坏时最小有效主应力,MPa; 为岩块单轴抗压强度,MPa;mi为完整岩块材料常数,可通过对岩块的三轴试验数据进行拟合得到或按岩石类型确定;D 为扰动系数;IGS为Hoek等提出的地质强度指标;a为Hoek-Brown强度参数。
为岩块单轴抗压强度,MPa;mi为完整岩块材料常数,可通过对岩块的三轴试验数据进行拟合得到或按岩石类型确定;D 为扰动系数;IGS为Hoek等提出的地质强度指标;a为Hoek-Brown强度参数。
当 =0时,通过式(9)可得:
=0时,通过式(9)可得:
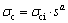 (13)
(13)
当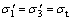 时,由式(9)可得:
时,由式(9)可得:
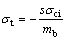 (14)
(14)
采用广义Hoek-Brown准则进行岩体参数估算时,只需获取 ,mi,D和IGS等参数即可。前2个参数可利用室内岩石三轴试验获取;扰动系数D可采用HOEK等[19]建议的方法确定;IGS可根据GSI岩体分级体系确定。
,mi,D和IGS等参数即可。前2个参数可利用室内岩石三轴试验获取;扰动系数D可采用HOEK等[19]建议的方法确定;IGS可根据GSI岩体分级体系确定。
边坡岩层经历了弯曲-折断过程后,从而绕b点倾倒,在局部坐标系下重力x分量、层间摩擦力f将产生抵抗力矩,而重力y分量、法向力F、切向力T将倾覆力矩,若未进行锚固(无锚固力作用),则定义锚固前稳定系数为抵抗力矩与倾覆力矩之比:
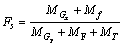 (15)
(15)
代入各分量得:
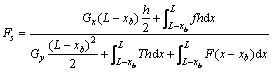 (16)
(16)
当进行边坡锚固设计时,设锚固力N作用于岩层顶端,俯角为θ。为提供最大抵抗力矩,锚索应尽可能与岩层垂直,这与文献[9]所提出的串层锚杆原理一致,若这样设置锚索,则无法保证锚索锚固段能够锚固于稳定地层或岩体质量较好的地层之中,况且考虑到实际施工注浆工艺等要求,规范规定俯角不能小于10°,故取锚索俯角最小值θ=10°。在保证所需安全裕度(安全系数)下满足力矩平衡条件,则锚固后安全系数定义为抵抗力矩与倾覆力矩之比:
 (17)
(17)
通过等式变换进而得出锚固力计算公式为
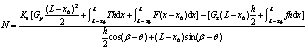 (18)
(18)
2 工程实例应用
2.1 地质条件
以雅鲁藏布江某水电站导流明渠边坡为例(图6),边坡所在山体雄厚,河谷深切但开阔,呈U型宽谷(图7),现代河床偏左岸,江水流向N60°E,枯水期水位约3 203 m。两岸阶地发育,边坡前缘江边下部为基岩陡坎,基岩面拔河高8~20 m。开挖前自然斜坡表面平顺,坡度55°~60°,开挖后岩面起伏较大,或呈岩埂,或局部呈深槽。出露地层主要为郎杰学群姐德秀组第一段第四层(T3j1-4)硅质板岩、绢云母石英片岩、变质砂岩夹炭质板岩,第四系冲洪积、崩坡积物零星分布。边坡中上部以硅质板岩、绢云母石英片岩为主,呈薄层状不等厚互层陡倾坡内,岩性偏软;下部以中-厚层状变质砂岩夹炭质板岩为主,属中硬岩,总体呈上软下硬坡体结构。调查、统计表明研究区节理裂隙主要发育有4组:1)层面裂隙,产状近EW/S∠50°~70°,较发育-发育,与岸坡小角度相交,延伸>10 m,平直粗糙,局部充填岩屑,中等锈染-新鲜,间距5~60 cm不等;2) 产状近SN/W∠80°~85°,发育,与岸坡大角度相交,延伸为3~10 m,平直粗糙,微张,局部充填岩屑,中等锈染,呈密集发育,间距5~10 cm;3) 产状N50°~60°W /NE∠40°~45°,较发育,出露于岸边基岩露头,与岸坡小角度相交,延伸短小,断续延伸,平直粗糙,微张,新鲜-中锈,间距>100 cm;4) 产状近EW/N∠20°~30°,较发育,在平硐中出露,与岸坡小角度相交,延伸短小,断续延伸,平直粗糙,微张,充填脉石英,新鲜—中锈,间距>100 cm。

图6 开挖实景图
Fig. 6 Excavation diagram
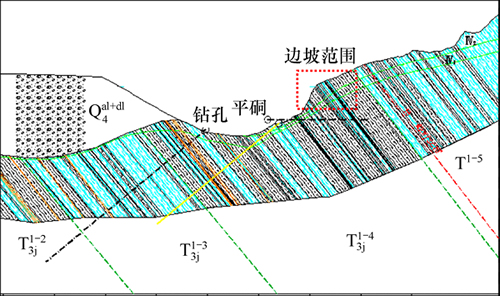
图7 区域工程地质剖面图
Fig. 7 Regional engineering geological profile diagram
2.2 地质模型
通过地表调查、探槽揭露,发现边坡开挖后以中上部低强度薄层状岩体弯曲倾倒为主,越靠近1号冲沟变形越明显,而所占比例相对较少的下部硬质中-厚层状岩体变形甚微,边坡处置应重点放在中上部变形岩体,提高其岩体强度,抵抗岩体弯曲倾倒。边坡原有地形为凸出山梁(图7),建立计算模型时忽略内侧山体以及下部未变形岩体。边坡开口线至岩性分界线(未变形岩体上边界)高差约40 m,则取计算模型坡高40 m(图8)。按既有设计资料以及相关规范,开挖坡比取1:0.5,安全等级定为一级,安全系数取Ks=1.3。
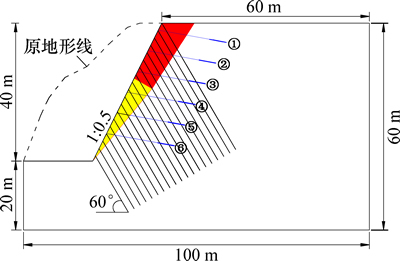
图8 边坡计算剖面
Fig. 8 Calculation section of slope
产生弯曲变形从而折断破坏的这类边坡多是由岩性较软、中—薄层状岩体组成的[20],本实例就属此类(层厚5~10 cm)。在这种情况下,薄层状岩层几何大小对整个边坡而言相当于薄板,根据材料力学或弹性力学可知,薄板弯曲计算与悬臂梁弯曲计算假设条件并不一样,若要按前文中悬臂梁弯曲理论推导的公式进行计算,则需要寻找一种“增厚的岩层”来满足要求,故以实际层厚计算意义不大。与此同时,后文数值模拟评价中建模将出现过多单元,导致计算机无法完成模拟,故此,建立“等效层厚”概念以满足计算需要。如前所述,等效层厚概念需满足3个条件:1) 等效层厚岩体是包含岩块与结构面(包括节理面与真实层面)组合后的均质体,以进行“增厚”;2) 数值模型能够完成计算;3) 边坡变形破坏仍以弯曲倾倒为主,即与实际变形破坏现象一致。对于条件1):可在场区地质调查基础上,结合室内试验、原位试验以及钻孔摄像等资料,采用前文中介绍的Hoek-Brown经验准则确定等效层厚岩体参数(表1);对于条件2)和3):按图8所示边坡尺寸、表1中岩体参数、表2中岩层层面参数建立二维离散元数值模型,左右边界固定水平位移,下边界固定垂直位移,上边界为自由边界,只考虑自重应力场。在其余参数不变情况下分别模拟等效层厚取1,2,3,…,10 m时坡顶水平位移和变形面积百分比变化规律(图9),其中变形面积主要考虑节点水平位移大于10 cm的单元,通过fish语言编制变形面积计算程序进行不同层厚变形面积百分比计算,计算公式为:S=S′/S0(式中:S′为变形单元面积之和,S0为计算模型区域内所有单元面积之和)。
从图9模拟结果可知:坡顶水平位移和变形面积百分比都随层厚变大而先增后减,前者峰值在h=6.5 m左右,后者在h=2.2 m左右。从坡顶水平位移来看,按极限方法考虑,若层厚无限小退化到横贯各向同性体,或层厚无限大退化到完整均质体,则都不会发生明显弯曲变形(坡顶水平位移不大),那么中间必存在一个过渡区(阈值h=6.5 m),同时由大量工程案例来 看[20],发生弯曲倾倒往往都发生在中—薄层状岩体,故本实例等效层厚上限值取6.5 m。同理按极限方法考虑,变形面积百分比同样存在1个过渡区(阈值h=2.2 m),在本工程案例边坡实际平硐调查中,除硐口以内6 m范围有明显卸荷裂隙、弯曲折断外,平硐内未见明显大尺寸折断带,同时通过地表探槽即发现折断带出露(图10),推测该边坡折断深度不超过6 m,即边坡发生大变形的面积不大,故根据实际调查结果,进一步缩小本实例等效层厚上限值为2.2 m。等效层厚在满足数值模拟计算的同时不超过2.2 m,都是可取的,为方便计算,本文锚固计算中选定等效层厚为h=2 m。
表1 基于Hoek-Brown准则的岩体参数估算结果
Table 1 Rock mass parameters estimation result with Hoek Brown criterion

表2 岩层层面力学参数
Table 2 Strata interface mechanical parameters

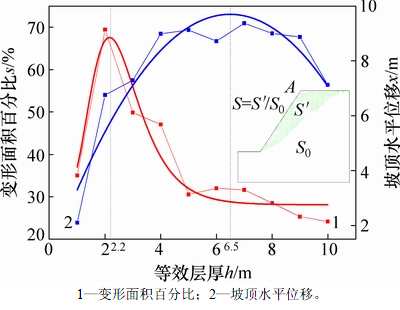
图9 等效层厚分析图
Fig. 9 Equivalent thickness analysis diagram

图10 探槽揭露折断带
Fig. 10 Exploratory trench reveal broken belt
2.3 锚固力计算过程
上述锚固力计算方法可通过MATLAB编程实现,计算过程如下:
1) 令折断深度L-xb=l,将式(1)~(6)代入式(7),再将式(7)代入式(8),最终整理得出三次多项式方程:Al3+Bl2+Cl+D=0。式中:
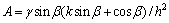
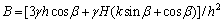
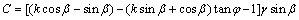
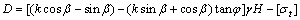
2) 以牛顿迭代法求解上述三次多项式方程,控制精度为1×10-5。为减少计算次数,间距2 m坡顶距依次计算折断深度(实际应用可根据需要调整计算间距)。
3) 求出折断深度后,将其代入对应的稳定系数公式(式(16))和锚固力计算公式(式(18)),当锚固力为负值即可停止计算,详细见计算结果表(表3)和对应图示(图11)。
从计算结果来看,随坡顶距增大,折断深度减小, 最大折断深度不超过6 m,与实际调查情况较为符合; 稳定系数随坡顶距增大而增大,说明越往下随临空条件越差,弯曲倾倒越不易,稳定性越好;锚固力随坡顶距增大而减小,最大锚固力339.69 kN/m。在H=16~40 m范围(图8中黄色部分),稳定系数大于设计安全系数,锚固力计算值为负,若按本文介绍的计算模型来说安全裕度足够,不需要支护,但如果这部分岩体完全稳固,如何提供上部倾倒岩层下侧面临空条件的假定,根据汪小刚等[21]利用离心模型研究岩质边坡倾倒破坏研究成果,认为这部分岩体以滑动破坏为主。本文计算模型出发点是以上部弯曲倾倒岩层锚固为目的,而在实际工程设计中,还需要结合滑动破坏计算模型[8],考虑边坡下部岩体稳定性计算锚固力及确定锚固位置,其中滑面是从坡脚剪出的直线型滑面(图8)。
表3 计算结果
Table 3 Calculation results
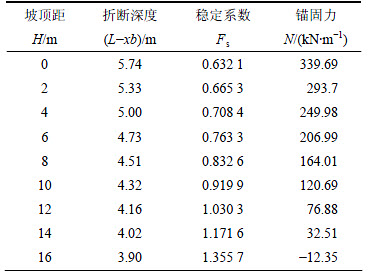
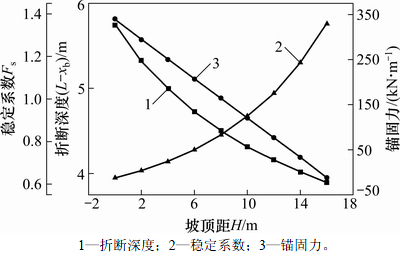
图11 计算结果图
Fig. 11 Figure of calculation results
2.4 参数敏感性分析
已有的研究结果表明[2-4]:岩层厚度、岩体抗拉强度、层间内摩擦角对整个坡体的稳定性影响较大,根据实际工程情况,分别选取岩体抗拉强度和层间内摩擦角取值范围为0.75~1.50 MPa和9°~18°,而层厚取值范围根据前文分析结果取0.5~2.0 m,对三者进行敏感性分析时,其他参数保持不变。图12所示为三者对边坡锚固模式的影响,倾倒锚固区随层厚和抗拉强度减小而减小,而随层间内摩擦角减小无明显变化,说明层厚和抗拉强度对锚固模式的影响较大。图13和图14所示分别为三者对最大折断深度和最大锚固力的影响,最大折断深度与最大锚固力都随层厚和抗拉强度增大而增大,与前人基于悬臂梁模型分析倾倒变形体折断深度与层厚呈正相关关系[22]的结论一致。层厚和抗拉强度都对折断深度和锚固力有较大影响,而层间内摩擦角影响较小,而进一步比较可知,层厚较之抗拉强度影响程度更大(拟合直线更陡)。综上所述,此类边坡锚固设计对这3个参数敏感性由大到小依次为:层厚、抗拉强度、层间内摩擦角。
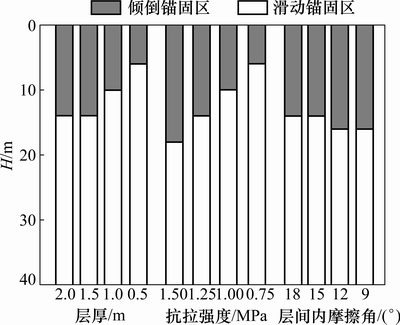
图12 参数对锚固区划分影响
Fig. 12 Parameters impact on anchoring zone division

图13 最大折断深度对参数敏感性
Fig. 13 Max broken depth sensitivity to parameters
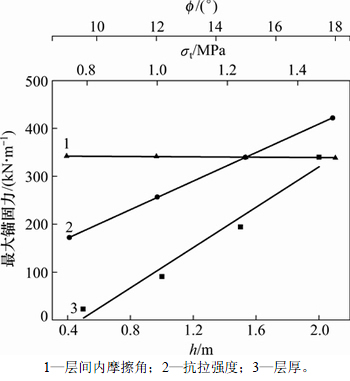
图14 最大锚固力对参数敏感性
Fig. 14 Max anchoring force sensitivity to parameters
3 边坡锚固数值模拟
通过建立边坡锚固数值模型,分别模拟分析边坡上部锚固和下部锚固2种工况下边坡应力应变过程,得出锚索轴力和边坡水平位移变化规律,并与前文解析计算结果进行比较。
按图8所示边坡尺寸、表1中岩体参数、表2中岩层层面参数建立二维离散元数值模型,左右边界固定水平位移,下边界固定垂直位移,上边界为自由边界,只考虑自重应力场。工况一:边坡上部以1~3号锚索锚固;工况二:下部以4~6号锚索锚固(图8)。在这2种工况下,1~6号锚索与锚固墩力学参数相同,锚索间距为6 m,根据相关规范,单锚自由段和锚固段都分别取15 m和5 m(忽略张拉预留长度),锚固墩取0.8 m。UDEC中以锚杆单元(cable)模拟锚索,共需要6个参数(表4),其中锚杆体4个参数以及砂浆体2个参数,自由段通过设置砂浆体黏结强度为0实现,cable单元可直接设置预应力;锚固墩以梁单元(structure)模拟,共需要7个参数(表5),其中梁体本身2个,梁与岩体接触5个。锚固墩与锚索之间需固定铰接,UDEC中cable单元与structure单元共用节点时自动实现固定铰接状态。
数值模拟中为反映锚固力变化规律,定义锚索轴力增量比为:η=(Fj-Fy)/Fy(式中:Fj为模拟锚索轴,Fy为锚杆单元设置的预应力参数)。图15所示为锚索轴力增量比。由图15可知:上部锚固系统中锚索轴力增量比随坡顶距增大而减小,与前文解析计算结果变化规律一致。另外,上部锚索轴力增量总体大于下部锚索轴力增量,上部锚索承受更大的拉力,即上部更需要加固。
图16所示为水平位移云图与轴力图,图中ux为水平位移。由图16可知:在边坡上部锚固后最大水平位移区域转移到坡体中部,而锚固下部后边坡最大水平位移仍在坡顶区域附近,且最大水平位移量级(8 cm)区域面积前者明显比后者的小,说明锚固边坡上部(即倾倒锚固区)对于控制边坡变形来说效果更加明显。
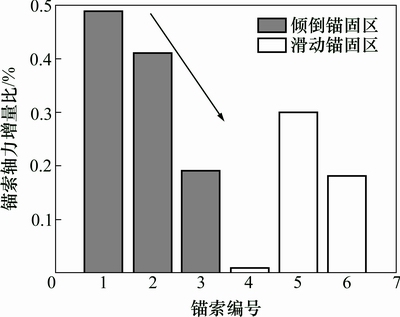
图15 锚索轴力增量比
Fig. 15 Anchor axial force increment ratio
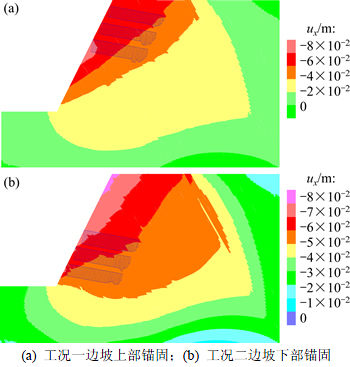
图16 水平位移云图与轴力图
Fig. 16 Horizontal displacement nephogram and axial force figure
表4 锚杆单元参数
Table 4 Anchor parameter

表5 喷射混凝土单元参数
Table 5 Sprayed concrete parameter

4 结论
1) 基于悬臂梁理论建立的锚固力计算模型,要获得解析解而需将斜坡中一点应力状态简化为自重应力和侧压力,通过数值试验解释了这种简化的合理性。
2) 以满足参数可取、数值可算、变形破坏现象与实际情况一致3个条件建立等效层厚概念,确定本实例等效层厚取值不应超过2.2 m。
3) 锚固区可划分为倾倒锚固区和滑动锚固区,其中倾倒锚固区折断深度和锚固力都随坡顶距增大而减小,最大折断深度不超过6 m,符合实际情况,不支护条件下稳定系数随坡顶距增大而增大,在H=12 m左右岩体达到极限平衡(Fs=1.0)。
4) 通过对岩层厚度、岩体抗拉强度、层间内摩擦角3个参数进行敏感性分析,此类边坡锚固设计对这3个参数敏感性由大到小依次为:层厚、抗拉强度、层间内摩擦角。
5) 上部锚固系统中锚索轴力增量比(η)随坡顶距增大而减小,即与倾倒锚固区锚固力解析计算值变化规律一致。另外,上部锚索轴力增量总体大于下部锚索轴力增量,以及上部锚固后明显控制了边坡水平位移,即加固倾倒锚固区比加固滑动锚固区对于控制边坡水平位移效果更加明显。
6) 文中所选计算模型虽然计算结果相对保守,但并不能说明就是合理的,因为工程上除了安全性考虑以外,还需考虑经济性,这也是本文研究不足之处,在实际工程应用时应该进行权衡和比较。
参考文献:
[1] GOODMAN R E, BRAY J W. Toppling of rock slopes[C]//Proceedings of Specialty Conference on Rock Engineering for Foundations and Slopes. Boulder, CO: ASCE, 1977: 201-234.
[2] ZANBAK C. Design charts for rock slopes susceptible to toppling[J]. Journal of Geotechnical Engineering, 1983, 109(8): 1039-1062.
[3] ISHIDA T, CHIGIRA M, HIBINO S. Application of the distinct element method for analysis of toppling observed on a fissured slope[J]. Rock Mechanics and Rock Engineering, 1987, 20(4): 277-283.
[4] AYDAN O, SHIMIZU Y, ICHIKAWA Y. The effective failure modes and stability of slopes in rock mass with two discontinuity sets[J]. Rock Mechanics and Rock Engineering, 1989, 22(3): 163-188.
[5] 陈祖煜, 张建红, 汪小刚. 岩石边坡倾倒稳定分析的简化方法[J]. 岩土工程学报, 1996, 18(6): 92-95.
CHEN Zuyu, ZHANG Jianhong, WANG Xiao-gang. A simplified method for toppling stability analysis of rock slopes[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(6): 92-95.
[6] 孙东亚, 彭一江, 王兴珍. DDA数值方法在岩质边坡倾倒破坏分析中的应用[J]. 岩石力学与工程学报, 2002, 21(1): 39-42.
SUN Dongya, PENG Yijiang, WANG Xingzhen. Application of DDA method to stability analysis of toppling rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(1): 39-42.
[7] 汪小刚, 贾志欣, 陈祖煜, 等. 岩质边坡倾倒破坏的稳定分析方法[J]. 水利学报, 1996(3): 7-21.
WANG Xiaogang, JIA Zhixin, CHEN Zuyu, et al. The research of stability analysis of toppling failure of jointed rock slopes[J]. Journal of Hydraulic Engineering, 1996(3): 7-21.
[8] 程良奎, 李象范. 岩土锚固-土钉-喷射混凝土原理设计与应用[M]. 北京: 中国建筑工业出版社, 2008: 249-250.
CHEN Liangkui, LI Xiangfan. Geotechnical anchoring-nailing- shotcrete principle design and application[M]. Beijing: China Building Industry Press, 2008: 249-250.
[9] 张布荣. 倾倒型岩石边坡工程加固的研究[J]. 土木工程学报, 1995, 28(5): 70-75.
ZHANG Burong. Study on strengthening technique for toppling rock slope[J]. China Civil Engineering Journal, 1995, 28(5): 70-75.
[10] SAGASETA C, SANCHEZ J M, CANIZAL J. A general analytical solution for the required anchor force in rock slopes with toppling failure[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 421-435.
[11] LIU C H, JAKSA M B, MEYERS A G. A transfer coefficient method for rock slope toppling[J]. Canadian Geotechnical Journal, 2009, 46(1): 1-9.
[12] LIU C H, JAKSA M B, MEYERS A G. Toppling mechanisms of rock slopes considering stabilization from the underlying rock mass[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 348-354.
[13] 杨保军, 何杰, 吉刚, 等. 岩质边坡滑动-倾倒组合破坏模式稳定性分析[J]. 岩土力学, 2014, 35(8): 2335-2352.
YANG Baojun, HE Jie, JI Gang, et al. Stability analysis of sliding-toppling complex failure of rock slope[J]. Rock and Soil Mechanics, 2014, 35(8): 2335-2352.
[14] 黄润秋. 高边坡稳定性的系统工程地质研究[M]. 成都: 成都科技大学出版社, 1991: 124-126.
HUANG Runqiu. The stability of high slope engineering geological system research[M]. Chengdu: Chengdu University of Science and Technology Press, 1991: 124-126.
[15] 殷坤龙, 周春梅, 柴波. 三峡库区巫峡段反倾岩石边坡的破坏机制及判据[J]. 岩石力学与工程学报, 2014, 33(8): 1635-1643.
YIN Kunlong, ZHOU Chunmei, CHAI Bo. Failure mechanism and criterion of counter-tilt rock slopes at Wuxia gorge section in three gorges reservoir area[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1635-1643.
[16] 陈红旗, 黄润秋. 反倾层状边坡弯曲折断的应力及挠度判据[J]. 工程地质学报, 2004, 12(3): 243-273.
CHEN Hongqi, HUANG Runqiu. Stress and flexibility criteria of bending and breaking in a countertendency layered slope[J]. Journal of Engineering Geology, 2004, 12(3): 243-273.
[17] 齐典涛. 昌马水库倾倒变形边坡特征形成机制及发育深度[J]. 西部探矿工程, 2001(6): 47-49.
QI Diantao. The formation mechanism and development depth of the toppling slope in Changma reservoir[J]. West-China Exploration Engineering, 2001(6): 47-49.
[18] HOEK E, CARRANZA-TORRES C, CORKUM B. Hoek-Brown failure criterion: 2002 edition[C]//Proceedings of NARMS-Tac Conference. Toronto, 2002: 267-273.
[19] HOEK E, BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186.
[20] 黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-455.
HUANG Runqiu. Large-scale landslides and their sliding mechanisms in china since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-455.
[21] 汪小刚, 张建红, 赵毓芝, 等. 用离心模型研究岩石边坡的倾倒破坏[J]. 岩土工程学报, 1996, 18(5): 14-21.
WANG Xiaogang, ZHANG Jianhong, ZHAO Liuzhi, et al. Investigations on mechanism of slope toppling failureby centrifuge model testing[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(5): 14-21.
[22] 丁小军, 刘卫民, 王佐, 等. 软质岩边坡倾倒变形机理及处治工程实例[M]. 北京: 人民交通出版社, 2011: 26-29.
DING Xiaojun, LIU Weimin, WANG Zuo, et al. Dumping soft rock slope deformation mechanism and example of treatment engineering[M]. Beijing: China Communications Press, 2011: 26-29.
(编辑 杨幼平)
收稿日期:2016-10-25;修回日期:2017-02-14
基金项目(Foundation item):国家重点基础研究发展计划(973计划)项目(2011CB710605);中国电建集团成都勘测设计院有限公司科技项目(P225-2014)(Project (2011CB710605) supported by the National Basic Research Development Program (973 Program) of China; Project (P225-2014) supported by the Science and Technology Project of Power China Chengdu Engineering Corporation Limited)
通信作者:晏鄂川,博士,教授,从事岩土体稳定性评价与利用研究;E-mail:yecyec6970@163.com