基于KPLS特征提取的WNN模拟电路软故障诊断
丛伟,景博,于宏坤
(空军工程大学 航空航天工程学院,陕西 西安,710038)
摘要:为提高模拟电路的软故障诊断能力,提出一种基于KPLS特征提取和WNN的集成诊断方法。首先利用KPLS良好的特征提取能力,构建故障样本集的主元特征集;然后,利用WNN解决复杂非线性问题的优势,建立主元特征集的故障识别模型;最后,由所建模型对各种故障模式进行诊断判定。Sallen-Key带通滤波器的仿真测试表明:该集成方法仅通过不到300次迭代计算即完成模型训练,诊断的总正确率达到96.7%,且9种模式中的6种达到100%正确率,从而验证了其可行性和有效性。
关键词:小波神经网络;核偏最小二乘;特征提取;模拟电路;故障诊断
中图分类号:TP181;TM930 文献标志码:A 文章编号:1672-7207(2014)06-1841-06
WNN soft fault diagnosis of analog circuit based on KPLS feature extraction
CONG Wei, JING Bo, YU Hongkun
(College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’an 710038, China)
Abstract: In order to improve the ability of soft fault diagnosis of analog circuits, an integrated diagnosis method based on KPLS feature extraction and WNN was proposed. First, the good feature extraction ability of KPLS was used to construct the principal element feature set of fault sample set; then, the advantages of WNN on solving the complicated nonlinearity problems was applied to establish the fault identification model based on principal element feature set; finally, each failure mode was diagnosed and determined by the built model. The simulation experiment of Sallen-Key bandpass filter shows that the integrated method just completes the training of the model by less than 300 iterations computation with the total correct rate 96.7%, and the correct rate of 6 modes in 9 modes reaches 100%, which verifies its feasibility and effectiveness.
Key words: wavelet neural network; kernel partial least square; feature extraction; analog circuit; fault diagnosis
随着计算机和电子技术的飞速发展,电子设备的种类越来越繁杂,复杂性越来越高,正确诊断模拟电路故障也变得越来越困难。模拟电路的硬故障,如开路或短路,会造成电路和系统的崩溃,通常容易诊断,而容差问题造成的软故障,故障模式具有模糊性和不确定性,不易识别,这类故障往往会引起电路和系统性能的逐渐恶化,必须对其准确诊断和定位,也是目前的研究热点之一。模拟电路的软故障诊断本质上是一个模式识别和分类问题,即将给定的故障数据划分为正常数据和故障数据。随着模拟电路故障诊断技术研究的深入,出现了故障字典法、参数辨识法、故障验证法等诸多软故障诊断方法[1-3],实践和数值分析表明:元器件发生软故障时,其参数可能在零到无穷大之间连续变化,而不同的偏移会引起不同的电路响应,电路的状态数可能是无穷的。将这些诊断方法用于软故障诊断,其计算量是现有计算机无法胜任的[4]。神经网络技术改变了模拟电路软故障诊断的既有模式,但其准确率不高、收敛较慢、过拟合和易陷入局部极小等问题,限制了它的推广[5-8]。小波神经网络 (wavelet neural network, WNN) 是在小波理论基础上发展起来的一种新型神经网络,它较好地融合了小波变换的时频局域特性和神经网络的自学习功能,性能得到较大改善,理论也更趋于严密,是公认的神经网络替代方法[9-10]。然而,作为一种新兴的模式识别方法,WNN存在着一些亟待解决的问题,如,WNN不具备特征提取功能,而模拟电路的故障样本数据的属性较多,并且不同来源的噪声污染,属性间不同程度的多重相关性,都可能影响模型的复杂性和性能,有必要在WNN建模前预先提取属性的特征。基于以上分析,本文提出一种基于核偏最小二乘 (kernel partial least square, KPLS) 和WNN的集成诊断方法,即先采用KPLS对故障样本数据进行特征提取,再利用WNN对所提取特征建立模拟电路的软故障诊断模型,以满足诊断的准确性和实用性的要求。
1 核PLS分析
1.1 核方法基本原理
核函数定义:若x和y都是空间X中的向量,f(·)为能将输入空间X变量映射到特征空间H的非线性函数,如果函数 满足Mercer条件,则称K(x,y)为核函数 (符号
满足Mercer条件,则称K(x,y)为核函数 (符号 代表内积)[11-12]。通常也把采用核函数技术的一类方法称为核函数方法,其基本原理是通过函数f(·)把输入空间映射到高维特征空间 (可以是无穷维),然后在该特征空间中进行分类或回归等处理,其原理如图1所示。
代表内积)[11-12]。通常也把采用核函数技术的一类方法称为核函数方法,其基本原理是通过函数f(·)把输入空间映射到高维特征空间 (可以是无穷维),然后在该特征空间中进行分类或回归等处理,其原理如图1所示。
其关键在于通过引入核函数,把非线性变换后的高维特征空间的内积运算转换为原输入空间中的核函数的计算,即通过 来实现的。这样,在特征空间的线性计算即对应原输入空间的非线性算法[13-14]。
来实现的。这样,在特征空间的线性计算即对应原输入空间的非线性算法[13-14]。
核函数本质上是个内积 (或点积),也是核技巧的基础。概括起来,核函数方法的主要特点为:核函数计算没有涉及特征空间的维数;无需明确映射函数f(·)的具体形式和参数;核函数的不同形式对应着不同的非线性映射函数;核函数方法与不同算法结合,可以形成解决不同问题的基于核函数技术的算法。
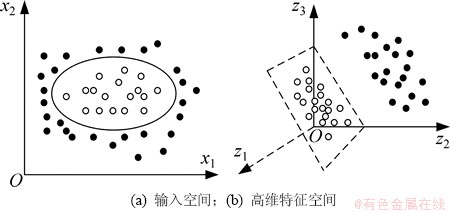
图1 核函数方法原理图
Fig. 1 Schematics of kernel function method
1.2 核PLS特征提取
偏最小二乘回归 (partial least squares, PLS) 是一种将主元分析、相关性分析和自回归分析相结合的统计学建模方法。鉴于PLS是一种线性分析方法及其处理非线性问题的不足,Rosipal等[15]将核函数技术引入PLS方法,进而提出KPLS方法。其基本思想是将输入空间X通过非线性函数f(·)映射到高维特征空间H,然后在该特征空间运用PLS方法。这样特征空间的线性PLS即对应原输入空间X的非线性关系。该方法可以作为非线性特征提取器和其他方法结合使用。但使用前需对样本数据预先进行核函数变换和核矩阵中心化处理。
设训练样本集为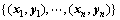 ,测试样本集为
,测试样本集为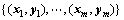 ,
, ,
, ,d为自变量维数,c为自变量维数。先对样本数据进行标准化处理,再对训练和测试样本的输入矩阵
,d为自变量维数,c为自变量维数。先对样本数据进行标准化处理,再对训练和测试样本的输入矩阵 和
和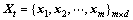 进行核函数变换,可构造核函数内积矩阵K和Kt:
进行核函数变换,可构造核函数内积矩阵K和Kt:
 (1)
(1)
 (2)
(2)
式中,i=1,2,…,n;j=1,2,…,n;l=1,2,…,m;xi和xj为X的向量;xl为Xt的向量。
由于KPLS是在映射数据为零均值假设下推导出来的,需要对K和Kt中心化处理,中心化的核矩阵 和
和 可由下式求得:
可由下式求得:
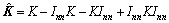 (3)
(3)
 (4)
(4)
式中:Inn为所有元素为1/n的n×n阶方阵,Imn为所有元素为1/n的m×n阶矩阵。
根据式 (1) 和式 (2) 得到的核矩阵,可给出一种KPLS算法的伪代码。
初始化:K1= ,YY=Y,s=0
,YY=Y,s=0
For i=1到p
YK=YY·YYT·Kt
ui=YY(:,1)/||YY(;,1)||
If YY维数大于1
η=ui+1
While ||ui-η||>0.001 & s<50
s=ε+1
η=ui
ξ=YK·η
ui=ξ/||ξ||
end
end
ti=Kiui
ci=YYT·ti/||ti||2
wi=Kt·ti/||ti||2
Ki+1=Ki-ti·wiT-wi·tiT+titiT·(tiTwi)/||ti||2
YY=YY-t2·ciT
end
迭代过程结束后,可得到p个主元,T=[t1,…,tp]和U=[u1,…,up]。通过T和U也可计算出训练样本的 的特征向量。
的特征向量。
 (5)
(5)
将式(4)代入式(6),可得测试样本的 的投影矩阵:
的投影矩阵:

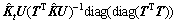 (6)
(6)
式中:diag(·)为矩阵对角算子。
一般来说,KPLS提取的主元包含了较多的非线性特征,因此其主元数通常要多于PLS提取的主元数,最多可提取rank(K)个主元。对于采用KPLS提取的主元,可作为其他线性或非线性算法的输入,从而构成集成KPLS算法。
2 小波神经网络
小波神经网络是一种新型前馈神经网络。它以小波理论为基础,较好地融合了小波变换的时频局域特性和神经网络的自学习功能,性能得到较大改善,理论也更趋于严密。
对于结构如图2所示的WNN,其网络输入为xi(i=1,…,I),网络输出为yk(k=1,…,K),而wji(j=1,…,J;i=1,…,I)为输入层至隐含层的连接权值,wkj(k=1,…,K;j=1,…,J)为隐含层至输出层的连接权值,且I,J,K分别为输入层、隐含层和输出层的节点个数。则该网络的输出为
 且
且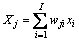 (7)
(7)
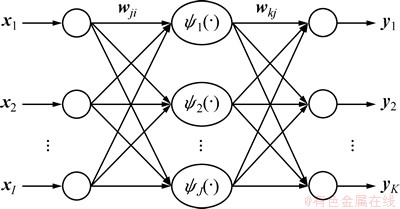
图2 WNN的基本结构
Fig. 2 Basic structure of WNN
式中:k=1,…,K;j=1,…,J;aj和bj分别为伸缩参数和平移参数。
对于图2所示网络,选用的小波基函数不同,其构成的学习算法也不相同。本文以Mexican hat小波作为基函数,即 ,则参考常规BP算法引入动量项,网络各参数可按下式进行调整:
,则参考常规BP算法引入动量项,网络各参数可按下式进行调整:
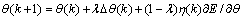 (8)
(8)
式中:θ代表wji,wkj,aj和bj参数;Δθ(k)为上次调整后的参数差值; 为各参数的瞬时梯度向量,即
为各参数的瞬时梯度向量,即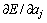 ,
, ,
, 和
和 ;λ为动量系数,它可以降低网络对于误差曲面细节的敏感性,有效地抑制陷入局部极小;η(k)为学习速率,它的选取非常重要,取太小则收敛速度慢,且易陷入局部极小;取太大则收敛速度快,但可能会产生振荡[16]。因此,可采用自适应学习率动态调整η(k),具体调整公式如下:
;λ为动量系数,它可以降低网络对于误差曲面细节的敏感性,有效地抑制陷入局部极小;η(k)为学习速率,它的选取非常重要,取太小则收敛速度慢,且易陷入局部极小;取太大则收敛速度快,但可能会产生振荡[16]。因此,可采用自适应学习率动态调整η(k),具体调整公式如下:
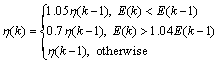 (9)
(9)
式中:1.05,0.7和1.04都为经验值。
3 KPLS-WNN集成算法
KPLS-WNN的基本原理是用KPLS进行特征提取,再以提取的主元作为WNN模型的输入,建立如图3所示的KPLS与WNN集成模型。具体实现步骤如下。
(1) 主元提取。
1) 选择合适的核函数,计算核矩阵K和Kt,然后由式 (3) 和式(4)得到中心化的核矩阵 和
和 ;
;
2) 通过KPLS算法计算主元矩阵T,并由式 (5) 计算出 的特征矩阵Fea;
的特征矩阵Fea;
3) 利用式(6)计算测试样本的 的投影,建立新的测试样本集Ttest。
的投影,建立新的测试样本集Ttest。
(2) 训练模型。以T为训练输入,Y为输出,选择适当参数建立WNN模型。
(3) 测试验证。以Ttest为测试输入,检验建立的WNN模型,输出测试结果和分类精度。
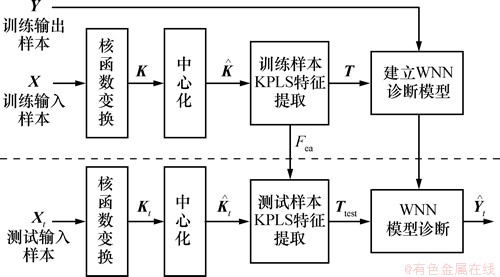
图3 KPLS-WNN故障诊断原理
Fig. 3 Principle of KPLS-WNN fault diagnosis
4 实验仿真
实验环境:Pentium IV 2.4 GHz CPU,2GB DDR内存,80GB + 7200 转硬盘;Windows XP操作系统。实验中,模拟电路的故障样本采集采用ORCAD 10.5软件中的Capture CIS模块来完成;所涉及算法均采用MATLAB软件编程并调试运行。
4.1 样本集构造
本文采用Sallen-Key带通滤波器作为模拟电路故障诊断对象,电路中的各元器件标称值如图4所示[17]。设电阻的容差为5%,电容的容差为10%,且输出端Out为唯一可测试节点。通过综合比较各元件对输出波形影响的灵敏度,可确定故障集包含8种故障模式,即R2-,R2+,R3-,R3+,C1-,C1+,C2-和C2+,其中符号-和+分别表示偏小软故障和偏大软故障,偏差标称值都为±50%,再加上正常模式总共9种模式。
采用软件PSPICE对每种模式进行交流小信号扫描分析(AC Sweep),设输入Vin为幅值1 V的交流电压信号,扫描频率为1 kHz~1 MHz,可得到各模式下的输出波形,并进行比较分析,可发现波形的9个特征参数变化存在明显差异,即分别为:电压最大值,低通截止频率(3 dB),高通截止频率(3 dB),带宽(3 dB),带宽(4 dB),中心频率(3 dB),Q(3 dB),Q(4 dB),Q(5 dB),如图5所示。基于此,可选取这9个波形特征参数作为各个模式的特征输入向量。对每种模式进行50次蒙特卡洛分析,由此可获得450(即50×9) 个特征输入向量,对数据归一化处理后,从中随机抽取40%数据的作为训练样本集,余下60%作为测试样本集。此外,故障类型的期望输出向量可由“0-l”法来描述,如R3+模式可表示为[1 1 1 0 1 1 1 1]。
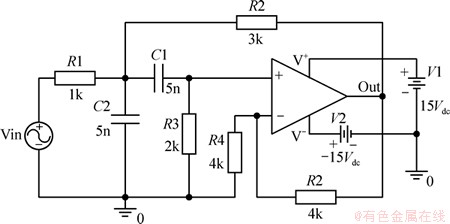
图4 Sallen-Key带通滤波器
Fig. 4 Sallen-Key band pass filter
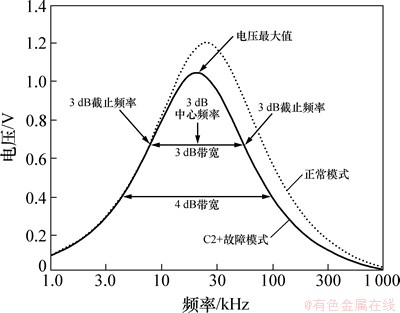
图5 波形特征参数提取示意图
Fig. 5 Diagram of waveform feature parameters extraction
4.2 实验分析
为便于比较,实验分别采用WNN,PLS-WNN和KPLS-WNN算法对被测电路进行故障诊断测试。所涉及WNN的隐节点,根据经验公式 (d为[1,10]区间的整数) 都取为20,参数wji,wkj,aj和bj的初始值取[-0.5,0.5]内随机数,KPLS的核函数取
(d为[1,10]区间的整数) 都取为20,参数wji,wkj,aj和bj的初始值取[-0.5,0.5]内随机数,KPLS的核函数取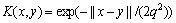 (其中,q为核参数)。实验中,设WNN输出层任意1个节点的实际输出值与期望输出值差值的绝对值大于判定值0.3,则认为诊断错误。
(其中,q为核参数)。实验中,设WNN输出层任意1个节点的实际输出值与期望输出值差值的绝对值大于判定值0.3,则认为诊断错误。
根据前述的KPLS-WNN集成运算过程,对构造的原始样本集进行特征提取,进而利用所得到的特征主元建立WNN故障诊断模型。表1所示为3种算法的建模性能和诊断误差对比。其中:PLS-WNN的主元数选取6时诊断效果最好;而KPLS-WNN为q=0.8,p=5时的诊断效果最好。表2所示为3种模型对各个模式的正确诊断结果。图6所示为3种模型的训练收敛曲线,而图7所示为主元数p和核参数q对KPLS-WNN模型诊断结果。
由表1,表2和图6可以看出:PLS-WNN和KPLS-WNN的训练误差、测试误差和收敛次数都比WNN的小,说明经PLS和KPLS特征提取的WNN模型性能确实优于未提取特征的性能。而相对于PLS-WNN,KPLS-WNN具有更好的训练、测试和收敛效果,其仅仅通过不到300次训练,模型就达到收敛;除R2+,C1-和C1+外,其他模式的诊断正确率为100%,总正确率也达到96.7%,这表明PLS仅局限于提取线性特征。而通过引入核方法,将样本映射到高维特征空间再进行PLS特征提取,能够提取特征空间中包含的高阶非线性特征,并明显提升了WNN的模型性能,进而确立了KPLS-WNN在模拟电路软故障诊断中的优势。而由图7可知:当主元数p分别为5,10,15,20,25,并且核参数q在0.5~1.5区间取值时,所建立的KPLS-WNN模型可取得较为满意的诊断效果,表1中KPLS-WNN的参数设置q=0.8,p=5,也是据此而来,这一特性对于KPLS-WNN的实际推广非常重要。
表1 各模型的训练和测试性能对比
Table 1 Comparison of training and test capability between each model

表2 各模型的正确诊断结果对比
Table 2 Comparison of correct diagnostic results between each model


图6 训练收敛曲线对比
Fig. 6 Comparison of training convergence curves

图7 参数p和q对模型诊断性能的影响
Fig. 7 Effect of parameter p and q on model diagnosis capability
5 结论
(1) PLS-WNN和KPLS-WNN的诊断正确率和收敛特性总体上比WNN的高,说明通过预先特征提取能有效提高WNN的建模性能,从而为改进WNN提供了新思路。
(2) 与PLS-WNN相比,KPLS-WNN的整体性能显著提高,表明PLS仅局限于提取线性特征,而KPLS能够提取特征空间中的高阶非线性特征,从而显著改善了WNN的模型性能。
(3) Sallen-Key带通滤波器的仿真结果表明:使用KPLS-WNN构建故障诊断模型,收敛速度快,诊断准确率高,从而为模拟电路的软故障诊断问题提供了一条新的解决途径,值得深入研究和推广。
(4) 由于KPLS-WNN诊断方法尚处于初步提出和测试阶段,其在模拟电路软故障领域中的应用还有许多亟待解决的问题,下一步研究的问题是:如何准确诊断模拟电路中同时出现的2个或2个以上的软故障。
参考文献:
[1] 谭阳红, 何怡刚. 模拟电路故障诊断的小波方法[J]. 电工技术学报, 2005, 20(8): 89-93.
TAN Yanghong, HE Yigang. Wavelet method of analogue circuits fault diagnosis[J]. Transactions of China Electrotechnical Society, 2005, 20(8): 89-93.
[2] 彭敏放, 何怡刚, 王耀南, 等. 模拟电路的融合智能故障诊断[J]. 中国电机工程学报, 2006, 26(3): 19-24.
PENG Minfang, HE Yigang, WANG Yaonan, et al. Synthetic intelligence based fault diagnosis of analog circuits[J]. Proceed- ings of the CSEE, 2006, 26(3): 19-24.
[3] 金维香, 张颖. 基于Matlab/PSB的电路仿真分析[J]. 长沙电力学院学报, 2004, 19(2): 49-51.
JIN Weixiang, ZHANG Ying. Analysis of circuit simulation based on Matlab/PSB[J]. Journal of Changsha University of Electric Power, 2004, 19(2): 49-51.
[4] Bandler J W, Salama A E. Fault diagnosis of analog circuits[J]. Proc TEEE, 1985, 73(8): 1279-1327.
[5] 祝文姬, 何怡刚. 容差模拟电路软故障诊断的神经网络方法[J]. 电工技术学报, 2009, 24(11): 184-191.
ZHU Wenji, HE Yigang. Neural network based soft fault diagnosis of analog circuits with tolerances[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 184-191.
[6] LIU Meirong, HE Yigong, LI Xiangxin. Fault diagnosis of analog circuits based on CFNN[J]. Advanced Engineering Forum, 2012, 6/7: 1045-1050.
[7] 赵光权, 彭喜元, 马勋亮. 基于微分进化神经网络的模拟电路故障诊断 [J]. 测试技术学报, 2012(1): 88-92.
ZHAO Guangquan, PENG Xiyuan, MA Xunliang. Analog circuit fault diagnosis using differential evolution neural network[J]. Journal of Test and Measurement Technology, 2012(1): 88-92.
[8] 郭珂, 伞冶, 朱亦. 基于PSO-RBF神经网络的模拟电路故障诊断研究[J]. 电子设计工程, 2011, 19(24): 17-20, 23.
GUO Ke, SAN Ye,ZHU Yi. Research on analog circuit fault diagnosis based on PSO-RBF neural networks[J]. Electronic Design Engineering, 2011, 19(24): 17-20, 23.
[9] Zhang Q H, Benveniste A. Wavelet network[J]. IEEE Trans- actions on Neural Networks, 1992, 3(6): 889-898.
[10] Zhang Q H. Using wavelet network in nonparametric estimation[J]. IEEE Transactions on Neural Networks, 1997, 8(2): 227-236.
[11] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1999: 138-149.
[12] Vapnik V N. An overview of statistical learning theory[J]. IEEE Transaction on Neural Networks, 1999, 10(5): 988-999.
[13]  G, et a1. An introduction to kernel based learning algorithms[J]. IEEE Transactions on Neural Networks, 2001, 12(2): 181-202.
G, et a1. An introduction to kernel based learning algorithms[J]. IEEE Transactions on Neural Networks, 2001, 12(2): 181-202.
[14] Suykens J K A, Gestel T V, Brabanter J D, et al. Least squares support vector machines[M]. Singapore: World Scientific Publishing Company, 2002.
[15] Rosipal R, Leonard J T. Kernel partial least squares regression in reproducing kernel hilbert space[J]. Journal of Machine Learning Research. 2001, 2(6): 97-123.
[16] 李金屏, 王风涛, 杨波. BP小波神经网络快速学习算法研究[J]. 系统工程与电子技术, 2001, 23(8): 72-75.
LI Jinping, WANG Feitong, YANG Bo. Fast training algorithm of BP wavelet neural network[J]. System Engineering and Electronics, 2001, 23(8): 72-75.
[17] 满高华. 基于小波分析和神经网络的模拟电路软故障诊断研究[D]. 南宁: 广西大学电气工程学院, 2009: 35-39.
MAN Gaohua. The research of analog circuit soft fault diagnosis based on wavelet analysis and neural network[D]. Nanning: Guangxi University. College of Electrical Engineering, 2009: 35-39.
(编辑 何运斌)
收稿日期:2013-06-19;修回日期:2013-08-22
基金项目:国防预研基金资助项目(9140A17020307JB3201)
通信作者:丛伟(1973-),女,辽宁铁岭人,博士研究生,从事综合航电、检测技术研究;电话:029-84787656;E-mail:kgy_congwei@163.com