A novel sparse filtering approach based on time-frequency feature extraction and softmax regression for intelligent fault diagnosis under different speeds
来源期刊:中南大学学报(英文版)2019年第6期
论文作者:陈怀海 张忠伟 李舜酩 王金瑞
文章页码:1607 - 1618
Key words:intelligent fault diagnosis; short time Fourier transform; sparse filtering; softmax regression
Abstract: Modern agricultural mechanization has put forward higher requirements for the intelligent defect diagnosis. However, the fault features are usually learned and classified under all speeds without considering the effects of speed fluctuation. To overcome this deficiency, a novel intelligent defect detection framework based on time-frequency transformation is presented in this work. In the framework, the samples under one speed are employed for training sparse filtering model, and the remaining samples under different speeds are adopted for testing the effectiveness. Our proposed approach contains two stages: 1) the time-frequency domain signals are acquired from the mechanical raw vibration data by the short time Fourier transform algorithm, and then the defect features are extracted from time-frequency domain signals by sparse filtering algorithm; 2) different defect types are classified by the softmax regression using the defect features. The proposed approach can be employed to mine available fault characteristics adaptively and is an effective intelligent method for fault detection of agricultural equipment. The fault detection performances confirm that our approach not only owns strong ability for fault classification under different speeds, but also obtains higher identification accuracy than the other methods.
Cite this article as: ZHANG Zhong-wei, CHEN Huai-hai, LI Shun-ming, WANG Jin-rui. A novel sparse filtering approach based on time-frequency feature extraction and softmax regression for intelligent fault diagnosis under different speeds [J]. Journal of Central South University, 2019, 26(6): 1607-1618. DOI: https://doi.org/10.1007/s11771- 019-4116-5.

ARTICLE
J. Cent. South Univ. (2019) 26: 1607-1618
DOI: https://doi.org/10.1007/s11771-019-4116-5
ZHANG Zhong-wei(张忠伟)1, CHEN Huai-hai(陈怀海)1, LI Shun-ming(李舜酩)2, WANG Jin-rui(王金瑞)2
1. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
2. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Modern agricultural mechanization has put forward higher requirements for the intelligent defect diagnosis. However, the fault features are usually learned and classified under all speeds without considering the effects of speed fluctuation. To overcome this deficiency, a novel intelligent defect detection framework based on time-frequency transformation is presented in this work. In the framework, the samples under one speed are employed for training sparse filtering model, and the remaining samples under different speeds are adopted for testing the effectiveness. Our proposed approach contains two stages: 1) the time-frequency domain signals are acquired from the mechanical raw vibration data by the short time Fourier transform algorithm, and then the defect features are extracted from time-frequency domain signals by sparse filtering algorithm; 2) different defect types are classified by the softmax regression using the defect features. The proposed approach can be employed to mine available fault characteristics adaptively and is an effective intelligent method for fault detection of agricultural equipment. The fault detection performances confirm that our approach not only owns strong ability for fault classification under different speeds, but also obtains higher identification accuracy than the other methods.
Key words: intelligent fault diagnosis; short time Fourier transform; sparse filtering; softmax regression
Cite this article as: ZHANG Zhong-wei, CHEN Huai-hai, LI Shun-ming, WANG Jin-rui. A novel sparse filtering approach based on time-frequency feature extraction and softmax regression for intelligent fault diagnosis under different speeds [J]. Journal of Central South University, 2019, 26(6): 1607-1618. DOI: https://doi.org/10.1007/s11771- 019-4116-5.
1 Introduction
Owing to the rapid enhancement of engineering technology, agricultural mechanization has become the vital feature to modern agriculture. Agricultural machineries usually work in tough environment which may result in higher fault rate compared with the automobiles. Engine is widely used as the key component to provide power for the agricultural machinery. Any defects in engine cause unwanted fatal breakdowns, expensive maintenance costs, and may cause casualties. Thus, any faulty part (e.g., bearings and gears) of the engine needs to be timely identified. As a result, the fault diagnosis of bearings and gears has drawn extensive attention to guarantee the normal operation of the engine [1-4].
The raw vibration data commonly acquired under different cases are employed to the intelligent defect detection approaches to recognize the different fault existences [5]. In general, the learning process of most published intelligent defect detection works contains two stages: feature excavation and distinguishment [6]. However, the original vibration signal measured from machine surface may contain redundant noise. Consequently, extracting the effective features which include the inherent characteristics of the faulty parts for intelligent fault detection is very necessary [7]. In recent years, several signal processing technologies have been successfully employed to get the inherent characteristics from the original data: time-domain processing [8], frequency-domain analysis [9], and time-frequency domain processing, for instance, STFT (short time Fourier transform) and WT (wavelet transform) [10]. In addition, these signals processing technologies also can be combined to extract the features. LI et al [11] extracted representative features from the gearbox vibration measurements by applying time-domain analysis, frequency-domain analysis and wavelet transformation, separately. Then, representative characteristics for different domains are integrated according to a classifier based on support vector. After extracting the meaningful characteristics from the primary data, the classifier such as KNN (k-nearest neighbor) [12], SVM (support vector machine) [13], or softmax regression is chosen to classify the fault patterns.
As a result of the rapid enhancement for the Internet and industries, the amount of primary data acquired has increased in an exponential way. The Big Data era has arrived for the mechanical defect diagnosis [14], which has the properties of large- volume, diversity and high-velocity. Consequently, under the background of mechanical big data, how to rapidly draw the effective characteristics becomes a key research issue.
Nevertheless, the traditional fault diagnosis technique is less effective when analyzing the fault of complex structure, and it heavily relies on the abundant prior experience about signal analysis approaches and detection knowledge. In order to overcome these shortcomings, fault diagnosis has been developed from traditional technology to intelligent technology, such as ANN (artificial neural networks) [15], auto-encoders [16], RBM (restricted Boltzmann machine) [17], and CNN (convolutional neural networks) [18, 19]. JIA et al [20] utilized a five layers SAE-based DNNs framework and applied the frequency-domain data as the input of motor bearing defect detection. LI et al [21] employed a deep random forest for fusing the outputs of the two layers DBMs (deep Boltzmann machines) for gearbox fault diagnosis. Whereas, these intelligent fault diagnosis methods may suffer a weakness, for instance, good detection performance can be gained while the parameters are chosen reasonably. However, the parameters are complex and variable, which is inconvenient to tune.
NGIAM et al [22] proposed a new unsupervised learning algorithm-sparse filtering without building the data distribution model, which was different from other feature learning methods. It was easy to implement because only one parameter (feature dimensions) is required to be adjusted. It made the feature sparse by optimizing a simple cost function based on  2-normal, which was convenient to realization according to a simple MATLAB program. Therefore, sparse filtering is an efficient and simple approach to acquire the fault features. LEI et al [23] has applied the sparse filtering algorithm to fault detection of the motor bearing using the time-domain vibration signal, and obtained relatively higher accuracy.
2-normal, which was convenient to realization according to a simple MATLAB program. Therefore, sparse filtering is an efficient and simple approach to acquire the fault features. LEI et al [23] has applied the sparse filtering algorithm to fault detection of the motor bearing using the time-domain vibration signal, and obtained relatively higher accuracy.
In fact, many intelligent fault detection approaches perform well only based on a common precondition: the training and testing samples obey the same data distribution. Nevertheless, in the real application, the vibration raw data are usually acquired under different work conditions run counter to the above assumption and lead to large distribution divergences, which may cause the performances of intelligent fault diagnosis methods drop dramatically. To avoid this shortcoming, we might wish to refine a new detection model trained in one condition for other working conditions.
In this work, the defect detection of the gears and bearings are carried out separately to confirm the effectiveness of STFT based sparse filtering approach. The time-frequency domain representation (e.g., power spectrum) is simpler than the time-domain signal and the energy or intensity of the time-frequency domain signal can be indicated on both time-domain and frequency- domain simultaneously which makes the features of data more comprehensive. In particular, time- frequency transform owns its unique ability when dealing with non-stationary signals and classifying health conditions under different speeds. Consequently, the raw vibration signals are firstly preprocessed by STFT. Then, the output of the STFT preprocessing is adopted to extract the fault features by sparse filtering. Finally, the softmax regression algorithm is utilized as a classifier for distinguishing the mechanical fault types according to the learned features. The remainder of our paper is described as follows: briefly introductions for the theory of time-frequency transform, sparse filtering and softmax regression algorithm are included in Section 2; Section 3 mainly shows the process and framework of the proposed approach. For Section 4, firstly, the effectiveness of our method is verified by fault diagnosis of a bearing dataset, and then the robustness of the proposed approach is validated by defect diagnosis of a gear dataset. Finally, the conclusions are discussed in Section 5.
2 Related works
2.1 Time-frequency transform
In many practical applications, the vibration signal is non-stationary because of its time-varying characteristics. The typical time-frequency representations mainly contain STFT, WT (wavelet transform), S transform and Gabor expansion [24].
The basic idea of STFT: 1) the window function is employed to intercept the signal; 2) the Fourier transform is utilized for analyzing the original signal in the window to determine the frequency at that moment; 3) the relation between frequency and time is gained by moving the window function along the signal, finally, the time frequency distribution is obtained [25]. This process is based on a hypothesis that the signal is stable in the window. The definition of STFT is as follows.
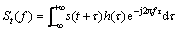 (1)
(1)
where h(τ) denotes the window function, and different window functions are utilized to get different short time spectra.
2.2 Sparse filtering
The traditional unsupervised feature learning methods [26, 27] need to adjust various parameters which make the features difficult to learn. Sparse filtering is a novel feature learning method which aims to obtain the sparse characteristics based on the weight maxtrix by an unsupervised method [22]. It directly analyzes the distribution of features by optimizing the activation value of  2-normalized features and the sparse constraint of
2-normalized features and the sparse constraint of  1-norm, and only one parameter (the number of features) is required to be tuned. Sparse filtering can satisfy three conditions of feature optimization [28-30]:1) population sparsity; 2) lifetime sparsity; 3) large dispersivity. The architecture of sparse filtering is depicted in Figure 1.
1-norm, and only one parameter (the number of features) is required to be tuned. Sparse filtering can satisfy three conditions of feature optimization [28-30]:1) population sparsity; 2) lifetime sparsity; 3) large dispersivity. The architecture of sparse filtering is depicted in Figure 1.
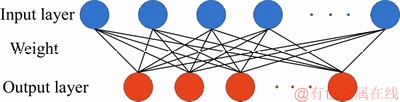
Figure 1 Architecture of sparse filtering
The sparse filtering algorithm is achieved as below:
1) Time-frequency domain data are extracted from several fault types and composed the sample matrix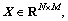 where N represents vector dimension, M denotes the number of samples, the feature matrix F corresponds to X is
where N represents vector dimension, M denotes the number of samples, the feature matrix F corresponds to X is 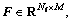 where each column of F represents Nf dimension feature vector, and its principle is shown as follows:
where each column of F represents Nf dimension feature vector, and its principle is shown as follows:
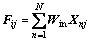 (2)
(2)
where 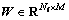 denotes the weight parameter.
denotes the weight parameter.
2) The matrix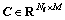 is obtained by normalizing every row of
is obtained by normalizing every row of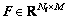 according to its
according to its  2-norm.
2-norm.
3) The matrix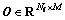 is got by normalizing each column of the feature matrix based on the
is got by normalizing each column of the feature matrix based on the  2-norm to restrict the characteristics on the unit
2-norm to restrict the characteristics on the unit  2-sphere.
2-sphere.
4) The target function is minimized, which is shown as follows.
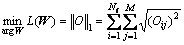 (3)
(3)
where partial derivative of L(W) corresponding to W can be obtained from Eq. (4):
 (4)
(4)
where

 (5)
(5)
After the values of X and W are given, the weight matrix Wout which is required to sparse filtering can be obtained from Eqs. (3) and (4) by L-BFGS algorithm [31].
2.3 Softmax regression
The softmax regression algorithm [32] can be employed to solve the multiple regression problems. It is widely used in the supervised learning part of the depth learning research as a classifier. Assume that a training set of the softmax regression contains m samples, i.e., {(x1, y1), …, (xm, ym)}, where x denotes the input feature, the label set is 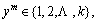 and k refers to the amount of categories. Given a input feature x, the probability p(y=j|x) of every category j is estimated using the hypothesis function, that is, the probability of each classification result of x is estimated, and the maximum probability category is the output value. The probability p(yi=j|x) of every category j is obtained by the hypothesis function. Accordingly, the result hθ(xi) consists of a k-dimensional column vector:
and k refers to the amount of categories. Given a input feature x, the probability p(y=j|x) of every category j is estimated using the hypothesis function, that is, the probability of each classification result of x is estimated, and the maximum probability category is the output value. The probability p(yi=j|x) of every category j is obtained by the hypothesis function. Accordingly, the result hθ(xi) consists of a k-dimensional column vector:
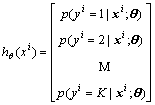
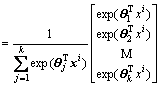 (6)
(6)
where θ1, θ2, …, θk refer to the parameters for the model, which can be represented by the matrix θ=[θ1, θ2, …, θk]T, p(yi=j|xi; θ) represents the probability that category j contains the sample xi.
θ can be calculated by minimizing the loss function of softmax regression, and thus predicting the category of a new sample. The objective function of the softmax regression algorithm can be obtained from Eq. (7):
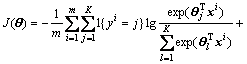
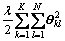 (7)
(7)
where m denotes samples number, k represents the categories number, λ refers to the term of weight decay, 1{·} denotes an indicative function, namely 1{true}=1, 1{false}=0.
For minimizing the J(θ), a gradient descent algorithm is generally employed for solving this issue. The partial derivative function of J(θ) is computed as follows:
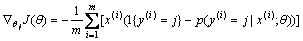 (8)
(8)
where the value of j=1, 2, …, k, 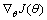 denotes a vector that indicates the partial derivative of J(θ) with respect to θj.
denotes a vector that indicates the partial derivative of J(θ) with respect to θj.
3 Proposed framework
The samples are commonly utilized to train the learned features in sparse filtering without considering the effects of speed fluctuations. However, in the real word, the vibration raw signals are usually acquired under different speeds, and the speed fluctuations cannot be ignored. Correspondingly, for the sake of simulating the case of speed fluctuations, the samples under one speed are employed for training the sparse filtering, and the samples under the rest speeds are selected to test the performance. The implementation steps for the proposed framework are introduced as follows:
1) A speed is randomly selected, and the samples under this speed are adopted as the training samples.
2) The raw vibration signals representing the various fault types are pretreated by STFT to obtain the time-frequency signals which compose the training set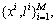 where M denotes the samples number,
where M denotes the samples number,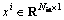 denotes the ith sample including Nin data points, li denotes the label of xi. The sample set is written as a matrix form
denotes the ith sample including Nin data points, li denotes the label of xi. The sample set is written as a matrix form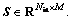
3) The matrix S is employed to train the sparse filtering model to get the weight matrix W. The learned features 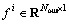 can be obtained from Eq. (2), and thus these learned features compose the feature dataset
can be obtained from Eq. (2), and thus these learned features compose the feature dataset 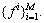
4) The label set 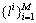 is combined with the feature dataset
is combined with the feature dataset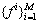 to build the softmax regression model. Then the softmax regression model is tested using the rest samples.
to build the softmax regression model. Then the softmax regression model is tested using the rest samples.
In brief, firstly, the time-frequency domain signal of samples under the selected speed is obtained by time-frequency transform. Then, these samples are employed for training the sparse filtering model to get the learned features. Thirdly, the fault types under the other speeds are classified by the softmax regression classifier according to the learned characteristics. The procedure of our approach is displayed in Figure 2.
4 Fault detection with proposed approach
4.1 Case 1: Bearing defect diagnosis
4.1.1 Presentation of experimental data
The vibration signals of bearings adopted in this case were offered by Case Western Reserve University, USA. The vibration signal of bearings assembled on the fan end and the driving end were measured by the vibration accelerometer. Note that the sampling frequency was set as 12 kHz. The bearing vibration data of the driving end were utilized in this case, which was measured under four kinds of conditions, i.e., 1) normal condition; 2) outer ring defect (OD); 3) inner ring defect (ID); 4) roller defect (RD). Besides, the vibration data of three distinct defect sizes (0.18, 0.36 and 0.54 mm) were separately collected. Furthermore, the vibration test data of bearings were obtained under four distinct loads: 0, 745.7, 1491.4 and 2237.1 W. These four kinds of loads corresponded to different speeds (1797, 1772, 1750, 1730 r/min), respectively.
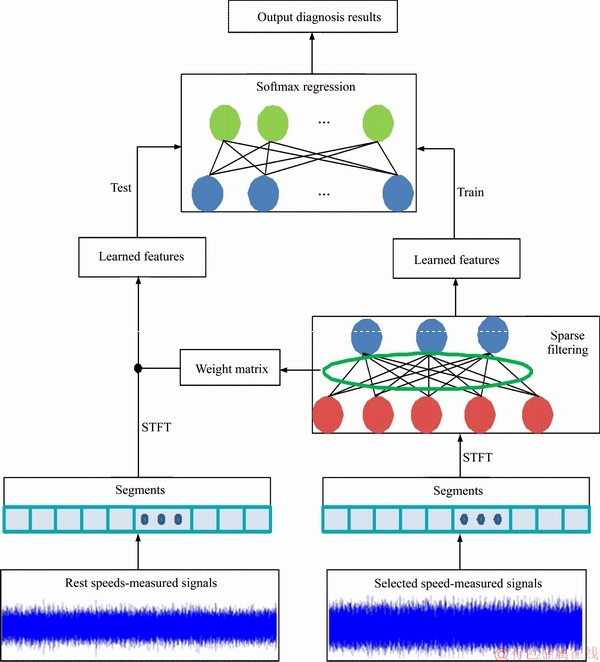
Figure 2 Strucure of proposed approach
The motor bearing dataset contained the vibration signals at all speeds, which was adopted for validating the effectiveness of the proposed approach. The same health conditions under four different speeds were considered as one class. Thus, ten types of faults were obtained. Each fault types of one rotating speed contained 100 samples and every sample included 1200 points. As a result, the bearing dataset totally consisted of 4000 samples, and there were 1000 samples under each speed.
4.1.2 Diagnosis results
In this section, the effectiveness of the proposed approach was validated by classifying the faults of bearing dataset. The samples under a randomly selected speed were chosen for training and the rest samples under the other speeds were used for testing. For decreasing the randomness, 15 trials of the experiment were carried out.
Firstly, the time-domain data was transformed to time-frequency signal using STFT, as displayed in Figure 3. In the process of STFT, Hamming window function was adopted. The length coefficient of the window was chosen as 0.03, and the overlapping rate between frames was adopted as 75%. The number of data points utilized for short time Fourier transform (STFT) was fixed as 512, and the PSD matrix was 257×10. Then, the PSD matrix was processed by feature averaging of time-domain. The training set 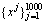 consisted of samples under the training speed, where
consisted of samples under the training speed, where 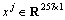 was the jth part including 257 datapoints. Then, the training samples were adopted for training the sparse filtering model. The input dimension of sparse filtering model was determined by PSD matrix dimension, in addition, the output dimension was the same as the input dimension. Therefore, the input and output dimensions (Nin and Nout) of sparse filtering were both set to 257. Subsequently, the matrix W was gained by training the sparse filtering algorithm. The remainder samples were employed to obtain the fault characteristics by Eq. (2). Then, a 257 dimension vector was gained for every test sample. In the final step, softmax regression was employed to predict the fault types of the test samples. Note that the training samples and the test samples were labeled separately, and the weight parameter λ was chosen as λ=10-5. The training samples were adopted for training the softmax regression classifier, and the rest samples were utilized for testing, the defect diagnosis accuracies are depicted in Figure 3. As we can see, the diagnosis accuracies of 15 trials obtained by the proposed method are in the range of 97.73%-99.73%. In addition, the average defect diagnosis accuracy is 99.01%. Therefore, the diagnosis accuracy is relatively high and stable.
was the jth part including 257 datapoints. Then, the training samples were adopted for training the sparse filtering model. The input dimension of sparse filtering model was determined by PSD matrix dimension, in addition, the output dimension was the same as the input dimension. Therefore, the input and output dimensions (Nin and Nout) of sparse filtering were both set to 257. Subsequently, the matrix W was gained by training the sparse filtering algorithm. The remainder samples were employed to obtain the fault characteristics by Eq. (2). Then, a 257 dimension vector was gained for every test sample. In the final step, softmax regression was employed to predict the fault types of the test samples. Note that the training samples and the test samples were labeled separately, and the weight parameter λ was chosen as λ=10-5. The training samples were adopted for training the softmax regression classifier, and the rest samples were utilized for testing, the defect diagnosis accuracies are depicted in Figure 3. As we can see, the diagnosis accuracies of 15 trials obtained by the proposed method are in the range of 97.73%-99.73%. In addition, the average defect diagnosis accuracy is 99.01%. Therefore, the diagnosis accuracy is relatively high and stable.
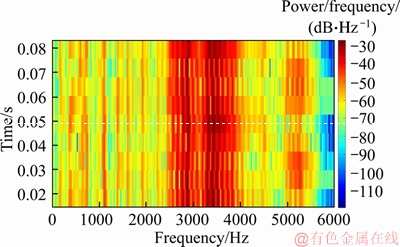
Figure 3 Time-frequency graph of bearing vibration signals
4.1.3 Comparison analysis
The superiority of the proposed approach is validated by comparing it with several successful approaches:
1) Time-domain sparse filtering;
2) Frequency-domain sparse filtering;
3) Time-frequency domain (based on WT) sparse filtering;
4) Time-frequency domain stacked auto-encoders (SAEs).
For the time-domain sparse filtering, the input and output dimensions of sparse filtering were both selected as 100, and the weight parameter λ was chosen as λ=10-5. We randomly chose one speed, and the samples under this speed were employed as training samples. Specially, 50000 segments were obtained by segmenting the training dataset for training sparse filtering model, and the remainder samples were selected to test. As we can see from Figure 5, the diagnosis accuracies obtained by time- domian method are in the range of 88.29%-94.11% and the average defect diagnosis accuracy rate is 92.13%. In a word, the diagnosis accuracies are lower and less stable compared to the proposed method.
For the frequency-domain sparse filtering, the Fourier coefficients were obtained by implementing FFT on every sample. Then, the samples under one randomly selected speed were employed to train the sparse filtering model. Specifically, these samples were employed to compose the training set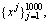 where
where 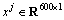 was the jth segment containing 600 data points. The input and output dimensionality for the sparse filtering model were selected as 600. The rest of the samples under the other three speeds were used for testing. The accuracies of the fault detection are also shown in Figure 5. As we can see from Figure 5, the detection accuracies of the frequency domain method are about 60%. Besides, the accuracies are the lowest compared with the other two methods.
was the jth segment containing 600 data points. The input and output dimensionality for the sparse filtering model were selected as 600. The rest of the samples under the other three speeds were used for testing. The accuracies of the fault detection are also shown in Figure 5. As we can see from Figure 5, the detection accuracies of the frequency domain method are about 60%. Besides, the accuracies are the lowest compared with the other two methods.
For the time-frequency domain (based on WT) sparse filtering, the wavelet transform (WT) was adopted for preprocessing the original vibration data. During the process of WT, the complex wavelet was selected. The bandwidth parameter and the central frequency of complex wavelet were all chosen as 4 which could be represented by ‘cmor4-4’ in the wavelet toolbox of MATLAB. In addition, the length of scale was adopted as 256. The result of the WT processing was a two-dimensional matrix with a size of 256×1200, and then, the matrix was processed by feature averaging of time-domain. The rest of steps for the time-frequency domain (based on WT) sparse filtering were the same as the proposed method. As depicted in Figure 5, the average classification accuracy of the WT based sparse filtering algorithm is 91.08%, which is 7.93% less than our model. In addition, the average computation time of the time-frequency domain (based on WT) sparse filtering is 249.3 s, by contrast, the average computation time of our approach is 14.3 s. Consequently, comparing with the wavelet transform (WT), the STFT algorithm applied in the proposed approach can get higher detection accuracy and running efficiency.
For the time-frequency domain stacked autoencoders (SAEs), the collected raw vibration data was first preprocessed by STFT and the parameter settings of STFT were the same to the proposed method. Then, SAEs was adopted for extracting the fault characteristics. Two layers DNNs framework was employed and the neuron number of its input layer was the same as the samples dimensionality. The neuron number of the hidden layer was chosen as 100. The neuron number for the output layer was the same as the counts of defect types. In addition, the training epoch was fixed as 100, the batch size was 50 and the learning rate was set to 0.05. Finally, the softmax regression was utilized as a classifier to distinguish the health states. The experimental results of the time-frequency domain stacked autoencoders (SAEs) are shown in Figure 5, it is noticed that the average detection accuracy rate of the STFT based SAEs method is 94.0%, which is 5.01% less than the proposed model. Thus, it indicates that the proposed method indeed has the obvious superiority to extract the representative fault characteristics from original vibration data of bearing and is more robust than the time-frequency domain SAEs.
In order to research which types of defect features are drawn by time series statistical analysis, FFT and STFT, the distributions of features extracted by these methods are depicted in Figure 4. As we can see from Figure 4, the features extracted by STFT perform more evident and divisible than those acquired by the other two approaches. As a direct result, the features extracted by STFT contain more representative information and are easier to discriminate. Furthermore, STFT performs well in mining the representative fault characteristics from the time-varying original vibration signal which are extracted from non-stationary system. Thus, STFT approach can be utilized for acquiring comparatively high resolution and robust characteristics from the measured dataset.
To further show the diagnosis information clearly, the confusion matrix of our method is displayed in Figure 6. As we can see from Figure 6, there are 300 samples for each fault type, and three samples of the Type-2 are misclassified as the Type-3. Besides, one sample of the Type-3, Type-4 and Type-6 is misclassified as the Type-4, Type-8 and Type-10, respectively. A possible reason for this phenomenon is that the features of Type-2 and Type-3 are very close, as a result, more samples are misclassified. In order to validate that the proposed approach can extract representative characteristics adaptively, t-SNE algorithm [33] is adopted for converting the 257 dimensionality vector into a 3 dimensionality map. The fault detection results of bearing dataset are depicted in Figure 7. As can be seen from Figure 7, most characteristics of the identical fault type under different speeds are assembled in the corresponding group and each group is separated from each other.
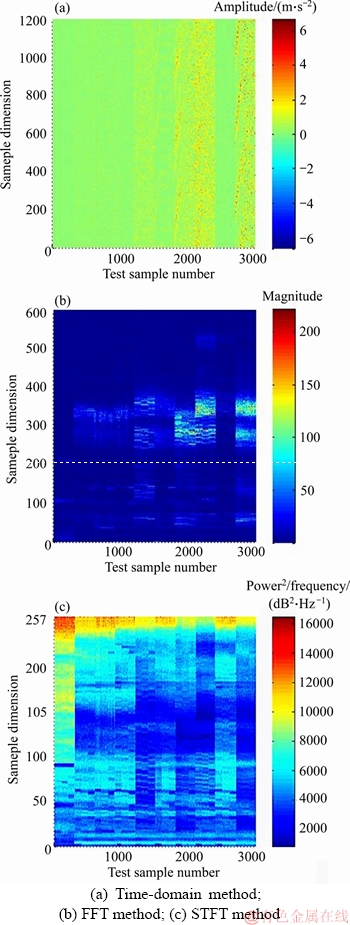
Figure 4 Visualization of features extracted by distinct domain analysis approaches:
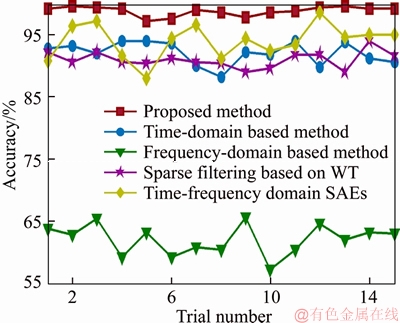
Figure 5 Detection performances of brearing by different methods
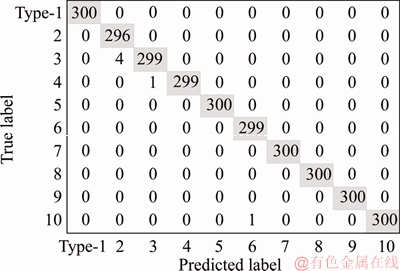
Figure 6 Confusion matrix of bearing dataset
The speed fluctuations could alter the amplitude and frequency of features to bring difficulties for fault diagnosis. Comparing with the time-domain and frequency-domain methods, the superiority of the time-frequency transform is dealing with the unstable signal. Thus its accuracy of fault diagnosis under different speeds is relatively higher. For illustrating the validity and robustness of the proposed approach, a gear defect detection experiment with different speeds is presented in the next section.
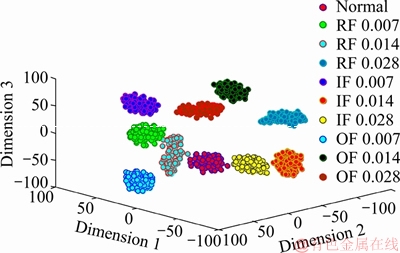
Figure 7 Visualization maps based on learned characteristics
4.2 Case 2: Gear fault diagnosis
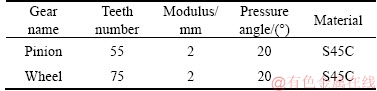
The general gear failures mainly contain pitting corrosion, teeth breakage, wear failure, and compound faults. It is essential for the security of agricultural machinery to diagnose the gear failures accurately [34]. In this part, the effectiveness and robustness of our method was testified by the gear fault detection under distinct speeds. The gearbox test bench employed to acquire original gear dataset is shown in Figure 8. As we can see from Figure 8, the test bench was composed of a gearbox, agricultural machinery engine, a bearing seat, a flexible jointer, the base and so on. The agricultural machinery engine was utilized for controlling the gearbox speed. There were two gears assembled in the gearbox. The parameters of these gears are displayed in Table 1.

Figure 8 Gearbox test bench
Table 1 Parameters of gears
Five kinds of health states, i.e. , the normal gear, compound defect of gearwheel pitting corrosion and pinion wear failure, gearwheel pitting corrosion, compound defect of gearwheel teeth breakage and pinion wear failure, pinion wear failure were included in gear dataset. In addition, the five kinds of health states mentioned above were named as Type-1 to Type-5 in sequence. The speeds for distinct health states are displayed in Table 2. As we can see from Table 2, the data of these gear health states were collected under three distinct speeds, and speed 1, speed 2 and speed 3 denote the rotating speeds controlled by load 149.14, 74.57 and 37.29 W, respectively. It should be pointed out that, the speed of each heath state was distinct under the same case. The details of time-domain under different speeds of the fault Type-4 are displayed in Figure 9. As we can see from Figure 9, the amplitudes of time-domain waveform and spectrum under different speeds are different from each other which bring difficulties to defect detection. The test signals were collected by piezoelectric accelerometer which was installed on the gearbox housing. In addition, the sampling rate was selected as 5120 Hz. Each fault type contained 100 samples, and each sample consisted of 1050 data points. Note that these samples were obtained in an overlapped manner. In the process of time- frequency transform, the Hamming window function was adopted. Specially, the length coefficient of the window was selected as 0.07, and the overlapping rate between frames was 50%. One speed was chosen in a random way, and the samples under this speed were selected to compose the training set 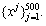 These samples were adopted for training the sparse filtering algorithm while the samples under the other two speeds were utilized for testing. The input and output dimension (Nin and Nout) of sparse filtering model were chosen as 257. The training and test accuracies are depicted in Figure 10. It is worth noting that the training data are the same as the test data during the process of obtaining the training accuracy. As we can see from Figure 10, the average training and test accuracies are 100% and 99.81%, respectively. For the testing accuracy, the samples under a certain speed were adopted for training the sparse filtering algorithm, but the actual application in defect detection was to recognize the testing data drawn under the other two speeds. Although the defect diameter and types are not changed, the divergences of distribution between training and testing dataset alter with the operating conditions. As a direct result, high training accuracy can be achieved while the testing accuracy performs poorly and unstable. This phenomenon results from the distribution differences under different speeds, since features obtained under one speed can not represent for the other speeds. The diagnosis accuracies are relatively high and stable, which indicates that the proposed method owns strong robustness for the case that the speed fluctuations exist among each type of fault.
These samples were adopted for training the sparse filtering algorithm while the samples under the other two speeds were utilized for testing. The input and output dimension (Nin and Nout) of sparse filtering model were chosen as 257. The training and test accuracies are depicted in Figure 10. It is worth noting that the training data are the same as the test data during the process of obtaining the training accuracy. As we can see from Figure 10, the average training and test accuracies are 100% and 99.81%, respectively. For the testing accuracy, the samples under a certain speed were adopted for training the sparse filtering algorithm, but the actual application in defect detection was to recognize the testing data drawn under the other two speeds. Although the defect diameter and types are not changed, the divergences of distribution between training and testing dataset alter with the operating conditions. As a direct result, high training accuracy can be achieved while the testing accuracy performs poorly and unstable. This phenomenon results from the distribution differences under different speeds, since features obtained under one speed can not represent for the other speeds. The diagnosis accuracies are relatively high and stable, which indicates that the proposed method owns strong robustness for the case that the speed fluctuations exist among each type of fault.
Table 2 Speeds for distinct defect types
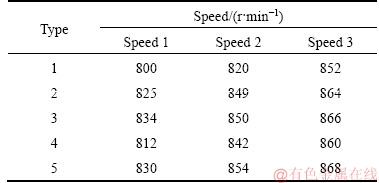
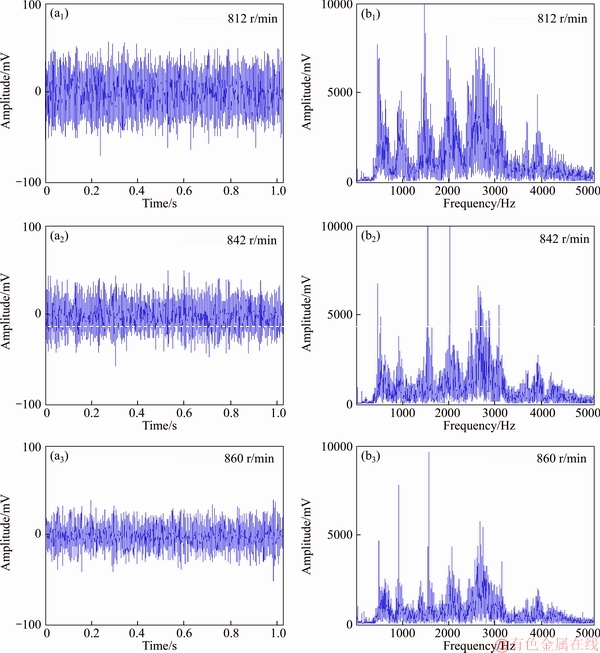
Figure 9 Comparison of time-domain waveform (a) and spectrum under different speeds (b) of Type-4
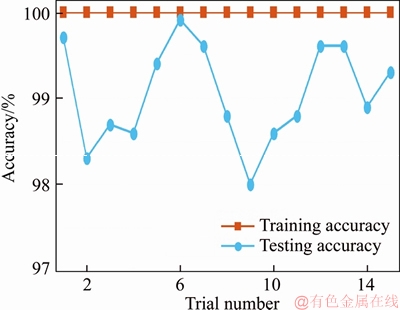
Figure 10 Detection performances of 15 trials of gear by proposed approach
5 Conclusions
A novel sparse filtering approach based on time-frequency feature extraction is presented. In addition, bearings and gears fault diagnosis experiments under different speeds are carried out, respectively. Firstly, the sparse filtering approach is employed for learning the characteristics adaptively. Then, a classifier based on softmax regression algorithm is utilized for identifying the learned fault features. A gear and bearing datasets are adopted for testifying the validity of our approach. The conclusions can be summarized as follows:
1) Robust characteristics can be effectually drawn by the proposed approach from the mechanical fault data of the bearing and gear, and the high accuracy can be obtained for the fault classification under different speeds.
2) The contrasting results with the time- domain based and frequency-domain based mechanical fault detection approaches illustrate that our approach has better robustness and can acquire higher accuracy.
3) For fault diagnosis under different speeds, the proposed method owns its unique superiority. The proposed method could be a validate intelligent approach for defect detection of agricultural machinery due to its less need of human labor or prior knowledge of the data.
References
[1] HE Zheng-jia, CHEN Jin, WANG Tai-yong, CHU Fu-lei. Theory and application of mechanical fault diagnosis [M]. Beijing: Higher Education Press, 2010. (in Chinese)
[2] ZHONG Bing-lin, HUANG Ren. Mechanical fault diagnosis (the third edition) [M]. Beijing: Machinery Industry Press, 2006. (in Chinese)
[3] ZHU Zhong-kui. Research on the application of wavelet analysis in automotive gear transmission fault diagnosis [D]. Hefei: HeFei University of Technology, 2002. DOI: 10.7666/d.y446917. (in Chinese)
[4] JIAO Xin-tao. The wavelet analysis and its application in fault diagnosis of gear box [D]. Guangzhou: South China University of Technology, 2014. DOI: 10.3969/j.issn.1000- 3835.2005.05.030. (in Chinese)
[5] PRIETO M D, CIRRINCIONE G, ESPINOSA A G, ORTEGA J A, HENAO H. Bearing fault detection by a novel condition-monitoring scheme based on statistical-time features and neural networks [J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 3398-3407. DOI: 10. 1109/TIE.2012.2219838.
[6] LI Yong-bo, XU Min-qiang, WANG Ri-xin, HUANG Wen-hu. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree [J]. Measurement, 2016, 77: 80-94. DOI: https://doi.org/10.1016/j.measurement.2015. 08.034.
[7] ZHANG Wei, PENG Gao-liang, LI Chuan-hao, CHEN Yuan-hang, ZHANG Zhu-jun. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals [J]. Sensors, 2017, 17(2): 425-446. DOI: 10.3390/s17020425.
[8] WANG Xiang, ZHENG Yuan, ZHAO Zhen-zhou, WANG Jin-ping. Bearing fault diagnosis based on statistical locally linear embedding [J]. Sensors, 2015, 15(7): 16225-16247. DOI: 10.3390/s150716225.
[9] JOANNIN C, CHOUVION B, THOUVEREZ E, OUSTY J P, MBAYE M. A nonlinear component mode synthesis met the computation of steady-state vibration in non-conservative systems [J]. Mechanical Systems and Signal Processing, 2017, 83: 75-92. DOI: https://doi.org/10.1016/j.ymssp.2016. 05.044.
[10] LI Chuan, SANCHEZ R V, ZURITA G, LOZADA M C, CABRERA D. Rolling element bearing defect detection using the generalized synchrosqueezing transform guided by time-frequency ridge enhancement [J]. ISA Transactions, 2016, 60: 274-284. DOI: 10.1016/j.isatra.2015.10.014.
[11] LI Chuan, SANCHEZ R V, ZURITA G, CERRADE M, CABRERA D. Multimodal deep support vector classification with homologous features and its application to gearbox fault diagnosis [J]. Neurocomputing, 2015, 168: 119-127. DOI: https://doi.org/10.1016/j.neucom.2015.06.008.
[12] XU Dong-wei, WANG Yong-dong, JIA Li-min, ZHANG gui-jun, GUO hai-feng. Real-time road traffic states estimation based on kernel-KNN matching of road traffic spatial characteristics [J]. Journal of Central South University, 2016, 23: 2453-2464. DOI: 10.1007/s11771-016-3304-9.
[13] WIDODO A, YANG B S. Support vector machine in machine condition monitoring and fault diagnosis [J]. Mechanical Systems and Signal Processing, 2008, 21(6): 2560-2574. DOI: https://doi.org/10.1016/j.ymssp.2006. 12.007.
[14] SINHA J K, ELBHBAH K. A future possibility of vibration based condition monitoring of rotating machines[J]. Mechanical Systems and Signal Processing, 3013, 34(1, 2): 231-240. DOI: https://doi.org/10.1016/j.ymssp.2012.07.001.
[15] PAYA B A, ESAT II. Artificial neural networks based fault diagnosis of rotating machinery using wavelet transforms as a preprocessor [J]. Mech Syst Signal Process, 2010, 11(5): 751-765. DOI: https://doi.org/10.1006/mssp.1997. 0090.
[16] VERMA N K, GUPTA V K, SHARMA M. Intelligent condition based monitoring of rotating machines using sparse auto-encoders [J]. Prognostics and Health Management, IEEE, 2013, 7789(4): 1-7. DOI: 10.1109/ ICPHM.2013. 6621447.
[17] TAMILSELVAN P, WANG Ping-feng. Failure diagnosis using deep belief learning based health state classification [J]. Reliability Engineering & System Safety, 2013, 115(7): 124-135. DOI: https://doi.org/10.1016/j.ress.2013.02.022.
[18] GUO Xiao-jie, CHEN Liang, SHEN Chang-qing. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis [J]. Measurement, 2016, 93: 490-502. DOI: https://doi.org/10.1016/j. measurement.2016.07.054.
[19] JANSSENS O, SLAVKOVIKJ V, VERVISCH B, STOCKMAN K, LOCCUFIER M, VERSTOCKT S. Convolutional neural network based fault detection for rotating machinery [J]. Journal of Sound and Vibration, 2016, 377: 331-345. DOI: https://doi.org/10.1016/j.jsv.2016.05. 027.
[20] JIA Feng, LEI Ya-guo, LIN Jing, ZHOU Xin, LU Na. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data [J]. Mechanical Systems and Signal Processing, 2016, 72, 73: 303-315. DOI: https://doi.org/10.1016/ j.ymssp.2015.10.025.
[21] LI Chuan, SANCHEZ R V, ZURITA G, CERRADE M, CABRERA D. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals [J]. Mechanical Systems and Signal Processing, 2016, 76-77: 283-293. DOI: https://doi.org/10.1016/j.ymssp.2016.02.007.
[22] NGIAM J, PANG W K, CHEN Zheng-hao, BHASKAR S, NG A Y. Sparse filtering [J]. Proc Neural Inf Process Syst, 2011, 11: 1125-1133.
[23] LEI Ya-guo, JIA Feng, LIN Jing, XING Sai-bo, DING S X. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data [J]. IEEE Trans Ind Electron, 2016, 63(5): 31-37. DOI: 10.1109/TIE. 2016.2519325.
[24] LOUGHLIN P J. Methods and applications of time- frequency analysis [J]. Asian Pacific Journal of Allergy & Immunology, 2000, 107(5): 30-36. DOI: http://dx.doi.org/ 10.1121/1.429126.
[25] LI Y. Theory and application of time-frequency transform [D]. Xi'an: Northwestern Polytechnical University, 2003. DOI: 10.7666/d.y525922. (in Chinese)
[26] GUO Zhen-yu, WANG Z J. An unsupervised hierarchical feature learning framework for one-shot image recognition [J]. IEEE Transactions on Multimedia, 2013, 15(3): 621-632. DOI: 10.1109/TMM.2012.2234729.
[27] HOU Chen-ping, NIE Fei-ping, LI Xue-dong. Joint embedding learning and sparse regression: a framework for unsupervised feature selection [J]. IEEE Transactions on Cybernetics, 2014, 44(6): 793-804. DOI: 10.1109/TCYB. 2013.2272642.
[28] WORDEN K, STASZEWSKI W J, HENSMAN J J. Natural computing for mechanical systems research: A tutorial overview [J]. Mech Syst Signal Process, 2011, 25(1): 4-111. DOI: https://doi.org/10.1016/j.ymssp.2010.07.013.
[29] SHATNAWI Y, AL-KHASSAWENEH M. Fault diagnosis in internal combustion engines using extension neural network [J]. IEEE Trans Ind Electron, 2014, 61(3): 1434-1443. DOI: 10.1109/tie.2013.2261033.
[30] PRIETO M D, CIRRINCIONE G, ESPINOSA A G, ORTEGA J A, HENAO H. Bearing fault detection by a novel condition-monitoring scheme based on statistical-time features and neural networks [J]. IEEE Trans Ind Electron, 2013, 60(8): 3398-3407. DOI: 10.1109/TIE.2012. 2219838.
[31] LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization [J]. Mathematical Programming, 1989, 45(1-3): 503-528. DOI: https://doi. org/10.1007/BF01589116.
[32] JIANG Ming-yang, LIANG Yan-chun, FENG Xiao-yue. Text classification based on deep belief network and softmax regression [J]. Neural Computing & Applications, 2016: 1-10. DOI: https://doi.org/10.1007/s00521-016-2401-x.
[33] MAATEN L, HINTON G. Visualizing data using t-SNE [J]. Journal of Machine Learning Research, 2008, 620(1): 2579-2605.
[34] JIANG Xing-xing, LI Shun-ming, WANG Yong. A novel method for self-adaptive feature extraction using scaling crossover characteristics of signals and combining with LS-SVM for multi-fault diagnosis of gearbox [J]. Journal of Vibro Engineering, 2015, 17(4): 1861-1878.
(Edited by FANG Jing-hua)
中文导读
一种应用于不同转速下智能故障诊断的基于时频特征提取和softmax回归的稀疏滤波新方法
摘要:现代农业机械化对农机使用过程中的故障诊断提出了更高的要求。然而,故障特征通常是在所有转速下进行学习和分类的,而没有考虑转速波动的影响。为了克服这一缺陷,本文提出了一种基于时频变换的智能故障诊断新框架。在该框架中,一种转速下的样本用来训练稀疏滤波,然后其他转速下的样本用来测试稀疏滤波的性能。本文提出的方法包括两个阶段:1)对机械原始振动数据进行短时傅里叶变换(STFT),得到时频域信号,然后利用稀疏滤波模型从时频信号中提取故障特征。2)基于学习到的故障特征,利用softmax回归对不同的机械健康状况进行分类。提出方法可以用来自适应的提取故障特征,是一种可对农业机械进行有效故障诊断的智能方法。故障诊断结果表明,该方法不仅在不同转速下的故障诊断中下具有较强优势,而且比其他方法具有更高的分类准确率。
关键词:智能故障诊断;短时傅里叶变换;稀疏滤波;softmax回归
Foundation item: Project(51675262) supported by the National Natural Science Foundation of China; Project(2016YFD0700800) supported by the National Key Research and Development Program of China; Project(6140210020102) supported by the Advance Research Field Fund Project of China; Project (NP2018304) supported by the Fundamental Research Funds for the Central Universities, China; Project(2017-IV-0008-0045) supported by the National Science and Technology Major Project
Received date: 2018-01-03; Accepted date: 2018-12-25
Corresponding author: CHEN Huai-hai, PhD, Professor; Tel: +86-13705161051; E-mail: chhnuaa@nuaa.edu.cn; ORCID: 0000-0003- 4693-0775

