参数激励作用下水下悬浮隧道锚索的稳定性研究

苏志彬，孙胜男

(聊城大学 建筑工程学院，山东 聊城，252059)

摘要：为研究水下悬浮隧道锚索在索端参数激励作用下振动的稳定性，建立锚索的参数振动数学方程并用伽辽金法对其进行简化后，采用Lyapunov指数法判断锚索振动的稳定性，分析锚索索端激励幅值、频率和系统阻尼比对锚索振动稳定性的影响。计算结果表明：随着索端激励幅值的增加，不稳定区域逐渐增大，当索端激励频率为锚索固有频率2倍左右时，锚索最易发生失稳，锚索振动系统阻尼比越大，锚索越易趋于稳定状态。

关键词：悬浮隧道；锚索；参数激励；稳定性

中图分类号：U 459.5          文献标志码：A         文章编号：1672-7207(2013)06-2549-05

Stability of submerged floating tunnel tether subjected to parametric excitation

SU Zhibin, SUN Shengnan

(School of Architecture and Civil Engineering, Liaocheng University, Liaocheng 252059, China)

Abstract: To study the vibration stability of submerged floating tunnel tether subjected to parametric excitation, the parametric vibration equation of tether was set up. The equation was simplified by Galerkin method. The vibration stability of tether was judged by Lyapunov exponent method. Effects of excitation amplitude of tether end, frequency and damping ratio on vibration stability of tether were also analyzed. The results show that unstable region expands gradually as the excitation amplitude of tether end increases; when excitation frequency of tether end is twice as that of tether, the tether is easy to be unstable; the tether tends to be stable as the damping ratio of tether increases.

Key words: submerged floating tunnel; tether; parametric excitation; stability

悬浮隧道，也称作阿基米德桥，基于阿基米德浮力理论承受荷载。悬浮隧道由锚固于海床上的锚索支撑，通过水的浮力、自身的重力和锚固力的平衡作用使隧道悬浮在水中适当深度^[1]。悬浮隧道在大跨海域的交通连接上具有独特的优势^[2]，但悬浮隧道所处的复杂环境使得其结构分析、施工及运营不同于传统隧道和桥梁。相对传统隧道而言，悬浮隧道在动力作用下更容易产生振动^[3-5]。锚索作为悬浮隧道的支撑系统，具有阻尼小、密度轻、柔度大的特点，是一种极易发生振动的构件。锚索的振动可分为2类：第一类是荷载引起的振动，譬如海流、涡街等诱发的锚索的振动；第二类是隧道管体振动引起的锚索的振动，这类振动又可再分为由锚索和隧道管体线性耦合引起的振动和参数激励振动^[6]。所谓参数激励振动，是指激励作为参数出现在振动系统中并随时间变化所引起的振动。当参数激励频率和锚索的固有频率成一定倍数关系时，小的激励也会使锚索产生大幅振动^[7]，这种大幅振动有可能使锚索失去稳定。为研究锚索在参数激励作用下的稳定性问题，本文作者将隧道管体对锚索的作用简化为轴向简谐参数激励，建立索端参数激励作用下悬浮隧道锚索的非线性振动方程，采用Lyapunov指数意义下的振动稳定性分析方法，通过对系统最大Lyapunov指数的求解，对锚索的参数振动稳定性进行分析。

1  参数激励系统

建立图1所示坐标系并作如下假定：

(1) 锚索底部与海底铰接，锚索上部与隧道管体铰接。

(2) 由于锚索的抗弯刚度非常小，此处忽略不计；

(3) 锚索的端部激励假设为简谐荷载，其振动方程为：Z=Z_ccos(ω_Tt)。其中：ω_T为索端激励频率；Z_c为索端激励幅值。

(4) 锚索具有一定的垂度，且锚索跨中垂度f与锚索无应力状态的长度L之比小于1/8。假定锚索的初始构形为抛物线，则

               (1)

图1  锚索的参数振动模型

Fig. 1  Parametric vibration model of tether

静力状态下锚索的张力为T₀=T₀(s)，s为弧长坐标，静力作用下锚索的长度为L_E，L_E=L[1+8(f/L)²]，倾角为θ，弹性模量为E，横截面积为A，锚索无应力状态下的单位长度质量为m，动荷载作用下的动力构形由u表示，表示沿锚索轴向的法线方向到静力平衡位置的位移。

根据Hamilton原理得到锚索的振动方程^[6]：

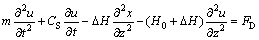  (2)

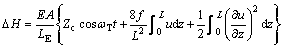 (3)

其中：ΔH为振动引起的附加锚索张力；C_s为锚索的黏性阻尼系数。由小垂度假设可知：T₀约等于沿z向的锚索初张力H₀，即T₀≈H₀，且ds≈dz；F_D为锚索振动引起的水体对锚索的作用力；锚索的跨中垂度为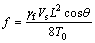(其中：γ_f为锚索的浮容重，V_s为锚索单位长度的体积)。

基于Morison公式，锚索横向振动引起的水体对锚索单位长度上的总作用力可表示为水体阻尼力和附加惯性力之和^[8]。

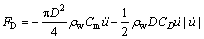      (4)

式中：C_m为附加质量系数，此处取C_m=1；D为锚索的外直径；ρ_w为海水的密度，此处取ρ_w=1 028 kg/m³；C_D为拖拽力系数，此处取C_D=0.7。

当悬浮隧道锚索的垂跨比很小时，可以近似取锚索的振动模态为标准弦的振动模态^[9]，即

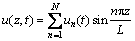             (5)

将式(5)代入式(2)，用伽辽金法^[10]化简式(2)，得：

；j=1，2，…，∞      (6)

式中：R(z，t)为留函数。

Tagata^[11]认为，对于张紧弦的端部激励振动，第一阶模态占主导地位，因此，本文取第一阶振动模态化简式(6)，得

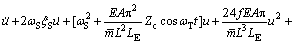
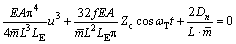    (7)

其中：；ω_S为锚索的第一阶固有频率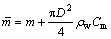；，为单位长度水体附加质量和锚索质量之和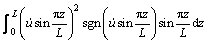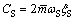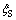； ；；为锚索的阻尼比。

2  锚索的稳定性分析

通常采用求解平稳状态的奇点特性和在原平衡微分方程上施加微小摄动来分析振动系统的稳定性，第一种方法为标准的确定性非线性系统稳定性分析方法，第二种方法结合Lyapunov指数特性，既可以求解确定性系统，又可以求解随机振动系统的稳定性问题^[12]。

本文采用Lyapunov指数法对锚索的参数振动进行稳定性分析，对一个微小的摄动，若摄动运动与无摄动运动非常接近，则运动是稳定的；否则，若运动不稳定，则微小的摄动会引起运动极其明显的变化。

Lyaponov指数I是相空间相邻轨迹发散或收敛的平均指数测度，它们表示任意动态过程的稳定性质。最大的Lyaponov指数I决定了过程的稳定性，当I＜0时稳定，否则不稳定^[13]。

3  数值分析与结果

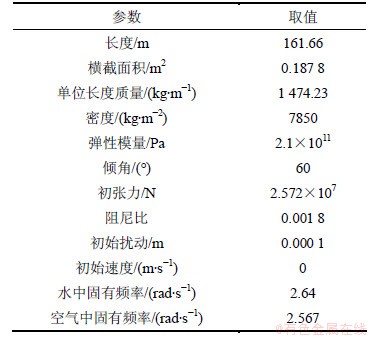
目前第一座悬浮隧道尚未面世，本研究锚索基本参数的选取参考了国外拟建悬浮隧道^[14]的设计参数，具体取值如表1所示。

表1  基本参数

Table 1  Basic parameters

采用MATLAB编制程序进行Lyapunov指数的求解，其求解迭代图形如图2所示，为消除瞬态振动的影响，前50 s的数据未予考虑。

图2  Lyapunov指数求解图

Fig. 2  Lyapunov exponent solving graph

3.1  索端参数激励幅值Z_c对其稳定性的影响

为了考虑空气中锚索和水中锚索振动稳定性的不同，分别考虑了2种情况下锚索随着Z_c变化的振动稳定性。分析时取锚索端部激励频率与锚索固有频率的比值为2。索端参数激励幅值和锚索稳定性的关系如图3所示。从图3可见：随着索端激励幅值的增大，锚索的振动逐渐从稳定状态变为不稳定状态；当索端激励为0.004 m时，处于空气中的锚索从稳定状态转变为不稳定状态；当索端激励为0.037 m时，处于水中的锚索从稳定状态转变为不稳定状态。对比2种情况下锚索振动的稳定状态可知：由于水体阻尼力的作用，水中锚索达到不稳定状态比空气中锚索需要的索端激励大。

图3  索端参数激励幅值和锚索稳定性的关系

Fig. 3  Relationship between parametric excitation amplitude of tether end and stability of tether

3.2  阻尼对锚索振动稳定性的影响

取索端激励频率为锚索固有频率的2倍，索端激励幅值为0.02 m，阻尼对锚索振动稳定性的影响如图4所示。从图4可见：随着锚索阻尼比的增大，锚索逐渐从不稳定的状态转变为稳定状态。因此，加大锚索的阻尼可使锚索更易处于稳定状态。

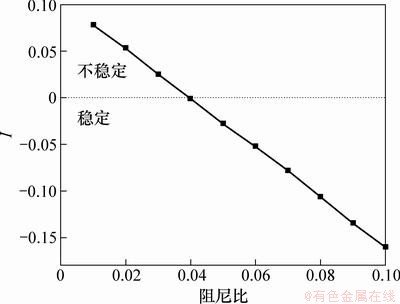
图4  阻尼比和锚索稳定性的关系

Fig. 4  Relationship between damping ratio and stability of tehter

3.3  索端激励频率对锚索振动稳定性的影响

取索端激励幅值范围为0.03~0.06 m，索端激励频率范围为1.8ω_S~2.2ω_S，索端激励频率对锚索振动稳定性的影响如图5所示。从图5可见：当索端激励幅值为0.03 m时，所有Lyapunov指数I均小于0，这表明系统总是稳定的，而与激励频率无关。幅值增至0.06 m时，索端激励频率在1.8ω_S~2.16ω_S范围内，I均大于0。由此可见：锚索参数振动失稳的范围不仅取决于索端激励幅值，而且取决于索端激励频率和锚索固有频率的关系。当索端激励频率为锚索固有频率2倍左右时，锚索最易发生失稳。

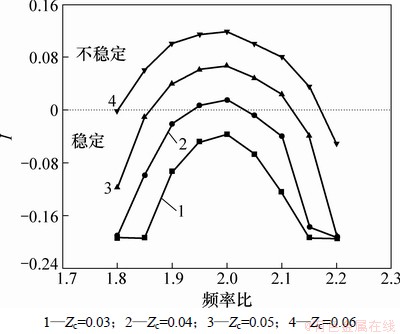
图5  不同激励幅值和频率的Lyaponov指数

Fig. 5  Corresponding Lyaponov exponent of different excitation amplitudes and frequencies

索端激励幅值和频率不同时锚索的稳定与不稳定区域如图6所示。由图6可以看出：随着索端激励幅值的增加，锚索参数振动不稳定区域逐渐增大；锚索参数振动失稳区域范围不大。

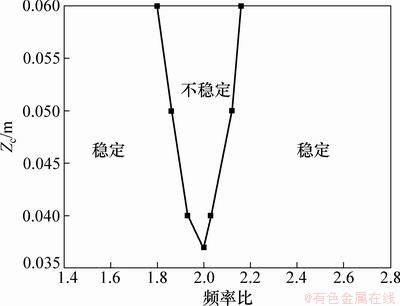
图6  不同激励幅值和频率作用下的稳定区和不稳定区

Fig. 6  Stable region and unstable region of different excitation amplitude and frequency

4  结论

(1) 由于水体阻尼力的作用，锚索处于水中比在空气中更易趋于稳定状态。

(2) 锚索振动系统阻尼比越大，锚索越易趋于稳定状态。

(3) 锚索参数振动失稳的范围取决于索端激励幅值和锚索端部激励频率与锚索固有频率的关系；当索端激励频率为锚索固有频率2倍左右时，锚索最易发生失稳。

(4) 随着索端激励幅值的增大，锚索参数振动不稳定区域逐渐增大，锚索参数振动不稳定区域范围不大。

参考文献：

[1] 陈健云, 孙胜男, 苏志彬. 水流作用下悬浮隧道锚索的动力响应[J]. 工程力学, 2008, 25(10): 229-234.

Chen Jianyun, Sun Shengnan, Su Zhibin. Dynamic response of submerged floating tunnel tethers subjected to current[J]. Engineering Mechanics, 25(10): 229-234.

[2] 孙胜男, 陈健云, 苏志彬. 悬浮隧道锚索-隧道耦合非线性参数振动研究[J].振动与冲击, 2007, 26(10): 104-108.

Sun Shengnan, Chen Jianyun, Su Zhibin. Study on nonlinear parametric vibration of a tether-tube coupled and submerged floating tunnel [J]. Journal of Vibration and Shock, 2007, 26(10): 104-108.

[3] Haugerud S A, Olsen T O, Muttoni A. The lake lugano crossing- technical solutions[C]//Strait Crossing 2001. Bergen, Norway: Swets & Zeitlinger Publishers Lisse, 2001: 563-568.

[4] 葛斐, 董满生, 惠磊, 等. 水中悬浮隧道锚索在波流场中的涡激动力响应[J]. 工程力学, 2006, 23(S1): 217-221.

Ge Fei, Dong Mansheng, Hui lei, et al. Vortex-induced vibration of submerged floating tunnel tethers under wave and current effects [J]. Engineering Mechanics, 2006, 23(S1): 217-221.

[5] Di Pilato M, Perotti F, Fogazzi P. 3D dynamic response of submerged floating tunnels under seismic and hydrodynamic excitation [J]. Engineering Structures, 2008, 30(1): 268-281.

[6] Sun Shengnan, Chen Jianyun, Li Jing. Non-linear response of tethers subjected to parametric excitation in submerged floating tunnels[J]. China Ocean Engineering, 2009, 23(1): 167-174.

[7] Sun Bingnan, Wang Zhigang, Kao J M, et al. Cable oscillation induced by parametric excitation of cable-stayed bridge[J]. Advances in Structural Dynamics, 2000, 1: 553-560.

[8] Sun Shengnan, Su Zhibin, Parametric vibration of submerged floating tunnel tether under random excitation[J]. China Ocean Engineering, 2011, 25(2): 349-356.

[9] Irvine H M. Cable structures[M]. Cambridge: Massachusetts Institute of Technology Press, 1981: 124-158.

[10] 麦继婷, 罗忠贤, 关宝树. 流作用下悬浮隧道张力腿的涡激动力响应[J]. 西南交通大学学报, 2004, 39(5): 600-604.

MAI Jiting, LUO Zhongxian, GUAN Baoshu. Vortex-induced dynamic response of tension legs for submerged floating tunnel under current effect[J]. Journal of Southwest Jiaotong University, 2004, 39(5): 600-604.

[11] Tagata G. Harmonically forced, finite amplitude vibration of a string[J]. Journal of Sound and Vibration, 1977, 51(4): 438-492.

[12] XIA Yong, Fujino Y. Auto-parametric vibration of a cable stayed-beam structure under random excitation[J]. Journal of Engineering Mechanics, 2006, 5: 279-286.

[13] 宋军伟, 方坤河. 应用Lyapunov指数研究混凝土阶段特征的稳定判据[J]. 重庆建筑大学学报, 2008, 30(3): 129-133.

SONG Junwei, FANG Kunhe. Research on stability criterion of concrete feature in different stress stage with Lyapunov exponent[J]. Journal of Chongqing Jianzhu University, 2008, 30(3): 129-133.

[14] 孙胜男, 陈健云, 苏志彬. 悬浮隧道锚索粘弹性阻尼器最优阻尼系数研究[J]. 中南大学学报: 自然科学版, 2011, 42(6): 1791-1796.

SUN Shengnan, CHEN Jianyun, SU Zhibin. Optimal damping coefficient of viscoelastic damper for submerged floating tunnel tether[J]. Journal of Central South University: Science and Technology, 2011, 42(6): 1791-1796.

(编辑  何运斌)

收稿日期：2012-03-21；修回日期：2012-05-28

基金项目：国家自然科学基金资助项目(51108224)；山东省优秀中青年科学家科研奖励基金资助项目(BS2010HZ005)

通信作者：孙胜男(1982-)，女，山东莱阳人，博士，副教授，从事悬浮隧道动力响应研究；电话：0635-8239080；E-mail：sunshengnan1982@163.com