Adaptive direct feedback linearization control of all-electric tank gun system
WANG Hong-yan(王洪艳)1, QIAO Ji-hong(乔继红)2
(1. Department of Information Engineering, Academy of Armored Force Engineering,Beijing 100072, China;
2. College of Information Engineering, Beijing Technology and Business University, Beijing 100081, China)
Abstract: Considering the whole impact of mechanical and electrical system nonlinearities, the direct feedback linearization (DFL) control strategy was used in the AC all-electrical tank gun control system to achieve a completely dynamic decoupling model. On the basis of DEF, in order to reduce the effect of changes in the system parameters and load torque, an adaptive wavelet neural network compensator to compensate for DEF error is proposed, which can reduce DEF control law reliance on the tank gun system model, and further enhance the speed tracking performance, robustness and adaptive capacity of AC tank gun control system. Computer simulations show that the tracking accuracy is much better and the control system has strong adaptability and robustness.
Key words: ARROW-WTCP; transport protocol; stability; convergence; fairness; IEEE 802.11
CLC number: TP271 Document code: A Article ID: 1672-7207(2011)S1-0360-05
1 Introduction
Tank AC all-electric gun control system mainly refers to the horizontal and the vertical tank gun control system used to control motor servo amplifier to replace the original DC motors and electro-hydraulic control method. This all-electric control system has simple structure, high efficiency, easy maintenance, etc, thus is widely paid attention all around the world[1].
The tank gun control system can work in three states: targeting, stability, and servo, so its horizontal subsystem and vertical subsystem are composed of the power drive control system, gyros, actuators, mechanical transmission device and other components. The whole system is a typical PMSM control system essentially[2].
AC speed control technology has already matured now. PMSM vector control can be used to obtain more excellent performance. But in the vector control, transient phenomenon in the magnetic field is still nonlinear and coupled. Furthermore, vector control doesn’t consider electrical and mechanical nonlinear effects on the whole system. For high-precision control of speed tracking, in addition to considering the load and other disturbances, the impact of non-linear motor model is also a key factor, as the nonlinear coupling of speed and current will lead directly to the quality of tracking speed. In this work, direct feedback linearization (DFL) control strategy was proposed based on the AC tank gun control system integrated non-linear mathematical model. Through the output variable Lie deriving, permanent magnet synchronous motor system was input-output linearized, furthermore achieving a completely dynamic decoupling model. In order to reduce the effect of changes in the system parameters and load torque, an adaptive wavelet neural network compensator to compensate for DFL error was proposed. It can reduce DFL control law reliance on the tank gun system model, and further enhance the AC tank gun control system speed tracking performance, robustness and adaptive capacity.
2 Problem description
Consider the parameter uncertainty and exchange in all-electric gun permanent magnet synchronous motor control system to write a mathematical model[3]:
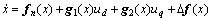 (1)
(1)
where
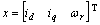
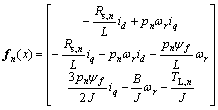
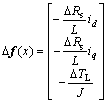
g1=[1/L, 0, 0]T, g2=[0, 1/L, 0]T, Rs,n and TL,n are nominal values. Define uncertainty as
?Rs=Rs-Rs,n, ?TL=TL-TL,n
3 Direct feedback linearization control of AC all-electrical tank gun control system
In order to realize the decoupling of the system, and avoid the zero dynamics problem[4], select ωr and id as the system outputs and define a new output variable:
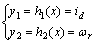 (2)
(2)
Differentiating Eq.(2) [5], it yields
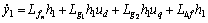 (3)
(3)
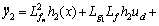
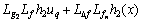 (4)
(4)
where

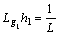
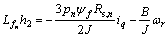
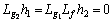
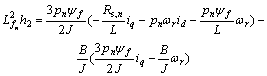
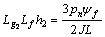
Introducing control variable: 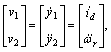
the following equations can be obtained by linear control theory:
 (5)
(5)
The actual control variables can be obtained by the direct feedback linearization as
 (6)
(6)
where
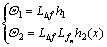 (7)
(7)
If Θ1 and Θ2 can be accurately got, substitution of Eq.(6) into Eq.(3) and Eq.(4) respectively yields
 (8)
(8)
So, the system control problem is changed into finding the id and ω, and making them follow any given expected value id,ref and ωref, respectively. By selecting k1, k2 and k3, the system has a negative characteristic root. We can make the tracking error approach zero with time. However, due to parameter variations, load disturbances and other uncertainties, the uncertainties of the direct feedback linearization Θ1, Θ2 are not exactly known. Therefore, relying on the direct feedback linearization control, the nonlinear tank gun control system cannot be completely converted to a linear system, thus causing the error; even worse, the controller may result in invalidation. Because WNN can approximate any nonlinear function, a WNN is designed to mimic the uncertainties Θ1, Θ2 in this work.
4 Adaptive WNN-based direct feedback linearization control system design
A two-layer product WNN[6] is shown in Fig.1, which is comprised of a product layer and an output layer. A family of wavelets is constructed by translations and dilations performed on a single fixed function called the mother wavelet. The first derivative of a Gaussian function ψ(x)=-xexp(-x2/2) was adopted as a mother wavelet in this work.
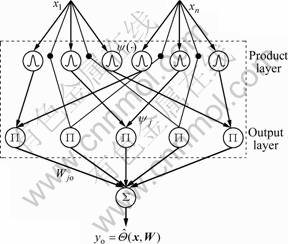
Fig.1 Two-layer product WNN structure
The output of WNN is
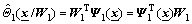 (9)
(9)
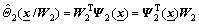 (10)
(10)
where Wi=[Wi1 Wi2 …Wiq]T∈Rq, Ψi=[Ψi1 Ψi2 … Ψiq]T∈Rq, i=1, 2.
If Θ1, Θ2 can be well approximated by WNN, the actual control variables are changed as
 (11)
(11)
Adopting linear control (5), the error vector equation can be obtained as
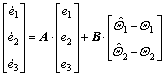 (12)
(12)
where
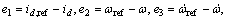
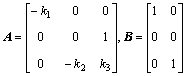
According to the approximation error analysis[7], there exists an ideal vector W* of a WNN such that
 (13)
(13)
 (14)
(14)
where 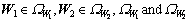 are such sets as
are such sets as
 and
and 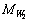 are parameters to be designed.
are parameters to be designed. 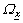 is the reachable area of system states.
is the reachable area of system states.
According to the infinite approximation of wavelet neural networks, the following equations are defined:
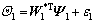 (15)
(15)
 (16)
(16)
Setting 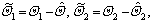 the following equations are obtained:
the following equations are obtained:
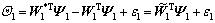 (17)
(17)
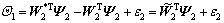 (18)
(18)
where 
WNN is used to compensate the uncertainties impact in the direct feedback linearization control on system. The design of WNN compensator should ensure that the unknown uncertainties can be observed, and the parameters of the neural network can be adjusted adaptively, thus can track accurately the changes of uncertainties in time. In practice, there is the reconstruction error of wavelet neural network, therefore, robust compensation is required. The system structure is shown in Fig.2.
Considering the robust compensator ua, defining 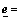 [e1 e2 e3] T and ua=[ua1 ua2] T, Eq.(12) is changed into
[e1 e2 e3] T and ua=[ua1 ua2] T, Eq.(12) is changed into
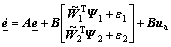 (19)
(19)
The goal of system control is to design robust adaptive controller, which can ensure the stability of both the disturbance observation error and the tracking error, and then may make the output and its every order derivation follow reference signal and its relevant derivation, and the tracking error of system has H∞ capability.
By the analysis, a theory is obtained as follows.
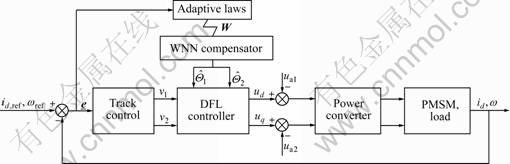
Fig.2 Structure of direct feedback linearization-based WNN
Theorem: Consider the servo system represented by Eq.(1). If the control law is designed as Eq.(11), WNN is used to compensate the uncertainties. The adaptive learning algorithms of WNN are designed as Eq.(20) and the robust compensator is designed as Eq.(21), then the stability of the proposed adaptive control system based on DFL can be guaranteed. The tracking error is lower than given performance index as Eq.(22).
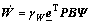 (20)
(20)
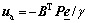 (21)
(21)
 ≤
≤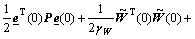
 (22)
(22)
where W=[W1 W2] T, Ψ=[Ψ1 Ψ2] T, γW is the positive learning rate and 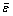 is the approximate error upper boundary of WNN. Q is the positive matrix and P=P T>0 is the solution of the following equation:
is the approximate error upper boundary of WNN. Q is the positive matrix and P=P T>0 is the solution of the following equation:
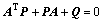 (23)
(23)
Proof: Let the Lyapunov function candidate be given by
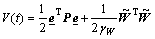 (24)
(24)
Differentiating Eq.(24) with respect to time and using Eq.(19), there is
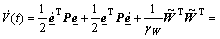
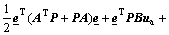
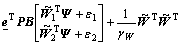 (25)
(25)
Consider Eqs.(20) and (21):
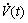 ≤
≤ ≤
≤
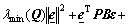
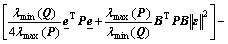
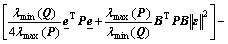
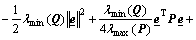
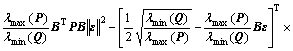
 (26)
(26)
When 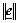 >
>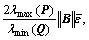 the following formula can be obtained:
the following formula can be obtained:
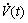 ≤
≤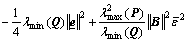 <0 (27)
<0 (27)
Since 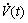 <0 is a negative function, the asymptotical stability of system can be guaranteed.
<0 is a negative function, the asymptotical stability of system can be guaranteed.
Calculate Eq.(27) integral from t=0 to t=T:
V(T)-V(0)≤
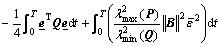 (28)
(28)
From Eq.(24), V(T)≥0, combining Eqs.(24) and (28) yields
 ≤
≤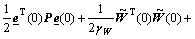
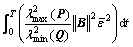 (29)
(29)
In the view of Eq.(29), using the adaptive learning algorithms (20) and the robust compensator (21), the parameter error e is uniformly ultimately bounded, and the tracking error is lower than the given performance index and the proof is completed.
5 Simulation research
In order to verify the effectiveness of direct feedback linearization control based on WNN, AC all-electric gun control horizontal sub-system is used in simulation research. Coefficients k1=30, k2=350, k3=30, id,ref are the given signals. The input of WNN is x=[id, iq, ω]T, outputs are 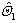 and
and 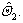 Select 11 hidden layers,
Select 11 hidden layers,
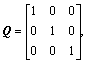
work out the Riccati equation (23), get

and design parameter γW=2.0.
1) Performance of system with load disturbance
Consider AC all-electric gun control system with the load disturbance (converted to motor shaft) TL= 3.38sin(t-3). Comparison of the use of WNN compensation and no compensation for the direct feedback linearization control is conducted, and the tracking simulation results are shown in Fig.3.
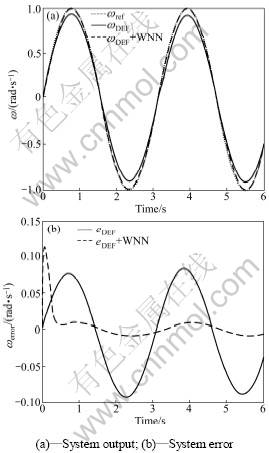
Fig.3 Comparison of tracking simulation results with TL=3.38sin(t-3)
2) Performance of system parameter variation
The system parameters Rs=Rs,n[1+0.2sin(2t)], where Rs,n is the nominal value. Still use the above control method to test the controller robustness of the system uncertainty, and the simulation results are shown in Fig.4.
Simulation results show that the system tracking performance is deteriorated using only direct feedback linearization control when the system load changes or parameters are uncertain. With compensation for the use of wavelet neural network, the system tracking performance obviously performs better. This shows that the wavelet neural network online can reach the expected goal.
6 Conclusions
Direct feedback linearization method is fit for nonlinear and strong coupling system. It is used to linearize AC all-electrical tank gun control system, and a completely dynamic decoupling model is obtained. In order to reduce the effect of changes in the system parameters and load torque on the basis of DFL, an adaptive wavelet neural network compensator for DEF error is proposed, which can reduce DFL control law reliance on the tank gun system model, and can further enhance the AC tank gun control system speed tracking performance, robustness and adaptive capacity.
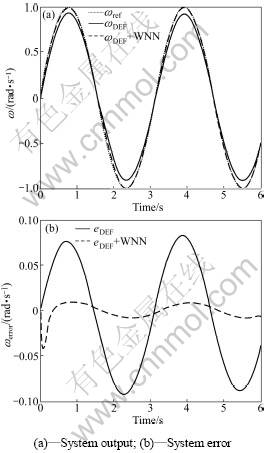
Fig.4 Simulation results of controller robustness
References
[1] ZHANG Cheng-liang. Tank gun control system[M]. Beijing: Academy of Armored Force Engineering, 1998.
[2] ZANG Ke-mao, LI Li-yu, LI Kuang-cheng. A study on A.C. all-electric gun control system in tanks[J]. Acta Armamentarii, 2006, 27(3): 549-552.
[3] WANG Hong-yan. Robust control method research of AC All-electrical tank gun control system[D]. Beijing: Beijing Institute of Technology, 2008.
[4] LIU Dong-liang. Research on PMSM servo system and nonlinear control strategy[D]. Hangzhou: Zhejiang University, 2005.
[5] HE Yu-yao, YAN Mao-de. Non-linear control theory and applications [M]. Xi’an: University of Electronic Science and Technology Press, 2007.
[6] Wai R J, Duan R Y, Lee J D. Wavelet neural network control for induction motor drive using sliding-mode design technique[J]. IEEE Transactions on Industry Electronics, 2003, 50(4): 733-748
[7] Delyon B, Juditsky A, Benveniste A. Accuracy analysis for wavelet approximations[J]. IEEE Transactions on Neural Networks, 1995, 6(2): 332-348.
(Edited by YANG Bing)
Received date: 2011-04-15; Accepted date: 2011-06-15
Corresponding author: WANG Hong-yan; Tel: +86-15010504816; E-mail: zxywhy2000@sina.com