J. Cent. South Univ. Technol. (2011) 18: 823-829

DOI: 10.1007/s11771-011-0768-5

A new clustering algorithm for large datasets

LI Qing-feng(李清峰)^{1, 2}, PENG Wen-feng(彭文峰)¹

1. Department of Computer and Electronic Engineering, Hunan University of Commerce, Changsha 410205, China;

2. School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: The Circle algorithm was proposed for large datasets. The idea of the algorithm is to find a set of vertices that are close to each other and far from other vertices. This algorithm makes use of the connection between clustering aggregation and the problem of correlation clustering. The best deterministic approximation algorithm was provided for the variation of the correlation of clustering problem, and showed how sampling can be used to scale the algorithms for large datasets. An extensive empirical evaluation was given for the usefulness of the problem and the solutions. The results show that this method achieves more than 50% reduction in the running time without sacrificing the quality of the clustering.

Key words: data mining; Circle algorithm; clustering categorical data; clustering aggregation

1 Introduction

Clustering aims at providing useful information by organizing data into groups (referred to as clusters). It is applicable in many real-life applications because there is typically a large amount of unlaboured data. Such data may contain information not previously known or changed rapidly (e.g., genes of unknown function, dynamically changing webpages in an automatic web, and document classification system). On the other hand, labeled data are often limited, as well as difficult and expensive to generate because the labeling procedure requires human expertise.

The problem of clustering aggregation was previously considered in the machine learning community. AILON et al [1] applied the clustering aggregation idea to a collection of soft clusterings obtained by random projections. They used an agglomerative algorithm, but they were penalized for merging dissimilar nodes. ANDRITSOS et al [2] proposed to use a single linkage algorithm to combine multiple runs of the k-means algorithm. BANSAL et al [3] observed the connection between clustering aggregation and clustering of categorical data. They proposed information theoretic distance measures, and genetic algorithms for finding the best aggregation solution. BARTHELEMY et al [4] used linear programming to discover a correspondence between the labels of the individual clusterings and those of an optimal meter clustering. BOULIS et al [5] defined clustering aggregation as a maximum likelihood estimation problem, and they proposed an EM algorithm for finding the consensus clustering. CHARIKAR et al [6] considered the distance measure between clusterings. They proposed a simulating annealing algorithm for finding an aggregate solution and a local search algorithm and applied clustering aggregation to the analysis of microarray data. CRISTOFOR and SIMOVICI [7] considered the problem of aggregation for segmentations of sequential data. Segmentation can be thought as an order-preserving clustering. They showed that the problem can be solved optimally using dynamic programming.

In this work, an approach to clustering is considered based on the concept of aggregation, by assuming that a set of data objects are given, and then some information on these objects should be clustered. This information comes in the form of m clusterings, C₁, …, C_m. The objective is to produce a single clustering C that agrees as much as possible with m input clusterings. A disagreement is defined between two clusterings C′ and C″ as a pair of objects (v, u) such that C′ places them in the same cluster, while C″ places them in different clusters or vice versa. If d(C′, C″) denotes the number of disagreement between C′ and C″, the task is to find a clustering C that minimizes

2 Description of relational work

Considering a set of n objects V={v₁, …, v_n}, a clustering C of V is a partition of V into k disjoint sets C₁, …, C_k, that is, 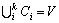and C_i∩C_j = for all i≠j. The k sets C₁,…,C_k are the clusters of C. For each v∈V, C(v) is used to denote the label of the cluster to which the object v belongs, that is, C(v)=j if and only if v∈C_j. In this work, m clusterings are considered: C_i denotes the i-th clustering, and k_i is the number of clusters of C_i.

In clustering aggregation problem, the task is to find a clustering that minimizes disagreements with a set of input clusterings. To make the notion more precise, a measure of disagreement between clusterings needs to be defined. Considering two objects u and v in V, the following simple 0/1 indicator function is used to check if two clusterings C₁ and C₂ disagree on the clustering of u and v:

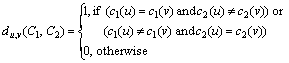(1)

The distance between two clusterings C₁ and C₂ is defined as the number of pairs of objects on which the two clusterings disagree, that is,

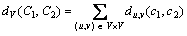                              (2)

Problem 1 For a set of objects V and m clusterings C₁, …, C_m in V, a new clustering C is calculated to minimize the total of disagreements:

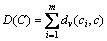                                                      (3)

Theorem 1 For a set of objects V, and clusterings C₁, C₂, C₃ in V, there is d_V(C₁, C₃)≤d_V(C₁, C₂)+d_V(C₂, C₃).

Proof Since d_u,v takes 0/1 values, the only case in which the triangle inequality could be violated is  d_u,v(C₁, C₃)=1 and d_u,v(C₁, C₂)=d_u,v(C₂, C₃)= 0. However, d_u,v(C₁, C₃)=1 implies either C₁(u)=C₁(v) and C₃(u)≠ C₃(v) or C₁(u)≠C₁(v) and C₃(u)=C₃(v). Assume that C₁(u)=C₁(v) and C₃(u)≠C₃(v). Then, d_u,v(C₁, C₂)=0 implies the clusterings C₁ and C₂ agree on the clustering of u and v; therefore, C₂(u)=C₂(v). However, since d_u,v(C₂, C₃)=0, C₂ and C₃ are also in agreement, thus C₃(u)=C₃(v), which contradicts this assumption that C₃(u)≠C₃(v). The case of C₁(u)≠C₁(v) and C₃(u)= C₃(v) is treated symmetrically.

Problem 2 Given a set of objects V, and distances X_uv∈[0, 1] for all pairs (u, v)∈V, find a partition C for the objects in V that minimizes

Given the m clusterings C₁, …, C_m asinput, one can construct an instance of the correlation clustering problem by defining the distances X_uv appropriately.

Defining that X_uv =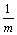|{i:1≤i≤m and c_i(u)≠c_i(v)}| is the

fraction of clusterings that assign the pair (u, v) into different clusters.

Theorem 2 For all u, v and w in V, there is X_uw≤ X_uv+X_vw.

Proof  Define the indicator function  such that  if C_i(u)≠C_i(v) and zero otherwise, then X_uv=

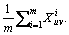 Therefore, it suffices to show that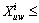

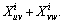 The only way that this inequality can be violated is  and 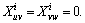 However, the latter equality suggests that u, v, w are all placed in the same cluster, thus reaching a contradiction.

3 Description of algorithm

The Circle algorithm can work in the correlation clustering problem. The input data are viewed as a graph whose vertices are the tuples of a dataset, and the edges are weighted by the distances X_uv. The algorithm is defined with an input parameter α, and it is the only algorithm that requires an input parameter. The aim is to find a set of vertices that are close to each other and far from other vertices. Such a set is considered to be a cluster, and should be removed from the graph; then the rest of the vertices are proceeded. The difficulty lies in finding such a set since in principle any subset of the vertices can be a candidate. The difficulty is overcome by resorting again to the triangle inequality. In order to find a good cluster, all vertices that are close (within a circle) to a vertex u are taken. The triangle inequality guarantees that if two vertices are close to u, then they are also relatively close to each other.

It first sorts the vertices in increasing order of the total weight of the edges incident on each vertex. At every step, the algorithm picks the first unclustered node u in that ordering. It then finds the set of nodes B that are at a distance of at most 1/2 from the node u, and computes the average distance d(u, B) of the nodes in B to node u. If d(u, B)≤α, then the nodes in B∪{u} are considered to form a cluster; otherwise, node u forms a singleton cluster. It can be proved that, when setting α=1/4, the cost of a solution produced by the Circle algorithm is guaranteed to be at most three times that of the optimal clustering.

4 Theoretical analysis

The Circle algorithm is an approximation algorithm for the correlation clustering problem (Problem 2). The input I to the problem is a set of n points and the pairwise distances X_uv. The cost function is d(C) defined in Eq.(3). The approximation ratio of the algorithm is bounded by a constant. First, the following general lemma is proved.

Lemma 1 For any algorithm ALG and any pair of objects (u, v), if 1) X_uv≤c and ALG assigns u and v in the same cluster, or 2) X_uv≥1-c and ALG assigns u and v in different clusters, the cost on edge (u, v) is at most (c/1-c) times that of the optimal algorithm for (u, v).

Proof In both cases 1) and 2), the algorithm ALG pays at most c. If it takes the opposite decision, then it pays at least 1-c, hence the ratio is c/(1-c). As an obvious corollary, if X_uv≤1/2 and an algorithm assigns u and v to the same cluster, or if X_uv≥1/2 and an algorithm assigns u and v to different clusters, then the algorithm cannot do worse than the optimal on (u, v).

Theorem 3 The Circle algorithm has approximation

ratio max{  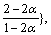 for α=1/4, the

algorithm achieves an approximation ratio of 3.

Proof The algorithm is analyzed by bounding the cost that the algorithm pays for each edge in terms of the cost that the optimal algorithm pays for the same edge. Consider an iteration of the Circle algorithm, and let u be the node selected to be the center of the ball.

1) Singleton clusters

First, consider the case that C = {u} is selected to be a singleton cluster. Recall that B is the set of nodes that are within distance 1/2 from u and in this case the average distance d(u, B) of the nodes is more than α. For all edges (u, i) with 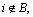 there is X_ui≥1/2. Since the algorithm separates u from i, the cost of the optimal cannot be less on each (u, i). The algorithm splits all edges (u, i) with  so the cost is

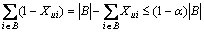
where  from the fact that the algorithm

chooses {u} to be a singleton cluster.

On the other hand, the optimal algorithm might choose to place u in the same cluster with some vertices  Thus, the cost of the optimal for the edges from u to the set B is

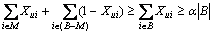
where iB, X_ui≤1/2, and thus 1-X_ui≥X_ui. So, the approximation ratio achieved on dges incident to the singleton clusters is at most

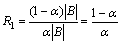
2) Edges within clusters

For the edges of type (u, i) with i∈B that the algorithm places in the cluster C, there is X_ui≤1/2, so the optimal algorithm cannot improve the cost by splitting those edges. The other types of edge within the cluster C=B∪{u} are edges (i, j) with i, j∈B. The vertices i∈B are arranged in order of increasing distance X_ui from the node u. For a fixed j, the cost of the edges (i, j) will be bounded for i < j.

If X_uj≤β for a constant β<1/2, by the triangle inequality, for all iij≤X_ui+X_uj≤2β. Therefore, by Lemma 1, the approximation ratio for those edges is at most

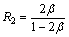
If X_uj>β, let C_j be the set of vertices i with ij is also less than α since C_j contains a prefix from the list of vertices ordered in ascending order of their distance X_ui from node u. The cost of the algorithm for the edges (i, j) where i is in C_j is

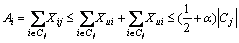              (4)

On the other hand, assume that the optimal algorithm places some vertices iM_jC_j in the same cluster, and the rest of the vertices iS_j=C_j-M_j in different clusters; thus |C_j|=|M_j|+|S_j|. The cost of the optimal algorithm for edges (i, j) where i is in C_j can be written as

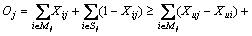
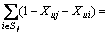
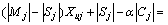
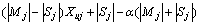                   (5)

If |M_j|<|S_j|, X_uj≤1/2 or (|M_j|-|S_j|)X_uj≥(|M_j|-|S_j|)/2, so the cost of the optimal is

O_j≥(|M_j|-|S_j|)/2+|S_j|-α(|M_j|+|S_j|)=

(1/2-α)(|M_j|+|S_j|)=(1/2-α)|C_j|

In this case, the approximation factor is

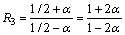
If |M_j|≥|S_j| and X_uj≥β, then the cost of the optimal algorithm is

O_j≥β(|M_j|-|S_j|)+|S_j|-α(|M_j|+|S_j|)=(β-α)|M_j|+(1-β-α)|S_j|

Selecting β≥α, there is O_j≥(1-2α)|S_j|.

=

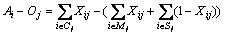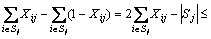
                                          (6)

where X_ij≤1 for all edges (i, j).

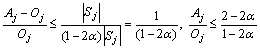
The approximation factor is at most

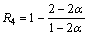
Note that R₂ is an increasing function of β. Since β≥α, it takes its minimum value for β=α. Here, R₂≤R₃, and R₂≤R₄ for all α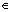(0, 1/2), so the approximation ratio for the edges within a cluster is at most max{R₃, R₄}.

3) Edges across clusters

The cost of edges is bounded to go from inside C to clusters outside C. For edges of the type (u, i) with iC, there is X_ui>1/2 and the algorithm splits those edges so that the optimal algorithm cannot perform better on any one of those edges. Therefore, edges of the type (i, j) with  and  are concentrated on. In particular, X_ui≤1/2 and X_uj>1/2. If X_uj ≥ γ for a constant γ>1/2 to be specified later, there is X_ij≥X_ui-X_uj≥γ-1/2. So, from Lemma 1, the approximation ratio on those edges will be at most

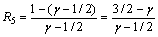
In the remaining case 1/2uj<γ, the algorithm is proceeded by fixing j and bounding the cost of all edges (i, j) for i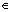C. For some fixed j, it is assumed that the optimal algorithm places some vertices  in the same cluster, and the rest of the vertices i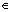S_j =C-M_j in different clusters. The cost of the algorithm for all edges (i, j) with i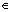C is

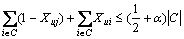                     (7)

The cost of the optimal algorithm is bounded as

O_j ≥(|M_j|-|S_j|)?X_uj+|S_j|-α(|M_j|+|S_j|)

If |M_j|≥|S_j|, then X_uj>1/2, so the cost of the optimal

algorithm is O_j≥ and the approximation ratio

is R₃.

If |M_j|<|S_j|, then X_uj<γ, therefore

O_j≥γ(|M_j|-|S_j|)+|S_j|-α(|M_j|+|S_j|)=(γ-α)|M_j|+(1-γ-α)|S_j|

Selecting γ≤1-α, it yields O_j≥(1-2α)|M_j|.

Considering the difference A_j-O_j, there is

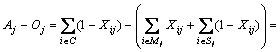
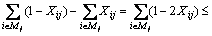
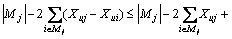
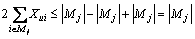                    (8)

where X_ui≤1/2 and X_uj>1/2. Similarly, 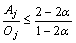 is

obtained. Therefore, the approximation ratio in this case is again at most R₄.

It is noted that the ratio R₅ is a decreasing function of γ. Since γ≤1-α is selected, R₅ takes its minimum value

for γ=1-α, which is R₅== R₃.

The overall approximation ratio of the circle algorithm is R≤max{R₁, R₃, R₄}. The ratios R₁, R₃, and R₄ are functions of the parameter α. Here 0≤α≤1/2 [8], and R₁ is a decreasing function of α, while R₃ and R₄ are increasing functions of α. For α=1/4, the values of all three ratios is 3. Therefore, it is concluded that the approximation ratio of the Circle algorithm is at most 3.

5 Experimental evaluation

5.1 Robustness evaluation

The goal in this set of experiments was to show how the Circle algorithm could be used to improve the quality and robustness of widely-used vanilla clustering algorithms. The dataset is shown in Fig.1. An intuitively good clustering for this dataset consisted of seven perceptually distinct groups of points. Here, five different clustering algorithms were implemented in MATLAB: Ward’s clustering, complete linkage, single linkage, average linkage, and k-means algorithm. The first three algorithms are agglomerative bottom-up algorithms that merge pairs of clusters, based on their minimum, maximum, and average distance, respectively. Average linkage clustering algorithm is also an agglomerative bottom-up algorithm whose merging criterion is to select the pair of clusters that minimize the sum of the square of distances from each point to the mean of the two clusters. The k-means algorithm is the popular iterative clustering method which is also known as Lloyd’s algorithm. For all of the clusterings, the number of clusters is set to be 7, and for the other parameters, if any, MATLAB’s defaults are used. The results for the five clusterings are shown in Figs.1(a)-(e). One can see that all clusterings are imperfect. In fact, the dataset contains features that are known to create difficulties for the selected algorithms, such as narrow bridges between clusters, and uneven-sized clusters. The last panel in Fig.1(f) shows the results of aggregating five previous clusterings. The Circle algorithm is better than any of the input clusterings.

Fig.1 Clustering aggregation on different input clusterings: (a) Ward’s clustering; (b) Complete linkage; (c) Single linkage;       (d) Average linkage; (e) k-means algorithm; (f) Circle algorithm

5.2 Clustering categorical data

The goal in this experiment was to show how Circle algorithm could be used to identify the correct clusters as well as outliers. Three datasets were created as follows: k cluster centers were selected uniformly at random in the unit square, and 100 points were generated from the normal distribution around each cluster center. For three datasets, k=3, 5, 7 were used. An additional 20% of the total number of points were generated uniformly from the unit square and they were added in the datasets. For each of the three datasets, the k-means algorithm was run with k=2, 3, …, 10, and the resulting clusterings were aggregated. Actually, in each dataset, clustering aggregation was performed on nine input clusterings. Obviously, when k is too small, some clusters are merged, and when k is too large, some clusters are split. The results of Circle algorithm for the three datasets are shown in Fig.2. It can be seen that the main clusters identified are precisely the correct clusters. Some small additional clusters that contain only points from the background noise are also found, and they could be clearly characterized as outliers.

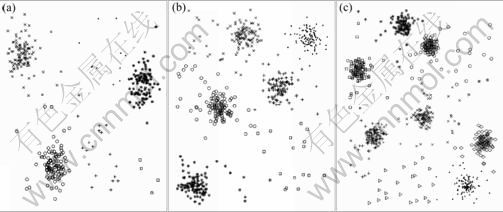
Fig.2 Results of finding correct clusters and outliers of Circle algorithm: (a) k=3; (b) k=5; (c) k=7

5.3 Precision  evaluation

In this experiment, Mushrooms dataset was used which contained information on physical characteristics of Mushrooms. There was 8 124 instances of Mushrooms, with each described by 22 categorical attributes such as shape, color, and odor. There was a class label describing if a mushroom was poisonous or edible, and there were  2 480 missing values in total. Comparative experiments were run with the categorical clustering algorithm ROCK [9] and LIMBO [10]. ROCK used the Jaccard coefficient to measure tuple similarity, and placed a link between two tuples whose similarity exceeded a threshold θ. For this experiment, values of θ that suggested by FERN [11] were used. LIMBO used information theoretic concepts to define clustering quality. It clustered tuples together so that the conditional entropy of the attribute values within a cluster was low. For the parameter Ф of LIMBO, values suggested by FAGIN [12] were used. For both algorithms, the convention of LIMBO algorithm was adopted, and missing values were treated as separate attribute values.

For each of the datasets, the clustering was evaluated using the class labels of the datasets. If a clustering contained k clusters with sizes s₁, …, s_k and the sizes of the majority class in each cluster were m₁, …, m_k, the quality of the clustering was measured by an impurity index measure (I) [13], defined as

                          (9)

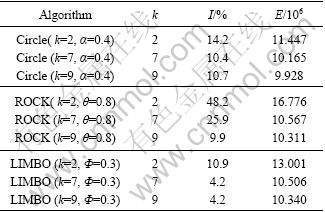
The results for the Mushrooms datasets are shown in Table 1. In addition to impurity index, the number of clusters of each clustering (k) and the disagreement error (E) [14-15] are shown. Since the clustering aggregation algorithms make their own decisions for the resulting number of clusters, the other two algorithms for the same values of k are run so that the fairness is ensured. Overall, the impurity indices are comparable with the exception of LIMBO’s impressive performance on Mushrooms for k=7 and k=9. This algorithm achieves low distance error. The distance error is close to theoretical lower bound that is computed by considering an idealized algorithm that merges all edges with weight less than 1/2, and splits all edges with weight more than 1/2.

Table 1 Results of mushrooms dataset

5.4 Handling large datasets

Experiments with the sampling algorithm allow us to apply clustering aggregation to large datasets. The Mushrooms dataset was used with the behavior of this algorithm as a function of the sample size. The number of clusters found with the nonsampling algorithms is around 10%. When sampling is used, the number of clusters found in the sample remains close to 10%. For small sample size, clustering the sample is relatively fast compared with the postprocessing phase of assigning the nonsampled points to the best cluster, and the overall running time of the sampling algorithm is linear. In Fig.3(a), the running time of the sampling algorithm is plotted as a function of the sample size. For a sample size of 1 800, more than 50% reduction is achieved in the running time. At the same time, the impurity index of the algorithm converges very fast to the value achieved by the nonsampling algorithms. For sample size of 1 800, the same impurity index with only half of the running time is obtained, as shown in Fig.3(b).

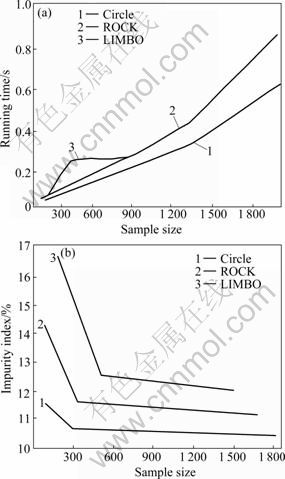
Fig.3 Scalabilities for sampling algorithm: (a) Running time as function of sample size; (b) Impurity index as function of sample size

6 Conclusions

1) A sampling mechanism is proposed that allows this algorithm to handle large datasets. The problem is considered as NP-hard, yet approximation for this algorithm is provided. For the formulation of correlation clustering, a combinatorial deterministic three- approximation algorithm is given, which is an improvement over the previously best known deterministic nine-approximation algorithm.

2) An extensive experimental study is presented and the benefits of this approach are demonstrated. Furthermore, it is shown that this sampling technique reduces half of running time without sacrificing the quality of the clustering.

References

[1] AILON N, CHARIKAR M, NEWMAN A. Aggregating inconsistent information: Ranking and clustering [C]// Proceedings of the ACM Symposium on Theory of Computing. Arlington: IEEE, 2009: 684- 693.

[2] ANDRITSOS P, TSAPARAS P, MILLER R J, SEVCIK K C, LIMBO. Scalable clustering of categorical data [C]// Proceedings of the International Conference on Extending Database Technology. Vancourer: IEEE, 2007: 123-146.

[3] BANSAL N, BLUM A, CHAWLA S. Correlation clustering in Machine Learn [M]. Cambridge: Kluwer Academic Publisher, 2008: 3-11.

[4] BARTHELEMY J, LECLERC B. The median procedure for partitions [J]. DIMACS Series in Discrete Mathematics, 2008, 41(10): 23-32.

[5] BOULIS C, OSTENDORF M. Combining multiple clustering systems [C]// Proceedings of the European Conference on Principles and Practice of Knowledge Discovery in Databases. Selangor: IEEE, 2005: 63-74.

[6] CHARIKAR M, GURUSWAMI V, WIRTH A. Clustering with qualitative information [C]// Proceedings of the IEEE Symposium on Foundations of Computer Science. Seattle: IEEE Computer Society, 2008: 524-533.

[7] CRISTOFOR D, SIMOVICI D A. An information-theoretical approach to genetic algorithms for clustering [J]. IEEE Communication Magazine, 2009, 23(6): 876-881.

[8] HAN J W, KAMBER M, FAN M, MENG X F. Data mining concepts and techniques [M]. Beijing: China Machine Press, 2001: 232-236.

[9] DEMAINE E D, EMANUEL D, FIAT A, IMMORLICA N. Correlation clustering in general weighted graphs [J]. Theoretical Computer Science, 2006, 36(1): 172-187.

[10] DWORK C, KUMAR R, NAOR M, SIVAKUMAR D. Rank aggregation methods for the Web [C]// Proceedings of the International World Wide Web Conference. Athens: IEEE, 2003: 613–622.

[11] FAGIN R, KUMAR R, SIVAKUMAR D. Comparing top kind lists [C]// Proceedings of the ACMSIAM Symposium on Discrete Algorithms. Alaska: IEEE,2008: 28–36.

[12] FERN X Z, BRODLEY C E. Random projection for high dimensional data clustering: A cluster ensemble approach [C]// Proceedings of the International Conference on Machine Learning. Texas: IEEE, 2003: 186–193.

[13] GUAN Qing-yang, ZHAO Hong-lin, GUO Qing. Cancellation for frequency offset in OFDM system based on TF-LMS algorithm [J]. Journal of Central South University of Technology, 2010, 17(6): 1293-1299.

[14] BAI S. Concept clustering under insufficient knowledge [J]. Chinese Journal of Computers, 1995, 18(6): 409-416.

[15] GUO J S, ZHAO Y, SHI P F. An efficient dynamic conceptual clustering algorithm for data mining [J]. Journal of Software, 2001, 12(4): 582-591.

(Edited by YANG Bing)

Foundation item: Projects(60873265, 60903222) supported by the National Natural Science Foundation of China; Project(IRT0661) supported by the Program for Changjiang Scholars and Innovative Research Team in University of China

Received date: 2011-01-12; Accepted date: 2011-04-24

Corresponding author: LI Qing-feng, Associate Professor; Tel: +86-13549643089; E-mail: lqf4pwf3@163.com