DOI: 10.11817/j.issn.1672-7207.2018.06.012
基于扰动观测器的制冷机组非奇异terminal滑模控制
刘君健,吴爱国,董娜
(天津大学 电气与自动化工程学院,天津,300072)
摘要:针对压缩制冷机组的温度控制问题,在分析机组机理的基础上,基于现有实验平台,采用改进的分区集中参数法,结合机理建模与实验辨识,提出制冷机组合理简化后的模型,并通过仿真与实验曲线对比,验证模型的准确性;设计蒸发器子系统的扰动观测器,证明扰动估计误差的有界性,并将扰动及其导数的估计值引入滑模面设计中;提出一种非奇异terminal滑模面,将二阶滑模与terminal滑模相结合,设计控制率,最后与传统滑模法进行仿真对比。研究结果表明:提出的控制方法对扰动具有良好的动态性能,同时消除了抖振。
关键词:制冷机组;扰动观测器;非奇异terminal滑模控制
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2018)06-1393-10
Non-singular terminal sliding mode control based on disturbance observer in refrigeration system
LIU Junjian, WU Aiguo, DONG Na
(School of Electrical Engineering & Automation, Tianjin University, Tianjin 300072, China)
Abstract: Considering the temperature control issue in refrigeration system, and based on the analysis of the mechanism of compression refrigeration system, a reasonable simplified model was proposed by improving zone lumped parameter method. Besides, mechanism modeling and experimental identification based on the experimental platform were combined together. The model was proved to be accurate through the simulation and experiment. A disturbance observer of evaporator was proposed, and then its error was proved to be bounded. The estimated value of disturbance and its derivative were used to design the sliding mode surface; the second-order sliding mode was combined with terminal sliding mode which was proved to be non-singular, and then the controlled variable was designed. The simulation results were compared with those of traditional method. The results show that the proposed method has better dynamic performance against disturbance and can eliminate chattering problem compared to traditional sliding mode control.
Key words: refrigeration system; disturbance observer; non-singular terminal sliding mode control
目前商用空调多采用压缩式制冷机组,制冷机组的设计和选型都是根据最大冷热负荷的计算结果完成的,然而,大部分时间机组工作在部分负荷状态下,运行效率不高[1]。因此,为了实现空调节能,实现对机组精准的温度控制尤为重要。国内外许多学者采用分布参数法等方法对压缩制冷机组的建模进行了研究[2-5]。然而,分布参数模型虽精确度高但计算复杂,当迭代次数过多时解容易发散。因此,近年来出现了很多利用分相区集中参数法建模的方法。在建模过程中存在最主要的问题是模型过于简单或复杂,例如张涵等[6]辨识出的2阶传递函数矩阵是线性的,实际上不符合制冷机组非线性的特性,仅在工作点附近满足一定精度要求;程保华[7]提出的12阶非线性模型,模型精确度较高,但是其状态变量中包含制冷剂物性参数及其导数和一些时间常数较小的状态变量,计算复杂,更难用于控制。在压缩制冷机组的控制方法方面,一般采用PID控制方法[8]。PID控制适用于线性模型,而制冷机组模型本质上非线性,且常规的PID控制方法会使得过热度和蒸发温度产生震荡,其抗扰性能减弱,同时对系统摄动没有较强抑制作用,并不能适应制冷系统自动控制的需求。针对此问题,许多学者对控制方法进行了改进,如内模解耦控制[6]、模糊控制[9]、自适应控制[10]等;然而,大部分方法对模型的精确性要求很高,而制冷机组工作范围广,受外界环境干扰影响大,因此,减少控制对数学模型的依赖性、提高系统鲁棒性十分必要。经典的非线性鲁棒设计工具是滑模控制法(sliding mode control, SMC),该方法具有对系统扰动较好的抑制能力,并且可以保证系统对匹配扰动的鲁棒性。然而,传统的滑模控制具有抖振现象,并且在面对参数摄动和外界扰动时的响应速度有待提高。此外,传统的线性滑模面只具有渐进稳定性,收敛速度较慢,VENKCATARAMAN等[11]提出了terminal滑模法(terminal sliding mode,TSM),该方法具有有限时间收敛性与快速的响应速度等优点,但在某些情况下会出现控制的奇异现象,为此,MINH等[12-13]对此进行了改进,但存在收敛速度在接近滑模面时变得较慢的问题。所以,有必要对TSM进行进一步的改进。近年来,扰动观测器(disturbance observer, DOB)被提出,由于其具有良好的抗扰性以及鲁棒性,在跟踪控制[14]、机器人系统[15]、硬盘驱动控制[16]、飞行器控制[17]等方面得到了广泛的应用,同时,许多学者将扰动观测器与滑模控制方法结合起来[18-19],使得系统具有更好的抗干扰能力和动态性能。目前,该方法在制冷系统上应用较少,为此,本文作者设计了二阶非线性扰动观测器,对传统滑模法进行改进,将扰动估计值融入非奇异terminal滑模控制(non-singular terminal sliding mode control, NTSMC),以增强系统的抗扰性,提高系统的动态响应性能。最后,以本文提出的模型为仿真实验对象,与传统滑模法进行了仿真对比。
1 模型建立
1.1 实验平台
压缩式中央空调测试平台系统主要由压缩式制冷部分和中央空调末端组成。
制冷部分主设备包含压缩机、冷凝器、节流装置、蒸发器。其中节流装置设置有电子膨胀阀、热力膨胀阀和电动针形调节阀3种不同的节流方式,用户可根据需求选择节流装置。
系统装置如图1所示。系统参数如表1所示。
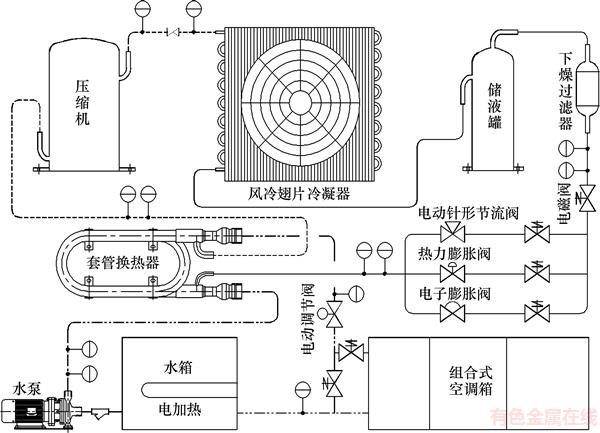
图1 制冷系统装置
Fig. 1 Devices of refrigeration system
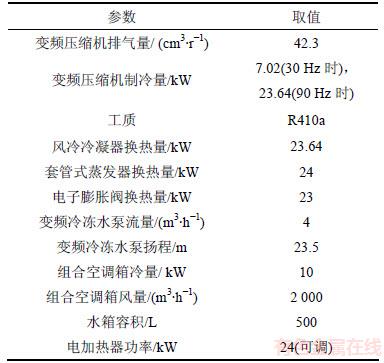
表1 系统参数
Table 1 Parameters of refrigeration system
1.2 换热器建模
在制冷系统运行过程中,电子膨胀阀和压缩机的动态响应远比蒸发器和冷凝器的快,因此,在建模过程中采用稳态建模,而对于动态响应较慢的换热器则采用动态建模。制冷系统的整体模型就由压缩机膨胀阀稳态模型和换热器动态模型组成。
本平台中采用管式换热器的当量直径,将管道看作一维管道。因流体在管道中的流动非常复杂,一般的分区集中参数法均视以下条件为前提:
1) 制冷剂在管内为轴向的一维流动,只考虑换热器的径向传热,忽略轴向传热;
2) 假定每个相区内换热器管壁温度均匀;
3) 忽略换热器管内不凝气体、油膜等对传热的 影响;
4) 换热器在两相区内,采用均相模型,即具有相同的饱和压力和饱和温度,且两相的流动速度相等;
5) 在两相区采用平均空泡系数模型,认为平均空泡系数基本不变;
6) 制冷剂除了在蒸发器和冷凝器的管内有换热外,与管外介质无热交换。
在质量守恒、能量守恒和管壁能量平衡定律的基础上对换热器进行建模。利用分区集中参数法,即将蒸发器内部分为两相区和过热区,分别对2个区域进行集中参数建模。但由于高阶机理模型各变量关系较为复杂,且含有制冷剂物性参数及其偏微分,非常不便于控制器设计。为了获得简化非线性模型,在建模过程中进行如下简化处理:
1) 蒸发器与冷凝器均只考虑两相区;
2) 换热器能量守恒方程只考虑换热器温度的变化,而质量守恒方程只考虑两相区长度的变化;
3) 空隙率、换热系数与制冷剂物性参数均采用 常数。
蒸发器两相区原理图如图2所示。图2中:le为蒸发器两相区长度;Le为蒸发器管道总长度;D为蒸发器当量直径。
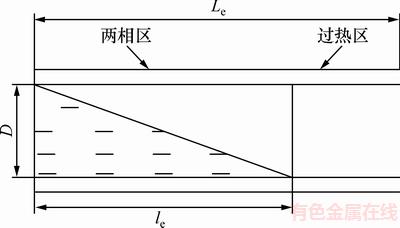
图2 蒸发器相区原理图
Fig. 2 Principle diagram of evaporator zone
简化后的两相区内的制冷剂质量Me和能量Ue分别为:
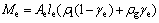 (1)
(1)
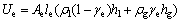 (2)
(2)
式中:γe为空隙率;Ae为蒸发器管道横截面积;ρl和ρg分别为制冷剂饱和液体和蒸汽密度;hl和hg分别为制冷剂饱和液体和蒸汽焓值。
联立式(1)和(2),得
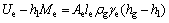 (3)
(3)
这里忽略hl和hg随压力和温度的变化,将式(3)两边同时求导,并进行适当变换,得
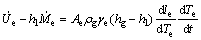 (4)
(4)
再由质量及能量守恒定律可得
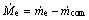 (5)
(5)
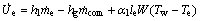 (6)
(6)
式中: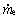 为膨胀阀制冷剂质量流量;
为膨胀阀制冷剂质量流量;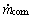 为压缩机制冷剂质量流量;α1为蒸发器中制冷剂与冷冻水换热系数;W为蒸发器管道横截面周长;Te为蒸发温度;Tw为冷冻水温度。
为压缩机制冷剂质量流量;α1为蒸发器中制冷剂与冷冻水换热系数;W为蒸发器管道横截面周长;Te为蒸发温度;Tw为冷冻水温度。
联立式(5)和(6),有
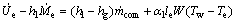 (7)
(7)
根据式(4)和(7),有
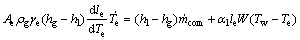 (8)
(8)
将等式两边系数近似为常数,并将等式左边系数化为1,得
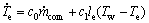 (9)
(9)
然后,将式(1)两端对le求导,并将其代入式(5)得到
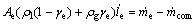 (10)
(10)
将等式左边系数视为常数,则有
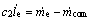 (11)
(11)
式(9)和(11)就是蒸发器的状态方程。
此外,在过热区局部应用能量守恒方程,可估计出过热度:
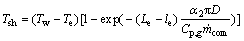 (12)
(12)
式中:α2为过热区换热系数;Cp,g为制冷剂的定压比热容。
同理可得冷凝器的状态方程:
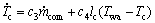 (13)
(13)
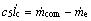 (14)
(14)
式中:Tc为冷凝温度;Twa为冷凝器的管壁温度,为另一个状态变量,可以提高模型精度。根据管壁能量守恒定律,管壁温度变化率可以用管壁吸收制冷剂热功率和向空气散发热功率之和来描述:
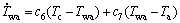 (15)
(15)
式中:c6和c7分别为制冷剂侧和空气侧的换热系数;Ta为环境温度。式(13)~(15)为冷凝器的状态方程。
1.3 压缩机和电子膨胀阀建模
压缩机和电子膨胀阀的参数变化迅速,惯性相对较小,所以可用稳态模型进行建模。这里采用稳态集中参数法建立其数学模型。
压缩机质量流量由以下经验公式表示:
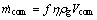 (16)
(16)
式中:f为压缩机频率;η为压缩机效率;Vcom为压缩机理论输气量。
压缩机效率可由下式计算得到:
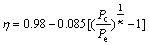 (17)
(17)
式中:Pe和Pc分别为蒸发压力和冷凝压力;κ为多变指数,对于R410a,取κ=1.23[20]。
电子膨胀阀的质量流量可由下式确定:
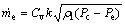 (18)
(18)
式中:Cv为流量系数;k为膨胀阀开度。
1.4 模型验证
针对换热器模型中未知系数,进行最小二乘法辨识,得到的结果如表2所示。
为了验证换热器模型的准确性,在压缩制冷机组平台上进行实验。在压缩制冷系统中,蒸发器过热度、蒸发温度、冷凝温度主要由压缩机质量流量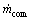 、膨胀阀质量流量
、膨胀阀质量流量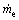 控制,对应的实际控制量分别为压缩机频率f和电子膨胀阀开度k。通过在压缩机频率改变与电子膨胀阀开度变化时测量过热度、蒸发温度和冷凝温度,与模型仿真结果进行对比验证。
控制,对应的实际控制量分别为压缩机频率f和电子膨胀阀开度k。通过在压缩机频率改变与电子膨胀阀开度变化时测量过热度、蒸发温度和冷凝温度,与模型仿真结果进行对比验证。
表2 换热器模型参数
Table 2 Parameters of heat exchanger model

初始条件如下:水箱水温为10.8 ℃,室温为30 ℃,冷冻水流量为4.35 m3/h。压缩机频率为70 Hz,电子膨胀阀开度85%。
在700 s时压缩机频率从70 Hz增加到90 Hz,膨胀阀开度保持不变。结果见图3。
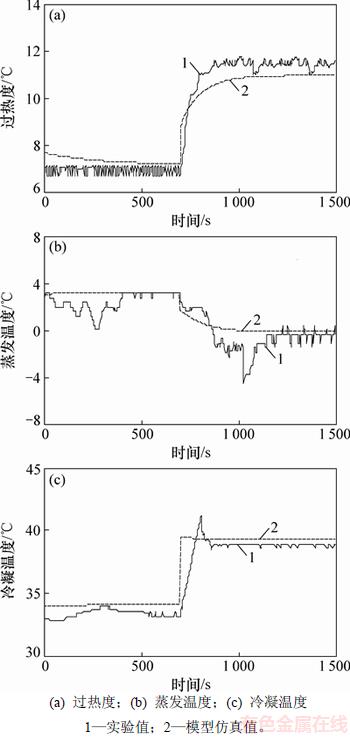
图3 压缩机频率变化时模型验证
Fig. 3 Model validation when frequency of compressor changes
在700 s时,膨胀阀开度从85%减小到55%,压缩机频率保持不变。结果见图4。
通过实验结果与仿真结果对比可以看出:模型具有较小的稳态误差,同时具有一定的动态误差。这是因为实验装置中采用的风冷冷凝器置于室外,受环境条件影响较大;另外,对于模型中各物性参数及换热系数的简化,也会带来一定的精度损失,但总体而言,各温度指标稳态误差在1 ℃之内,模型的动态和稳态精度可以比较准确地描述系统的变化。
图4 膨胀阀开度变化时模型验证
Fig. 4 Model validation when opening of expansion valve changes
2 控制方法
2.1 扰动观测器设计
制冷机组受环境温度、风速和湿度等影响较大,因此对于系统模型,存在模型失配与不确定性扰动。本文针对蒸发器子系统,设计扰动观测器估计复合 扰动。
由于蒸发器子系统中扰动主要存在于蒸发温度,因此根据前面提出的制冷系统模型,带有扰动观测器的蒸发器模型如下式所示:
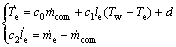 (19)
(19)
式中:d为复合扰动;主要包括未建模动态及参数不确定性、系统进入不稳定工作点带来的参数摄动等。
设计扰动观测器,需进行以下假设。
假设1 蒸发器子系统的复合扰动及其各阶导数是有界的,并且其范数满足:
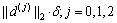
其中:δ>0。
现设计二阶扰动观测器估计复合扰动d。
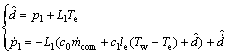 (20)
(20)
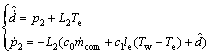 (21)
(21)
式中: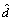 和
和 分别为d和
分别为d和 的估计值;p1和p2为辅助变量;L1和L2为正的常系数。
的估计值;p1和p2为辅助变量;L1和L2为正的常系数。
定理1 二阶扰动观测器的估计误差有界。
证明 定义估计误差为
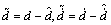
得
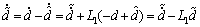 (22)
(22)
同理可得
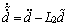 (23)
(23)
定义观测器的误差为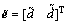 ,易得观测器误差的状态方程为
,易得观测器误差的状态方程为
 (24)
(24)
式中:
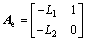 ;
;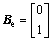
通过选择合适的参数L1和L2使得Ae的特征值位于左半开平面,从而上述误差方程渐进稳定。
选择Lyapunov函数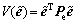 。
。
其中:Pe满足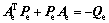 ,Qe为正定阵。
,Qe为正定阵。
对该Lyapunov函数求导得

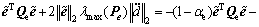
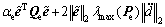 (25)
(25)
式中:0<αe<1。
所以,有
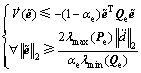 (26)
(26)
另外, 满足不等式
满足不等式
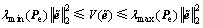
可得最终边界为
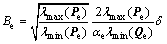 (27)
(27)
证毕。
2.2 非奇异terminal滑模控制器设计
传统滑模控制方法主要问题是控制器输出容易产生抖振现象,不能保证系统在有限时间内收敛到原点。因此,针对上述问题,设计改进的terminal滑模控制器以更好地克服传统滑模控制器的缺点,这里定义扰动观测器估计误差的上确界为
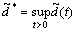
定义蒸发温度误差为
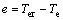 (28)
(28)
式中:Ter为蒸发温度参考值。
定义滑模变量σ=e,控制目标是使蒸发温度较快达到给定值,即使得σ=0。同时,为了更好地利用扰动的导数信息,还设计控制器以使得滑模变量的导数为0,即使得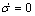 。滑模变量及其二阶导数如下:
。滑模变量及其二阶导数如下:
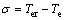 (29)
(29)
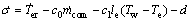 (30)
(30)
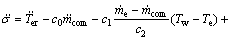
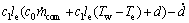 (31)
(31)
系统的相对阶为1,为便于控制器的设计,选取辅助变量y1=σ,y2=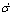 。
。
把二阶滑模的控制问题转换为不确定二阶系统的有限时间稳定问题:
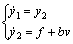 (32)
(32)
式中:f和b(b≠0)是关于y的有界光滑的非线性不确定函数。
在式(32)中,控制量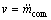 ,而实际的控制量为压缩机频率f,f由
,而实际的控制量为压缩机频率f,f由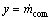 求得,所以,
求得,所以,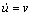 。此二阶滑模系统的控制量是由v通过积分而得的,这样就克服了传统滑模控制作用的不连续性,可以消除抖振。
。此二阶滑模系统的控制量是由v通过积分而得的,这样就克服了传统滑模控制作用的不连续性,可以消除抖振。
现针对系统(32)设计改进的terminal滑模控制器。传统的terminal滑模面如下:
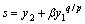 (33)
(33)
式中:β>0;p和q为正奇数,满足1<p/q<2。
存在TSM的充分条件为
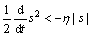 (34)
(34)
式中:η>0。
当系统到达滑模面s=0时,有
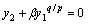 (35)
(35)
即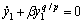 。
。
通过选择合适的控制v使得系统满足条件(34),则系统可在有限时间tr内[21]到达滑模面s=0。在系统到达滑模面后,可以证明y1和y2在有限时间内收敛到0[21]。
传统的滑模控制量选为
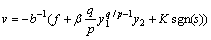 (36)
(36)
式中:K>0。注意到控制项中包含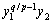 ,当
,当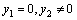 时,
时,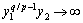 ,形成奇异现象。在理想滑模面上,有
,形成奇异现象。在理想滑模面上,有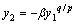 ,将其代入
,将其代入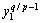 得y2=
得y2=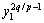 ,因为
,因为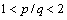 ,所以,
,所以,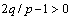 ;当y1=0时,并不会出现奇异现象。但是,由于计算误差和不确定性的影响,保证理想滑模面几乎不可能,因此,只要出现
;当y1=0时,并不会出现奇异现象。但是,由于计算误差和不确定性的影响,保证理想滑模面几乎不可能,因此,只要出现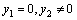 时就会发生奇异现象。因此,采用非奇异terminal滑模法是必要的。
时就会发生奇异现象。因此,采用非奇异terminal滑模法是必要的。
本文提出的非奇异terminal滑模面如下:
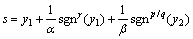 (37)
(37)
式中: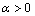 ;
;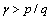 ;
;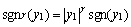 ;
;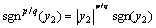 。式(37)中添加了线性项,当接近给定值时可以加快收敛速度。另外,设计
。式(37)中添加了线性项,当接近给定值时可以加快收敛速度。另外,设计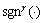 项是为了保证在计算过程中每一项都为实数。
项是为了保证在计算过程中每一项都为实数。
定理2 对于式(37),若控制为
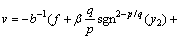
 (38)
(38)
系统能在有限时间内收敛至0。
证明
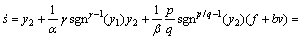
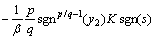 ;
;
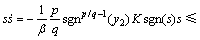
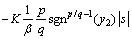 。
。
令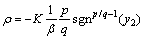 。
。
1) 若 ,则
,则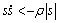 。由于
。由于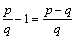 ,
,
其中p-q为偶数,所以,总有ρ>0。此时满足条件(34),系统自然可以在有限时间内到达滑模面。
2) 若y2=0,则有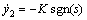 。
。
易证系统同样可在有限时间内到达零点[21-22],同时从控制量中容易看出不包含可能导致奇异的项。
证毕。
现进行控制器的设计,由上述推导,将各变量代入式(38)可得:
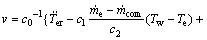
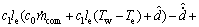
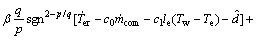
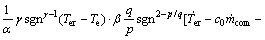
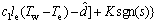 (39)
(39)
得到控制量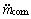 后,对其进行积分可得到实际控制量
后,对其进行积分可得到实际控制量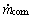 。
。
2.3 传统滑模控制器设计
为了更好地体现本方法的优越性,另设计传统滑模控制方法进行对比。
选择滑模面如下:
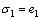 (40)
(40)
对式(40)求导,得
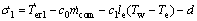 (41)
(41)
设计控制量
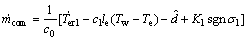 (42)
(42)
式中:K1为正常数。
将式(42)代入式(41),得闭环系统:
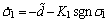 (43)
(43)
根据Lyapunov稳定条件易知,只需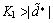 ,滑模变量将会渐进收敛到滑模面σ1=0。
,滑模变量将会渐进收敛到滑模面σ1=0。
3 仿真结果
现以控制制冷机组的蒸发温度为目标,对基于扰动观测器的NTSMC法进行仿真研究。本文设计了3组仿真实验,对控制方法中采用的扰动观测器及NTSMC的控制效果进行验证。
3.1 扰动观测器优越性验证
根据式(16)和(18),压缩机频率和电子膨胀阀开度的改变会引发压缩机质量流量和膨胀阀质量流量的变化,相当于给系统输入端施加了一个复合扰动。在初始条件下,水箱水温为10.8 ℃,室温为30 ℃,冷冻水流量为4.35 m3/h。压缩机频率为70 Hz,电子膨胀阀开度为85%,选取观测器增益L1=8,L2=100。
在膨胀阀开度变化情况下,加入DOB模型与原模型蒸发温度对比见图5。在500 s时,膨胀阀开度从85%阶跃下降为55%,其他条件不变;在1 000 s时,膨胀阀开度从55%变为85%,其他条件不变。
在压缩机频率变化情况下,加入DOB模型与原模型蒸发温度对比见图6。在500 s时,压缩机频率从70 Hz阶跃上升为90 Hz,其他条件不变;在1 100 s时,压缩机频率从90 Hz变为70 Hz,其他条件不变。
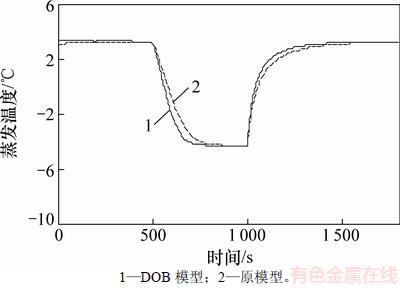
图5 膨胀阀开度变化蒸发温度对比
Fig. 5 Comparison of evaporation temperature when opening of expansion valve changes
由图5和图6可知:与原模型相比,在压缩机频率和膨胀阀开度信号阶跃变化的情况下,加入DOB模型都具有更短的调节时间和更快的收敛速度,其蒸发温度比原模型先到达稳态值。因此,加入DOB可使系统具有更优良的动态性能。图7和图8所示分别为当膨胀阀开度变化和压缩机频率变化时DOB模型估计出的复合扰动值。从图7和图8可以看出:当膨胀阀开度于500 s和1 000 s阶跃变化时,观测器均迅速反应,扰动估计值随开度信号变化,并在300 s内稳定;当压缩机频率于500 s和1 100 s阶跃变化时,观测器均迅速反应,估计值均在400 s内稳定。因此,加入DOB对于系统扰动有较快的响应和计算速度。
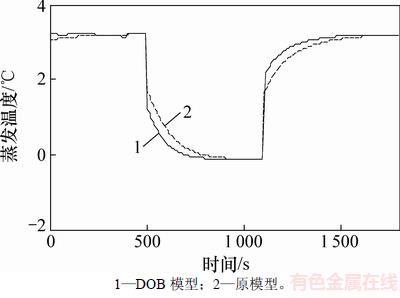
图6 压缩机频率变化蒸发温度对比
Fig. 6 Comparison of evaporation temperature when frequency of compressor changes
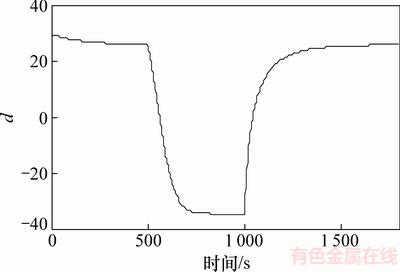
图7 膨胀阀开度变化时DOB模型扰动估计
Fig. 7 Estimation of disturbance as opening of expansion valve changes
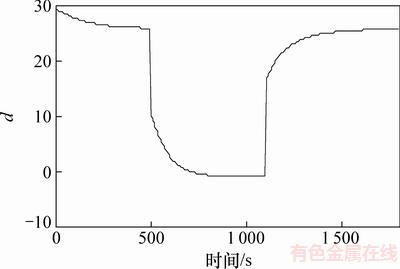
图8 压缩机频率变化时DOB模型扰动估计
Fig. 8 Estimation of disturbance when frequency of compressor changes
3.2 NTSMC法优越性验证
蒸发温度初始参考值为8.5 ℃。在200 s时,将蒸发温度参考值设为6 ℃,其他条件不变;在600 s时,将蒸发温度参考值设为8.5 ℃,其他条件同样不变。选取α=2,β=1,γ=3,p=5,q=3,K=5,K1=2,扰动观测器的参数选取同上,蒸发温度对比见图9。
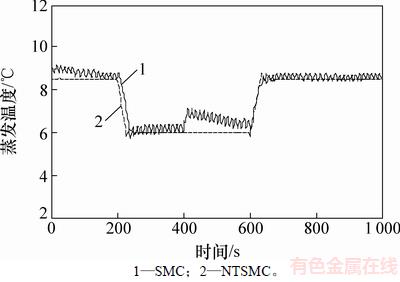
图9 SMC与NTSMC下蒸发温度对比
Fig. 9 Comparison of evaporation temperature under SMC and NTSMC
从图9可以看出:NTSMC在给定值阶跃变化后很快进入稳态,而SMC的调节时间较长,且存在比较明显的抖振现象,在给定值附近波动。因此,NTSMC法在调节速度和稳态误差方面都具有比较明显的优势,而且不存在传统滑模存在的抖振问题。SMC与NTSMC下控制量曲线对比见图10。
从图10可以看出,NTSMC控制量无抖动,并且没有明显的波动;SMC法在400 s左右出现了明显的波动,蒸发温度也发生了较大的波动,可能的原因是选择了固定的控制器增益值,不能很好地适应系统变化情况。因此,NTSMC法可以得到更稳定的控制量输出。
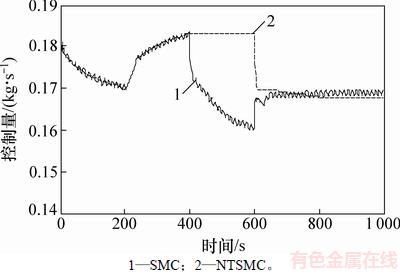
图10 SMC与NTSMC下控制量对比
Fig. 10 Comparison of controlled variable under SMC and NTSMC
3.3 NTSMC抗扰性检验
在初始条件下,压缩机频率为70 Hz,膨胀阀开度为85%,在100 s时,给蒸发器系统控制输入端一加性阶跃扰动d=0.1,控制器其他参数选取同上,蒸发温度对比如图11所示。
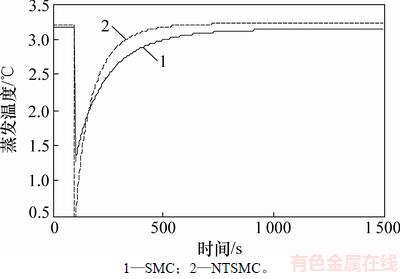
图11 SMC与NTSMC抗扰性检验
Fig. 11 Disturbance rejection tests of SMC and NTSMC
由图11可见,NTSMC法蒸发温度受阶跃扰动后下降,随即迅速上升,并在700 s时到达稳态值;而SMC法蒸发温度虽受扰动下降幅度略小于前者,但调节速度明显慢于前者,在1 000 s时才到达稳态。因此,总体来看,NTSMC法具有更好的抗扰性和更快的调节速度。
4 结论
1) 在模型建立方面,经过合理假设和对换热系数以及制冷剂物性参数的简化,通过机理建模结合实验辨识求得制冷机组五阶模型,并由仿真与实验结果对比,验证了模型良好的精确性。
2) 在控制方法方面,通过结合扰动观测器和二阶terminal滑模法对所提出的模型进行控制。设计了二阶扰动观测器,并证明了扰动估计误差的有界性,计算了误差的最终边界;针对传统的滑模控制易产生抖振的现象和较慢的收敛速度,在二阶滑模系统的基础上采用terminal非线性滑模面,并分析了TSM控制中可能出现的奇异现象,针对此现象提出了NTSM法;将控制量设计为实际控制量的导数,这样在计算实际控制量时由于积分的作用,消除了传统滑模中的抖振问题。通过与基于扰动观测器的传统滑模法的对比仿真,验证了NTSM法具有更好的抗扰性和更快的动态响应速度。
参考文献:
[1] 江亿. 我国建筑耗能状况及有效的节能途径[J]. 暖通空调, 2005, 35(5): 30-40.
JIANG Yi. Current building energy consumption in China and effective energy efficiency measures[J]. Journal of HV&AC, 2005, 35(5): 30-40.
[2] DING Guoliang. Recent developments in simulation techniques for vapour-compression refrigeration systems[J]. International Journal of Refrigeration, 2007, 30(7): 1119-1133.
[3] JIA X, TSO C P, JOLLY P, et al. Distributed steady and dynamic modeling of dry-expansion evaporators[J]. International Journal of refrigeration, 1999, 22(2): 126-136.
[4] WANG S, WANG J. Mechanistic model of centrifugal chillers for HVAC system dynamics simulation[J]. Building Services Engineering Research and Technology, 2000, 21(2): 73-83.
[5] 葛云亭, 彦启森. 蒸发器动态参数数学模型的建立与理论计算[J]. 制冷学报, 1995, 16(1): 9-17.
GE Yunting, YAN Qisen. Foundation of dynamic parameter model and theoretical calculation of evaporator[J]. Journal of Refrigeration, 1995, 16(1): 9-17.
[6] 张涵, 吴爱国, 杨硕, 等. 变频压缩式制冷系统的内模解耦控制策略[J]. 控制理论与应用, 2014, 31(1): 120-127.
ZHANG Han, WU Aiguo, YANG Shuo, et al. Internal model decoupling control strategy of variable frequency compression refrigeration system control[J]. Control Theory & Applications, 2014, 31(1): 120-127.
[7] 程保华. 制冷系统动态建模及优化控制方法研究[D]. 天津: 天津大学电气与自动化工程学院, 2013: 28-49.
CHENG Baohua. Dynamic modeling of refrigeration system and research on optimization control method[D]. Tianjin: Tianjin University. School of Electrical Engineering & Automation, 2013: 28-49.
[8] YASUDA H, ISHIBANE K, NAKAYAMA S. Evaporator superheat control by an electrically driven expansion valve[J]. Transactions of the Japan Society of Refrigerating and Air Conditioning Engineers, 2011, 9(2): 147-156.
[9] 由玉文, 吴爱国, 翟文鹏. 变负荷工况下制冷系统多变量模糊控制方法研究[J]. 制冷技术, 2011, 39(12): 45-49.
YOU Yuwen, WU Aiguo, ZHAI Wenpeng. Multivariable fuzzy control of the refrigeration system based on varying load[J]. Chinese Journal of Refrigeration Technology, 2011, 39(12): 45-49.
[10] RASMUSSEN H, LARSEN L F S. Non-linear and adaptive control of a refrigeration system[J]. IET Control Theory & Applications, 2011, 5(2): 364-378.
[11] VENKCATARAMAN S T, GULATI S. Control of nonlinear systems using terminal sliding modes[J]. Journal of Dynamic Systems, Measurement and Control, 1993, 115(3): 554-560.
[12] MINH D T, HEE J K. Nonsingular terminal sliding mode control of uncertain second-order nonlinear systems[J]. Mathematical Problems in Engineering, 2015: 10.1155/2015/181737.
[13] FENG Y, YU X H, HAN F L. On nonsingular terminal sliding-mode control of nonlinear systems[J]. Automatica, 2013, 49(6): 1715-1722.
[14] KEMPF C J, KOBAYASHI S. Disturbance observer and feedforward design for a high-speed direct-drive position table[J]. IEEE Transactions on Control Systems Technology, 1999,7(5): 513-526.
[15] CHEN W H, GAWTHROP P J, REILLY J O. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938.
[16] THUM C K, DU C, LEWIS F L, et al. H-infinity disturbance observer design for high precision track following in hard disk drives[J]. IET Control Theory & Applications, 2009, 3(12): 1591-1598.
[17] GUO L, CHEN W H. Disturbance attenuation and rejection for systems with nonlinearity via DOBC approach[J]. International Journal of Robust and Nonlinear Control, 2005, 15(3): 109-125.
[18] CHEN Xinkai. A nonlinear exact disturbance observer inspired by sliding mode techniques[J]. Mathematical Problems in Engineering, 2015(1): 1-6.
[19] LI H R, JIANG Z B, KANG N. Sliding mode disturbance observer-based fractional second-order nonsingular terminal sliding mode control for PMSM position regulation system[J]. Mathematical Problems in Engineering, 2015(5): 1-15.
[20] 秦振春. R410A空气源热泵工作过程仿真及实验研究[D]. 南京: 南京师范大学动力工程学院, 2007: 18-19.
QIN Zhenchun. Simulation and experimental research of air-source heat pump with the refrigerant R410A[D]. Nanjing: Nanjing Normal University. College of Power Engineering, 2007: 18-19.
[21] FENG Y, YU X H, HAN F L. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167.
[22] XU S D, CHEN C C, WU Z L. Study of nonsingular fast terminal sliding-mode fault-tolerant control[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3906-3913.
(编辑 赵俊)
收稿日期:2017-06-16;修回日期:2017-08-23
基金项目(Foundation item):国家自然科学基金资助项目(61403274,51337007);天津市应用基础及前沿技术研究计划项目(13JCQNJC03600) (Projects(61403274, 51337007) supported by the National Natural Science Foundation of China; Project(13JCQNJC03600) supported by the Application Base and Frontier Technology Research Program of Tianjin of China)
通信作者:吴爱国,教授,博士生导师,从事制冷系统、电气液压和飞行器等控制算法的研究;E-mail:wuaiguotju@163.com