数控机床主轴系统可靠性评价
谷东伟,申桂香,张英芝,王志琼,陈炳锟,郑珊
(吉林大学 机械科学与工程学院,吉林 长春,130022)
摘要:以40台某国产数控机床主轴系统现场试验数据为基础,针对数控机床主轴系统故障数据少,导致截尾时间所占比重比较大的特点,为提高建模的准确性,采用故障总时间法对数据进行预处理,通过参数估计、d检验和游程检验确定故障过程服从二参数威布尔分布;针对某些样本无故障的特点,采用平均秩次法评估影响顾客满意度的指标即平均首次故障时间。针对主轴系统的故障特点,采用以上方法能够得到更精确的可靠性评价指标。
关键词:主轴系统;故障总时间法;平均首次故障时间;游程检验
中图分类号:TG659;TB114.3 文献标志码:A 文章编号:1672-7207(2013)02-0540-06
Reliability evaluation of spindle system of CNC
GU Dongwei, SHEN Guixiang, ZHANG Yingzhi, WANG Zhiqiong, CHEN Bingkun, ZHENG Shan
(College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China)
Abstract: On the basis of failure data gathered from forty spindle systems of CNC for evaluating the reliability of spindle system of CNC,because of few data of spindle system, resulting in a relatively large proportion censored time, it is difficult to evaluate, for enhancing the accuracy of the modeling, the total failure time method was used for data pre-processing, then a two-parameter Weibull distribution model which passed d test and Heteroscedasticity testing was established. Because some samples have no fault, mean rank order method was used to assess the impact on average customer satisfaction index—mean time to first failure. The results show that with the failure characteristics of the spindle system, using this method can get more accurate reliability evaluation.
Key words: spindle system; total fault time method; mean time to first failure; run test
主轴系统作为数控机床的关键子系统,一旦发生故障,机床将无法正常工作,主轴系统的可靠性对数控机床整机可靠性的影响较为严重[1-2]。工程或试验中如何对主轴进行可靠性评价是目前亟待解决的问题。当前对主轴系统的研究主要侧重于主轴动态特性[3-5]、轴承[6-7]及热补偿[8-9]等性能方面,而很少针对主轴系统可靠性进行研究。数控机床主轴系统的可靠性试验是有替换的定时截尾试验,但由于投入使用的时间不同,导致数据出现随机截尾的特征[10]。本次参加试验的数控机床主轴系统较多,截尾数据也较多,还有很多主轴系统在试验周期中没有发生故障,所以,试验获得的故障数据很少,在此情况下如何提高建模的准确性和评估主轴系统平均首次故障时间一直是可靠性评定的焦点。本文作者通过对国产某型号主轴系统进行现场跟踪记录,获得真实可靠的故障数据。在故障数据的基础上,针对某些样本没发生故障,导致截尾时间所占比例较大的特点,引入故障总时间的概念,并通过平均秩次法和最小二乘法进行参数估计;针对某些样本无故障数据的特性,为得到主轴系统的平均首次故障时间,采用平均秩次法对主轴首次故障时间进行评估。通过上述2种方法既可以提高计算的精度和速度,又可以提高主轴可靠性评价的精确性。
1 可靠性建模
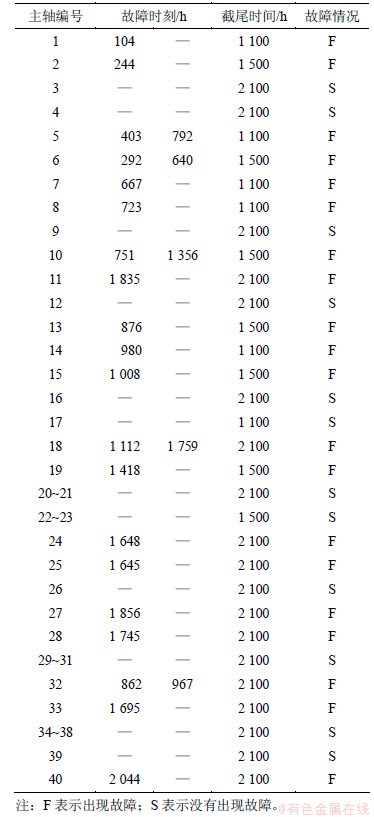
针对40台某型号国产数控机床主轴系统进行现场定时截尾试验,记录主轴系统的故障发生时间。由于考核的起始时间不同,主轴系统的考核时间呈现随机截尾的特性。本次试验的故障数据见表1。
表1 主轴系统故障数据表
Table 1 Failure data of spindle system
1.1 故障总时间法
为获得更高的评估精度,针对主轴系统故障数据的特点,本文采用故障总时间法进行数据预处理。故障总时间的计算方法如图1所示[11]。以3台主轴系统进行可靠性试验为例,tks为第k号(k=1,2,3)主轴系统试验截止时间,“·”表示故障点。各故障点的故障总时间计算方法为
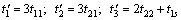 (1)
(1)
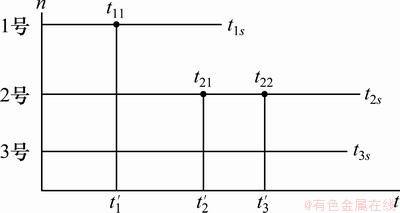
图1 故障总时间的计算方法
Fig.1 Calculation method of total fault time
1.2 数据处理及参数估计
对每台主轴系统发生故障的时间按从小到大的顺序进行排列,按图1所示的方法计算故障总时间tk′,则故障间隔时间△ti为
 (2)
(2)
对存在截尾数据的试验数据进行可靠性建模,需要对其故障顺序进行重新排号。故障间隔时间的排号用文献[12]中的平均秩次法。第i个故障数据的故障顺序号ri的计算公式如下:
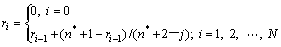 (3)
(3)
式中:n*=N+1,N为故障总数;j为N个故障数据加上截尾数据后的从小到大排列顺序号;i为N个故障数据从小到大的排列顺序号。
故障间隔时间的F(t)用中位秩进行计算:
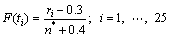 (4)
(4)
由式(1)~(4)以及表1中的数据计算得到的故障间隔时间Δti和经验分布函数F(ti)见表2。根据以往对主轴数据的统计可知:主轴的故障间隔时间符合威布尔分布,△ti的威布尔概率纸图(WPP图)如图2所示。
两参数的威布尔分布的公式为:
表2 主轴系统的故障时间统计表
Table 2 Failure time statistical of spindle system
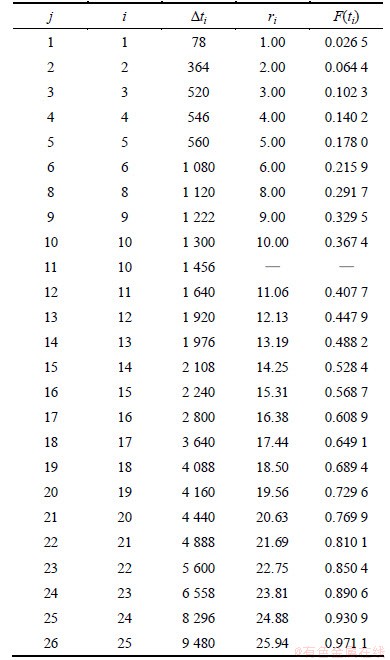
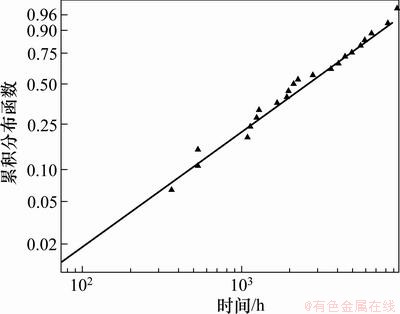
图2 △ti的WPP图
Fig.2 WPP of △ti
 (5)
(5)
根据表2中的数据,采用文献[13]中最小二乘法对威布尔分布进行参数估计得到:形状参数β=1.06,尺寸参数α=3 124。
1.3 拟合优度检验
对于小样本的情况我们通常采用d检验法进行检验。d检验法是将n个试验数据按由小到大的次序排列,根据假设的分布,计算每个数据对应的F0(xi),将其与经验分布函数Fn(xi)进行比较,得到检验统计量Dn的观察值如下:
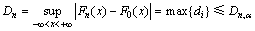 (6)
(6)
式中:Dn,α为临界值,当α=0.1时,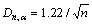 ;F0(x)为原假设分布函数;Fn(x)为样本为n的经验分布函数,将Dn与临界值Dn,α进行比较,若满足条件Dn,α>Dn,则接受原假设,否则,拒绝原假设。通过计算可求得:Dn,α=0.25;Dn=0.09。由于Dn,α>Dn,故接受原假设,认为此型号主轴系统的故障间隔时间符合威布尔分布。
;F0(x)为原假设分布函数;Fn(x)为样本为n的经验分布函数,将Dn与临界值Dn,α进行比较,若满足条件Dn,α>Dn,则接受原假设,否则,拒绝原假设。通过计算可求得:Dn,α=0.25;Dn=0.09。由于Dn,α>Dn,故接受原假设,认为此型号主轴系统的故障间隔时间符合威布尔分布。

1.4 异方差检验
为保证故障数据符合所假设的模型,本文对故障时间的样本值进行游程检验。在进行游程检验之前,先介绍几个相关的概念。
游程:连续出现具有相同特征的样本点为一个游程。
游程数用R来表示,游程数的分布为:
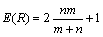 (7)
(7)
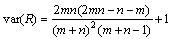 (8)
(8)
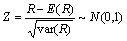 (9)
(9)
式中:R为游程数;n为序列中0的个数;m为数列中1的个数。游程检验的步骤如下。
步骤1 求出故障间隔时间的经验分布函数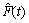 和F(t)的残差
和F(t)的残差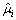 ,则可得残差
,则可得残差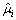 按下标i取值排列的1个数列。其中
按下标i取值排列的1个数列。其中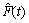 由近似中位秩公式
由近似中位秩公式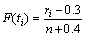 获得。
获得。
步骤2 将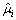 取绝对值|
取绝对值|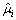 |,同时将|
|,同时将|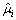 |按递升或递降次序排列,求出该排列的中位数μ*=0.016。
|按递升或递降次序排列,求出该排列的中位数μ*=0.016。
步骤3 将数列中各个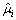 取绝对值,但保持原序列的顺序不变,并用
取绝对值,但保持原序列的顺序不变,并用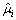 的绝对值|
的绝对值|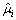 |去减μ*,若得正值|
|去减μ*,若得正值|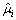 |>μ*则记为1;若得负值,则|
|>μ*则记为1;若得负值,则|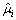 |<μ*,记为0。就可得一组由0和1组成的序列。该序列中0表示在该位置上的绝对值|
|<μ*,记为0。就可得一组由0和1组成的序列。该序列中0表示在该位置上的绝对值|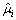 |小于中位数μ*,1则表示在该位置上的|
|小于中位数μ*,1则表示在该位置上的|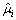 |大于μ*的中位数μ*。对|
|大于μ*的中位数μ*。对|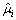 |-μ*,运用步骤3的判断原则可以得到游程序列:011011011001111110000000。序列的游程数为8。由式(7)和(8)计算得到:
|-μ*,运用步骤3的判断原则可以得到游程序列:011011011001111110000000。序列的游程数为8。由式(7)和(8)计算得到:
E(R)=13 var(R)=6.74
步骤4 对序列进行游程检验。观察序列的游程数R,将计算的数据代入式(9)得到:
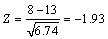
Z渐进服从于N(0,1)分布。在给定显著行水平α=0.01时,查正态分布表[14]可以得到临界值D=2.33。因为|Z|<D,本文的故障数据的序列通过随机游程检验,故障数据不存在异方差,说明采用故障总时间法和最小二乘法获得的参数较精确。通过上拟合优度检验和异方差检验,可以确定此主轴系统的故障间隔时间符合二参数威布尔分布,其分布函数和可靠度函数如下:
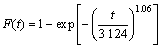
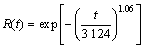
该主轴系统的可靠度曲线如图3所示。
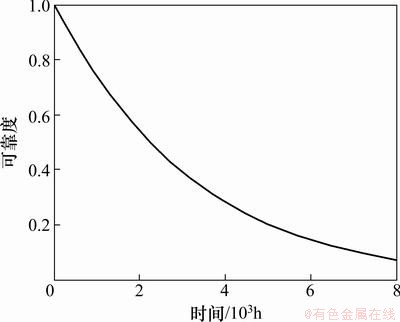
图3 R(t)的曲线
Fig.3 Curve of R(t)
2 平均首次故障时间
首次故障时间是产品首次进入可用状态直至首次故障发生的总持续工作时间,是顾客满意度的一个重要指标。平均首次故障时间是描述可修系统首次故障状况的一个可靠性特征量,它相当于不可修产品的寿命问题[15]。平均首次故障时间即首次故障前时间的期望值,常用MTTFF(Mean time to first failure)表示。首次故障时间的可靠性评价的实质是主轴系统质量的度量与评价。
这里将40台主轴系统的首次故障发生时间按大小排列,如表1所示,出现故障的用F表示,没有出现故障的用S表示。上述情况既可以采用残存比率法分析,也可以采用平均秩次法分析,但残存比率法适用于样本量较大的情况,而平均秩次法采用中位秩且适用于样本量较小的情况。针对可靠性试验中出现的随机截尾特性和部分样本无故障数据等特点,本文采用平均秩次法确定经验分布函数,利用线性回归分析方法进行参数估计,采用d检验法进行拟合性检验,通过游程检验进行异方差检验。
平均秩增量公式[16]为
 (10)
(10)
平均秩公式为
 (11)
(11)
式中:Ak为故障产品的平均秩次;k为故障产品的顺序号;Ak-1为前一个故障产品的平均秩次;A0=0;i*为所有产品的排列顺序号,按所有时间的大小排序。
将平均秩次代入中位秩公式中计算产品的经验分布函数:
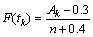 (12)
(12)
下面用式(11)和(12)计算表1中20台出现故障主轴系统的首次故障时间的平均秩次和经验分布函数,结果如表3所示。
根据表3中数据,采用文献[13]中最小二乘法对威布尔分布进行参数估计得到:β=1.231,α=2 906。
同样对其进行d检验和异方差检验。当α=0.1时,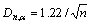 。通过计算可求得:Dn,α=0.27;Dn=0.06。因为Dn,α>Dn,故接受原假设,认为此型号主轴的首次故障时间符合威布尔分布。采用上面的方法得到游程序列为01001111000011000111,游程数为7,由式(7)~(9)得到:
。通过计算可求得:Dn,α=0.27;Dn=0.06。因为Dn,α>Dn,故接受原假设,认为此型号主轴的首次故障时间符合威布尔分布。采用上面的方法得到游程序列为01001111000011000111,游程数为7,由式(7)~(9)得到: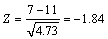 。
。
表3 主轴系统首次故障时间的经验分布函数
Table 3 MTTFF experience distribution function of spindle system

在给定显著行水平α=0.01时,查正态分布表可以得到临界值D=2.33。因为|Z|<D,故本文的故障数据的序列通过随机游程检验,故障数据不存在异方差,说明采用此方法估计的参数较精确。可以确定此主轴系统的故障间隔时间符合二参数威布尔分布,其分布函数和可靠度函数如下:
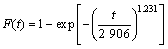
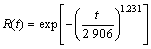
则平均首次故障时间为
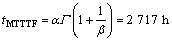
3 结论
(1) 针对可靠性试验中出现的随机截尾特性和部分样本无故障数据等特点,采用故障总时间法进行数据处理和可靠性建模。此种方法充分利用了截尾信息,使分析精度更高。
(2) 采用平均秩次法建立主轴系统的首次故障时间模型,获得主轴系统的平均首次故障时间,对主轴系统进行了综合的质量评价。
(3) 通过对主轴系统的可靠性评定,为主轴系统设计以及主轴系统可靠性增长提供了依据。
参考文献:
[1] 贾亚洲, 杨兆军. 数控机床可靠性国内外现状与技术发展策略[J]. 中国制造业信息化, 2008(8): 35-37.
JIA Yazhou, YANG Zhaojun. Home and abroad status for NC machine tool reliability and technology development strategy[J]. Manufacture Information Engineering of China, 2008(8): 35-37.
[2] Schwallie B. 主轴技术进步促进提高生产率、可靠性、性能和设计寿命[J]. 世界制造技术与市场, 2004(2): 50-52.
Schwallie B. Advances in spindle technologies lead to increases in productivity reliability, performance and design life[J]. World Manufacturing Engineering & Market, 2004(2): 50-52.
[3] CHEN Dongju, FAN Jinwei, ZHANG Feihu. Dynamic and static characteristics of a hydrostatic spindle for machine tools[J]. Journal of Manufacturing Systems, 2012, 31(1): 26-33.
[4] Gagnol V, Le T P, Ray P. Modal identification of spindle-tool unit in high-speed machining[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2388-2398.
[5] Gagnol V, Bouzgarrou B C, Ray P, et al. Model-based chatter stability prediction for high-speed spindles[J]. International Journal of Machine Tools & Manufacture, 2007, 47(7/8): 1176-1186.
[6] LIN Chiwei, Tu J F. Model-based design of motorized spindle systems to improve dynamic performance at high speeds[J]. Journal of Manufacturing Process, 2007, 9(2): 94-108.
[7] JIANG Shuyun, MAO Hebing. Investigation of variable optimum preload for a machine tool spindle[J]. International Journal of Machine Tools & Manufacture, 2010(5): 19-28.
[8] WANG Yungcheng, KAO Mingche, CHANG Chungping. Investigation on the spindle thermal displacement and its compensation of precision cutter grinders[J]. Measurement, 2011, 44(6): 1183-1187.
[9] ZHAO Haitao, YANG Jianguo, SHEN Jinhua. Simulation of thermal behavior of a CNC machine tool spindle[J]. International Journal of Machine Tools & Manufacture, 2007, 47(6): 1003-1010.
[10] 张英芝, 申桂香, 吴甦, 等. 随机截尾数控机床三参数威布尔分布模型[J].吉林大学学报: 工学版, 2009, 39(2): 378-381.
ZHANG Yingzhi, SHEN Guixiang, WU Su, et al. 3-parameter Weibull distribution for random truncated NC machine tool fault data[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(2): 378-381.
[11] 王秉刚. 汽车可靠性工程方法[M]. 北京: 机械工业出版社, 1991: 32-35.
WANG Binggang. Auto reliability engineering[M]. Beijing: China Machine Press, 1991: 32-35.
[12] 蒋仁言, 左明建. 可靠性模型与应用[M]. 北京: 机械工业出版社, 1999: 24-27.
JIANG Renyan, ZUO Mingjian. Reliability model and application[M]. Beijing: China Machine Press, 1999: 24-27.
[13] 李研. 国内外数控车床可靠性对比分析[D]. 长春: 吉林大学机械科学与工程学院, 2006: 11-13.
LI Yan. Domestic and foreign-made CNC lathe reliability contrast analysis[D]. Changchun: Jilin University. College of Mechanical Science and Engineering, 2006: 11-13.
[14] 茆诗松, 汤银才, 王玲玲. 可靠性统计[M]. 北京: 高等教育出版社, 2008: 416-417.
MAO Shisong, TANG Yincai, WANG Lingling. Reliability statistical[M]. Beijing: Higher Education Press, 2008: 416-417.
[15] 敖长林, 乔金友, 戴有忠. 威布尔过程场合下现场可靠性试验的统计分析[J]. 东北农业大学学报, 2000, 31(3): 303-306.
AO Changlin, QIAO Jinyou, DAI Youzhong. Statistical analysis of the field credibility test under the situation of weibull process[J]. Journal of Northeast Agricultural University, 2000, 31(3): 303-306.
[16] 贺国芳. 可靠性数据的收集与分析[M]. 北京: 国防工业出版社, 1995: 44-47.
HE Guofang. Reliability data collection and analysis[M]. Beijing: National Defense Industrial Press, 1995: 44-47.
(编辑 杨幼平)
收稿日期:2012-01-12;修回日期:2012-03-20
基金项目:国家科技重大专项(2010ZX04014-011)
通信作者:张英芝(1970-),女,辽宁铁岭人,博士,副教授,从事数控机床可靠性研究;电话:15843078763;E-mail:zhangyz@jlu.edu.cn