J. Cent. South Univ. (2012) 19: 2231-2237
DOI: 10.1007/s11771-012-1267-z
Near-duplicate document detection with improved similarity measurement
YUAN Xin-pan(袁鑫攀), LONG Jun(龙军), ZHANG Zu-ping(张祖平), GUI Wei-hua(桂卫华)
School of Information Science and Engineering, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: To quickly find documents with high similarity in existing documentation sets, fingerprint group merging retrieval algorithm is proposed to address both sides of the problem: a given similarity threshold could not be too low and fewer fingerprints could lead to low accuracy. It can be proved that the efficiency of similarity retrieval is improved by fingerprint group merging retrieval algorithm with lower similarity threshold. Experiments with the lower similarity threshold r=0.7 and high fingerprint bits k=400 demonstrate that the CPU time-consuming cost decreases from 1 921 s to 273 s. Theoretical analysis and experimental results verify the effectiveness of this method.
Key words: similarity estimation; near-duplicate document detection; fingerprint group; Hamming distance; minwise hashing
1 Introduction
Explosive information growth of Web leads to a huge amount of similar information on the Web. These similar documents consumed a lot of storage and computation resources and reduce the efficiency of web search engines. Some duplications come from plagiarism and illegal proliferation. Near-duplicate document detection in intellectual property protection and information retrieval has important applications and plays an important role in efficient information assessment.
The purpose of this system is to avoid near-duplicate submissions (e.g., a financed proposal might be resubmitted without considerable modification). With rapid increment in the number of financed projects, the size of project collection might reach several millions. For such a large text collection, minwise hashing [1-3] is a mature and stable document similarity estimation technique. Minwise hashing converts the set intersection problem into the probability of occurrence of an event to estimate the similarity between the documents through a large number of experiments. As a general technique for estimating set similarity, minwise hashing has been applied to a wide range of applications, for example, duplicate web pages removal [2-3], wireless sensor networks [4], community extraction and classification in the Web graph [5], text reuse in the Web [6], Web graph compression [7] and so on. Due to its wide adoption, minwise hashing has undergone considerable theoretical and methodological developments [8-15].
Two near documents can be easily detected by common similarity estimation algorithms. However, difficulty may rise as the number of documents to be detected is enormous. A near-duplicate documents system faces a number of challenges. First and foremost is the issue of scale: millions of project documents. Second, the system should be able to detect the rapidly increased number of newly added projects per year. So the decision to mark a newly project document as a near-duplicate of an existing document should be made quickly.
Hamming code fingerprint estimation technique [9] is proposed based on the minwise hashing. In a similar way, b-bit minwise hashing [10] can gain substantial advantages in terms of computational efficiency and storage space by only storing the lowest b bits of each (minwise) hashed value (e.g., b=1 or 2). Using Hamming fingerprint characterization of the document, a technique [16] to retrieve similar web-pages under conditions of high similarity threshold is proposed to develop an efficient method for solving the Hamming distance problem in billions of web-pages. There is an obvious shortcoming:the similarity threshold r could not be reduced. While fingerprint bits k is small and the similarity threshold r is reduced, the variance of the original similarity estimation algorithm increases, resulting in the need to improve k to enhance the precision and recall. If k increases, time complexity of the algorithm in Ref. [16] dramatically increases. Fingerprint group merging retrieval algorithm is proposed to address this deficiency. Theoretical analysis and a large number of experiments are carried out to verify the effectiveness of this method.
2 Hamming fingerprint
Estimating the size of set intersections [1] is a fundamental problem in information retrieval, databases, and machine learning. There are two shingles sets S1, S2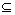 Ω, where Ω={0, 1, …, D-1}, by shingling document D1, D2. Resemblance R(1,2) of document S1 and S2 is R(1, 2)=|S1
Ω, where Ω={0, 1, …, D-1}, by shingling document D1, D2. Resemblance R(1,2) of document S1 and S2 is R(1, 2)=|S1 S2|/|S1
S2|/|S1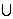 S2|=a/(f1+f2-a), where f1=|S1|, f2=|S2|, a=|S1
S2|=a/(f1+f2-a), where f1=|S1|, f2=|S2|, a=|S1 S2|. After k minwise independent random permutations, denoted by π1, π2, …, πk, where π·Ω→Ω, one can estimate R without bias, as a binomial probability, i.e. an elementary probability argument can show
S2|. After k minwise independent random permutations, denoted by π1, π2, …, πk, where π·Ω→Ω, one can estimate R without bias, as a binomial probability, i.e. an elementary probability argument can show
 (1)
(1)
Hence, by choosing k independent random permutations π1, π2, …, πk, each document D is converted into the list:
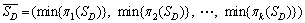
An unbiased estimator of R is denoted by 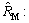
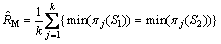 (2)
(2)
 (3)
(3)
Example 1 explains the process of minwise hashing.
Example 1: Let Ω={1, 2, 3, 4, 5, 6}, S1={1, 2, 4}, S2={2, 3, 4, 5}. Choose k=5 minwise independent random permutations: p1{1, 2, 3, 4, 5, 6}→{6, 3, 5, 4, 2, 1}; p2{1, 2, 3, 4, 5, 6}→{4, 1, 2, 6, 5, 3}; p3{1, 2, 3, 4, 5, 6}→{5, 6, 3, 1, 2, 4}; p4{1, 2, 3, 4, 5, 6}→{2, 5, 3, 4, 1, 6}, …, pk{1, 2, 3, 4, 5, 6 }→{5, 2, 6, 4, 3, 1}. So p1(S1)={6, 3, 4}; p2(S1)={4, 1, 6}; p3(S1)={5, 6, 1}; p4(S1)={2, 5, 4}; pk(S1)={5, 2, 4}; p1(S2)={3, 5, 4, 2}; p2(S2)={1, 2, 6, 5}; p3(S2)={6, 3, 1, 2}; p4(S2)={5, 3, 4, 1}; pk(S2)={2, 6, 4, 3}.
S1 can be represented as 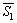 and S2 can be represented as
and S2 can be represented as 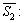
 =
=
{3, 1, 1, 2, 2};
 =
=
{2, 1, 1, 1, 2}
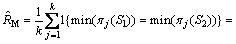 3/5. R=
3/5. R=
|S1 S2|/|S1
S2|/|S1 S2|=2/5. The reason why estimated value
S2|=2/5. The reason why estimated value 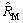 is not equal to the true value of R is that k is too small. If k is small, the variance is large. With the larger k, the estimated value will be closer to true value of R.
is not equal to the true value of R is that k is too small. If k is small, the variance is large. With the larger k, the estimated value will be closer to true value of R.
Based on the minwise hashing, Hamming code fingerprint estimation techniques are proposed in Ref. [9]. Let b be a pairwise independent family of hash functions that operate on the domain of the functions in F and map elements in the domain to {0, 1}. Then Pr{b(u)=b(v)}= 1/2 if u≠v and Pr{b(u)=b(v)}=1 if u=v. With probability R(1,2), min{π(S1)}=min{π(S2)} and hence b(min{π(S1)})=b(min{π(S2)}). With probability 1-R(1,2), min{π(S1)}≠min{π(S2)} and in this case, Pr(b(min{π(S1)})=b(min{π(S2)}) )=1/2. Thus,
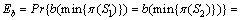
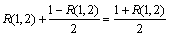 (4)
(4)
An unbiased estimator of R is denoted by 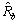 :
:
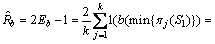
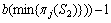 (5)
(5)
Because Eb is binomial distribution, the variance of 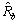 is
is
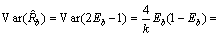
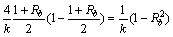 (6)
(6)
Example 2:Based on Example 1, add function b on the 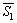 and
and 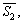 so
so 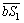 and
and 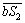 can be expressed as
can be expressed as
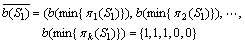
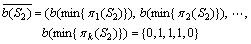
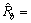
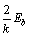 -1=
-1=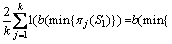
πj(S2)}))-1. With larger k, the estimated value 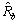 will be closer to R.
will be closer to R.
When k=1 000, the curves of 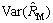 and
and 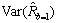 are shown in Fig. 1, and
are shown in Fig. 1, and 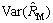 is a parabola. When R=1/2, the estimation effect of
is a parabola. When R=1/2, the estimation effect of 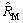 is the worst; the estimation effect of
is the worst; the estimation effect of 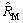 is the best with R=0 or 1 because of minimum variance.
is the best with R=0 or 1 because of minimum variance. 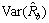 is a monotonically decreasing curve, with maximum at R=0 and minimum at R=1. With different k, the variance is also greatly changed. For detection of similarity in the case of large R, we could relax the requirement of k and reduce k.
is a monotonically decreasing curve, with maximum at R=0 and minimum at R=1. With different k, the variance is also greatly changed. For detection of similarity in the case of large R, we could relax the requirement of k and reduce k.
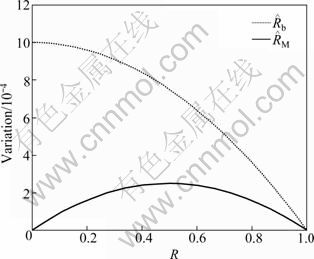
Fig. 1 Curves of R-variation relationship
Let b function be a independent random hash function to take the first one (if it is even, then 0; if it is odd, then 1). Document d could be represented as Fd=(b(min{π1(Sd)}), b(min{π2(Sd)}),…, b(min{πk(Sd)})). The corpus (size is n) could be expressed as
Mcorpus=
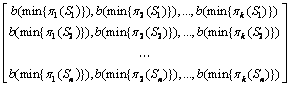 (7)
(7)
3 Hamming distance problem
In the document collection (corpus), a range query of similarity could be described as
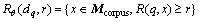 (8)
(8)
where r is the threshold similarity. Take Eq. (5) into Eq. (8), R(q, x)=2Eb-1≥r, then Eb≥(r+1)/2. The Hamming distance of fingerprint q and x is
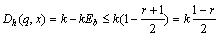 (9)
(9)
Let rh be the threshold of Hamming distance with the constraint
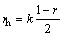 (10)
(10)
For example, when k=100, retrieve documents with R(q, x)>80%, then rh=k [(1-r)/2]=10. Therefore, given a set of k-bit fingerprint, a range query could be described as Dh(q, x)h. In Ref. [16], fingerprint grouping retrieval algorithm is proposed by Google engineers, so it is referred to as alg.G; fingerprint group merging retrieval algorithm proposed is referred to as alg.H.
3.1 Fingerprint grouping retrieval algorithm
Let k=64 and rh=3, in order to facilitate the discussion and concise, it is assumed that the fingerprints are stored in the Oracle database.
Step 1: Split 64 bits into 6 groups having 11, 11, 11, 11, 10 and 10 bits, respectively, as shown in Fig. 2. Grouping k=64 bit fingerprint as {A1(11), A2(11), A3(11), A4(11), A5(10), A6(10)}, the number of group is m=6. m must be larger than rh. Let c=m-rh, and establish 6 B+ tree indexes at {A1, A2, A3, A4, A5, A6} respectively, so that the elements of tree could be queried in time complexity O(log(n)). The corpus (size is n) could be expressed as
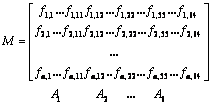
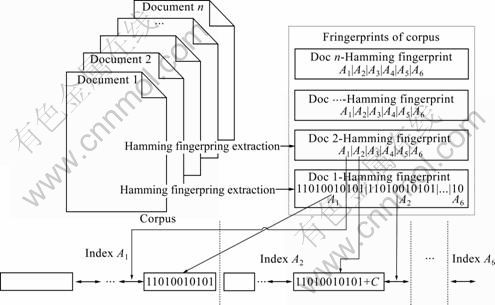
Fig. 2 Fingerprint group indexing process
Step 2: There are 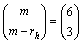 ways of choosing
ways of choosing
3 out of these 6 groups. The query document fingerprint is grouped into {Q1, Q2, Q3, Q4, Q5, Q6}. The result returned by the query condition Eq.(11) is defined as S(Pre_Query).
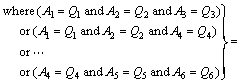
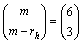 =20 (11)
=20 (11)
The time complexity of Eq. (11) is O((m-rh)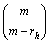 log(n)).
log(n)).
Step 3: Output the documents with {x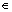 S(Pre_Query), Dh(q, x)h}. The size of S(Pre_Query) is far less than n, thus a lot of Dh calculations could be avoided.
S(Pre_Query), Dh(q, x)h}. The size of S(Pre_Query) is far less than n, thus a lot of Dh calculations could be avoided.
3.2 Limitation of alg.G
1) Alg.G is useful only in the case of high r, because the variance Eq. (6) is a monotonically decreasing function, as shown in Fig. 1. If r is very close to 1, it takes a good effect; if r reduces, the variance increases. The only option is to increase k, and the variance could be accepted within the user’s scope. If k increases, rh also increases, and then m increases. So the time complexity of alg.G significantly increases. Therefore, the application level will be very limited, only in the case of large R, such as Duplicate Web Pages Removal.
2) If r and k are fixed, rh also will be fixed, and m will be fixed. The query condition is fixed accordingly. If changing the similarity threshold r, we need to manually reset all the parameters and query condition. For example, when the similarity threshold r=0.9, k=64, and then rh=3, the query condition Eq. (9) is also fixed.
4 Fingerprint group merging retrieval algorithm
Step 1: Groups are mapped to a one-dimension shown in Fig. 3. Let C=2[k/m], each group could be mapped to [(i-1)×C, i×C) by Eq. (12):
yi=(i-1)×C+Ai (12)
{A1, A2, …, Am} is mapped to {y1, y2, …, ym}. All the groups are merged into one dimension. B + tree index named Y in the set {{y1, y2, …, ym}1, {y1, y2, …, ym}2 … {y1, y2, …, ym}n} is established. So the elements of tree could be queried in time complexity O(mlog(mn)).
Step 2: {Q1, Q2, …, Qm} is mapped to {q1, q2, …, qm}. The result returned by the query condition Eq. (13) is defined as the S(Pre_Query).
{Y=q1 union all
Y=q2 union all
…
Y=qm group by docld having count(docld) ≥m-rh} (13)
Let ng be the average size of collection under query condition {Y=qi}. Let S(group) be the set under query condition {Y=qi union all, …, Y=qm} and the size of S(group) is mng. So the time complexity of getting thez S(group) is O(mlog(mn)). The operation “Grouping by” can use HashMap. The elements of S(group) are mapped into Map. Duplicate elements will be mapped to the same key, so time complexity of “Grouping by” is O(mng). The time complexity of Eq. (13) is O(mlog(mn)+mng).
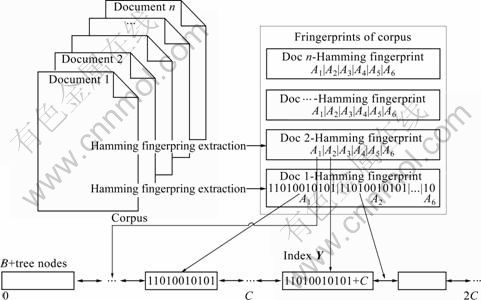
Fig. 3 Fingerprint group merging indexing process
Step 3: Output the documents with {x S(Pre_Query), Dh(q, x)h}. The size of S(Pre_Query) is far less than n, thus a lot of Dh calculations could be avoided.
S(Pre_Query), Dh(q, x)h}. The size of S(Pre_Query) is far less than n, thus a lot of Dh calculations could be avoided.
4.1 Average size of ng
If C is much smaller than n, due to the random distribution of the fingerprint, the fingerprint distribution tends to be in uniform distribution, so ng could be represented as
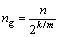 (14)
(14)
Equation (14) could be deduced by Eq. (10) and m=rh+c.
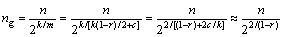 (15)
(15)
where c is a small constant. In the case of large k, 2c/k can be ignored.
4.2 Time complexity analysis of alg.G and alg.H
By combining Eq. (10), time complexity of alg.G is

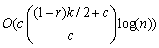 (16)
(16)
By combining Eqs. (10) and (15), time complexity of alg.H is
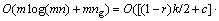
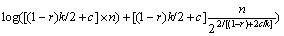 (17)
(17)
Let c=m-rh=3. If n=300 000, time complexity curves of alg.G and alg.H are shown in Fig. 4.
Figure 4 shows that the alg.H has the following advantages:
1) The similarity threshold r could be decreased in alg.H, and the range of the similarity query increases. If r decreases, then the variance increases and we must increase k to compensate the loss of variance. If k increases, rh also increases, and then m increases. So,
the time complexity of alg.G 
significantly increases. However, the time complexity of alg.H O(mlog(mn)+mng) will increase a little. Of course, alg.H must also select a high similarity threshold r, because users will not tolerate a long wait. But alg.H can be used under lower similarity threshold r and applied more widely than alg.G.

Fig. 4 Time complexity curves of alg.G (a) and alg.H (b)
2) Alg.H can increase k at any time by adding new group. The added fingerprint can be mapped to index Y. By the way, if k/m>64, Y cannot be expressed by integer index, but can be used by a string index. In the meantime, alg.H can also reduce k by deleting interval [(i-1)×C, i×C) of the data to remove a group. It is more troublesome to increase or reduce k in alg.G, and also needs to rebuild the query.
5 Experiment results and analysis
The near-duplicate detection system is designed for a research fund committee to avoid near-duplicate submissions. Approximately 300 000 experimental documents come from nearly three years of a particular fund. After minwise and b hash, the 300 000 documents can be represented as the fingerprint matrix Eq. (7), where n=300 000.
5.1 Measurement of ng
Since the argument ng has a great relationship with the time complexity of alg.H O(mlog(mn)+mng), in order to verify the time complexity analysis in Section 4.2, measuring the size of the ng has very important significance. Let k/m=8 bits be a group size. The group is mapping to Y in region [(i-1)×28, i×28), and the region size is 28=256. Choose a random number in region [(i-1)×28, i×28) to be searched in Y. The size of results (ng) is shown in Fig. 5.
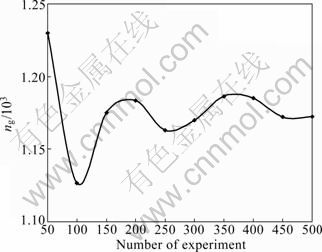
Fig. 5 Size of argument ng
Figure 5 shows that 300 000 fingerprint groups are uniformly distributed in region [(i-1)×28, i×28). Therefore, the average size of ng=n/2k/m=3000 000/28= 1 170. If continuing to increase the number of experiments, ng is infinitely close to 1 170. The experiment results confirm Eq. (14).
5.2 Precision and recall of estimation algorithm
Given a dataset Sp of document pairs, PA denotes all duplicate document pairs detected by estimation algorithm. In the PA, there is a set Pc that denotes the near-duplicate document pairs detected correctly (R>r), PE denotes near-duplicate document pairs that exist in the dataset Sp. Precision and recall are defined as
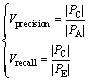 (18)
(18)
where Vprecision is the value of precision, Vrecall is the value of recall.
Figure 6 shows that when k=64, r=0.7, 0.8, 0.9, the Vprecision is 0.16, 0.19, 0.42; Vrecall is 0.74, 0.77, 0.93. When r=0.7, the Vprecision and Vrecall are both too low. So if r=0.7, k must increase to improve Vprecision and Vrecall. When k=400, Vprecision and Vrecall have a very good performance. While k=400, alg.G has ten times more time-consuming cost than alg.H.
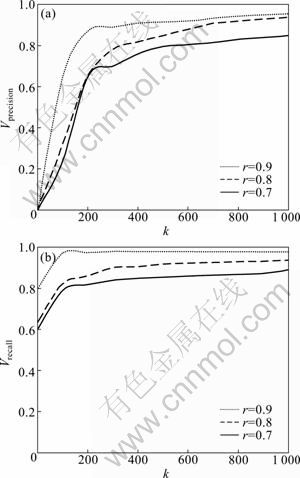
Fig. 6 Vprecision (a) and Vrecall (b) of estimation algorithm
When k=64 and r=0.9, Vrecall is 0.93, but Vprecision is 0.42. This means there are 58% of error estimations. However, because Var(r=0.9, k=64)=0.003, standard deviation is 0.05, meaning that if the estimated value is 90%, the average real value falls in region of 85.0%- 95.5%. So it can still detect high similarity of the document. And it is the reason that alg.G in Ref. [16] is also effective under small k and a high similarity threshold.
5.3 CPU time-consuming cost
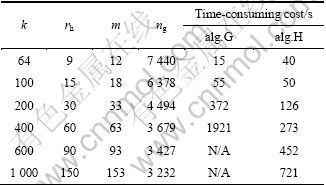
Select k=64, 100, 200, 400, 600, 1 000 in the experiments of CPU time-consuming cost. k=64 is the same environment with Ref. [16]. However, a lower similarity threshold r=0.7 is chosen. By Eqs.(10) and (14) and c=m-rh=3, the average of ng could be calculated. Selecting 1 000 random queries, the average CPU time-consuming costs of alg.G and alg.H are shown in Table 1.
When k=64 (same environment with Ref. [16]), the
time complexity of alg.G is 
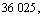 and the time complexity of alg.H is O(12log(12n)+12×7 440)=90 260. Average CPU time- consuming of alg.G is 40 s, and average retrieval time of alg.H is 15 s. It is consistent with Eqs.(16) and (17). It is noteworthy that, Var(r=0.7, k=64)=0.009 by Eq. (6), then the standard deviation is about 0.094. This means that if the estimated value is 70%, the average real value falls into the region of 60.6%-79.4%. Standard deviation is the average; there is a great chance away from the true value (70%) in the real system. So it is insufficient to estimate accurately with k=64 under r=0.7. So, it is in the need to improve k to decrease variance and improve the precision and recall under the lower similarity threshold r. When k>200, the time-consuming cost of alg.G is more than that of alg.H. When k=400, alg.G needs near 0.5 h to retrieve the similarity documents, and users can not endure such a long time. When k>600, time- consuming cost of alg.G is not available, but the time-consuming cost of alg.H can be tolerated. The experimental results comply with the time complexity analysis in Section 4.2.
and the time complexity of alg.H is O(12log(12n)+12×7 440)=90 260. Average CPU time- consuming of alg.G is 40 s, and average retrieval time of alg.H is 15 s. It is consistent with Eqs.(16) and (17). It is noteworthy that, Var(r=0.7, k=64)=0.009 by Eq. (6), then the standard deviation is about 0.094. This means that if the estimated value is 70%, the average real value falls into the region of 60.6%-79.4%. Standard deviation is the average; there is a great chance away from the true value (70%) in the real system. So it is insufficient to estimate accurately with k=64 under r=0.7. So, it is in the need to improve k to decrease variance and improve the precision and recall under the lower similarity threshold r. When k>200, the time-consuming cost of alg.G is more than that of alg.H. When k=400, alg.G needs near 0.5 h to retrieve the similarity documents, and users can not endure such a long time. When k>600, time- consuming cost of alg.G is not available, but the time-consuming cost of alg.H can be tolerated. The experimental results comply with the time complexity analysis in Section 4.2.
Table 1 CPU time-consuming costs of alg.G and alg.H (r=0.7)
6 Conclusions
1) Based on fingerprint group retrieval algorithm (alg.G), fingerprint group merging algorithm (alg.H) is proposed. The distributions of the parameter ng, time complexity and the feasibility of alg.H are analyzed.
2) It is theoretically proved that alg.H can solve the problem in alg.G: similarity threshold could not be too low and fewer fingerprints led to low accuracy. Alg.H can reduce the similarity threshold r, and increases the range of similarity queries to improve the application range. The time-consuming cost of experiments verifies the usefulness of alg.H.
3) The proposed method is easy to implement and could satisfy a wider range of similarity threshold. The similarity retrieval method has a certain reference value, and can be widely used.
References
[1] BRODER A Z, CHARIKAR M, FRIEZE A M, MITZENMACHER M. Min-wise independent permutations [J]. Journal of Computer Systems and Sciences, 2000, 60(3): 630-659.
[2] BRODER A Z. Identifying and filtering near-duplicate documents [C]// Proceeding COM ’00 Proceedings of the 11th Annual Symposium on Combinatorial Pattern Matching. London: Springer-Verlag, 2000: 1-10.
[3] BRODER A Z. On the resemblance and containment of documents [C]// Proceedings of Compression and Complexity of Sequences. Washington, DC, USA: IEEE Computer Society, 1997: 21-29.
[4] KALPAKIS K, TANG S. Collaborative data gathering in wireless sensor networks using measurement co-occurrence [J]. Computer Communications, 2008, 31(10): 1979-1992.
[5] DOURISBOURE Y, GERACI F, PELLEGRINI M. Extraction and classification of dense implicit communities in the web graph [J]. ACM Transactions on the Web (TWEB), 2009, 3(2): 1-36.
[6] BENDERSKY M, CROFT W B. Finding text reuse on the web [C]// WSDM ’09 Proceedings of the Second ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2009: 262-271.
[7] BUEHRER G., CHELLAPILLA K. A scalable pattern mining approach to web graph compression with communities [C]// WSDM ’08 Proceedings of the International Conference on Web Search and Web Data Mining. New York, USA: ACM, 2008: 95- 106.
[8] INDYK P. A small approximately min-wise independent family of hash functions [J]. Journal of Algorithm, 2001, 38(1): 84-90.
[9] CHARIKAR M S. Similarity estimation techniques from rounding algorithms [C]// STOC ’02 Proceedings of the Thirty-fourth Annual ACM Symposium on Theory of Computing. New York, USA: ACM, 2002: 380-388.
[10] LI P, K?NIG A C. b-Bit minwise hashing [C]// WWW ’10 Proceedings of the 19th International Conference on World Wide Web. New York, USA: ACM, 2010: 671-680.
[11] LI P, K?NIG A C. Theory and applications of b-Bit minwise hashing [J]. Communications of the ACM, 2011, 54(8): 101-109.
[12] LI P, MOORE J, K?NIG A C. Hashing algorithms for large-scale learning [C]// Neural Information Processing Systems (NIPS) BC. Canada: Vancouver, 2011: 35-44.
[13] BACHRACH Y, HERBRICH R. Fingerprinting ratings for collaborative filtering theoretical and empirical analysis [C]// SPIRE ’10 Proceedings of the 17th International Conference on String Processing and Information Retrieval. Berlin, Heidelberg: Springer-Verlag, 2010: 25-36.
[14] FEIGENBLAT G, PORAT E, SHIFTAN A. Exponential time improvement for min-wise based algorithms [C]// SODA ’11 Proceedings of the Twenty-Second Annual ACM-SIAM Symposium on Discrete Algorithms. USA: SIAM, 2011: 57-66.
[15] BACHRACH Y, HERBRICH R, PORAT E. Sketching Algorithms for Approximating Rank Correlations in Collaborative Filtering Systems [C]// SPIRE ’09: Proceedings of the 16th International Symposium on String Processing and Information Retrieval. London, UK: Springer-Verlag, 2009: 344-352
[16] MANKU G S, JAIN A, SARMA A D. Detecting near-duplicates for web crawling [C]// WWW ’07 Proceedings of the 16th International Conference on World Wide Web. New York, USA: ACM, 2007: 141-150.
(Edited by HE Yun-bin)
Foundation item: Project(60873081) supported by the National Natural Science Foundation of China; Project(NCET-10-0787) supported by the Program for New Century Excellent Talents in University, China; Project(11JJ1012) supported by the Natural Science Foundation of Hunan Province, China
Received date: 2012-02-10; Accepted date: 2012-05-28
Corresponding author: LONG Jun, Associate Professor, PhD; Tel: +86-18673197878; E-mail: jlong@csu.edu.cn