J. Cent. South Univ. (2018) 25: 1367-1385

DOI: https://doi.org/10.1007/s11771-018-3833-5

Numerical investigation on permeability evolution behavior of rock by an improved flow-coupling algorithm in particle flow code

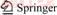
ZENG Wei(曾卫)¹, YANG Sheng-qi(杨圣奇)¹, TIAN Wen-ling(田文岭)¹, WEN Kai(文凯)²

1. State Key Laboratory for Geomechanics and Deep Underground Engineering, School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, China;

2. Laboratory of Rock Engineering and Mining Machinery, Kyushu University, Fukuoka 819-0395, Japan

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Permeability is a vital property of rock mass, which is highly affected by tectonic stress and human engineering activities. A comprehensive monitoring of pore pressure and flow rate distributions inside the rock mass is very important to elucidate the permeability evolution mechanisms, which is difficult to realize in laboratory, but easy to be achieved in numerical simulations. Therefore, the particle flow code (PFC), a discrete element method, is used to simulate permeability behaviors of rock materials in this study. Owe to the limitation of the existed solid-fluid coupling algorithm in PFC, an improved flow-coupling algorithm is presented to better reflect the preferential flow in rock fractures. The comparative analysis is conducted between original and improved algorithm when simulating rock permeability evolution during triaxial compression, showing that the improved algorithm can better describe the experimental phenomenon. Furthermore, the evolution of pore pressure and flow rate distribution during the flow process are analyzed by using the improved algorithm. It is concluded that during the steady flow process in the fractured specimen, the pore pressure and flow rate both prefer transmitting through the fractures rather than rock matrix. Based on the results, fractures are divided into the following three types: I) fractures link to both the inlet and outlet, II) fractures only link to the inlet, and III) fractures only link to the outlet. The type I fracture is always the preferential propagating path for both the pore pressure and flow rate. For type II fractures, the pore pressure increases and then becomes steady. However, the flow rate increases first and begins to decrease after the flow reaches the stop end of the fracture and finally vanishes. There is no obvious pore pressure or flow rate concentration within type III fractures.

Key words: rock mechanics; fluid-solid coupling; particle flow code (PFC); permeability; triaxial compression

Cite this article as: ZENG Wei, YANG Sheng-qi, TIAN Wen-ling, WEN Kai. Numerical investigation on permeability evolution behavior of rock by an improved flow-coupling algorithm in particle flow code [J]. Journal of Central South University, 2018, 25(6): 1367–1385. DOI: https://doi.org/10.1007/s11771-018-3833-5.

1 Introduction

Micro-to-macro cracks or fractures generate in rock mass as a result of the stress state change caused by tectonic stress or artificial activities, which weaken the strength [1], control the stress states [2] and change the permeability [3–10]. Rock permeability plays a vital role in rock engineering, such as nuclear waste disposal, unconventional gas exploration, geological sequestration and oil and gas reservoir projects [11]. It is of great significance to investigate the permeability evolution during stress state changes, and researchers have conducted many studies on permeability evolution over different hydrostatic and triaxial compression states.

In general, under hydrostatic pressure, the rock permeability decreases with increasing hydrostatic pressure. For high-permeable rock, the permeability mainly depends on the skeleton permeability rather than the pore or microcrack; hence, increasing the pressure only slightly decreases the permeability [12]. However, for low-permeable rock, compaction of the microcrack and pore can cause obvious permeability decreases [13, 14]. In rock material, the connected cracks, which are sensitive to stress, have a preferential flow path under low hydrostatic pressure, which is the major reason for the initial decrease in the permeability. Under higher hydrostatic pressure, most of the cracks are closed; hence, the pores, which are less sensitive to stress, become the main flow path, and pore compaction is the major reason for the permeability decrease. This decrease is milder than that caused by crack closure [14–16]. Permeability decreases with hydrostatic loading, and it increases during the unloading process, but the permeability cannot recover to the original state after loading [17].

Under triaxial compression tests, for the rock material with certain initial porosity or fissures, such as coal, sandstone and granite, permeability decreases under the initial deviatoric loading; with loading to a certain point, the permeability suddenly sharply increases [18–21]. In the deviatoric stress– axial strain curve, the initial concave part (closure of the microcracks) corresponds to the decreasing part of the permeability-axial strain curve; at the linear deformation stage, the permeability decreases sequentially or stays constant until the yield stage [14].

In the laboratory, due to monitoring limitations, only the apparent parameters, such as the inlet and outlet pressure and flow, can be monitored or controlled in general. However, it is hard to monitor the inner distributions of the pore pressure and flow rate, which are significant for understanding the internal mechanism of the permeability evolution. Numerical modeling allows for comprehensive monitoring, and additionally, numerical modeling is repeatable, which can compensate for the unrepeatable experiments.

PFC (Particle Flow Code), a discrete element method developed by Itasca Co. Ltd., has many advantages in damage mechanism analyses of rock mass [22–27]. THALLAK et al [28] developed a flow-coupled discrete model and applied this in an investigation of hydraulic fracturing in cohesionless granular assemblies. BRUNO [29] improved the model by adding a stress-dependent geometry and transport properties to the network elements. CUNDALL (unpublished technical note, 2000) developed a flow-coupled model based on PFC, which assumes that each particle contact is a flow channel (pipe) and these channels connect small “reservoirs” that store fluid pressure. AL-BUSAIDI et al [30] used this model to simulate hydraulically fractured Lac du Bonnet granite, and the results demonstrate that the mechanism of hydraulically induced fracture is predominantly tensile failure and that the shear cracks recorded in the hydrofracture experiment were from slips on preexisting fractures. WANG et al [31] also used the flow-couple PFC model to simulate hydrofracture, and the results of which have demonstrated adequate matching with the measured data in the field. In general, the aforementioned studies validate the applicability of flow-particle coupling in PFC.

However, for the flow-coupled model in PFC (mentioned above), the flow preference for crack over matrix is not fully embodied. Taking the simulation results from AL-BUSAIDI et al [30] (shown in Figure 1) as an example, although interconnected fractures have been driven by hydraulic injection, the pore pressure diffused evenly from the hole without any precedence to transmit through the fractures. But in real world, if fractures exist in a rock mass, the fluids tend to transit through the fractures rather than the rock matrix. In order to obtain a more realistic modeling result, in this paper, an improved flow-coupled model, which considers the preferential flow to cracks, was presented. First, based on the stress– strain and permeability–strain curves obtained from triaxial compression experiments, the mechanical micro-parameters and hydraulic micro-parameters are calibrated and validated. Compared to the original algorithm, the improved one can better simulate the percolating phenomenon. Then, the evolution of the aperture, pore pressure and flow rate distributions inside the specimen, during triaxial compression, are further studied.

Figure 1 Evolution of fluid pressures (gray circles) and propagating hydrofractures (solid lines) during hydrofracturing in homogeneous synthetic specimen with time measured in seconds [30]

2 An improved flow-coupling algorithm in PFC

PFC^2D models the movement and interaction of circular particles by the distinct element method (DEM), as described by CUNDALL et al [32]. The original application of this method was as a tool for performing research into the behavior of granular material. PFC^2D is also able to model a brittle solid, by bonding every particle to its neighbor; the resulting assembly can be considered a “solid” that has elastic properties and that is capable of “fracturing” when bonds break in a progressive manner.

In PFC^2D, the constitutive behavior of a material is simulated by associating a contact model with each contact. In addition, particles are allowed to bond together at contacts. The two standard bonding behaviors are embodied in contact bonds and parallel bonds. Both bonds can be envisioned as a type of glue joining the two particles. The contact-bond glue has a vanishingly small size that only acts at the contact point, while the parallel- bond glue has a finite size that acts over either a circular or rectangular cross-section that lies between the particles. The contact bond can only transmit a force, while the parallel bond can transmit both a force and moment. In the present study, the parallel bond model is chosen because it is considered better at simulating rock-like materials [33].

2.1 Incorporation of fluid coupling in PFC

To embody full coupling between a fluid and particles in PFC^2D, the fluid pressure and volume are associated with the voids between particles, and flow is associated with contacts according to the algorithm by CUNDALL [34]. A compacted, bonded assembly of particles is generated first. A “domain” is defined as a closed chain of particles where each link in the chain is a bonded contact (shown in Figure 2). Each link in the particle chain, named as “pipe”, connects two adjacent domains, which corresponds to a bonded contact that may break. As far as the fluid is concerned, the pipe is equivalent to a parallel-plate channel, with length (L), aperture (a) and unit depth (in the out-of-plane dimension) (shown in Figure 3). The flow rate in a pipe is given by

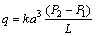                          (1)

where k is a conductivity factor, and (P₂–P₁) is the pressure difference between the two adjacent domains. The length of the pipe, L, is taken as the sum of the radii of particles adjacent to the contact in question. The aperture for a crack is usually taken to be the opening of the crack. However, to account for the matrix permeability of the uncracked material, each contact is assumed to have a “residual aperture” when it is bonded without bearing a load. Under compression, the aperture may decrease with the normal load and can be given by

                              (2)

where a₀ is the residual aperture, and F₀ is the value of normal force, F, at which the aperture decreases to a₀/2. The relationship ensures that a=a₀ for zero normal force and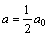for normal force equal to F₀.

When the normal force is tensile or it is zero, the aperture simply equals the sum of the residual aperture and the normal distance between the surfaces of two particles, g:

a=a₀+mg                                (3)

where m is a dimensionless multiplier for the distance scaling, which can be set different from unity for calibration purposes.

Figure 2 Domains (red dots), flow paths (black lines) and bonds (blue lines) in compacted bonded assembly of particles

As in Figure 3, each domain receives flows from the surrounding pipes: ∑q. In one timestep, △t, the increase in fluid pressure is given by the following equation, assuming that inflow is considered positive:

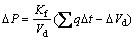                    (4)

where K_f is the fluid buik modulus and V_d is the apparent volume of the domain. The second term in the equation represents the mechanical change in the volume of the domain.

In each domain, fluid pressure may impose a force on the surrounding particles. The force vector on a typical particle is

F=Pns                                   (5)

where n is the unit normal vector of the line joining the two contact points on the particle, and s is the length of the line.

Using an explicit solution scheme, the calculation alternates between applying the flow equation to all pipes and applying the pressure equation to all domains. The critical timestep for stability is as follows. Consider a pressure perturbation, △P_p, in a single domain. The flow into the domain due to the perturbation is then calculated from Eq.(1) as

                            (6)

where R is the mean radius of the particles surrounding the domain, and N is the number of pipes connected to the domain. By Eq. (4), this flow causes a pressure response, △P_R, as follows:

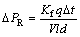                            (7)

For stability, the pressure response must be less than the original pressure perturbation; let △P_R=△P_P and the critical time can be given, from Eqs. (6) and (7), by

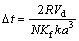                            (8)

The fluid-flow logic is implemented by applying Eqs. (1), (4) and (5) during calculation cycling.

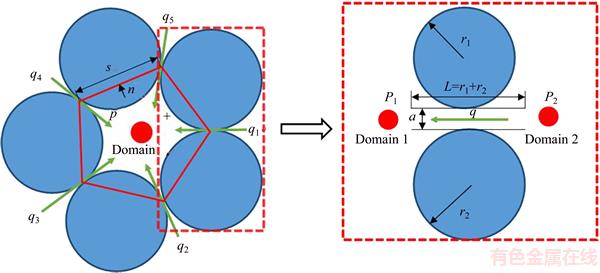
Figure 3 Sketch of fluid flow configuration

2.2 Revision of fluid coupling algorithm

As described before, a residual aperture is set to consider the matrix permeability of the uncracked material. During the loading process, the bonds on the contact may break, resulting in a crack. In the original fluid coupling algorithm, the flow channel is based on the contact bond; therefore, the corresponding channel will disappear as soon as the bond breaks. Dealing with this problem, AL-BUSAIDI et al [30] assigned the same aperture to the pipes on both bonded and broken contacts, which led to a uniform diffusion of the fluid flow that does not accord to facts. Considering a higher conductivity of cracks, HAZZARD et al [35] and ZHAO et al [36] assumed that the fluid flow through a crack is instantaneous. Therefore, when the bond between two domains fails, the fluid pressure in these domains is assumed to be their average value before the bond failure. Furthermore, ZHOU et al [37] considered the difference between the two domains and revised the equation calculating the fluid pressure. In the equivalent pore pressure method, the higher conductivity of a crack can be embodied, but the flow through a crack is no longer related to the aperture or the force exerted on the pipe. Aiming for this, we revise the fluid coupling algorithm to obtain a more realistic fluid-solid coupling system.

Figure 4 shows the flow chart of obtaining the aperture during the calculation cycling. To consider the preferential flow to cracks, the residual aperture of pipes, corresponding to the broken bonds, is set to fracture residual aperture, a_f0, which is greater than a₀. To implement this adjustment in PFC, the following steps should be added during the calculation cycle: 1) when a bond breaks, generate a crack and define a new flow channel based on two related particles and 2) judge the contact status between the two particles. If contacted, the pipe aperture can be calculated by Eq. (2) with the contact normal force and fracture residual aperture; otherwise, the pipe aperture is calculated by Eq. (3) with the fracture residual aperture and normal distance between the surfaces of the two particles.

3 Numerical model and micro-parameter calibrations

3.1 Numerical model in PFC

XU et al [19] performed a conventional triaxial compression-seepage test for sandstone specimens, which was taken from the Yuncheng coal mine at a depth of 960 m, on rock servo-controlled triaxial equipment. The cylindrical specimen has a diameter of 50 mm and length of 100 mm; there is a unit weight of 2533–2591 kg/m³.

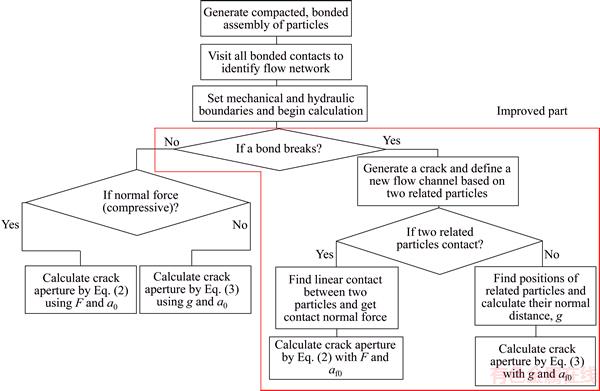
Figure 4 Flow chart of aperture calculation

On account of the requirement of great computational effort for the flow-coupling calculation, a relatively larger particle size is chosen within two-dimensional PFC (PFC^2D). As shown in Figure 5, a two-dimensional numerical specimen of 50 mm×100 mm is built, which contains 1153 particles with radius range between 2 mm and 2.5 mm.

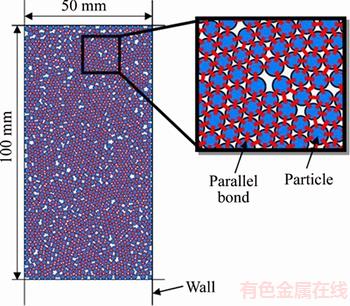
Figure 5 Numerical specimen in PFC^2D

3.2 Calibration and validation of mechanical micro-parameters

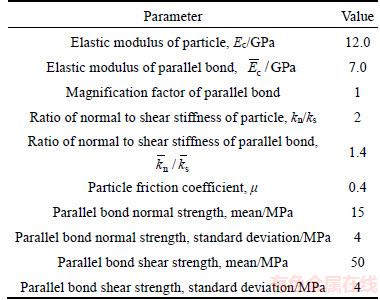
According to the testing procedure from XU et al [19], the deviatoric stress was increased stepwise after the confining pressure application, up to each selected deviatoric stress level. Both the axial and radial stresses were maintained at constant levels; then, the transient flow procedure was performed to measure the permeability. After the measurement, the specimen was loaded to the next deviatoric stress levels until ultimate failure. To match with the obtained stress–strain curves, the trial and error method, suggested by the PFC manual [38], is used to calibrate the micro- parameters, and a group of micro-parameters, listed in Table 1, is obtained.

To validate the micro-parameters, the numerical results of the triaxial compression tests are compared with the experimental ones.Figures 6(a)–(c) show the comparison of the axial and radial strain–deviatoric stress curves under 5, 15 and 25 MPa confining pressure,respectively. Obviously, under each confining pressure, the numerical curves are in good agreement with experimental ones. Notice that the experimental curves show a slightly hackly shape before peak stress, which mainly results from the permeability measurement. Figure 6(d) shows the peak stress variation with confining pressure. The peak strength increases linearly with the confining pressure, which can be well depicted by Mohr-Coulomb criterion.

Table 1 Mechanical micro-parameters of PFC^2D

The ultimate failure modes of numerical and experimental specimens are compared in Figure 7. The failure modes of the numerical specimens are very similar to that of the experimental specimens. Under 5 MPa confining pressure, a mix of shear and tensile failure occurs, and the shear failure dominates as the confining pressure increases to 15 and 25 MPa.

From the comparison of the stress–strain curves and failure mode between numerical and experimental results, it is fully certified that the chosen mechanical micro-parameters are suitable for modeling the targeted sandstone used by XU et al [19].

4 Steady flow test and hydraulic micro- parameter calibration

In the experiment [19], the permeability was measured at each pre-designed deviatoric stress level using the transient-pulse method. In addition, the steady flow test is also a widely used permeability measurement method. In this method, constant inlet and outlet pressures with a certain pressure difference are exerted on both ends of the tested specimen; then, the outlet flow rate is measured. When the flow rate reaches a steady state, the specimen permeability can be calculated.

The steady flow test is not preferred for low- permeability material in laboratory experiments, because it takes long measuring time and it is difficult to monitor with high precision [39]. However, these problems can be settled in the numerical simulation, and for it is intuitional and concise to obtain the permeability, the steady flow method is chosen for the permeability measurement in the numerical simulation.

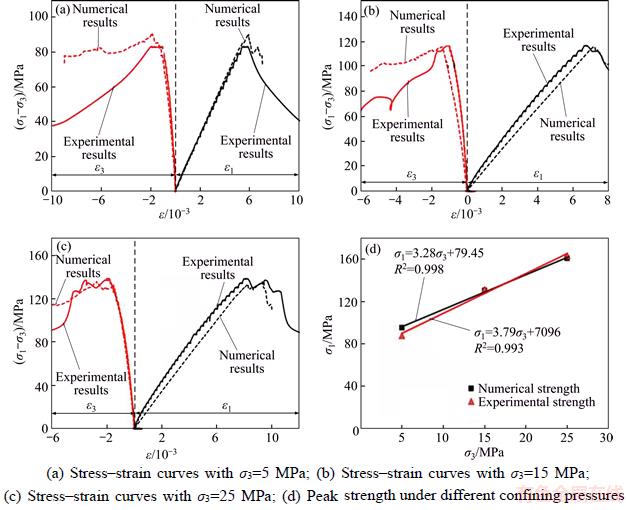
Figure 6 Comparison between experimental [19] and numerical results of triaxial compression tests:

Figure 7 Comparison of triaxial compression failure mode between experiment and simulation:

4.1 Build steady flow test model and hydraulic micro-parameters

Figure 8 depicts the steady flow test model in PFC^2D. Constant inlet pressure, P_in, and outlet pressure, P_out, have been imposed on the top and bottom 5 mm range of the tested specimen. In the middle of the specimen, a pressure measure box of 10 mm height and horizontal flow rate measure line are set. The average pore pressure inside the pressure measure box is recorded as P_m and the total flow rate through the flow rate measure line is recorded as q_m (from inlet to outlet is positive). P_m and q_m of each timestep are monitored, and the flow steady status is reached while both remain constant. According to the Darcy law, the specimen permeability K can be given by

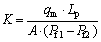                         (9)

where L_p equals the specimen height minus the inlet and outlet region height, which is the flow path length; also, A is the cross sectional area of the specimen, which equals specimen width multiplied by the unit length in two dimensions.

To minish the impact of fluid pressure, the inlet and outlet pressures are set to far less than the confining pressure as P_in=0.1 MPa and P_out=0 MPa. Based on the permeability–strain curve obtained from the triaxial compression test under 5 MPa confining pressure [19], the hydraulic micro- parameters are calibrated using the trial and error method. The obtained group of the parameters is listed in Table 2.

Figure 8 Model for steady-state method in PFC^2D

Table 2 Hydraulic micro-parameters in PFC^2D

4.2 Hydraulic micro-parameter validation and improved algorithm validation

To validate the improved algorithm and hydraulic micro-parameters, the permeability evolution under triaxial compression of simulation is compared with the experimental results (of specimen I1^# from literature [19]) in Figure 9. In this figure, the permeability from the experiment and simulation of the original and improved algorithm are denoted as K_E, K_SO and K_SR, respectively. Notice that the experimental permeability data from literature [19] are denoted in unit m². For better comparing with the numerical results, the experimental data have been multiplied by unit weight (γ) and divided by dynamic viscosity (μ) of the fluid, and therefore transformed to permeability denoted in unit m/s, which is the same to the numerical results.

As seen from the experimental curve in Figure 9, the permeability–strain curve can be divided into two stages, the initial region is the pore flow stage which is followed by the fracture flow stage. In the pore flow stage, permeability decreases slowly with increasing deviatoric stress, which mainly results from the closure of existing microcracks and compaction of pores. As loading proceeds, the permeability suddenly increases sharply at a certain point, which is called the percolation effect, and the corresponding axial stress is termed the percolation strength [40]. From this point, fractures grow, and the specimen transitions from pore flow to fracture flow.

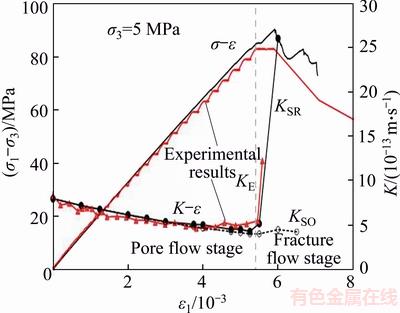
Figure 9 Comparison of experimental and numerical results of permeability evolution during triaxial compression under 5 MPa confining pressure (Red: experimental results [19], black: numerical results. K_E denotes the experimental permeability; K_SR denotes the numerical permeability from improved algorithm; K_SO denotes the numerical permeability from original algorithm)

As shown in Figure 9, at the pore flow stage, the simulated permeability from both the original and improved algorithm are in agreement with the experimental one. However, the permeability from the original algorithm does not show an obvious uprush at the percolation point while the results from improved algorithm perfectly show the percolation phenomenon. Which fully demonstrates that the improved algorithm is more reasonable.

As shown in Table 2, the fracture residual aperture, a_f0, is taken as 10 times the matrix residual aperture, a₀. On the basis of Darcy’s law, the fracture-matrix permeability ratio, k_f/k_m, is cubic of the aperture ratio, a_f0/a₀, which leads to k_f/k_m equaling to approximately 10³. MATTH et al [41], according to field data, discovered the following 3 regimes of fluid flow partitioning between fractures and rock matrix: 1) when the fracture-matrix permeability ratio, k_f/k_m, is less than 10², fractures do not perturb flow and have a negligible effect on effective permeability; 2) when k_f/k_m is in the range of 10³–10⁴, fractures strongly perturb flow and carry as much of it as the rock matrix; and 3) when k_f/k_m is greater than 10⁵–10⁶, fractures carry all of the flow while the matrix is stagnant. In the present study, the k_f/k_m is approximately 10³, which indicates that the fracture carries significant flow levels.

It is worth noting that the percolation strength usually corresponds to the stress at which the volumetric strain transfers from the compaction to dilation [20, 40, 42, 43]. The stress evolution against the axial, radial and volumetric strains and the permeability evolution against axial strain are shown in Figure 10(a) for experimental results and Figure 10(b) for numerical results of the improved algorithm. In both the experimental and numerical results, the stress level at the turning point from compaction to dilation agrees with the percolation strength, which occurs when the permeability curve suddenly increases sharply. The results strongly support the discoveries of other researchers. Moreover, the results validate that the mechanism of permeability uprush is in agreement with the actual mechanism.

4.3 Further validation of hydraulic micro- parameters

In nature, the distribution of the microcracks and pores of the same rock material or even the same rock block differs from place to place. In Figure 11(a), the stress–strain curve and permeability–strain curve of specimen I3^# and J3^# (from Ref. [19]), taken from the same rock at the same place, are compared. It can be observed that, the stress curves of each specimen are close, while the permeability curves differ greatly from each other. This is because the permeability is very sensitive to the microcrack and pore distribution compared to the mechanical properties.Figure 11(b) shows the comparison of the dimensionless permeability–strain curves of specimens I3^# and J3^#, and the evolution of dimensionless permeability of the specimens is in accordance. Therefore, we can choose the permeability ratio K/K₀ for the comparison between different specimens that are taken from the same rock material under different stress conditions.

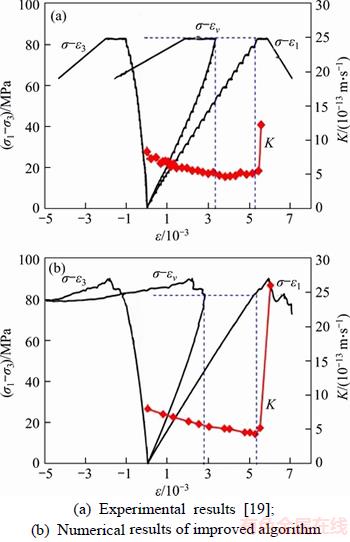
Figure 10 Stress–strain curves and permeability–strain curves of triaxial compression under 5 MPa confining pressure:

For a further validation, permeability-strain curves from experiments and numerical simulations are compared in Figures 12(a) (σ₃=15 MPa) and (b) (σ₃=25 MPa). The hydraulic parameters are calibrated based on specimen I1^# (σ₃=5 MPa), which differs from the specimens used for tests under 15 and 25 MPa confining pressures. Therefore, the permeability ratio K₀, should be used. Based on Figure 12, K_E, K_SO and K_SR decrease with increasing load at the pore flow stage, due to the pore compaction; then K_E and K_SR increase sharply at a certain point, due to the fracture growth, while K_SO slightly increases.

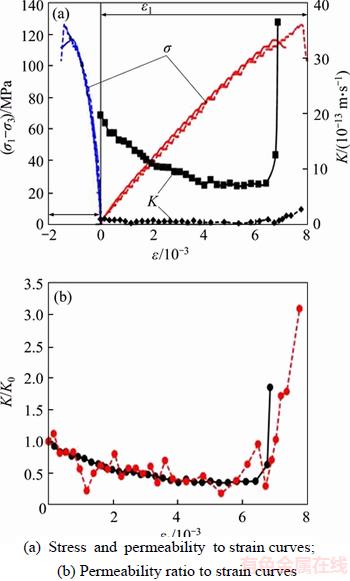
Figure 11 Experimental results of permeability test under confining stress 15 MPa with different permeation differentials [19] (Solid line: △P=0.3 MPa, J₃^#; Dashed line: △P=0.2 MPa, I₃^#):

However, strictly speaking, the complete triaxial compression-permeability tests are unrepeatable in the laboratory. Nevertheless, the numerical simulation is capable of building exactly the same specimens; as a result, it is used for the repetitive permeability analysis in the study.

The permeability and volumetric strain evolutions during triaxial compression are shown in Figure 13. In Figure 13(b), at the initial loading part, the permeability decreases with increasing stress and then surges up at the percolation threshold for all three curves. In addition, comparing Figures 13(a) and (b), the percolation threshold also corresponds to the turning point for volumetric strain transfer from compaction to dilation.

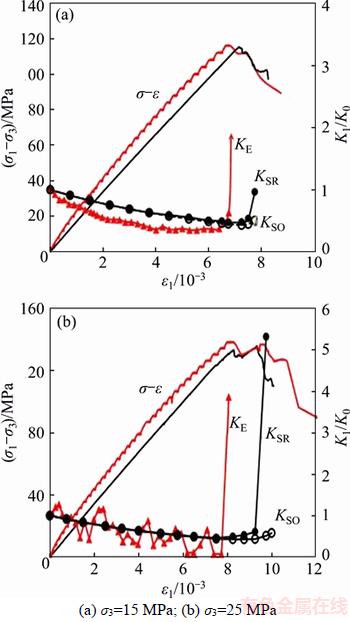
Figure 12 Comparison of experimental and numerical results of permeability evolution during triaxial compression (Red: experimental results [19]; black: numerical results. K_E is the experimental permeability; K_SR is the numerical permeability from improved algorithm; K_SO is the numerical permeability from original algorithm):

Shown in Figure 13(b), at the pore flow stage (before the percolation threshold), the permeability decreases with the confining pressure. It mainly results from the pore compaction caused by higher confining pressure, and the pores are the main flow path in this stage. At the pore flow stage, the permeability–stress curves, under 5, 15 and 25 MPa confining pressures, can be well described by linear fitting, and the R² are 0.982, 0.977 and 0.981, respectively. Under 5 MPa confining pressure, the slope of the fitting line is 0.042, which decreases to 0.024 and 0.016 under 15 and 25 MPa confining pressures, respectively. The pores are more compacted under high pressure, which makes them harder to be further compacted; therefore, the permeability decreases faster at low confining pressure and slower at high confining pressure. Observed from Figure 13(c), under 5 and 25 MPa confining pressure, the percolation strength is slightly lower than the peak strength, which explains why interconnected fractures are formed and fracture flow is initiated before reaching the peak strength. However, for 15 MPa confining pressure, the percolation is almost equal to the peak strength at which the interconnected fractures formed.

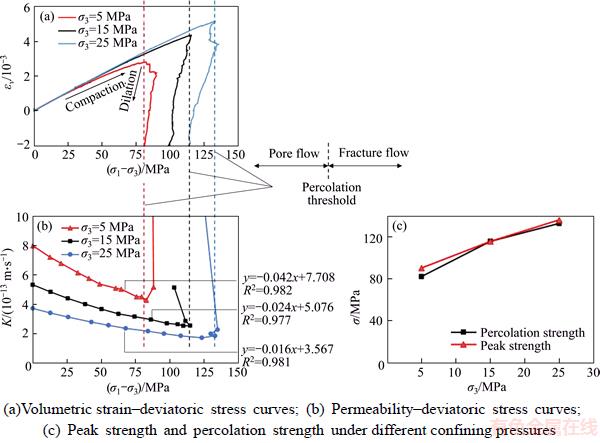
Figure 13 Triaxial compression flow test numerical results under different confining pressure:

5 Steady flow process

5.1 Effects of confining pressure and deviatoric stress on flow process

As described in Section 4.1, a pressure measure box and flow rate measure line are set at the middle of the numerical rock specimen to measure the fluid pressure P_M and flow rate q_M. In Figures 14(a) and (b), the evolution of P_M and q_M during the flow process, under hydrostatic pressure of 5, 15 and 25 MPa, are depicted. As shown in Figure 14(a), the pore pressure in the middle of the specimen first increases and then remains steady. The increasing rate decreases with increasing hydrostatic pressure; therefore, the lower the pressure, the sooner the steady state will be reached. Apparently, the pore pressure, P_M, stays steady at nearly 0.05 MPa, which is the average value of the inlet and outlet pressures, under each hydrostatic pressure level. Because under the hydrostatic state, no macro crack emits inside the specimen, and there is a uniform gradient distribution in the pore pressure after steady state is reached. As shown in Figure 14(b), as the pore pressure evolves, the flow rate q_M first increases and then reaches a steady state. Under lower hydrostatic pressure, the increasing rate flow q_M is faster and it takes less time to reach the steady. Unlike the pore pressure, the flow rate does not remain steady at the same value, but remains steady at the higher value under the lower hydrostatic pressure. The flow rate shows a uniform distribution at the steady state for the uncracked specimen.

The pore pressure and flow rate at the middle of the specimens, P_M and q_M, which change with deviatoric stress, are depicted in Figures 14(c) and (d) (σ₃=5 MPa). Notice that the selected deviatoric stress levels are before the percolation threshold; therefore, no interconnected fractures are formed and the specimen is still at the pore flow stage. It is clear that, during the pore flow stage, pore pressure and flow rate evolutions with deviatoric stress are very similar to the evolutions with hydrostatic pressures, except the impaction of the hydrostatic pressure is stronger than the deviatoric stress.

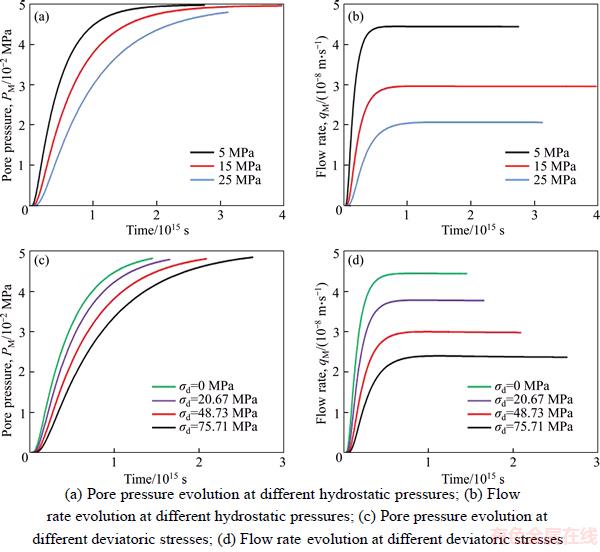
Figure 14 Evolution of pore pressure and flow rate at middle part of specimen under different hydrostatic pressures and different deviatoric stresses (at pore flow stage):

5.2 Flow process of intact specimen

The specimen under 5 MPa hydrostatic pressure is selected as an example for analyzing the flow process of the intact specimen. In Figure 15, the pore pressure and flow rate distributions that evolve with time are depicted. At the initial point A, the pore pressure at the inlet region is kept at 0.1 MPa, and it only migrates downward a little. There is no pressure gradient in the inlet region, therefore, almost no fluid flow occurs inside the inlet region. But, at the bottom of the inlet region, the existing pressure gradient drives fluid flow downwards. When the flow process reaches point C, the fluid reaches the specimen bottom, and the pore pressure and flow rate are both distributed in a gradient. As the specimen reaches its steady state at point D, the pore pressure shows a uniform gradient distribution while the flow rate shows a uniform distribution.

5.3 Flow process of fractured specimen

Cracks and fractures inside the rock specimen affect the fluid flow, and the triaxial compression under different confining pressures leads to different failure modes, which results in different flow situations. After the triaxial compression failure, when the axial stress decreases to 80% of its peak strength, a certain aperture distribution forms inside the rock specimen. Without considering the water coupling, the flow aperture distributions obtained from improved algorithm (RA) and original algorithm (OA) are compared in Figure 16. The flow aperture distribution from the RA is more concentrated on the fractures compared to the OA for each confining pressure. Furthermore, the flow aperture is more concentrated under 5 MPa confining pressure comparing to that under the 25 MPa confining pressure, which mainly results from the restraining effect of the higher confining pressure.

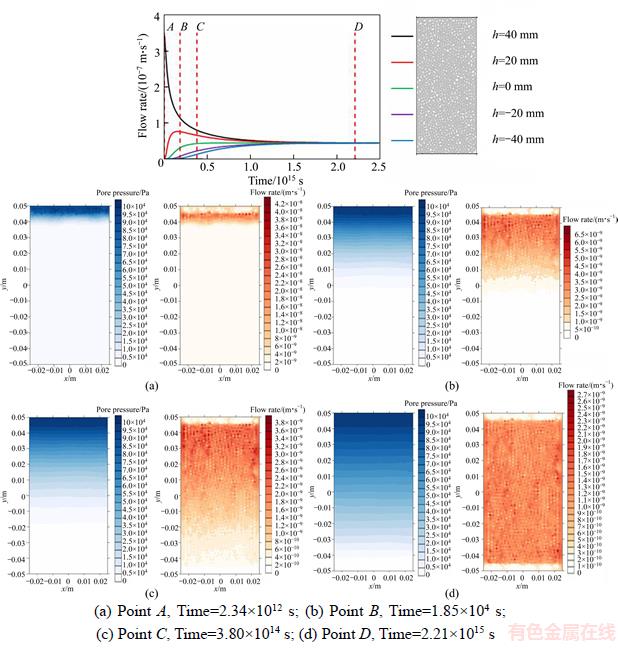
Figure 15 Pore pressure and flow rate distributions evolving with time under 5 MPa hydrostatic pressure (Pore pressure is denoted as blue while flow rate is denoted as red):

In this study, the flow processes of the fractured specimens, from triaxial compression under 5 MPa (shown in Figure 17) and 25 MPa (shown in Figure 18) confining pressure, are taken as examples for the flow analysis. As observed in Figure 17, at the beginning, point A, of the flow process, the pore pressure and flow rate both quickly and preferentially transmit through existed fractures, while they are mildly spread to the intact matrix. Three major flow paths, F₁, F₂ and F₃, have formed in the fractures linking to the inlet region. The major flow path may divide into several branches. As the flow process reaches point B, pore pressure is transmitted through the major flow paths. Flow path F₁ is still extending to the bottom, while F₂ and F₃ stopped at approximately 30–40 mm apart from the specimen top. As the fluid reaches the stop end of the flow path, the flow rate decreases and even vanishes. Therefore, the flow rates in F₂ and F₃ are much lower than in F₁. When the flow process reaches point C, the pore pressure and flow rate still transmit to the outlet through F₁, while an obvious flow rate has vanished in F₂ and F₃. As the flow process reaches at point D, the pore pressure traverses into matrix around the fractures, while the obvious flow rate only goes through the flow path connecting the inlet and outlet. From the flow rate distribution, we can see that the flow rate is much higher when it goes through the narrow flow path. It is worth noting that the flow rate generally increases when the crack number slightly increases due to the flow active.

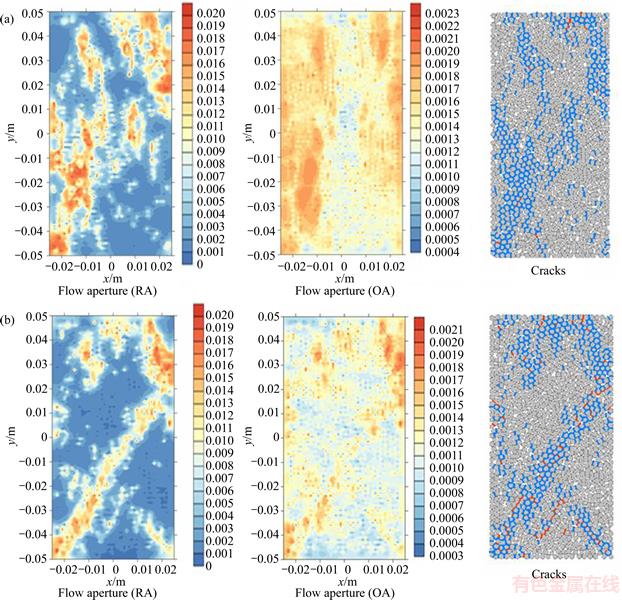
Figure 16 Flow aperture, pore pressure, flow rate and crack distributions of failed specimen under 5 MPa (a) and 25 MPa (b) confining pressure (RA represents the improved algorithm, OA represents the original algorithm)

The pore pressure and flow rate evolution of the specimen failed at triaxial compression (σ₃=25 MPa) are depicted in Figure 18. Just as the flow process of the specimen failed at a 5 MPa confining pressure, the pore pressure and flow rate both prefer to transmit through the fractures than the rock matrix. The fractures can be divided into the following three types: I) fractures link to both the inlet and outlet, II) fractures link to the inlet but the outlet, and III) fractures that do not link to the inlet. In the type II fracture, pore pressure increases and finally stayed steady, but the flow rate increases first; it then decreases after the flow reaches the stop end of the fracture and finally vanishes. There is no obvious pore pressure or flow rate concentration on the type III fractures. Finally, the flow rate only concentrates on the type I fractures. Due to the different failure modes caused by different confining pressures, the final flow path of the failed specimen at a 5 MPa confining pressure is a tensile fracture, which is in parallel with the axial loading direction, while the one at a 25 MPa confining pressure is an inclined shear fracture.

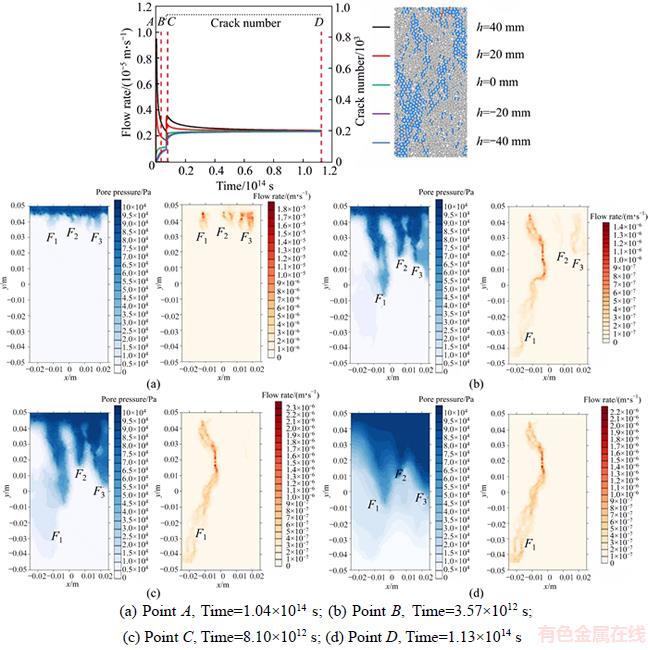
Figure 17 Pore pressure and flow rate distributions evolving with time after triaxial compression failure under σ₃=5 MPa (Pore pressure is denoted as blue while flow rate denoted as red):

6 Conclusions

1) An improved solid-fluid coupling algorithm considering the preferential flow in fracture was proposed. Comparing to the original solid-fluid coupling algorithm, the improved algorithm demonstrates better simulating of the percolation effect.

2) The permeability–strain curve during the triaxial compression test can be divided into two stages, the pore flow and fracture flow stage. At the pore flow stage, permeability decreases with increased loading. It results from the compaction of the pores, which are the main flow channels. The boundary of the two stages is the percolation threshold, at which, permeability encounters a sharp increasing and the volumetric strain transfer from the compaction to the dilation. The specimen enters into the fracture flow stage after the percolation threshold.

3) Under the hydrostatic states and deviation stress states, the P_M and q_M both go through an increasing at first and then reach a steady value during the steady flow process. The steady value of q_M decreases with the hydrostatic pressure or deviatoric stress, while the steady value of P_M is always 0.05 MPa, which is the average value of the inlet and outlet pressures. When the intact specimen reaches the steady state, the pore pressure shows an average gradient distribution and the flow rate shows a uniform distribution.

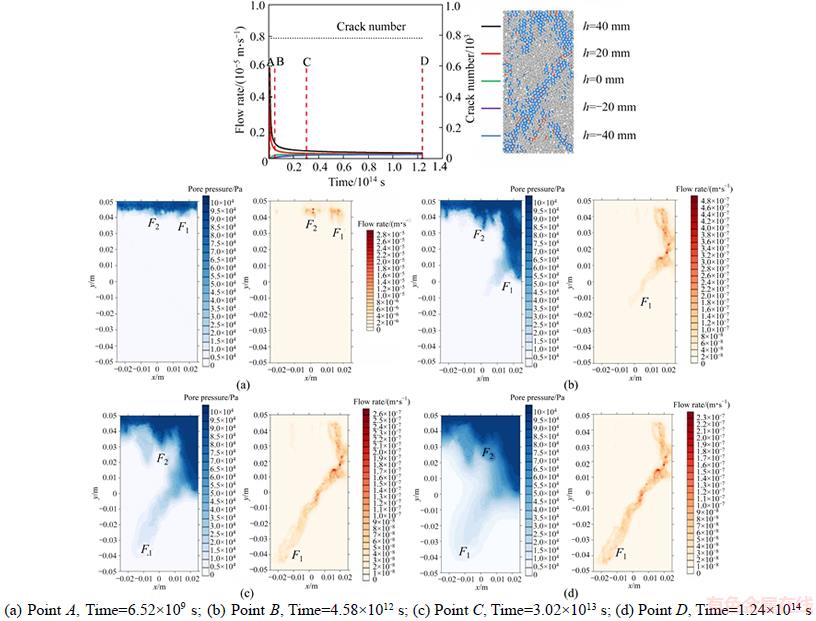
Figure 18 Pore pressure and flow rate distributions evolve with time after triaxial compression failure under σ₃=25 MPa (Pore pressure is denoted as blue while flow rate denoted as red):

4) After the triaxial compression failure, a certain aperture distribution forms inside the rock specimen. The flow aperture distribution from the improved algorithm is more concentrated on the fractures compared to that from the original algorithm for each confining pressure. When the confining pressure is 5 MPa, the flow aperture is more concentrated comparing to that at a 25 MPa confining pressure, which mainly results from the restraining effect of the higher confining pressure.

5) During the steady flow process, pore pressure and flow rate both prefer transmitting through the fractures rather than the rock matrix. The fractures can be divided into the following three types: I) fractures link to both the inlet and outlet, II) fractures link to the inlet but the outlet, and III) fractures do not link to the inlet. Type I fracture is always the preferential propagating path for both the pore pressure and flow rate. In type II fracture, the pore pressure increases and remains steady finally, however, the flow rate increases first and decreases after the flow reaches the stop end of the fracture, which finally vanishes. There is no obvious pore pressure and flow rate concentration on type III fractures.

Nomenclature:

k

Micro conductivity factor (m/s)

L

Length of the flow pipe (m)

r_i

Radius of the particle i (i=1, 2) (m)

P₁

Pressure of domain i (i=1, 2) (Pa)

a₀

Matrix residual aperture (m)

a_0f

Fracture residual aperture (m)

F₀

Half-aperture normal force (Pa)

m

Dimensionless multiplier for the distance scaling

g

Normal distance between the surfaces of the two particles (m)

∑q

flows domain receiving from the surrounding pipes (m³)

△t

Timestep (s)

K_f

Fluid bulk modulus (Pa)

V_d

Apparent volume of the domain (m³)

F

Force that fluid pressure is imposing on surrounding particles (N)

s

Length of the line joining the two contact points on the particle (m)

△P_p

Pressure perturbation (Pa)

△P_R

Pressure response (Pa)

σ₃

Confining pressure (MPa)

σ₁

Major principle stress (MPa)

ε₁

Axial strain (10^–3)

ε₃

Lateral strain (10^–3)

ε_v

Volumetric strain (10^–3)

K

Sample permeability (m/s)

L_p

Flow path length (m)

A

Cross sectional area (m²)

P_in

Inlet pressure (Pa)

P_out

Outlet pressure (Pa)

P_M

Average pore pressure in the pressure measure box (Pa)

q_m

Total flow rate go through the flow rate measure line (m/s)

E_c

Elastic modulus of particle (Pa)

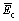
Elastic modulus of parallel bond (Pa)

k_n

Normal stiffness of particle (N/m)

k _s

Shear stiffness of particle (N/m)

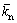
Normal stiffness of parallel bond (N/m)

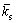
Shear stiffness of parallel bond (N/m)

μ

Particle friction coefficient

References

[1] HOEK E, BROWN E T. Empirical strength criterion for rock masses [J]. Journal of the Geotechnical Engineering Division, 1980, 106(9): 1013–1035. DOI: https://doi.org/10.1016/ 0148- 9062(81)90766-X.

[2] TOWNEND J, ZOBACK M D. How faulting keeps the crust strong [J]. Geology, 2000, 28(5): 399–402. DOI: https:// doi.org/10.1130/0091-7613(2000)28<399:hfktcs>2.0.co;2.

[3] KNIPE R J. Faulting processes and fault seal [J]. Structural & Tectonic Modelling & Its Application to Petroleum Geology, 1992: 325–342. DOI: https://doi.org/10.1016/ B978-0- 444-88607-1.50027-9.

[4] SHIPTON Z K, EVANS J P, ROBESON K R, FORSTER C B, SNELGROVE S H. Structural heterogeneity and permeability in faulted eolian sandstone: Implications for subsurface modeling of faults [J]. AAPG Bulletin, 2002, 86(5): 863–883. DOI: https://doi.org/10.1306/61EEDBC0-173E- 11D7-8645000102C1865D.

[5] BRACE W F. Permeability of crystalline and argillaceous rocks [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1980, 17(5): 241–251. DOI: https://doi.org/10.1016/0148-9062(80)90807- 4.

[6] ANTONELLINI M A, AYDIN A. Effect of faulting on fluid flow in porous sandstones: Petrophysical properties [J]. AAPG Bulletin, 1994, 78(3): 355–377. DOI: https://doi.org/ 10.1306/8D2B1B60-171E-11D7-8645000102C1865D.

[7] BARTON C A, ZOBACK M D, MOOS D. Fluid flow along potentially active faults in crystalline rock [J]. Geology, 1995, 23(8): 683. DOI: https://doi.org/10.1130/0091- 7613(1995)023<0683:FFAPAF>2.3.co;2.

[8] HEAP M J, KENNEDY B M. Exploring the scale-dependent permeability of fractured andesite [J]. Earth & Planetary Science Letters, 2016, 447: 139–150. DOI: https://doi.org/ 10.1016/j.epsl.2016.05.004.

[9] RAWLING G C, GOODWIN L B, WILSON J L. Internal architecture, permeability structure, and hydrologic significance of contrasting fault-zone types [J]. Geology, 2001, 29(1): 43–46. DOI: https://doi.org/10.1130/0091- 7613(2001)029<0043:IAPSAH>2.0.co;2.

[10] SAUL CAINE J, EVANS J P, FORSTER C B. Fault zone architecture and permeability structure [J]. Geology, 1996, 24(11): 1025–1028. DOI: https://doi.org/10.1130/0091- 10.1130/0091-7613(1996)024<1025:FZAAPS>2.3.co;2.

[11] JIA C J, XU W Y, WANG H L, WANG R B, JUN Y U, YAN L. Stress dependent permeability and porosity of low-permeability rock [J]. Journal of Central South University, 2017, 24(10): 2396–2405. DOI: https://doi.org/ 10.1007/s11771-017-3651- 1.

[12] BRACE W F. A note on permeability changes in geologic material due to stress [J]. Pure and Applied Geophysics, 1978, 116(4): 627–633. DOI: https://doi.org/10.1007/ BF00876529.

[13] MORROW C A, LOCKNER D A. Permeability and porosity of the Illinois UPH 3 drillhole granite and a comparison with other deep drillhole rocks [J]. Journal of Geophysical Research Atmospheres, 1997, 102(B2): 3067–3075. DOI: https://doi.org/10.1029/96JB03178.

[14] ZHU W, WONG T F. The transition from brittle faulting to cataclastic flow: Permeability evolution [J]. Journal of Geophysical Research Solid Earth, 1997, 102(B2): 3027– 3042. DOI: https://doi.org/10.1029/96JB03282.

[15] SURI P, AZEEMUDDIN M, ZAMAN M, KUKRETI A R, ROEGIERS J C. Stress-dependent permeability measurement using the oscillating pulse technique [J]. Journal of Petroleum Science & Engineering, 1997, 17(3, 4): 247–264. DOI: https://doi.org/10.1016/S0920- 4105(96)00073-3.

[16] DAVID C, MENENDEZ B, ZHU W, DAVID C, MENENDEZ B, ZHU W, WONG T F. Mechanical compaction, microstructures and permeability evolution in sandstones * [J]. Physics & Chemistry of the Earth Part A: Solid Earth & Geodesy, 2001, 26(1, 2): 45–51. DOI: https://doi.org/10.1016/S1464-1895(01)00021-7.

[17] LIU Z B, SHAO J F, HU D W, XIE S Y. Gas permeability evolution with deformation and cracking process in a white marble under compression [J]. Transport in Porous Media, 2016, 111(2): 1–15. DOI:10.1007/s11242-015-0603-9.

[18] ZENG K, XU J, HE P, WANG C G. Experimental study on permeability of coal sample subjected to triaxial stresses [J]. Procedia Engineering, 2011, 26(1): 1051–1057. DOI: https://doi.org/10.1016/j.proeng.2011.11.2273.

[19] XU P, YANG S Q. Permeability evolution of sandstone under short-term and long-term triaxial compression [J]. International Journal of Rock Mechanics & Mining Sciences, 2016, 85: 152–164. DOI: https://doi.org/10.1016/j.ijrmms. 2016. 03.016.

[20] MITCHELL T M, FAULKNER D R. Experimental measurements of permeability evolution during triaxial compression of initially intact crystalline rocks and implications for fluid flow in fault zones [J]. Journal of Geophysical Research-Solid Earth, 2008, 113(B11): 226–227. DOI: https://doi.org/10.1029/2008JB005588.

[21] WANG H, XU W, SHAO J, SKOCZYLAS F. The gas permeability properties of low-permeability rock in the process of triaxial compression test [J]. Materials Letters, 2014, 116(2): 386–388. DOI: https://doi.org/10.1016/j.matlet.2013.11.061.

[22] CHENG C, CHEN X, ZHANG S. Multi-peak deformation behavior of jointed rock mass under uniaxial compression: Insight from particle flow modeling [J]. Engineering Geology, 2016, 213: 25–45. DOI: https://doi.org/10.1016/ j.enggeo.2016.08.010.

[23] FAN X, KULATILAKE P H S W, CHEN X. Mechanical behavior of rock-like jointed blocks with multi-non- persistent joints under uniaxial loading: A particle mechanics approach [J]. Engineering Geology, 2015, 190: 17–32. DOI: https://doi.org/10.1016/j.enggeo.2015.02.008.

[24] YANG S Q, HUANG Y H, JING H W, LIU X R. Discrete element modeling on fracture coalescence behavior of red sandstone containing two unparallel fissures under uniaxial compression [J]. Engineering Geology, 2014, 178(6): 28–48. DOI: https://doi.org/10.1016/j.enggeo.2014.06.005.

[25] YANG X X, KULATILAKE P H S W, CHEN X, JING H W, YANG S Q. Particle flow modeling of rock blocks with nonpersistent open joints under uniaxial compression [J]. International Journal of Geomechanics, 2016, 16(6): 04016020. DOI: https://doi.org/10.1061/(ASCE)GM.1943- 5622.0000649.

[26] HUANG Y H, YANG S Q, ZENG W. Experimental and numerical study on loading rate effects of rock-like material specimens containing two unparallel fissures [J]. Journal of Central South University, 2016, 23(6): 1474–1485. DOI: https://doi.org/10.1007/s11771-016-3200-3.

[27] YANG X X, JING H W, CHEN K F, YANG S Q. Failure behavior around a circular opening in a rock mass with non-persistent joints: A parallel-bond stress corrosion approach [J]. Journal of Central South University, 2017, 24(10): 2406–2420. DOI: https://doi.org/10.1007/s11771- 017-3652-0.

[28] THALLAK S, ROTHENBURG L, DUSSEAULT M. Simulation of multiple hydraulic fractures in a discrete element system [C]// Proceedings of the The 32nd US Symposium on Rock Mechanics. Norman, Oklahoma, F, 1991.

[29] BRUNO M S. Micromechanics of stress-induced permeability anisotropy and damage in sedimentary rock [J]. Mechanics of Materials, 1994, 18(1): 31–48. DOI: https://doi.org/ 10.1016/0167-6636(94)90004-3.

[30] AL-BUSAIDI A, HAZZARD J F, YOUNG R P. Distinct element modeling of hydraulically fractured Lac du Bonnet granite [J]. Journal of Geophysical Research Solid Earth, 2005, 110(B6): 351–352. DOI: https://doi.org/10.1029/ 2004JB003297.

[31] WANG T, ZHOU W, CHEN J, XIAO X, LI Y, ZHAO X Y. Simulation of hydraulic fracturing using particle flow method and application in a coal mine [J]. International Journal of Coal Geology, 2014, 121: 1–13. DOI: https://doi.org/10.1016/j.coal.2013.10.012.

[32] CUNDALL P A, STRACK O D L. A discrete numerical mode for granular assemblies [J]. Géotechnique, 1979, 29(1): 47–65. DOI: https://doi.org/10.1680/geot.1979.29.1.47.

[33] CHO N, MARTIN C D, SEGO D C. A clumped particle model for rock [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(7): 997–1010. DOI: https://doi.org/ 10.1016/j.ijrmms.2007.02.002.

[34] CUNDALL P A. Fluid Formulation for PFC^2D [M]. Minneapolis, MN, USA: Itasca Consulting Group, 2000.

[35] HAZZARD J F, YOUNG R P, OATES S J. Numerical modelling of seismicity induced by fracture injections in a fractured reservoir [C]// Proceedings of the In Proceedings of the 5th North American Rock Mechanics Symposium Mining and Tunnel Innovation and Opportunity. Toronto, ON, Canada, 2002.

[36] ZHAO X, PAUL YOUNG R. Numerical modeling of seismicity induced by fluid injection in naturally fractured reservoirs [J]. Geophysics, 2011, 76(6): WC169. DOI: https://doi.org/10.1190/geo2011-0025.1.

[37] ZHOU J, ZHANG L, BRAUN A, et al. Numerical modeling and investigation of fluid-driven fracture propagation in reservoirs based on a modified fluid-mechanically coupled model in two-dimensional particle flow code [J]. Energies, 2016, 9(9): 699. DOI: https://doi.org/10.3390/en9090699.

[38] PFC 5.0 manual [M]. Minneapolis, MN, USA: Itasca Consulting Group, 2015.

[39] DAVY C A, SKOCZYLAS F, BARNICHON J D, LEBON P. Permeability of macro-cracked argillite under confinement: Gas and water testing [J]. Physics & Chemistry of the Earth Parts A/b/c, 2007, 32(8–14): 667–680. DOI: https://doi.org/ 10.1016/j.pce.2006.02.055.

[40] JIANG C L, QIANG S, JIANG Z Q, ZHU S Y. Permeability catastrophe of brittle rock during complete stress-strain path [J]. Zhongnan Daxue Xuebao, 2012, 43(2): 688–693. (in Chinese)

[41] MATTH I S K, BELAYNEH M. Fluid flow partitioning between fractures and a permeable rock matrix [J]. Geophysical Research Letters, 2004, 31(7): 221–237. DOI: https://doi.org/10.1029/2003GL019027.

[42] LIU H L, YANG T H, YU Q L, et al. Experimental study on fluid permeation evolution in whole failure process of tuff [J]. Dongbei Daxue Xuebao/Journal of Northeastern University, 2009, 30(7): 1030–1033. (in Chinese)

[43] LION M, SKOCZYLAS F, LED SERT B. Determination of the main hydraulic and poro-elastic properties of a limestone from Bourgogne, France [J]. International Journal of Rock Mechanics & Mining Sciences, 2004, 41(6): 915–925. DOI: https://doi.org/10.1016/j.ijrmms.2004.02.005.

(Edited by HE Yun-bin)

中文导读

基于颗粒流流–固耦合改进算法的岩石渗透性演化数值模拟研究

摘要：岩石渗透性的意义重大，构造应力和人类工程活动会对渗透性产生巨大影响。岩石内部孔压与流速分布情况的全面监测对阐明渗透性的演化机制至关重要，其在试验中难以实施，但在数值模拟中可容易实现。因此，本文采用一种离散元方法—颗粒流程序（Particle Flow Code，简称PFC）开展岩石材料渗透性行为的模拟研究。针对PFC中原流–固耦合算法的不足，对其进行改进，使改进后的算法更能体现流体在岩石裂隙中的流动优势。分别采用原算法与改进算法对三轴压缩过程中的渗透性演化进行数值模拟，对比结果表明改进算法能更好地反映试验现象。本文利用改进流–固耦合算法，进一步分析了渗流过程中的孔压和流速分布的演化情况。结果表明，孔压和流速都优先通过裂隙传递而非岩石基质。根据运移流体的能力将裂隙划分为三类： I）贯穿进口端和出口端的裂隙；II）仅与进口端连接的裂隙；III）仅与出口端连接的裂隙。I）类裂隙始终是最主要的流速和孔压的传递通道。II ）类裂隙中孔压首先增大并逐渐趋于稳定，而流速首先增大，当流体运移到裂隙终端后流速减小甚至降低为零。在III）类裂隙中，无明显的流体运移或孔压集中。

关键词：岩石力学；流–固耦合；颗粒流程序；渗透性；三轴压缩

Foundation item: Project(BK20150005) supported by the Natural Science Foundation of Jiangsu Province for Distinguished Young Scholars, China; Project(2015XKZD05) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2017-02-24; Accepted date: 2017-04-05

Corresponding author: YANG Sheng-qi, PhD, Professor; Tel: +86–516–83995856; Fax: +86–516–83995678; E-mail: yangsqi@ hotmail.com