增量选择解码前传中继系统的二阶统计特性

刁新颖，张曙

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001)

摘要：针对解码中继系统由中继译码错误产生的系统性能降低以及频谱利用率低的问题，提出选择中继和增量中继相结合的增量选择解码前传 (Incremental selection decode-and-forward，ISDF) 中继系统，并且研究ISDF系统的中断性能，分析系统的二阶统计特性(平均电平通过率和平均中断时间)。在Nakagami-m衰落信道下，给出ISDF中继系统的中断概率、平均电平通过率和平均中断时间的闭合表达式。将ISDF系统与选择解码中继系统进行比较。研究结果表明：ISDF系统明显地提高了系统的性能，降低了中断概率；当切换门限和中断门限相等时，中断性能最优；ISDF系统的平均电平通过率和平均中断时间依赖于切换门限与中断门限的选择；ISDF系统性能受到源到中继链路和中继到目的地链路中较差的链路所限制。

关键词：协作分集；增量中继；选择解码前传；平均电平通过率；平均中断时间

中图分类号：TN929.5          文献标志码：A         文章编号：1672-7207(2012)06-2179-06

The second order statistics of incremental selection decode-and-forward relay system

DIAO Xin-ying，ZHANG Shu

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract: Aiming at the problems of the fixed decode-and-forward relay system, incremental selective decode-and-forward (ISDF) relay system was proposed, which was composed of incremental relaying (IR) and selection relaying (SR). The outage and the second order statistics (the average level crossing rate and the average output duration) of the ISDF relay system were analyzed. Closed-form expressions for the outage probability, the average level crossing rate and the average output duration were given. The results show that the ISDF relay system significantly improves outage performance in comparison with the SR protocol. The outage performance is optimal when the switching threshold is the same as outage threshold. The average level crossing rate and the average output duration are highly dependent on the switching threshold and outage threshold. The performance of the ISDF system depends on the worst of the source-relay channel and the relay-destination channel.

Key words: cooperative diversity; incremental relaying; selection decode-and-forward; average level crossing rate; average output duration

在协作分集通信系中，多个协作用户转发源用户的信息，接收端可以获得多个相互独立的信号，然后合并接收信号，获得分集增益^[1]。Laneman等^[2]提出了3种协作策略：固定中继(Fixed relaying, FR)、选择中继(Selection relaying, SR)和增量中继(Incremental relaying, IR)。所有以上中继策略都是基于放大前传(Amplify-and-forward，AF)或者解码前传(Decode-and- forward，DF)方案。在固定解码前传(Fixed decode-and- forward，FDF)中继系统中，当有些符号在中继节点解码错误时，仍然被转发至接收端。选择解码前传^[3](Selection decode-and forward, SDF)中继系统在中继可以正确解码时，才由中继转发源信号，克服了FDF中继系统存在的问题。但是，当接收端可以正确解码直接链路信号时，SDF系统仍然保持中继链路工作，降低了系统的频谱利用率。而IR方案^[4]中，接收端通过检测直接链路接收的信号，判断能否正确解码，若信道情况良好，则无需中继，能够提高系统的频谱利用率。比特错误率是衡量系统性能的常用度量标准，人们对各种协作分集系统的误码率有了很多的研究^[5-8]。但是，在误码率相等的情况下，错误连续发生还是随机发生，决定了通信系统要采取的应对措施。为此，引入平均电平通过率(Average level crossing rate, LCR)和平均中断时间(Average outage duration, AOD)。电平通过率和平均中断时间是衡量系统二阶统计特性的重要指标。应用莱斯公式研究系统的LCR和AOD，需要对接收机输出信号幅度与其时间微分的联合概率密度函数(Joint probability density function, JPDF)进行积分^[9]。而对于各支路独立非同分布的系统，要知道JPDF是非常困难的，所以，目前针对协作分集系统的二阶统计特性的研究还较少，Chau等^[10]研究了Nakagami-m衰落信道下放大前传中继系统的LCR和AOD。Zhan等^[11]研究了Rayleigh衰落信道下增量解码中继系统的LCR和AOD，Talha等^[12]研究了Rayleigh信道下AF协作分集系统的二阶统计特性。在此，本文作者研究ISDF系统的中断性能和二阶统计特性，并给出Nakagami-m衰落信道下ISDF系统的中断概率、LCR和AOD的闭合表达式。

1  模型建立

协作分集系统由1个源S、1个目的地D和1个中继R组成，如图1所示，都配置单天线，并且所有链路的高斯白噪声都具有同样的方差N₀。在S与D之间，S与中继R之间以及中继R与D之间的信道衰落系数分别记作f，h₁和h₂，每条支路接收信号的包络都服从Nakagami-m分布。Nakagami-m衰落过程的概率密度函数(PPF)(Probability density function, PDF)，记为f_α(α)。

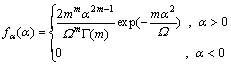    (1)

其中：Ω=E[α²]；m≥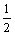，为信道形状因子；Rayleigh衰落为Nakagami-m衰落在m=1时的特例；Γ(·)为伽马函数。伽马函数由下面积分定义：

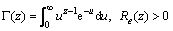       (2)

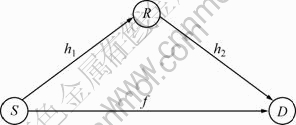
图1 协作分集的系统框图

Fig.1  Illustration of cooperative diversity network

Nakagami-m衰落过程的累积分布函数(Cumulative density function, CDF)，记为F_α(α)。

        (3)

其中，Γ(·,·)表示第一类不完全伽马函数，定义为：。

协作的策略为：在目的地和中继处都设置切换门限α_th，源节点S先向目的地和中继发送信号，接收端检测接收到的直接链路的信号包络α_f，若α_f≥α_th，则目的地直接解码直接链路的信号，无需中继；若α_f＜α_th，则反馈1个失败应答信号，中继检测接收到的信号包络α₁，若α₁≥α_th，中继则解码并转发源信号，接收端只接收中继支路信号。若α₁＜α_th，中继则不转发信号，接收端只接收直接链路的信号。

在本文协作策略下，接收端可以根据信道条件在直接链路和2个中继链路之间切换，同时，检测在目的端和中继节点都要进行。因此，本策略在增加协作选择的自由度的同时，也增加了分析的复杂性。

2  系统性能分析

为了分析系统性能，首先要得到系统输出信号包络α的CDF。设目的端接收机在t=nT (T是传输时隙持续时间)时刻输出信号包络记作z_n，有：

         (4)

其中：α_fn和α_2n分别为接收端在t=nT时刻接收到的直接链路和中继链路信号的包络。

根据系统模型，事件(z_n=α_fn)表示此时刻只有直接链路工作，它的充分必要条件为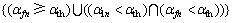，α_1n为中继端t=nT时刻接收到的信号包络。事件(z_n=α_2n)表示中继解码转发源信号，其充分必要条件是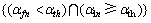。由于这几个概率都依赖于预先设置的切换门限α_th，通过分析α与α_th的关系，可以得到以下2种情况下输出信号包络α的CDF。

(1) 当α≤α_th时，有

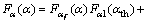
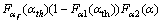        (5)

(2) 当α＞α_th时，有

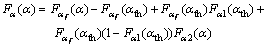  (6)

根据以上得到的系统输出信号包络α的CDF，就可以得到α的概率密度函数f_α(α)。

2.1  中断性能分析

系统的中断概率定义为接收信号包络低于中断门限R的概率，可以根据系统模型，通过α的CDF得到。根据式(3)和式(5)可以得到当R≤α_th时中断概率：

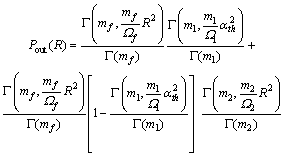 (7)

其中：m，m₁和m₂分别为源到目的地、源到中继和中继到目的地信道的形状因子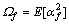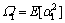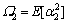；；；。根据式(3)和式(6)可以得到当R＞α_th时的中断概率：

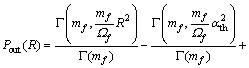
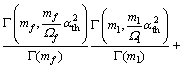
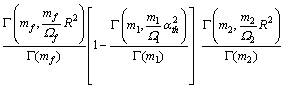(8)

2.2  LCR和AOD

LCR定义为单位时间内接收信号沿正向或负向穿越一个给定值(即中断门限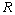)的次数，AOD定义为接收信号低于给定值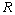的平均时间，记为N(R)。

直接应用莱斯公式^[13]得LCR：

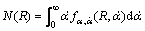          (9)

式中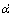：为α的时间微分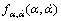；为α和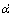的JPDF。根据文献[14]提出的分析切换驻留合并系统的LCR和AOD的方法，讨论ISDF中继系统的LCR。

根据系统模型，可以得到系统输出包络α和其时间导数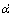的JPDF，记为。

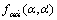(10)

其中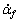：为α_f的时间微分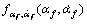；为α_f和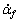的JPDF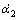；为α₂的时间微分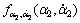；为α₂和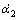的JPDF。因此，可以得到系统的N(R)为：

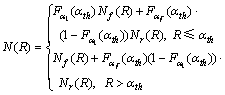    (11)

其中：N_f(R)表示直接链路工作时的LCR；N_r(R)表示中继工作时系统的LCR；N_r(R)和N_f(R)都是单支路Nakagami衰落信道的LCR，在文献[15]中已给出：

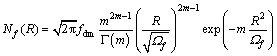(12)

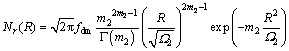(13)

其中：f_dm为最大多普勒频移。与应用莱斯公式对联合概率密度函数进行积分的传统方法相比，式(11)给出的表达式降低了传统求LCR的复杂性，更易实现。根据式(3)可以得到：

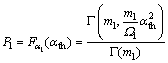       (14)

      (15)

根据文献[13]给出的AOD的定义，系统的平均中断时间T(R)可以通过下式得出：

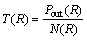             (16)

3  仿真结果与分析

根据前面的理论分析，对Nakagami衰落信道下ISDF中继系统的中断概率P_out(R)、二阶统计特性LCR和AOD进行仿真分析，并与SDF中继系统的性能进行比较。

在实际通信时，要选取合适的切换门限α_th，切换门限α_th选取过低时，系统基本上处于只有直接链路工作的状态，无法达到提高系统性能的目的；而α_th过高时，系统频繁切换导致时延过大。图2描述了R=0 dB时，中断概率与切换门限的关系。由图2可以看到：当α_th≤R时，中断概率随着切换门限的增大而降低，当α_th＞R时，随着切换门限的增大，系统的中断概率也增大。所以，系统的中断概率存在最小值，即当R=α_th时，中断性能最佳。

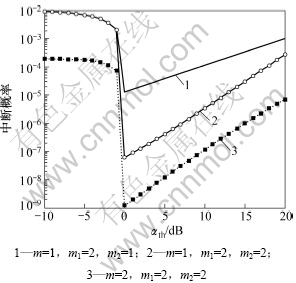
图2  ISDF系统的中断概率与切换门限α_th的关系

Fig.2  Relationship between outage of ISDF system and switching threshold α_th

图3所示为ISDF和SDF系统的中断概率比较，仿真条件为：R=α_th=0 dB。从图3可以看到：ISDF系统的中断性能明显优于相同信道条件下SDF系统中断性能；当m=1时，ISDF中继系统在m₁=2，m₂=1和m₁=1，m₂=2的2条中断概率曲线是重合的，这说明源到中继信道h₁和中继到目的地信道h₂ 2条支路中对系统中断性能的影响是相同的。并且当m₁=6和m₂=1时，系统的中断性能优于m₁=2和m₂=1条件下的中断性能，但是改善效果并不明显。

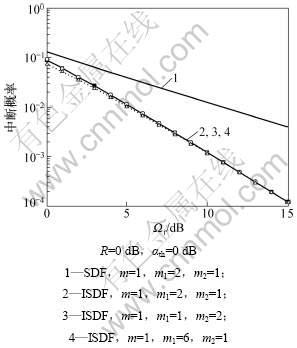
图3  ISDF和SDF系统的中断概率比较

Fig.3  Comparison of outage of ISDF and SDF system

图4所示为ISDF系统中断概率与m₂的关系。仿真条件为：R=α_th=0 dB，m=1，m₁=4。从图4可以看出，当m₁＞m₂时，系统的中断性能随着m₂的增大改善明显；当m₁＜m₂，增大m₂时系统的中断性能改善不明显。仿真结果说明系统性能受到了源到中继信道h₁和中继到目的地信道h₂ 2条支路中性能比较差的支路的制约。

ISDF和SDF系统的归一化N(R)/f_dm与中断门限R和切换门限α_th之间的关系分别如图5和图6所示，仿真条件为Ω_f=10 dB。从图5和图6可以看到：在m=1，m₁=6，m₂=2，R≤α_th时，ISDF系统的N(R)随着中断门限的升高而升高，并小于SDF系统的N(R)；并且当R=α_th时，ISDF系统的N(R)发生跳变。在R≤α_th，m₁=m₂时，ISDF系统的归一化N(R)明显要优于m₁≠m₂条件下的N(R)。

ISDF和SDF系统的归一化平均中断时间AOD(T(R))与中断门限R和切换门限α_th之间的关系分别如图7和图8所示。仿真条件为Ω_f=10 dB。从图7和图8可以看到：当R=α_th时，ISDF系统的T(R)发生跳变。在m=1，m₁=6，m₂=2，α_th←R时，ISDF系统的T(R)小于相同衰落信道条件下SDF系统的T(R)，并且在m₁=m₂时，ISDF系统的归一化T(R)明显要比m₁≠m₂条件下的小；当切换门限α_th>>R时，基本上只有直接链路工作，所以，此时系统的T(R)趋近于1个常数，而不再随着切换门限的变化而变化。

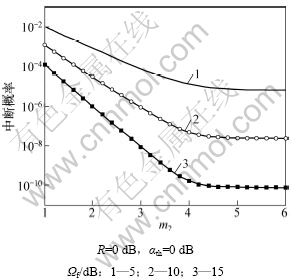
图4  ISDF系统的中断概率与m₂的关系

Fig.4  Relationship between outage of ISDF system and versus m₂

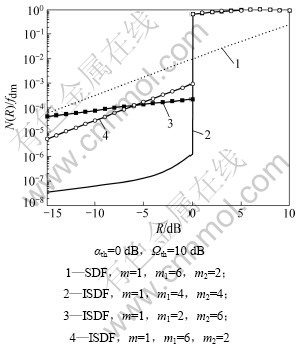
图5  ISDF和SDF系统的归一化LCR与中断门限R的关系

Fig.5  Relationship between normalized LCR of ISDF and SDF system and outage threshold R

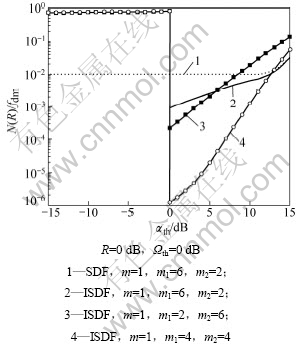
图6  ISDF和SDF系统的归一化LCR与切换门限α_th的关系

Fig.6  Relationship between average normalized LCR of ISDF and SDF system and switching threshold α_th

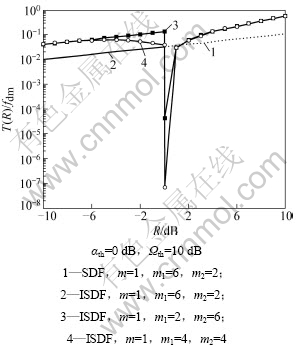
图7  ISDF和SDF系统的归一化AOD与中断门限R的关系

Fig.7  Relationship between normalized AOD of ISDF and SDF system and outage threshold R

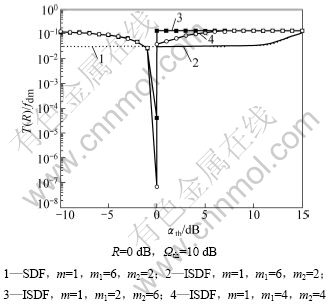
图8  ISDF和SDF系统的归一化AOD与切换门限α_th的关系

Fig.8  Relationship between average normalized AOD of ISDF and SDF system and switching threshold α_th

4  结论

 (1) 研究了ISDF中继系统，目的端和中继可以根据信道状态选择传输链路。在信道为Nakagami-m衰落时，给出了系统中断概率、二阶统计特性LCR和AOD的闭合表达式。

(2) ISDF中继系统可以提高系统的中断性能；当切换门限α_th与中断门限R相等时，系统的中断性能最佳。

(3) ISDF中继系统的LCR和AOD不仅取决于中断门限，也依赖于切换门限的选取。从系统LCR角度选择最佳切换门限时，应该是切换门限略大于中断门限。从系统AOD角度选择最佳切换门限时，应该是切换门限略小于中断门限。而在实际通信时，可以根据通信要求选取适当的门限。

(4) ISDF中继系统的中断性能和二阶统计特性受到了源到中继链路和中继到目的地链路中较差的链路所限制。当源到中继和中继到目的地的信道参数m相等时，系统的二阶统计特性最佳。

参考文献：

[1] Nosratinia A, Hunter T E, Hedayat A. Cooperative communication in wireless network[J]. IEEE Communications Magazine, 2004, 42(10): 74-80.

[2] Laneman J N, Tse D N C, Wornell G W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior[J]. IEEE Transaction on Information Theory, 2004, 50(12): 3062-3080.

[3] CAI Chun-xiao, CAI Yue-ming, HU Jun-quan, et al. Performance analysis of selection decode-and-forward relay networks over Nakagami-m fading channels[C]//Proceedings of 2010 IEEE 12th International Conference on Communication Technology. New Jersey, USA, 2010: 183-186.

[4] Ikki S S, Ahrned M H. Performance analysis of incremental- relaying cooperative-diversity networks over Rayleigh fading channels[J]. IET Communications, 2011, 5(3): 337-349.

[5] Senaratne D, Tellambura C. Unified exact performance analysis of two-hop amplify-and-forward relaying in nakagami fading[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1529-1534.

[6] Hasna M O, Alouini M S. A performance study of dual-hop transmissions with fixed gain relays[J]. IEEE Transaction on Wireless Communications, 2004, 3(6): 1963-1968.

[7] Ikki S S, Ahrned M H. Performance analysis of adaptive decode-and-forward cooperative diversity networks with best-relay selection[J]. IEEE Transactions on Communications, 2010, 58(1): 68-72.

[8] DUAN Dong-liang, YANG Liu-qing, Principe J C. Cooperative diversity of spectrum sensing for cognitive radio systems[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3218-3227.

[9] Ko Y C, Abdi A, Alouini M S, et al. Average outage duration of diversity systems over generalized fading channels[C]//2000 IEEE Wireless Communications and Networking Conference. Chicago, United States, 2000: 216-221.

[10] Chau Y A, Huang K Y. Channel statistics and performance of cooperative selection diversity with dual-hop amplify-and- forward relay over Rayleigh fading channels[J]. IEEE Trans Wireless Commun,2008, 7(5): 1779-1785.

[11] ZHAN Wei-xu, WANG Gui-juan, ZHANG Guang-chi, et al. Level crossing rate and average outage duration of incremental DF relay channel[C]//5th International Conference on Wireless Communications, Networking and Mobile Computing. New Jersey, USA: IEEE Computer Society, 2009.

[12] Talha B, Primak S, Patzold, M. On the statistical properties of equal gain combining over mobile to mobile fading channels in cooperative networks[C]//IEEE International Conference on Communications. New Jersey, USA: Institute of Electrical and Electronics Engineers Inc, 2010.

[13] Stüber G L. Principles of mobile communication[M]. 2nd ed. Massachusetts: Kluwer Academic Publishers, 2000: 606-617.

[14] YANG Lin, Alouini M S. Average level crossing rate and average outage duration of switched diversity systems[C]//IEEE Global Telecommunications Conference. Institute of Electrical and Electronics Engineers Inc, 2002: 1420-1424.

[15] Ali A, Kyle W, Alien B H, et al. Comparison of the level crossing rate and average fade duration of Rayleigh, Rice, and Nakagami fading models with mobile channel data[C]//IEEE VTS Fall VTC. New Jersey: IEEE Piscataway, 2000: 1850-1857.

(编辑 陈灿华)

收稿日期：2011-05-25；修回日期：2011-08-15

基金项目：国防科学技术工业委员会基础研究基金资助项目(40106030503)；国家自然科学基金资助项目(60875020)

通信作者：刁新颖(1980-)，女，河北沧州人，博士研究生，从事无线通信协作分集技术的研究；电话：0451-82544465；E-mail：diaoxinying@hrbeu.edu.cn