DOI: 10.11817/j.issn.1672-7207.2016.01.035
考虑渗流-应力耦合作用的层状盐岩界面裂缝扩展模型研究
贾善坡1, 2,杨建平3,谭贤君3,王越之1
(1. 长江大学 岩土力学与工程研究中心,湖北 荆州,434023;
2. 中石油华北油田勘探开发研究院,河北 任丘,062552;
3. 中国科学院 武汉岩土力学研究所,湖北 武汉,430071)
摘要:针对中国地下油气储库建设中所出现的含夹层盐岩问题,基于黏结裂缝模型,构建一种可以考虑层状盐岩地层界面启裂、裂隙扩展和流体渗漏的黏结单元,导出地层界面损伤演化方程、裂隙扩展准则以及缝内流体流动方程,建立考虑渗流-应力耦合作用的层状盐岩界面裂缝扩展模型,通过典型算例验证模型的有效性。研究层状盐岩地层界面启裂与裂隙扩展过程。研究结果表明:地层的渗透性和裂缝面漏失系数对地层界面裂隙扩展有明显影响,地层渗透性系数越小,地层开裂程度越大;而裂缝面漏失系数越大,地层开裂程度越弱,但流体渗漏程度加大。
关键词:层状盐岩;储气库;裂缝扩展;渗漏;有限元
中图分类号:TE822 文献标志码:A 文章编号:1672-7207(2016)01-0254-08
Analytic model for interface crack propagation of salt rock with interlayer under coupled mechanical-hydrological environment
JIA Shanpo1, 2, YANG Jianping3, TAN Xianjun3, WANG Yuezhi1
(1. Research Center of Geomechanics and Geotechnical Engineering, Yangtze University, Jingzhou 434023, China;
2. Exploration and Development Research Institute of Huabei Oilfield, China National Petroleum Corporation,
Renqiu 062552, China;
3. Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China)
Abstract: According to the reality of bedded rock salt and clay interlayer for oil or gas storage in China, the cohesive element built in bedded salt rock was used to simulate the initiation, propagation and fluid seepage resulted from hydraulic loading by the cohesive zone model. The damage evolution equation, crack propagation criterion and fluid flow equation of interlayer were established. Based on the fluid-solid coupling theory of rock, the coupled interface crack propagation model of salt rock with interlayer was put forward and a typical example of application was presented to verify the validity of the model. Then, the crack propagation process of salt cavern was studied and the influence law of pore pressure, injection pressure and crack propagation was discussed in different conditions. The results show that the permeability of rock and leakage coefficient of crack has significant effects on the condition of crack propagation. The condition of crack aggravates with low permeability of rock and reduces with high leakage coefficient.
Key words: bedded rock salt; storage cavern; crack propagation; seepage; finite element
为了克服地上油气储备的不足,许多国家利用地下盐穴储存油气。盐岩被公认为是油气储存的理想介质,用于国家战略能源储备和商业油气储备。与国外大量存在的“盐丘型”储层条件不同,我国盐岩地层的基本特点是盐岩层多、单层厚度小,盐岩体中一般含有众多夹层。尽管盐岩本身的渗透率极低,但由于盐岩在造腔和运营过程中受交变载荷影响,导致腔体围岩的渗透率提高,同时夹层还存在变形不协调而产生层面滑动,使得层状盐岩储气库可能存在渗漏的风险,因此,密封性成为储气库安全评价的重要指标之一。国内外对层状盐岩渗透性研究刚刚起步,尤其对层状岩盐的渗透性和含夹层的盐穴储气库的渗漏研究甚少。HUNSCHE [1]提出了损伤扩容准则,认为当应力状态处于压缩-扩容边界之上时,盐岩损伤程度不断增强,盐岩的渗透系数增大几个数量级。POPP等[2-3]测试了盐岩在三轴加载过程中的渗透率演化和超声波速变化,对加载过程中盐岩微裂隙扩展演化进行了研究;李银平等[4]基于盐岩-硬石膏界面力学特性室内试验研究成果,结合现场盐岩层钻孔高压压水试验,对云应地区储气库密闭性进行了研究。梁卫国等[5]认为盐穴储气库在运行过程中由于盐岩和夹层间存在力学差异和变形不协调对盐穴密封性的影响比较显著,提出了多夹层盐穴储气库极限运行压力的计算方法。黄小兰等[6]从现场气密性测试、盐岩及夹层扫描电镜试验等多方面对潜江地区层状盐岩天然气储库密闭性进行了研究。周宏伟等[7]对湖北云应含夹层盐岩进行了渗透性测试,测得的渗透率范围为10-16~10-18 m2。彭瑞东等[8]借助可以进行原位加载下实时观测的SEM实验系统,对载荷作用下层状盐岩开裂破坏时的裂纹扩展规律进行了研究,探讨了层状盐岩破坏的细观机制。张耀平等[9]建立了层状盐岩等效边界渗漏模型和层状盐岩固-气耦合模型,但这些模型无法反映夹层界面的开裂及其对渗透性的影响。含夹层盐岩内建造盐穴油气储库是一项艰巨的工程,不仅要考虑夹层不协调变形所引起的层间裂隙扩展、溶腔稳定性问题, 而且要充分考虑夹层及层面裂隙的渗透性所引起的密封性问题,因此,夹层和层间裂隙的渗漏是评价含夹层盐岩储气库密封性的重要指标。本文作者在张耀平等[9]研究基础上,采用以节点位移和孔隙压力为自由度的黏结单元,建立渗流-应力耦合作用下层状盐岩界面裂缝扩展模型,并进行相应的数值模拟,研究层状盐岩裂缝扩展过程及流体渗漏规律。
1 层状盐岩界面裂缝扩展模型
1.1 地层界面本构关系
地层界面裂缝扩展通过黏结单元来描述,启裂前界面应力-应变满足弹性关系:
 (1)
(1)
式中:t为界面应力矢量;tn,ts和tt分别为法向和2个切向承受的应力,其中下标n,t和s分别为单元的法向和2个切线方向单元,分别对应于Ⅰ型断裂、Ⅱ型和Ⅲ型断裂;K为单元刚度矩阵;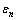 ,
, 和
和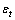 分别为法向和2个切向应变。界面破坏起始是指地层刚度开始恶化,目前有多种判定准则,例如最大应变准则、平方应变准则、最大应力准则、平方应力准则等。采用平方应力准则来描述层状盐岩的启裂行为[10],当界面3个方向承受的应力与其对应临界应力的比值的平方和达到1时,单元开裂并扩展,即
分别为法向和2个切向应变。界面破坏起始是指地层刚度开始恶化,目前有多种判定准则,例如最大应变准则、平方应变准则、最大应力准则、平方应力准则等。采用平方应力准则来描述层状盐岩的启裂行为[10],当界面3个方向承受的应力与其对应临界应力的比值的平方和达到1时,单元开裂并扩展,即
 (2)
(2)
式中: 为界面的法向临界拉应力;
为界面的法向临界拉应力; 和
和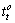 分别为2个切向的临界拉应力;
分别为2个切向的临界拉应力; 表示只取正整数。
表示只取正整数。
地层界面的本构关系可表示为黏结力t与局部坐标系下位移 之间的关系函数:
之间的关系函数:
 (3)
(3)
现有的一些本构关系都是唯象的,是通过试验数据得到的经验公式例如梯形关系、线性-抛物线关系、指数关系、双线性关系等。ALFANO[11]对它们进行比较计算,认为双线性模型能够兼顾计算精度和计算效率的要求。本文选用双线性本构关系(见图1):

图1 黏结单元双线性本构关系
Fig. 1 Bilinear constitutive equation for cohesive element
 (4)
(4)
式中:D为损伤变量;K为罚刚度; ,
,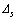 和
和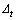 分别为地层界面的法向和2个切向位移。
分别为地层界面的法向和2个切向位移。
1.2 地层界面损伤演化准则
在混合加载模式下,地层界面的损伤演化准则定义为以位移变化的形式:
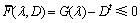 (5)
(5)
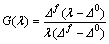 (6)
(6)
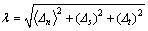 (7)
(7)
其中: 为地层界面启裂位移;
为地层界面启裂位移; 为界面失效位移;
为界面失效位移; 为损伤变量随时间的变化量,0≤
为损伤变量随时间的变化量,0≤ ≤1,当
≤1,当 >
> 时,发生启裂;当
时,发生启裂;当 ≥
≥ 时,Dt=1,材料完全断裂;黏结力
时,Dt=1,材料完全断裂;黏结力 。黏结裂缝模型示意图见图2。
。黏结裂缝模型示意图见图2。
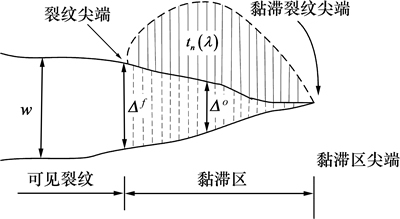
图2 黏结裂缝模型示意图
Fig. 2 Diagram of cohesive model for hydraulic fracture
式(6)中 是起始破坏时对应节点的张开量,是由起始破坏准则决定的。采用平方应力准则时单元起始破坏对应的张开量为
是起始破坏时对应节点的张开量,是由起始破坏准则决定的。采用平方应力准则时单元起始破坏对应的张开量为

 (8)
(8)
式中: ;
; ;
;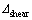 为2个剪切方向的位移矢量和,
为2个剪切方向的位移矢量和, 。式(6)中
。式(6)中 反映地层界面在复杂应力状态下的断裂能量释放率。,其计算是一个比较复杂的过程。在混合加载模式下,通常使用能量释放率和断裂韧性来描述裂纹扩展准则。当能量释放率G超过临界值
反映地层界面在复杂应力状态下的断裂能量释放率。,其计算是一个比较复杂的过程。在混合加载模式下,通常使用能量释放率和断裂韧性来描述裂纹扩展准则。当能量释放率G超过临界值 时,裂纹开始扩展,选用BENZEGGAGH和KENANE提出的准则:
时,裂纹开始扩展,选用BENZEGGAGH和KENANE提出的准则:
 (9)
(9)
式中: 和
和 分别为Ⅰ和Ⅱ型断裂韧度;
分别为Ⅰ和Ⅱ型断裂韧度; 为总能量释放率;
为总能量释放率; 和
和 分别为Ⅰ和Ⅱ型能量释放率;
分别为Ⅰ和Ⅱ型能量释放率; 为模型参数。在双线性本构关系中,
为模型参数。在双线性本构关系中, ,可得:
,可得:
 (10)
(10)
 (11)
(11)
其中: 为混合模式率,
为混合模式率, 。
。
1.3 裂缝界面流体运动模型
应力对裂隙渗流场的影响主要是改变了裂缝的宽度,从而使裂缝的渗透性发生变化。以往在研究裂缝渗流时仅考虑流体沿着裂缝切向流动[12],本文定义流体除了可以沿着裂缝切向流动外,还可以横穿裂缝面渗流。
流体在裂缝内的切向流动采用牛顿流公式进行描述。流体流动依赖于随时间t变化的裂缝张开度w,用方程表示为[13]
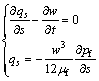 (12)
(12)
式中:qs为流体沿裂缝切向的流量;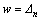 为界面裂缝张开度;
为界面裂缝张开度; 为流体的黏性系数;pf为流体压力。
为流体的黏性系数;pf为流体压力。
流体沿裂缝面法向的流量qn,包括流体流进单元上下表面的流量之和,即
 (13)
(13)
式中:q1和q2分别为流体进入单元上、下表面的流量;c1和c2分别为单元上、下表面滤失系数;p1和p2为单元上、下表面孔隙压力。
1.4 地层不连续界面的模拟
使用无厚度黏结单元模拟地层界面开裂问题的优点在于能够将启裂和裂隙扩展2个过程统一在1个模型中进行计算;另外,黏结单元可以方便地嵌入到地层单元之间,计算效率高。下面以平面6节点渗流-应力耦合黏结单元(见图3)为例进行说明。图3中,节点1,4和5位置重合,节点2,3和6位置重合;节点1~4用于描述裂隙的变形和裂缝面渗漏,其自由度为位移和孔隙压力;节点5和6用于描述裂隙内流体流动,其自由度仅为流体压力。

图3 考虑流-固耦合效应的零厚度裂缝单元
Fig. 3 Zero-thickness crack element with hydro-mechanical coupling
考虑地层孔隙压力和变形非线性特点,并与界面模型相配合,在裂隙可能发展区域(四边形等参单元之间)预先布置黏结单元,见图4。通过黏结单元的位移模拟裂纹的张开与闭合,黏结单元外部节点(节点1~4)与地层单元连接,并且与临近的地层单元公用节点[14]。

图4 裂缝单元与周围地层单元连接示意图
Fig. 4 Diagram of connecting cohesive elements to neighboring elements
2 计算模型的验证
为了验证模型的有效性,以典型的裂隙扩展算例进行对比分析[15]。岩石为非渗透介质,x轴为裂隙扩展方向(图5),模型周边法向位移约束,具体计算参数见表1。注入流体流量为Q0=0.001 m3/s,计算结果如图6~8所示。对于张开位移和裂缝长度,其数值解与理论解较吻合;对于注入压力,在岩石开裂之后其数值解与理论解大致吻合。开裂前存在一定的差别,这主要是数值计算的初始条件引起,注入点初始水压为0 MPa,流体注入预设的黏结单元后,压力迅速增加导致裂缝产生和扩展;随着裂隙逐渐向深部延伸,压力逐渐降低并趋于稳定。该算例表明:采用本文方法处理地层界面开裂问题是可行的,可以实现复杂的多场耦合计算。
表1 计算参数
Table 1 Main parameters for calculation


图5 数值验证模型
Fig. 5 Testing model

图6 裂缝张开度的理论解与数值解比较曲线
Fig. 6 Comparison of crack opening between numerical and analytical solution
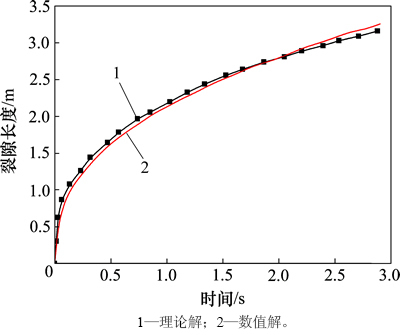
图7 裂缝长度的理论解与数值解比较
Fig. 7 Comparison of crack length between numerical and analytical solution
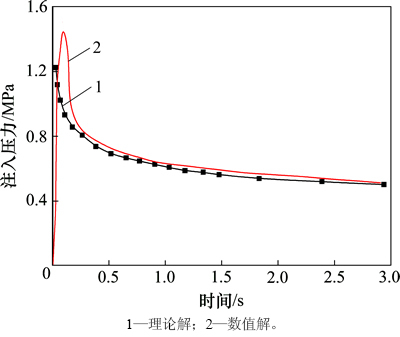
图8 注入压力的理论解与数值解比较曲线
Fig. 8 Comparison of injection pressure between numerical and analytical solution
3 工程应用
3.1 计算模型及参数
储气库投入运行前要经过密封性试验,重点针对地质因素的密封性进行检测。密封性测试方法是向腔体注水憋压,通过观测压力变化和液体漏失情况判断是否存在腔体漏失(图9)。计算模型长度为1.0 m,宽度为0.4 m;右边界和底边界法向位移约束,上边界施加地应力10 MPa,左边界施加内压10 MPa;在节点A处施加流量边界。计算参数如表2所示。

图9 计算模型示意图
Fig. 9 Sketch of physical model
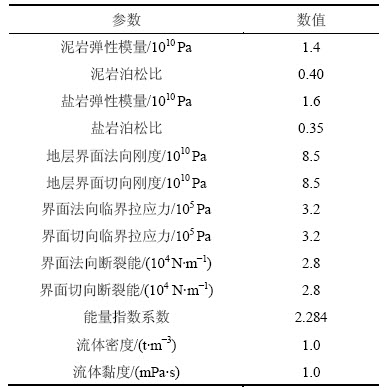
表2 层状盐岩计算参数
Table 2 Main parameters for calculation of salt rock with interlayer
3.2 地层非渗透条件下计算结果
将层状盐岩看作非渗透介质,流体仅沿着裂缝单元切向流动,计算结果如图10~11所示。
当地层界面应力达到启裂条件后,流体迅速进入裂缝中,流体仅沿着裂隙开裂方向渗漏。图10所示为地层裂缝张开度随随时间的变化曲线。从图10可见:在0~5 s内,注入流量逐步增加到5.0×10-6 m3/s,地层界面启裂,裂隙张开速率随时间逐渐增大;在5~10 s内,注入流量保持恒定,裂隙张开度随时间呈线性增大趋势;在10~15 s内,注入流量逐步减小到0 m3/s,裂隙张开速率随时间逐渐减小;在15~20 s内,注入流体流量为0 m3/s,裂隙停止扩展。
图11所示为注入压力随时间的变化曲线。从图11可见:储库内压随着流体的注入而逐渐增大,当内压达到10.5 MPa时,地层界面启裂;此后,注入压力趋于稳定值10.3 MPa,裂隙逐渐向深部扩展。通过分析发现:当裂隙失稳扩展时,储库内压并不下降,裂隙内流体压力基本是全水头(储库内压一致),因而裂隙一旦失稳,就会很快扩展。
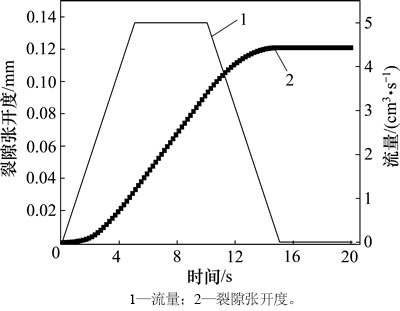
图10 裂隙张开度随时间的变化曲线
Fig. 10 Relationship among crack opening displacement, rate of flow and time
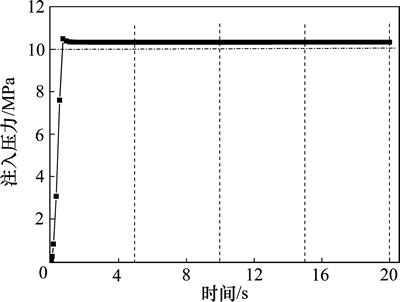
图11 注入压力随时间的变化曲线
Fig. 11 Variation of injection pressure with time
3.3 地层渗透条件下计算结果
将层状盐岩看作渗透介质,泥岩渗透系数为1.0×10-9 m/s,孔隙度为0.06;盐岩渗透系数为8.418×10-10 m/s,孔隙度为0.01。考虑流体沿着裂隙面法向渗漏,漏失系数为5.87×10-13 m3/(Pa·s),初始孔隙压力为5.0 MPa。
图12所示为考虑地层渗透条件下裂隙张开度沿裂缝长度的变化曲线。从图12可见:5 s后裂隙张开度为0.011 mm,10 s后裂隙张开度为0.052 mm,15 s后裂隙最大张开度为0.034 mm。由于考虑了地层的渗透性,在0~10 s内,裂隙是逐步扩展的,而在10~20 s内,注入流量减小导致裂缝逐渐闭合。
图13所示为考虑地层渗透条件下裂隙张开度随时间的变化曲线。从图13可见:考虑地层为渗透介质时,随着流体的注入,地层界面在4 s时启裂,12 s时裂隙张开度达到最大值,此后,由于流体注入量减少致使裂隙逐步趋于闭合。通过比较地层是否渗透可以发现:考虑地层渗透时裂隙扩展情况明显与非渗透时不同,裂隙的长度和张开度均明显小于非渗透性条件的计算结果。由此可见:在研究储库流体渗漏机理时,地层及其界面的渗透性不可忽视。

图12 裂隙张开度沿裂缝长度的变化曲线
Fig. 12 Variation of crack opening displacement across fracture length

图13 不同地层条件下裂隙张开度随时间的变化曲线
Fig. 13 Relationship between crack opening displacement and time under different formation conditions
图14所示为考虑地层渗透条件下注入压力随时间的变化曲线。从图14可见:当注入压力达到10.34 MPa时,地层界面启裂;此后,裂隙逐步扩展,注入压力趋于稳定值10.29 MPa。另外,注入流量减小致使注入压力明显下降,流体进入裂隙的阻力增大,裂隙逐渐闭合。

图14 地层渗透条件下注入压力随时间的变化曲线
Fig. 14 Variation of injection pressure of permeable formation with time
图15所示为流体渗漏量随时间的变化曲线。从图15可见:在0~5 s内,渗漏速率随时间的增大逐渐增大;在5~17.4 s内,流体渗漏量基本上随时间呈线性增大趋势;在17.4 s后,由于裂隙完全闭合,流体不再渗漏。

图15 流体渗漏量随时间的变化曲线
Fig. 15 Relationship between amount of leakage and time
3.4 裂缝法向渗漏对裂缝扩展的影响
计算条件与3.3节中的相同,仅改变裂缝的法向漏失系数,分别取漏失系数为5.87×10-12,5.87×10-13和5.87×10-14 m3/(Pa·s)进行研究,计算结果如图16和图17所示。
图16所示为不同漏失系数下注入压力随时间的变化曲线。从图16可见:漏失系数对裂缝内的流体压力有明显影响;当漏失系数较低时,随着注入流体的增加,流体沿法向漏失量较小,缝内流体压力迅速增加,裂缝逐渐扩展;若漏失系数较大,则沿法向渗漏,流体压力下降明显,达不到界面启裂条件。
图17所示为不同漏失系数下裂隙张开度随时间的变化曲线。从图17可见:当漏失系数为5.87×10-12 m3/(Pa·s)时,无裂隙产生;当漏失系数为5.87×10-13 m3/(Pa·s)时,在0~12 s内,裂隙张开度逐渐增大,最大值为0.056 mm;此后,由于注入流量的减小,裂隙逐渐闭合;当漏失系数为5.87×10-14 m3/(Pa·s)时,在0~14 s内,裂隙张开度逐渐增大,最大值为0.112 mm;此后,尽管注入流量为0 m3/s,裂隙一直处于张开状态。因此,裂缝法向漏失系数对地层界面裂隙扩展的影响不可忽视。
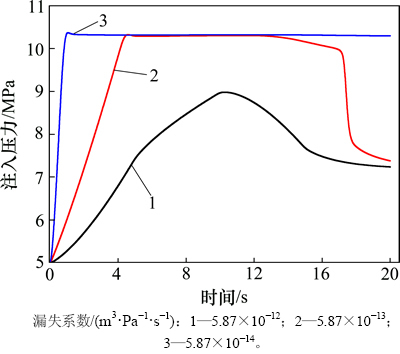
图16 不同漏失系数下注入压力随时间的变化曲线
Fig. 16 Variation of injection pressure with different leakage coefficient

图17 不同漏失系数下裂隙张开度随时间的变化曲线
Fig. 17 Variation of crack opening with different leakage coefficient
4 结论
1) 基于黏结裂缝模型,构建了以节点位移和孔隙压力为自由度的无厚度地层界面单元,利用单元刚度退化来模拟裂纹的产生与扩展。通过得到刚度损伤变量D即可以得到相应状态下单元的刚度,进而得到单元的应力、整个破坏过程的裂隙张开度与长度。
2) 基于损伤力学、断裂力学和渗流力学理论,导出了地层界面损伤演化方程以及裂缝内流体流动方程,提出了考虑渗流-应力耦合作用的层状盐岩界面裂缝扩展模型。该模型可以考虑地层界面启裂、裂缝扩展和流体渗漏,并通过算例进行了考证,验证了模型的有效性。
3) 层状盐岩裂缝内流体的法向漏失对裂缝内的流体压力有明显影响。当漏失系数较低时,流体主要沿裂缝长度范围内扩散,裂缝内流体压力迅速增加,裂缝扩展;当漏失系数较大时,缝内流体压力因为流体法向渗漏而逐渐下降,裂缝扩展速度和程度均明显降低。
4) 本文提出的模型可用于煤层气开采、油气开采领域的储层水致裂分析以及地下储气(油)库、CO2地质封存等岩石力学工程领域的盖层完整性评价方面。
参考文献:
[1] HUNSCHE U. Determination of the dilatancy boundary and damage up to failure for four types of rock salt at different stress geometries[C]// Proceedings of the 4th Conference on the Mechanical Behavior of Salt. Clausthal-Zellerfeld, Germany: Trans Tech Publications, 1996: 163-174.
[2] POPP T, KERN H. Monitoring the state of microfracturing in rock salt during deformation by combined measurements of permeability and P- and S- wave velocities[J]. Physics and Chemistry of the Earth Part A: Solid Earth and Geodesy, 2000, 25(2): 149-154.
[3] POPP T, KERN H, SCHULZE O. Evolution of dilatancy and permeability in rock salt during hydrostatic compaction and triaxial deformation[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B3): 4061-4078.
[4] 李银平, 杨春和, 罗超文, 等. 湖北省云应地区盐岩溶腔型地下能源储库密闭性研究[J]. 岩石力学与工程学报, 2007, 26(12): 2430-2436.
LI Yinping, YANG Chunhe, LUO Chaowen, et al. Study on sealability of underground energy storage in deep salt formation in Yunying area, Hubei province[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2430-2436.
[5] 梁卫国, 杨春和, 赵阳升. 层状盐岩储气库物理力学特性与极限运行压力[J]. 岩石力学与工程学报, 2008, 27(1): 22-27.
LIANG Weiguo, YANG Chunhe, ZHAO Yangsheng. Physico-mechanical properties and limit operation pressure of gas deposit bedded salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 22-27.
[6] 黄小兰, 杨春和, 陈锋, 等. 潜江地区层状盐岩天然气储库密闭性评价研究[J]. 岩土力学, 2011, 32(5): 1473-1478.
HUANG Xiaolan, YANG Chunhe, CHEN Feng, et al. Tightness evaluation test on underground energy storage in bedded salt rock formation of Qianjiang area[J]. Rock and Soil Mechanics, 2011, 32(5): 1473-1478.
[7] 周宏伟, 何金明, 武志德. 含夹层盐岩渗透特性及其细观结构特征[J]. 岩石力学与工程学报, 2009, 28(10): 2068-2073.
ZHOU Hongwei, HE Jinming, WU Zhide. Permeability and meso-structure characteristics of bedded salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2068-2073.
[8] 彭瑞东, 武志德, 周宏伟, 等. 层状盐岩中裂纹扩展规律的细观实验研究[J]. 岩石力学与工程学报, 2011, 30(S2): 3953-3958.
PENG Ruidong, WU Zhide, ZHOU Hongwei, et al. Meso- experimental investigation on crack evolution in bedded salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3953-3958.
[9] 张耀平, 曹平, 赵延林, 等. 双重介质固气耦合模型及含夹层盐穴储气库渗漏研究[J]. 中南大学学报(自然科学版), 2009, 40(1): 217-224.
ZHANG Yaoping, CAO Ping, ZHAO Yanlin, et al. Dual media model for solid-gas coupling and gas seepage in rock salt natural gas storage with interlayers[J]. Journal of Central South University (Science and Technology), 2009, 40(1): 217-224.
[10] 寇剑锋, 徐绯, 郭家平, 等. 黏聚力模型破坏准则及其参数选取[J]. 机械强度, 2011, 33(5): 714-718.
KOU Jianfeng, XU Fei, GUO Jiaping, et al. Damage lawa of cohesive zone model and selection of the parameters[J]. Journal of Mechanical Strength, 2011, 33(5): 714-718.
[11] ALFANO G. On the influence of the shape of the interface law on the application of cohesive zone models[J]. Composites Science and Technology, 2006, 66: 723-730.
[12] 孙粤琳, 沈振中, 吴越健, 等. 考虑渗流-应力耦合作用的裂缝扩展追踪分析模型[J]. 岩土工程学报, 2008, 30(2): 199-204.
SUN Yuelin, SHEN Zhenzhong, WU Yuejian, et al. Analytic model for tracing crack propagation under coupled mechanical- hydrological environment[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 199-204.
[13] CHEN Zuorong. A new enriched finite element method with application to static fracture problems with internal fluid pressure[J]. International Journal of Applied Mechanics, 2015, 7(3): 1-30.
[14] ZHOU X J, BURBEY T J. Distinguishing fluid injection induced ground deformation caused by fracture pressurization from porous medium pressurization[J]. Journal of Petroleum Science and Engineering, 2014, 121: 174-179.
[15] 王鸿勋, 张士诚. 水力压裂设计数值计算方法[M]. 北京: 石油工业出版社, 1998: 104-196.
WANG Hongxun, ZHANG Shicheng. Numerical calculation method for hydraulic fracturing design[M]. Beijing: Petroleum Industry Press, 1988: 104-196.
(编辑 陈灿华)
收稿日期:2015-01-10;修回日期:2015-03-08
基金项目(Foundation item):湖北省自然科学基金资助项目(2015CFB194);中国博士后科学基金资助项目(2014M551055);岩土力学与工程国家重点实验室开放基金资助项目(Z013007) (Project(2015CFB194) supported by the Natural Science Foundation of Hubei Province; Project(2014M551055) supported by China Postdoctoral Science Fund; Project(Z013007) supported by the Open Research Fund of State Key Laboratory of Geomechanics and Geotechnical Engineering)
通信作者:贾善坡,博士(后),副教授,从事岩石力学与工程的教学与研究工作;E-mail: jiashanporsm@163.com