DOI: 10.11817/j.issn.1672-7207.2016.03.021
抽水引起的有起始比降饱和土固结解析解
张玮鹏1,谢康和1,吕文晓2,黄大中1,吴浩1
(1. 浙江大学 滨海和城市岩土工程研究中心,软弱土与环境土工教育部重点实验室,浙江 杭州,310058;
2. 杭州科技职业技术学院 城市建设学院,浙江 杭州,311402)
摘要:研究在有起始比降的弱透水层下大面积抽水而引起的一维固结问题,采用分离变量法,获得该工况下的一维固结解析解。讨论土中渗流移动边界的运动规律,得渗流发展到达土层顶部的时间因子与起始比降的关系曲线,分析考虑起始比降后土体的一维固结和沉降特性。研究结果表明:当起始比降大于一定值时,渗流不会发展到达土层顶部,此时,弱透水层由于抽水引起的固结最终压缩量将减小,且起始比降越大,最终压缩量越小;当固结结束时,土体中孔隙水压力沿深度分布曲线为折线;而当渗流能够发展到达土层顶部时,最终压缩量为一定值,与起始比降无关,土体中的孔隙水压力沿深度分布曲线为直线。
关键词:起始比降;大面积抽水;一维固结;解析解;非达西流
中图分类号:TU46 文献标志码:A 文章编号:1672-7207(2016)03-0875-07
Analytical solution to one-dimensional consolidation of saturated soil with threshold gradient induced by groundwater pumping
ZHANG Weipeng1, XIE Kanghe1, L Wenxiao2, HUANG Dazhong1, WU Hao1
Wenxiao2, HUANG Dazhong1, WU Hao1
(1. Research Center of Coastal and Urban Geotechnical Engineering, MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;
2. Institute of Urban Construction, Hangzhou Polytechnic, Hangzhou 311402, China)
Abstract: One-dimensional consolidation was induced by groundwater pumping beneath the aquitard with threshold gradient. General analytical solutions were obtained by the method of separation of variables. The motion law of moving boundary of seepage was discussed, the relationship between the time moving boundary of seepage that reaches the top of the layer and the threshold gradient was given, and the one-dimensional consolidation and the settlement characteristics of the layer were investigated. The results show that when the threshold gradient is big enough, the moving boundary of seepage will not reach the top of the layer. The final settlement of the layer due to groundwater pumping will decrease, and the bigger the threshold gradient, the smaller the final settlement. At the end of consolidation, the curve of pore water pressure versus depth will be piecewise-linear. Whereas the moving boundary of seepage can reach the top of the layer, the final settlement is constant and irrelevant to the threshold gradient, and the curve of pore water pressure versus depth will be linear.
Key words: threshold gradient; groundwater pumping; one-dimensional consolidation; analytical solutions; non-Darcian flow
抽取地下水将导致地下水位下降,孔隙水压力减小,有效应力增加,土体发生固结而引起地面沉降。随着人类抽取地下水数量日益增加,由此引起的地面沉降问题日益严重[1-3]。地面沉降是一种严重的地质灾害,对人类生活环境等产生恶劣影响。骆冠勇等[4]对承压水减压引起的上覆土层固结进行了研究,在假定一维竖向固结的条件下推导了减压引起的固结解析解。TSENG等[5]分析了水位瞬时下降和水位随时间变化情况下自重应力对饱和土体固结的影响。TSAI[6]采用差分法研究了水位瞬时下降和水位随时间变化情况下黏滞性对饱和土体固结的影响。SHEN等[7]对上海市地下水抽取引起的地面沉降进行了数值分析,在假定三维渗流一维变形的情况下分析了地下水位、地下水抽取量与地面沉降的关系,并对今后的地面沉降进行了预测。LIU等[8]通过拉普拉斯变换获得了考虑黏弹性弱透水层因水位变化引起的一维固结解并分析了土体固结性状。谢康和等[9]获得了越流系统中水位下降弱透水层的一维固结解析解,并对固结性状进行了分析。上述研究均基于达西定律,由于达西定律以砂土渗流试验获得,并不完全适用于其他土。对于某些低渗透性饱和黏土,MILLER等[10-11]渗透试验研究证明,土中存在起始比降i0,只有当土中某点的水力坡降大于i0时,该点才会发生渗流。对于存在起始比降的土层固结问题,目前已有很多研究[12-18],但均局限于荷载引起的固结,关于抽水引起的有起始比降的土层固结研究还未见报道。为此,本文作者研究在有起始比降的弱透水土层下大面积抽水引起的固结问题,分别分析不同起始比降下渗流不能够发展到达土层顶部和能够到达土层顶部的情况。在假定渗流到达土层顶部之后上层潜水位不变的条件下,获得不同起始比降下的一维固结解析解,并分析起始比降对土体一维固结性状的影响。
1 计算模型
根据第2类越流系统,对弱透水层进行分析,其上部土层为定水头的潜水含水层,下部为透水主含水层,即大面积抽水(降水)土层,示意图如图1所示。图1中:h0为所有土层的初始水头(弱透水层顶面为基准面);H为弱透水层厚度;Ht为渗流移动边界至基准面的距离;Hc为最终渗流边界至基准面的距离;Δh为主含水层因抽水引起的水头损失;z为竖向坐标。
进行如下基本假定:1) 土体完全饱和;2) 土体是均质的;3) 土颗粒和孔隙水不可压缩;4) 土体固结变形微小;5) 土中渗流和变形是一维的;6) 在固结过程中土的竖向渗透系数kv和压缩系数a为常数;7) 弱透水层任意位置处初始水头均为h0;8) 主含水层由于大面积抽水,瞬时水位下降Δh,并由于有侧向补给及持续抽水共同作用,假定其水位下降后保持稳定;9) 潜水层由于天然补给,水头基本保持不变;10) 考虑起始比降,土中渗流方程为
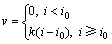 (1)
(1)
式中:v为流速;k为渗透系数;i0为起始比降(i0≥0)。
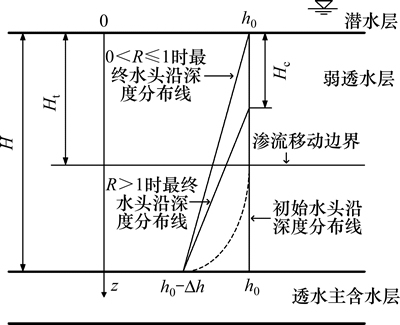
图1 大面积抽水后弱透水层中渗流发展示意图
Fig. l Schematic diagram of development of seepage in aquitard after groundwater pumping
根据求解模型及相应的基本假定,可得此条件下以水头表示的一维固结微分方程和求解条件为:
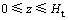 ,
,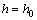 (2)
(2)
 ,
, (3)
(3)
与式(3)相应的求解条件如下。
初始条件:
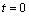 ,
,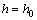 (4)
(4)
边界条件:
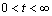 ,
,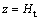 ,
, (5)
(5)
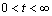 ,
,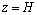 ,
,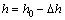 (6)
(6)
式中:cv为固结系数;h为总水头。
2 问题求解
定义无量纲参数起始比降因子R=i0H/Δh。显然,若i0越大,Δh越小,则R越大,渗流越难以到达土层顶部。该问题可分为2种情况。
1) 当R>1时,渗流逐渐向土层顶部发展但不能发展到土层顶部,此时,渗流最终边界至基准面的距离为Hc=(1-1/R)H,在该边界以上土体不会发生固结。由于边界条件非齐次,因此,采用变量替换的方法将原问题化为齐次边界问题,引入变量w,变换为
 (7)
(7)
则原问题的固结方程和求解条件变为:
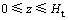 ,
, (8)
(8)
 ,
, (9)
(9)
初始条件:
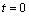 ,
, (10)
(10)
边界条件:
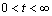 ,
,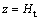 ,
,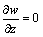 (11)
(11)
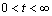 ,
,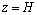 ,
,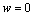 (12)
(12)
采用分离变量法可得式(9)的解为
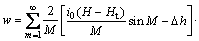
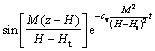 (13)
(13)
式中: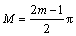 ;
; 。
。
式(13)应在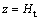 处满足式(8),即
处满足式(8),即
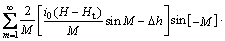
 (14)
(14)
联合R=i0H/Δh,可将式(14)整理为
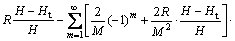
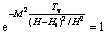 (15)
(15)
式中:Tv为竖向固结时间因子,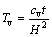 。对应特定的R可从上式获得时间t(或时间因子Tv)与渗流移动边界至基准面距离Ht之间的对应关系。
。对应特定的R可从上式获得时间t(或时间因子Tv)与渗流移动边界至基准面距离Ht之间的对应关系。
弱透水层中任一时刻任一深度处的水头为
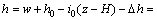
 (16)
(16)
弱透水层中任一时刻任一深度处的孔压为
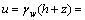
 (17)
(17)
式中: 为水的重度。
为水的重度。
则任意t时刻弱透水层的压缩量S ct为
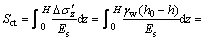
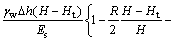
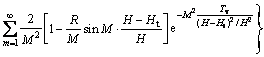 (18)
(18)
式中:Es为弱透水层的压缩模量;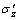 为某深度处有效应力改变量;S ct为任意时刻弱透水土层的压缩量,当时间趋于无穷大时,压缩量
为某深度处有效应力改变量;S ct为任意时刻弱透水土层的压缩量,当时间趋于无穷大时,压缩量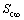 为
为
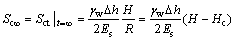 (19)
(19)
其中: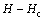 为发生固结的土层厚度。
为发生固结的土层厚度。
按沉降定义的地基平均固结度Us为

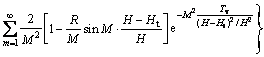 (20)
(20)
2) 当0<R≤1时,渗流逐渐向土层顶部发展且能够发展到达土层顶部,此时渗流的最终边界即为基准面,或即Hc=0,整个弱透水层均将会发生固结。在渗流到达土层顶部前,以水头表示的一维固结微分方程和求解条件与R>1时渗流不能到达土层顶部时相同。可设渗流刚好到达土层顶部时历时t0,则由式(15)可得
 (21)
(21)
对应特定的R(0<R≤1),可得渗流发展到达土层顶部时的时间因子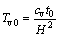 。
。
此时弱透水层任一深度处水头为
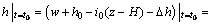
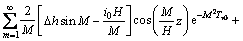
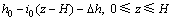 (22)
(22)
当渗流到达顶部后,定解模型为
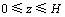 ,
, (23)
(23)
求解条件如下。
初始条件 ,
,

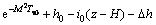 (24)
(24)
边界条件:
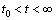 ,
,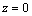 ,
,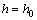 (25)
(25)
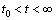 ,
,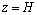 ,
,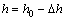 (26)
(26)
同理引入变换
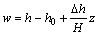 (27)
(27)
同理可得
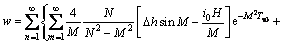
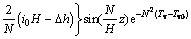 (28)
(28)
式中: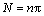 ;
; 。
。
当弱透水层t≥t0时,任一时刻任一深度的水头为
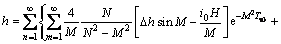
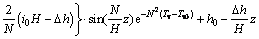 (29)
(29)
当弱透水层t≥t0时,任一时刻任一深度的孔压为
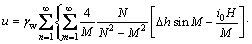
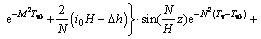
 (30)
(30)
a) 当t<t0时,渗流移动边界未发展到达土层顶部,固结压缩量可按渗流不能发展到达土层顶部情况下的压缩量(式(18))计算;
b) 当t≥t0时,
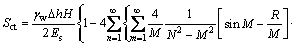
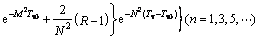 (31)
(31)
当时间趋于无穷大时,压缩量为
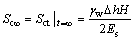 (32)
(32)
按沉降定义的地基平均固结度为
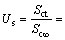
 (33)
(33)
当起始比降i0=0时,可得R=i0H/Δh=0,继而Tv0=0,t0=0,水位下降后渗流瞬间发展到达土层顶部,按沉降定义的平均固结度退化为

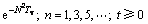 (34)
(34)
其计算值与骆冠勇等[4]获得的解析解计算结果相同,验证了本文解的合理性。
此外,若研究考虑起始比降水位下降引起的下卧弱透水层固结问题,此时,由于存在对称性,只需建立向上的坐标系,基准面取在弱透水层底面,则求解结果完全相同。
3 土层固结分析
3.1 渗流移动边界
据式(15)可得图2所示的不同起始比降下渗流移动边界随时间的运动曲线。由图2可见:与太沙基一维固结理论不同,由于起始比降的存在,渗流并不会瞬间在整个土层发生。当下层主含水层水位下降后,渗流移动边界随时间推移逐渐向土层顶部移动。当起始比降较小时,渗流能够很快发展到达土层顶部,随着起始比降增大,渗流发展到达土层顶部的时间越长。当土层起始比降大于一定值(R>1)时,渗流移动边界运动至某一深度,便停止向上移动,并不会发展到达土层顶部。在该深度以上土层,并不会发生固结,且起始比降越大,发生固结土层的厚度越小。图3所示为渗流发展到土层顶部时间因子与起始比降的关系曲线。由图3可看出:随着起始比降R的增大,渗流发展到达土层顶部的时间因子越大,当R>1时,渗流发展到达土层顶部的时间因子趋于无穷大,即渗流不能到达土层顶部。综上所述,起始比降阻碍了渗流的发展。
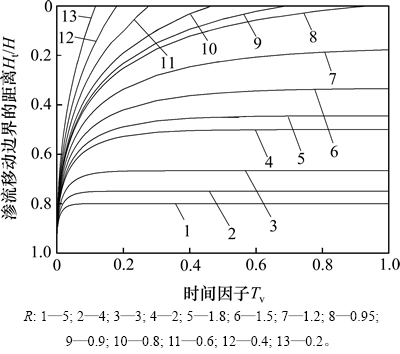
图2 渗流移动边界的运动
Fig. 2 Motion of moving boundary of seepage

图3 渗流发展到土层顶部时间因子与起始比降的关系曲线
Fig. 3 Curve of time moving boundary of seepage takes to reach top of layer versus threshold gradient
3.2 沉降曲线
不同起始比降下土层固结压缩量随时间发展曲线如图4所示,其中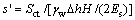 。由图4可知:起始比降R越大,到达相同压缩量所需时间越长,相同时间因子下压缩量越小。当起始比降较小时(0<R≤1)时,渗流能够到达土层顶部,其最终压缩量均为一定值,
。由图4可知:起始比降R越大,到达相同压缩量所需时间越长,相同时间因子下压缩量越小。当起始比降较小时(0<R≤1)时,渗流能够到达土层顶部,其最终压缩量均为一定值,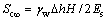 ;当起始比降达到一定值时(R>1),将影响渗流发展的深度,使发生固结的土层厚度减小,其最终压缩量将变小,
;当起始比降达到一定值时(R>1),将影响渗流发展的深度,使发生固结的土层厚度减小,其最终压缩量将变小,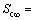
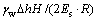 ,可知其值与R相关,R越大,最终压缩量越小。当R=0时,即不考虑起始比降时,渗流能瞬时到达土层顶部,其最终压缩量与0<R≤1时的压缩量相同,且相同时间因子下压缩量最大,与太沙基双面排水条件下一维固结解相等。
,可知其值与R相关,R越大,最终压缩量越小。当R=0时,即不考虑起始比降时,渗流能瞬时到达土层顶部,其最终压缩量与0<R≤1时的压缩量相同,且相同时间因子下压缩量最大,与太沙基双面排水条件下一维固结解相等。
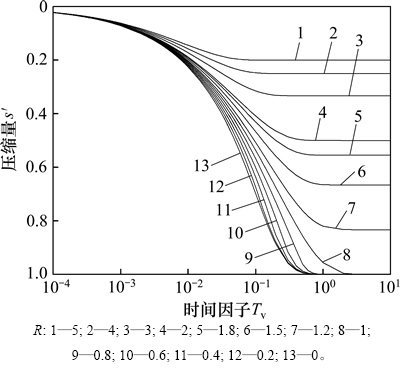
图4 不同起始比降下压缩量与时间因子曲线
Fig. 4 Compression versus time curves with different threshold gradients
3.3 孔隙水压力的分布
当主含水层水位下降后,随着时间的发展,弱透水层中水头逐渐降低,孔隙水压力逐渐减小,有效应力逐渐增加。分别取时间因子Tv=0.1时和土体固结完成时2种情况,计算不同起始比降下水头、孔压沿深度分布曲线,如图5~8所示,其中H=10 m,h0=10 m,△h= 5 m。由图5~8可知:起始比降越大,水头下降越慢,孔压减小得也越慢;当起始比降达到一定值时 (R>1),渗流并不会发展到达土层顶部,此时,最终渗流边界上部的土层将不会发生固结,在固结结束时水头和孔隙水压力仍将保持不变,水头和孔隙水压力沿深度的分布曲线均为折线;当起始比降较小时(0<R≤1),渗流最终能够发展至土层顶部,整个土层均发生固结。当固结结束时,水头和孔隙水压力沿深度的分布曲线均为直线。

图5 Tv=0.1时不同起始比降下水头沿深度变化曲线
Fig. 5 Water head versus depth curves with different threshold gradients at Tv=0.1
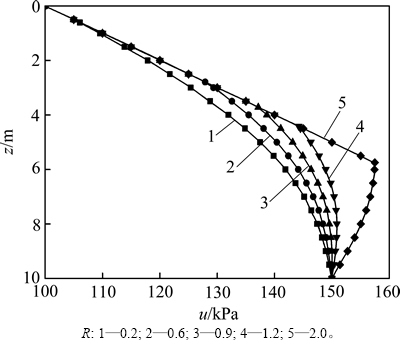
图6 Tv=0.1时不同起始比降下孔压沿深度变化曲线
Fig. 6 Pore water pressure versus depth curves with different threshold gradients at Tv=0.1
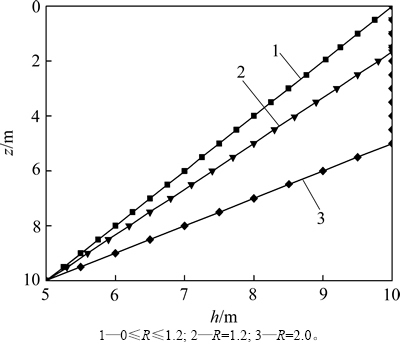
图7 固结结束时不同起始比降下水头沿深度变化曲线
Fig. 7 Water head versus depth curves with different threshold gradients at the end of consolidation
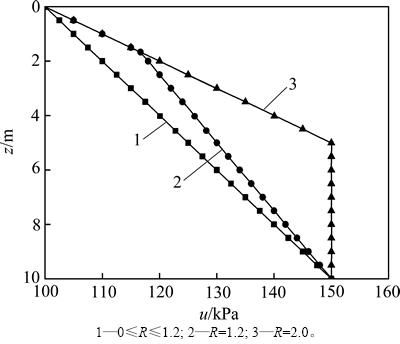
图8 固结结束时不同起始比降下孔压沿深度变化曲线
Fig. 8 Pore water pressure versus depth curves with different threshold gradients at the end of consolidation
4 结论
1) 分析了考虑起始比降下水位下降引起的一维固结问题,并获得了不同起始比降下相应的一维固结解答。当起始比降i0=0时,本文退化解与解析解计算结果相同,表明本文解答是合理的。
2) 与起始比降为0时渗流瞬间在整个土层发生不同,当存在起始比降时,土中渗流是逐渐向上发展的。起始比降越大,渗流边界在土中的移动速度越慢。当起始比降在一定范围内时(0<R≤1),渗流均能在一定时间发展到达土层顶部,且最终压缩量相同;当起始比降大于一定值时(R>1),土中渗流虽能逐渐向上发展,但是并不会发展到达土层顶部,且起始比降越大,发生固结的土层厚度越小,最终压缩量越小。
3) 起始比降越大,降水后土中水头下降越慢,孔压减小得也越慢。当渗流能够发展到达土层顶部时,固结结束时,水头和孔隙水压力沿深度的分布曲线均为直线;当渗流不能发展到达土层顶部时,固结结束时,水头和孔隙水压力沿深度的分布曲线均为折线。
参考文献:
[1] CHEN Chongxi, PEI Shunping, JIAO Jiu. Land subsidence caused by groundwater exploitation in Suzhou City, China[J]. Hydrogeology Journal, 2003, 11(2): 275-287.
[2] CHAI J C, SHEN S L, ZHU H H, et al. Land subsidence due to groundwater drawdown in Shanghai[J]. Geotechnique, 2004, 54(2): 143-147.
[3] XUE Yuqun, ZHANG Yun, YE Shujun, et al. Land subsidence in China[J]. Environmental Geology, 2005, 48(6): 713-720.
[4] 骆冠勇, 潘泓, 曹洪, 等. 承压水减压引起的沉降分析[J]. 岩土力学, 2004, 25(11): 196-200.
LUO Guanyong, PAN Hong, CAO Hong, et al. Analysis of settlements caused by decompression of confined water[J]. Rock and Soil Mechanics, 2004, 25(11): 196-200.
[5] TSENG C M, TSAI T L, HUANG L H. Effects of body force on transient poroelastic consolidation due to groundwater pumping[J]. Environmental Geology, 2008, 54(7): 1507-1516.
[6] TSAI T L. Viscosity effect on consolidation of poroelastic soil due to groundwater table depression[J]. Environmental Geology, 2009, 57(5): 1055-1064.
[7] SHEN Shuilong, XU Yeshuang. Numerical evaluation of land subsidence induced by groundwater pumping in Shanghai[J]. Canadian Geotechnical Journal, 2011, 48(9): 1378-1392.
[8] LIU Jiacai, LEI Guogang, MEI Guoxiong. One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater[J]. Journal of Central South University, 2012, 19(1): 282-286.
[9] 谢康和, 陶立为, 王玉林, 等. 越流系统中弱透水层的一维固结解及分析[J]. 沈阳工业大学学报, 2012, 34(5): 581-585.
XIE Kanghe, TAO Liwei, WANG Yulin, et al. One-dimensional consolidation solution and analysis for aquitard in leakage system[J]. Journal of Shenyang University of Technology, 2012, 34(5): 581-585.
[10] MILLER R J, LOW P F. Threshold gradient for water flow in clay systems[J]. Soil Science Society of America Journal, 1963, 27(6): 605-609.
[11] MITCHELL J K, YOUNGER J S. Abnormalities in hydraulic flow through fine-grained soils[M]. Philadelphia: ASTM International, ASTM Special Publication, 1967: 106-141.
[12] 刘慈群. 有起始比降固结问题的近似解[J]. 岩土工程学报, 1982, 4(3): 107-109.
LIU Ciqun. Approximate solution for one-dimensional consolidation with threshold gradient[J]. Chinese Journal of Geotechnical Engineering, 1982, 4(3): 107-109.
[13] 邓英尔, 刘慈群, 王允诚. 一类非线性渗流数学模拟[J].云南石油学院学报, 2001, 23(1): 22-24.
DENG Yinger, LIU Ciqun, WANG Yuncheng. Mathematical simulation for a class of nonlinear flow[J]. Journal of Yunnan Petroleum Institute, 2001, 23(1): 22-24.
[14] 刘忠玉, 刘忠广, 马崇武. 考虑起始水力梯度时饱和黏土的一维固结[J]. 郑州大学学报, 2006, 27(3): 21-24.
LIU Zhongyu, LIU Zhongguang, MA Chongwu. One dimensional consolidation of saturated clays considering initial hydraulic gradient[J]. Journal of Zhengzhou University, 2006, 27(3): 21-24.
[15] XIE Kanghe, WANG Kun, WANG Yulin, et al. Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient[J]. Computers and Geotechnics, 2010, 37(6): 487-493.
[16] 王坤, 谢康和, 刘兴旺, 等. 初始孔压非均布考虑起始比降的一维固结解[J]. 岩土工程学报, 2011, 33(9): 1419-1424.
WANG Kun, XIE Kanghe, LIU Xingwang, et al. Solution for one-dimensional consolidation with threshold gradient subjected to non-uniformly distributed initial pore water pressure[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1419-1424.
[17] 黄杰卿, 谢新宇, 王文军, 等. 考虑起始比降的饱和土体一维复杂非线性固结研究[J]. 岩土工程学报, 2013, 35(2): 355-363.
HUANG Jieqing, XIE Xinyu, WANG Wenjun, et al. Study on one-dimensional nonlinear consolidation behavior for saturated soils with threshold gradient[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 355-363.
[18] 周煜, 谢康和, 刘兴旺. 考虑起始比降和涂抹作用的竖井地基固结解[J]. 工程力学, 2014, 31(2): 103-109.
ZHOU Yu, XIE Kanghe, LIU Xingwang. Analytical solution for vertical drains considering threshold gradient and smear effect[J]. Engineering Mechanics, 2014, 31(2): 103-109.
(编辑 刘锦伟)
收稿日期:2015-03-25;修回日期:2015-05-10
基金项目(Foundation item):国家自然科学基金资助项目(51278453,51179170);国家教育部博士点基金资助项目(20120101110029) (Projects (51278453, 51179170) supported by the National Natural Science Foundation of China;Project(20120101110029) supported by the Research Fund for the Doctoral Program of Higher Education of China)
通信作者:谢康和,博士,教授,博士生导师,从事岩土工程方面的教学和科研;E-mail: zdkhxie@zju.edu.cn