J. Cent. South Univ. Technol. (2010) 17: 419-424

DOI: 10.1007/s11771-010-0062-y                                                                                                                   

Integrated reliability of travel time and capacity of urban road network under ice and snowfall conditions

LENG Jun-qiang(冷军强)^{1, 2}, ZHANG Ya-ping(张亚平)¹, ZHANG Qian(张倩)², ZHAO Ying-ping(赵莹萍)²

1. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China;

2. School of Automobile Engineering, Harbin Institute of Technology, Weihai 264209, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: In order to evaluate and integrate travel time reliability and capacity reliability of a road network subjected to ice and snowfall conditions, the conceptions of travel time reliability and capacity reliability were defined under special conditions. The link travel time model (ice and snowfall based-bureau public road, ISB-BPR) and the path choice decision model (elastic demand user equilibrium, EDUE) were proposed. The integrated reliability was defined and the model was set up. Monte Carlo simulation was used to calculate the model and a numerical example was provided to demonstrate the application of the model and efficiency of the solution algorithm. The results show that the intensity of ice and snowfall, the traffic demand and supply, and the requirements for level of service (LOS) have great influence on the reliability of a road network. For example, the reliability drops from 65% to 5% when the traffic demand increases by 30%. The comprehensive performance index may be used for network planning, design and maintenance.

Key words: integrated reliability; urban road network; travel time; capacity; Monte Carlo simulation; bi-level program; ice and snowfall

1 Introduction

The reliability is a measure of road network to resist traffic uncertainties. This issue has gradually become a major concern for many scholars [1-4]. At present, the network reliability researches are focused on network connection reliability, travel time reliability and capacity reliability [5-7]. The travel time reliability is the probability of which a trip between a given origin destination (OD) pair can be made successfully within a specified interval of time for a given level of traffic demand [8-9]. It was originally proposed by ASAKURA and KASHIWADANI [10] in 1991 to investigate the impact of OD demand level fluctuation on travel time. In 2005, CLARK and WALTING [11] proposed the model of network travel time reliability under stochastic demand. Capacity reliability is the probability of which the network can accommodate a certain traffic demand at a required level of service (LOS). It was proposed by CHEN et al [6]. In 2002, CHEN et al [12] developed a evaluation framework of capacity reliability, which combined reliability, uncertainty analysis, user equilibrium models, sensitivity analysis and Monte Carlo simulation. In 2006, DEEK and EMAM [13] proposed a new methodology for estimating reliability in transportation networks with degraded link capacity. In 2008, WILLIAM et al [14] developed a model of impacts of adverse weather conditions on a road network with uncertainties in demand and supply. XIONG et al  [1] developed an integrated method for road network reliability under stochastic demand. KUANG et al [15] performed an analysis on road network capacity reliability based on OD pair travel time reliability.

The reliability researches, as mentioned above, are all very useful and important. Imperfectly, there are two major limitations. On the one hand, there is no comprehensive performance index, since most of the focuses are limited to one single performance estimation index. On the other hand, the reliability mainly focuses on day-to-day recurrent traffic congestion. There are very few researches on adverse weather conditions, except WILLIAM et al [14] studied the network reliability under the adverse weather conditions of rain.

Consequently, one objective of this work is to explore the road network reliability under ice and snowfall conditions. The other is to synthesize the reliabilities of travel time and capacity as a compre- hensive index that can well reflect the overall network reliability with supply and demand uncertainties.

2 Travel time reliability under ice and snow- fall conditions

2.1 Travel time reliability

Taking into account the influence of adverse weather, the travelers’ requirements for travel time will correspondingly decrease, so will the demand for lower LOS. The average travel time under normal weather may be used as expected travel time of travelers. Under the assumption that road network is reliable under normal conditions (without ice and snowfall influence), travel time reliability is defined as the probability of which actual travel time is not (1+δ) times longer than the mean travel time, where δ is an acceptable proportion of travel time increase, and is different for each link, which may be calibrated by the field observation. The definition formula can be expressed as

R=P[t≤(1+δ)E₀(t₀)]                           (1)

where R is the travel time reliability; P[?] is the probability of which actual travel time is not (1+δ) times longer than the mean travel time; t is the actual travel time under ice and snowfall conditions; and E₀(t₀) is the average travel time under normal weather conditions.

2.2 Link travel time function

In previous researches, the conventional bureau public road (BPR) model was widely used in the estimation of travel time reliability. With the influence of ice and snowfall, visibility and pavement friction will decrease. As a result, there is a great deal of reduction in traffic performance parameters (e.g., longer travel time, lower free-flow speed and link capacity). Therefore, the BPR model is not applicable directly to the adverse weather conditions. To calibrate and capture the actual functional relationship between the adverse impacts and link travel time, a new model of link travel time was set up based on BPR model, named as ice and snowfall based-bureau of public road (ISB-BPR) model. It can be written as

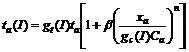               (2)

where t_a(I) is the actual travel time on link a with the influence of ice and snowfall; I is the intensity of ice and snowfall; t_a is the free-flow travel time on link a; g_t(I) and g_c(I), respectively, denote the influence of ice and snowfall on travel time and capacity, which are the functions of ice and snowfall intensity; x_a and C_a, respectively, are the traffic demand and capacity on link a; and β and n are parameters.

3 Capacity reliability under ice and snowfall conditions

3.1 Capacity reliability

Road network capacity reliability is the probability of which road network can accommodate a certain traffic volume at an acceptable LOS. At present, there is no recognized definition. CHEN [6, 12] proposed a classical one based on the reserve capacity μ. Considering the capacity variation, μ was treated as a random variable. It was defined as the largest multiplier applied to a given existing OD demand that can be allocated to a road network without surpassing the link capacity. Therefore, μ was subjected to the link flows resulting from the network equilibrium problem not exceeding the link capacity. However, it cannot fully take into account different requirements for LOS. In this work, the capacity reliability is the probability of which actual traffic volume level μ_r is not ε times larger than the reserve capacity μ. It may be expressed as follows:

R(μ_r)=P(μ_r≤εμ)                              (3)

where ε denotes different requirements for link or path LOS, 0＜ε≤1. The smaller the ε, the higher the LOS requirement, the lower the reliability.

3.2 Capacity bi-level program model

The reserve capacity μ is subjected to the link flows resulting from the network equilibrium problem [12]. The maximum capacity problem can be expressed as a bi-level program as follows:

The upper level: μ=max μ                   (4)

s.t.  x_a(μ)≤C_a,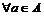

where x_a(μ) is the equilibrium flow on link a with reserve capacity μ; and A is the collection of links. Besides traffic supply and demand, the path choice decision has a great influence on network capacity. At present, with the accuracy of weather forecast and the perfection of information induction system, the travelers may choose their routes and change travel mode, even cancel their trip under the adverse weather. Based on the above consideration, the elastic demand user equilibrium (EDUE) model was proposed. Mathematically, the relationship between traffic volume and travel time of OD pair (s, t) can be written as:

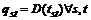                                  (5)

where q_s,t and t_s,t are the traffic volume and the travel time between OD pair (s, t), respectively; and D_st(?) is the traffic demand function of OD pair (s, t).

This is an equilibrium allocation of variable traffic demand, which may be served as a lower level program, from which link and OD traffic volume can be obtained, meeting the balance principle of Wardrop. Mathematically, it can be formulated as follows.

The lower level:

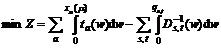          (6)

s.t. 

≥

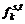q_s,t≥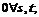

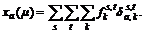
where 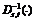 is the inverse function of D_s,t(?);  is the flow on path k between OD pair (s, t); 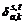 is a 0-1 variable, if link a belongs to path k of OD pair (s, t), then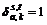; otherwise, .

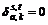To facilitate the application of path choice model, detailed steps of the procedure are described as follows.

Step 1: Initialize. Let n=1 and find the initial feasible link traffic volume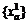and OD traffic volume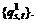

Step 2: Update travel time. Let  calculate.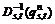

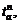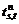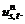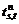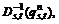Step 3: According to  find the shortest route between the OD pair (s, t), decide the iteration direction, and calculate travel time  of the shortest route between OD pair (s, t). Then, according to the following formula, calculate the additional traffic flow  If  ≤ let 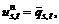 where  is the upper limit of traffic between OD pair (s, t). 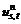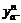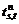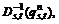Moreover, do 0-1 allocation on the shortest route, namely, allocate traffic volume  on the shortest route and add the corresponding additional link traffic flow If ＞ let 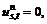and the corresponding additional link traffic flow  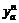will be no more changeable, and additional traffic volume  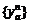and OD traffic  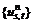can be obtained.

Step 4: Calculate optimal step length by solving the following 1-dimensional minimal question:

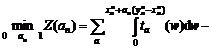
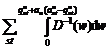
Step 5: Update traffic volume:   

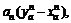
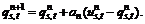
Step 6: Test convergence:

≤

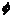
where 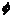 is the pre-set criterion of error. If the above formula is valid, then stop; otherwise, let n=n+1 and return to step 2.

4 Integrated reliability of travel time and capacity

4.1 Model establishment

The reliabilities, as mentioned above, are very important measure indexes of road network. Unfortunately, there is a major drawback that the travel time and capacity reliabilities are highly correlated. However, few researchers have attached great efforts on the comprehensive estimation of the travel time and capacity reliabilities. Consequently, in this work, we made efforts to join the above two types of reliabilities, and established the joint probability distribution model under ice and snowfall conditions, which can more comprehensively estimate the performance of the stochastic road network and provide a more reasonable calculation method.

The integrated reliability of travel time and capacity is defined as follows. It is the probability of which the actual travel time is not (1+δ) times longer than the average travel time under normal weather and the actual traffic volume level μ_r is not ε times larger than the reserve capacity μ. Then the formula may be expressed as

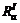=P(t′_a(I)≤(1+δ)E₀(t_0a), μ_r≤εμ)               (7)

where 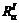 denotes the integrated reliability of link a; t′_a is the actual travel time on link a under ice and snowfall conditions; E₀(t_0a) is the average travel time on link a under normal weather conditions. It should be noted that if δ→∞ (the travel time reliability can be omitted), the formula may be simplified as the capacity reliability. If  ε→∞ (the capacity reliability can be omitted), the formula can be simplified as the travel time reliability mentioned above.

With the integrated reliability of links, the integrated reliabilities of path and OD pair can be easily concluded. The path integrated reliability can be expressed as

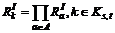                          (8)

where 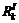 is the integrated reliability of path k between OD pair (s, t); and K_s,t is the collection of paths between OD pair (s, t). If there are m paths between OD pair (s, t), the integrated reliability of OD pair (s, t),  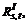can be expressed as

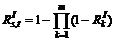                          (9)

4.2 Monte Carlo simulation

In this work, link capacity C_a and traffic volume q_s,t are both random variables. Due to the absence of observed field data, it is assumed that they follow the normal distributions. Here, the random variable generator (RVG) was used to generate the distributions. The flow chart of algorithm is shown in Fig.1.

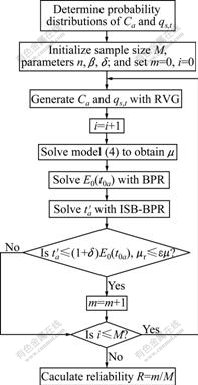
Fig.1 Flow chart of algorithm of Monte Carlo simulation

5 Numerical example

5.1 Simulation settings

A simple test road network is used to demonstrate the performance of the proposed model and algorithm. This network consists of four zones, six nodes and eight links, as shown in Fig.2, where zones 1-2 are trip origin zones and zones 5-6 are destination ones. The link data are shown in Table 1. The forecast levels of hourly average snowfall intensity are as follows: light snowfall (≤2.4 cm/d), normal snowfall (≤4.9 cm/d), amber snowfall (≤9.9 cm/d) and red snowfall (≥10.0 cm/d). Therefore, ice and snowfall intensity may be assumed as depth of snowfall. The base traffic demand OD is given in passenger car unit per minute (pcu/min), as shown in Table 2. The link travel time is calculated from the ISB- BPR formula, where β=0.15, n=4.

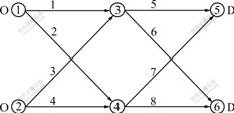
Fig.2 Schematic diagram of test road network

Table 1 Link data of test road network

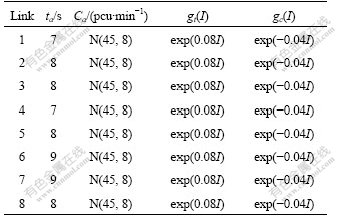
Table 2 Distributions of base traffic demand

5.2 Simulation results and analysis

In the simulation, capacity degradation of each link is independent and random variables C_a and q_st are assumed as normal distributions. The estimated means and standard deviations of random variables resulting from 4 000 simulations are very close to the theoretical values. The deviation is less than 1%.

To illustrate the effect of the snowfall intensity on the reliability, four scenarios of OD pair (2, 5) under different snowfall intensities are simulated and the results are shown in Fig.3. Fig.3 shows that the reliability drops steeply with the increase of snowfall intensity. This is in accordance with the fact that the visibility and pavement friction decrease with increasing influence of ice and snowfall conditions.

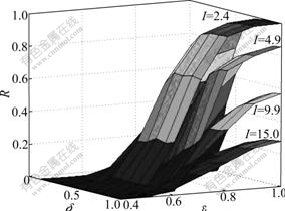
Fig.3 Effect of snowfall intensity on integrated reliability

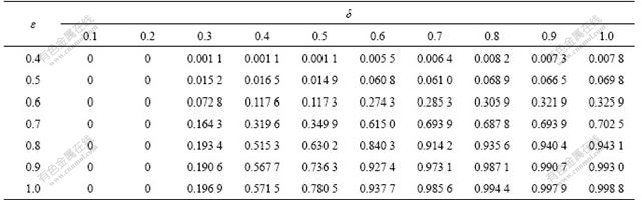
To illustrate the effect of different LOS requirements on the reliability, the following scenarios are simulated. For simplification, set particular snowfall intensity I=2.4. Table 3 lists the integrated reliability of link 1 at different LOS. Table 4 lists the integrated reliability of OD pair (1, 5). Due to the limitation of paper pages, only parts of tables are listed here. The data are rationally distributed as expected. With the decrease of saturation requirements (ε increases), the reliability becomes higher. Similarly, with the decrease of LOS requirements for travel time (δ increases), the reliability also becomes higher. On the other hand, higher LOS requirements result in lower reliability.

Table 3 Integrated reliability of link 1 at different LOS

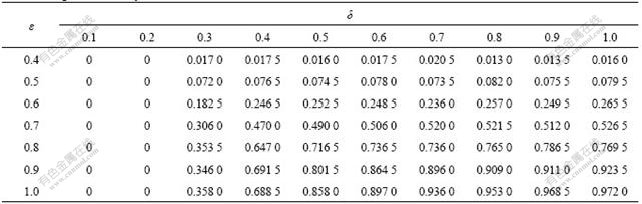
Table 4 Integrated reliability of OD pair (1, 5) at different LOS

The influence of traffic demand fluctuation and capacity degradation on reliability was studied. When particular saturation requirement ε is 0.8, traffic demand levels are 100%, 110%, 120% and 130%, and capacity degradations are 0.4, 0.6, 0.8 and 1.0, the simulation results of OD pair (1, 6) are shown in Figs.4 and 5, respectively. From the two figures, it can be seen that both traffic demand fluctuation and link capacity degradation are important factors in reliability analysis. The road network is frangible, and minor fluctuation may cause deterioration of traffic situation.

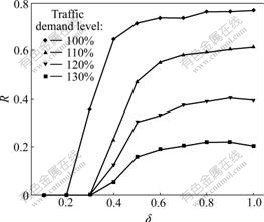
Fig.4 Integrated reliability under different traffic demands

  Fig.5 Integrated reliability under different traffic capacity degradations

6 Conclusions

(1) The traffic demand, supply and intensity of ice and snowfall have obvious influence on the integrated reliability of a road network, and the road network is more sensitive under ice and snowfall conditions. For example, the integrated reliability drops from 90% to 0 when the traffic supply is 40% of the capacity. The reliability and requirements for LOS are closely correlated together. Moreover, the same road network has different reliabilities at different LOS. In addition, the higher the LOS, the lower the road network reliability.

(2) Only a small size road network is tested and normal probability distributions are adopted. But the method has true potential and can be extended to large-scale network and other adverse weather conditions. Next step, the ISB-BPR function, traffic demand and supply functions should be calibrated and the best-fit distributions should be developed by using actual observed field data. Besides the ice and snowfall conditions, the function of link travel time can be extended to other adverse weather conditions, e.g. fog and rainfall conditions.

References

[1] XIONG Zhi-hua, SHAO Chun-fu, YAO Zhi-sheng. Integrated method for road network reliability under stochastic demand [C]// Proceedings of the Conference on Traffic and Transportation Studies. Restone: American Society of Civil Engineers, 2006: 425-434.

[2] BELL M G H. A game theory approach to measuring the performance reliability of transport networks [J]. Transportation Research (Part B): Methodological, 2000, 34(6): 533-545.

[3] DIMITRIOU L, STATHOPOULOS A, TSEKERIS T. Reliable stochastic design of road network systems [J]. International Journal of Industrial and Systems Engineering, 2008, 3(5): 549-574.

[4] HU S, WILLIAM L, MEI T. A reliability-based stochastic traffic assignment model for network with multiple user classes under uncertainty in demand [J]. Networks and Spatial Economics, 2006, 6(3): 173-204.

[5] LENG Jun-qiang, ZHANG Ya-ping, LENG Yu-quan. Assessment of road network capacity reliability based on the constraints of link LOS [J]. Journal of Transportation Systems Engineering and Information Technology, 2009, 9(5): 148-152. (in Chinese)

[6] CHEN A, TATNENI M, LEE D H, YANG H. Effect of route choice models on estimating network capacity reliability [J]. Transportation Research Record, 2000(1733): 63-70.

[7] ASAKURA Y. Requirements for transport network flow models used in reliability analysis [J]. International Journal of Critical Infrastructures, 2007, 3(3/4): 287-300.

[8] LO H K, LUO X W, SIU B W Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion [J]. Transportation Research (Part B): Methodological, 2006, 40: 792- 806.

[9] UNO N, KURAUCHI F, TAMURA H, IIDA Y. Using bus probe data for analysis of travel time variability [J]. Journal of Intelligent Transportation Systems: Technology, Planning and Operations, 2009, 13(1): 2-15.

[10] ASAKURA Y, KASHIWADANI M. Road network reliability caused by daily fluctuation of traffic flow [C]// Proceedings of the 19th PTRC Summer Annual Conference. Brighton: Seminar G, 1991: 73-84.

[11] CLARK S, WALTING D. Modeling network travel time reliability under stochastic demand [J]. Transportation Research (Part B): Methodological, 2005, 39(12): 119-140.

[12] CHEN A, YANG H, LO H K, TANG W H. Capacity reliability of a road network: An assessment methodology and numerical results [J]. Transportation Research (Part B): Methodological, 2002, 36(3): 225- 252.

[13] DEEK A H, EMAM E B. New methodology for estimating reliability in transportation networks with degraded link capacities [J]. Journal of Intelligent Transportation Systems: Technology, Planning and Operations, 2006, 10(3): 117-129.

[14] WILLIAM H K L, HU S, AGACHAI S. Modeling impacts of adverse weather conditions on a road network with uncertainties in demand and supply [J]. Transportation Research (Part B): Methodological, 2008, 42(10): 890-910.

[15] KUANG A W, HUANG Z X, CHAN W K V. An analysis on road network capacity reliability based on OD pair travel time reliability [C]// Proceedings of International Conference on Intelligent Computation Technology and Automation. Piscataway: Institute of Electric and electronic Engineering Computer Society, 2008: 333-337.

Foundation item: Project(E200940) supported by the Natural Science Foundation of Heilongjiang Province, China; Project(2009GC20008020) supported by the Technology Research and Development Program of Shandong Province, China

Received date: 2009-06-07; Accepted date: 2009-11-30

Corresponding author: ZHANG Ya-ping, Professor; Tel: +86-451-86282966; E-mail: zxlt0905@163.com

(Edited by CHEN Wei-ping)