J. Cent. South Univ. Technol. (2008) 15(s1): 568-572

DOI: 10.1007/s11771-008-423-y

Thermomechanical coupling effect of PVC sheet with defects

YANG Zhan-yu(杨占宇)¹, LUO Ying-she(罗迎社)¹, SU Jian-xin(粟建新)²,

ZHANG Yong-zhong(张永忠)³, DENG Xu-hua(邓旭华)⁴, CHEN Sheng-ming(陈胜铭)¹,

DENG Rui-ji(邓瑞基)¹, MA Min-wei(马敏伟)¹, ZHANG Liang(张 亮)¹

(1. Institute of Rheological Mechanics and Material Engineering,

Central South University of Forestry and Technology, Changsha 410004, China;

2. College of Information Engineering, Xiangtan University, Xiangtan 411105, China;

3. College of Electronic and Information Engineering,

Central South University of Forestry and Technology, Changsha 410004, China;

4. Institute of Fundmental Mechanics and Material Engineering, Xiangtan University, Xiangtan 411105, China)

Abstract: Thermomechanical coupling of PVC sheet with defects under uniaxial loading at different rates and different sizes of microbores was studied. The local temperature field of the dynamic damage-rupture process zone at crack tip was surveyed with infrared thermographic sensor. Based on the irreversible thermomechanics theory, the dissipation law of deformation-heat effect during the whole process was found. Furthermore, the effect of thermoelasticity in the initial stage of extension was explained.

Key words: thermomechanical coupling; irreversible thermomechanics; dissipation; thermoelasticity effect

1 Introduction

High polymer materials have inevitably different kinds of micro-defects (such as microbores, inclusions, micro-crack, etc), which could lead to degradation or failure of macroscopic mechanical function during the use of these materials. The evolution of defect implies the damage and deformation of material, and accompanies with various energy forms of conversions during this process. Furthermore, this process is not a pure mechanical process. Essentially, it relates to the coupling problems including various physical fields (force, heat, electricity, magnetism, light, voice). It is obviously difficult to study those complex nonlinear relations among external fields.

The thermo-sensitive area of high polymer material is in the scope of several dozens degree higher or lower than room temperature, which means that we must consider the impact of changes in temperature in the use of high polymer material. The deformation of material leads to temperature gradient, and causes the conduction and dissipation of heat. Therefore, the system is in the nonequilibrium state. In this work, based on the theory of nonequilibrium thermomechanics and rheological- thermomechanics, the thermomechanical coupling effect of high polymer material under loading at normal temperature was studied

2 System of thermomechanical coupling

2.1Theory frame of nonequilibrium thermomechanics

Energy conservation:

dU=Q+W                                   (1)

Entropy equation:

dS=d_iS+d_eS, d_iS≥0                            (2)

Linear law of forces and fluxes:

J=LX                                      (3)

Phenomenological relation:

J_i=∑L_ijX_i                                    (4)

Onsager’s reciprocity relation:

L_ik=L_ki                                      (5)

Entropy production:

σ= ∑XJ                                     (6)

where  U, Q, W, dS, d_iS, d_eS, J, X, L and σ stand for the change of internal energy, heat, work, change of entropy, production of entropy, transport of entropy, thermo-

mechanical flux, thermomechanical force, phenomeno- logical coefficient and entropy production, respectively.

2.2 Linear nonequilibrium

In the linear zone of nonequilibrium, relationships between thermomechanical forces and fluxes meet the phenomenological relation and Onsager’s reciprocity relation, so the internal variable and local equilibrium assumption can be introduced to discuss the energy dissipation law of material under tension^[1]. Therefore, entropy production rate equation shown in Eqn.(9) can be obtained based on the energy conservation law shown in Eqn.(7) and Gibbs equation shown in Eqn.(8).

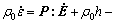div₀q₀                     (7)

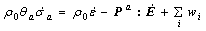            (8)

where   the right side of equation means summation.

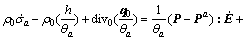
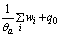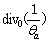?                     (9)

The right part of Eqn.(9) can be considered the point multiplication of generalized thermomechanical forces

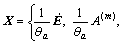div₀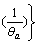

and generalized thermomechanical fluxes J={(P-P^a), 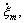q₀}; ξ_m describes the internal variable of nonequilibrium dissipation process inside the material; A^(m) means the generalized internal force, here, m=1, 2, …; P-P^a is equal to viscous stress P^v; a, ρ_o, ε, P, E, h, q₀, θ and σ stand for constrained equilibrium state, the quality density of the initial reference structure of material, the internal energy density, stress tensor, strain tensor, distribution heat source per unit time and unit quality, the heat flux vector of the initial reference structure on the surface of material, the absolute temperature and entropy, respectively; stands for the irreversible dissipative rate caused by various internal variables.

In the failure process of high polymer material, the process zone at crack tip experiences a large nonlinear deformation from elastic deformation to elastic-plastic deformation, then forms elastic-viscoplastic deformation at last^[2]. The material can be considered thermoelastic body at the initial process of tension, P^v and A^(m) both are equal to 0, and the thermomechanics state function is used to obtain the corresponding heat transfer Eqn.(10):

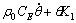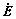?=ρh₀-div₀q₀                   (10)

where

K₁=,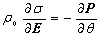

C_E and K₁ stand for the specific heat capacity and the thermal expansion property of material, respectively. q₀ is dependent on the temperature gradient function. The distribution heat source h doesn’t exist at the initial process of tension, and the temperature gradient is not obvious, then the right part of Eqn.(10) is equal to zero. Therefore, the equation becomes

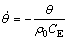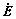K₁?                          (11)

It is shown in Eqn.(11) that the temperature of material falls in the thermoelastic state in the initial process of tension.

2.3 Rheological nonequilibrium

As the deformation increasing, the high polymer material experiences a deformation from elastic deformation to elastic-plastic deformation, and then forms elastic-viscoplastic deformation at last^[3-4]. The large deformation isn’t adapted to certain linear phenomenological relations, so the non-linear nonequilibrium state should be considered in view of thermomechanics. In Ref.[5], the strain energy density theory was used to obtain the energy dissipation relation in nonequilibrium state:

                            (12)

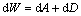                              (13)

where  A=A(H , F); W and V stand for the energy of unit volume and the change rate of volume with area dV/dA which is a dynamic variable, respectively. The present value of λ defines an energy state that has been given. F, A and D stand for deformation gradient, available energy density and dissipation energy density, respectively. Function H is used as an indication of order of the system under consideration. Obviously, dissipation energy density D is positive, corresponding to the entropy production d_iS in unit volume. The available energy density A can be either positive or negative, corresponding to the entropy flux d_eS. Based on that theory, equation of relations between nonequilibrium temperature Θ and irreversible dissipation energy density D was obtained according to Ref.[6]:

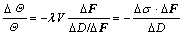               (14)

where  σ=∫ λVdF, stands for stress.

Based on Eqn.(14), Θ and D can be calculated. It can be proved by either theory or experiment that an obvious strain gradient exists in the zone with defect and there is not enough time for heat transferring when material is under tensile load, therefore, temperature at crack tip rises obviously in the process of crack expansion^[7-8].

3 Thermomechanical coupling experiment

3.1 Sample making and hardware test^[9]

The sample material used PVC sheet (10 mm in thickness) which was manufactured into samples with the length 100 mm and width 75 mm. The width of two-end gripping is 85 mm and the connecting part of gauge length used R5 circle is transition (shown in Fig.1). The material testing machine (SHT 4305, shown in Fig.2) was used to do extension test for the materials with two kinds of microbores (d2 mm, d5 mm) at different strain rates (10, 20 and 30 mm/min).

Fig.1 Testing samples of PVC sheet

Fig.2 Material testing machine

3.2 Surveying results

The samples with different sizes of microbores were tested by extension under different strain rates, being limited in length of this manuscript. This paper gives only a part of the results. The experimental results of specimen with the size of microbores of d5 mm under tension rate of 10 mm/min are chosen in this paper.

4 Analysis of experimental results

1) Fig.3 shows that the temperature of area close to microbores is lower than that of the other part of the specimen in elastic deformation process, and the minimum temperature (25.9 ℃) is lower than the room temperature (27.3 ℃). The temperature falls apparently.

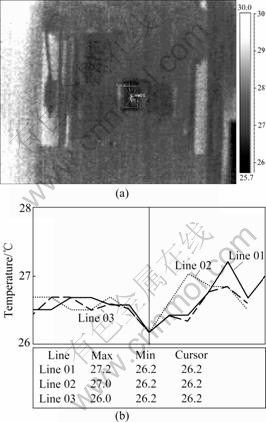
Fig.3 Field of temperature in initial process of tension (The three lines in Fig.3(b) are corresponding to the temperature changes of the three lines in Fig.3(a). Perpendicular in Fig.3(b) stands for the position of the microbore.)

2) It is shown in Fig.4 and Fig.5 that the temperature of the microbore is higher than that of the other part of specimen in the initial rupture process, but the temperature of other part is lower than the room temperature. Fig.6 shows the temperature distribution histogram.

3) When large-scale rupture happens, as shown in Fig.7 and Fig.8, the temperature rises as the microbore for the center along with the direction of the expansion of crack and falls along with the other directions. The peak temperature can reach 41.3 ℃, and the greatest temperature difference is 14.2 ℃. Fig.9 shows the temperature distribution histogram.

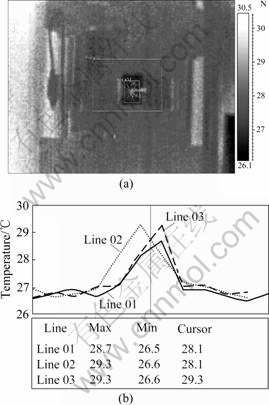
Fig.4 Field of temperature in initial rupture process

Fig.5 3-D cloud image of temperature corresponding to Fig.4

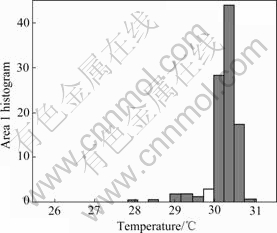
Fig.6 Temperature distribution histogram corresponding to area 1 in Fig.4(a)

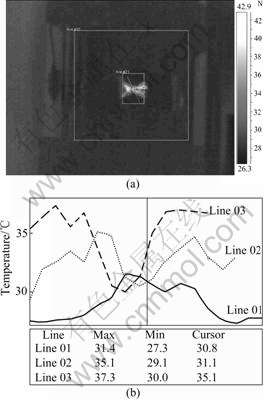
Fig.7 Field of temperature when large-scale rupture happens

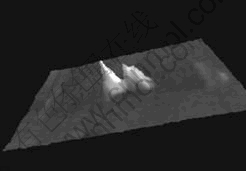
Fig.8 3-D cloud image of temperature corresponding to Fig.7

Fig.9 Temperature distribution histogram corresponding to area 1 in Fig.7(a)

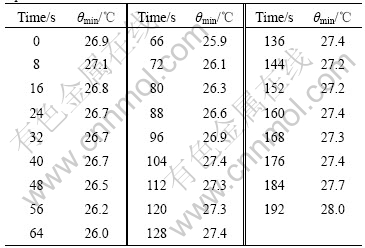
4) The minimum temperature always appears when the specimen is yielded, which also further proves the conclusion in Ref.[3]. It is shown obviously in Table 1 that in the rupture process of material the minimum temperature of the process zone falls firstly, and then arises. And the highest temperature falls at the beginning, then arises suddenly because of the new surface caused by the rupture, and then falls a little. The temperature of the craze zone arises apparently, and the temperature of crack tip reaches the maximum. The appearance of craze is the material basement of the formation of dissipative structures, which needs certain energy to maintain in the transformation between mechanical energy and thermal energy.

Table 1 Time history of θ_min in fracture process zone at crack tip

5) In the condition of the same diameter of microbores, there is an obvious nonlinear relationship between different extension rates and rupture time. There is difference in maximum loading and temperature change between samples with different diameters of microbores at the same extension rate. The smaller the diameter of microbores is, the more the temperature falls. The research on the difference in temperature dissipation caused by the distribution of microbores needs a further research.

References

[1] HUANG Z P. Fundamentals of continuum mechanics [M]. Beijing: Higher Education Press, 2003. (in Chinese)

[2] YUAN Long-wei. Failure theory and application of rheology material with defects [M]. Beijing: Science Press, 2001. (in Chinese)

[3] YUAN Long-wei. The rheo-failure theory of time-dependent materials containing defects[J]. Natural Science Journal of Xiangtan University, 2003, 25(4): 1-21. (in Chinese)

[4] YUAN Long-wei. On the basic equation group of rheological material containing defects [J]. Natural Science Journal of Xiangtan University, 2000, 22(3): 113-121. (in Chinese)

[5] SIH G C. Thermomechanics of nonequilibrium and irreversible processes (I) [J]. Advances In Mechanics, 1989, 19(2): 16-29. (in Chinese)

[6] SIH G C, TZOU D Y, Heating preceded by cooling ahead of crack: Macrodamage free zone [J]. Theory Appl Fracture Mech, 1986, 6(2): 103-111.

[7] YUAN Long-wei. An unified equation of macro-/meso-/microscopic stratum system for rheological material containing defects in failure process [J]. Natural Science Journal of Xiangtan University, 1999, 21(4): 130-136. (in Chinese)

[8] LUO W B, YANG T Q, LI Z D, YUAN L W. Experimental studies on the temperature fluctuations in deformed thermoplastics with defects [J]. Solids Structures, 2000, 37(6): 887-897.

[9] LUO Ying-she, SU Jian-xin, DENG Xu-hua, CHEN Wei. Exploitation and applicating research on surveying system of pyromagnetic effect during rupture process of PVC sheet with defects [J]. Applied Mechanics and Engineering, 2003, 8: 277-282.

(Edited by CHEN Wei-ping)

Foundation item: Project(10672191) supported by the National Natural Science Foundation of China; Project(06JJ2059)supported by the Provincial Natural Science Foundation of Hunan, China; Project(KF0607) supported by the Key Laboratory of Low Dimensional Materials and Application Technology (Xiangtan University), Ministry of Education, China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: LUO Ying-she, Professor, PhD, Tel: +86-731-5623376; E-mail: lys0258@sina.com