文章编号:1004-0609(2013)07-1954-09
外加应力下Ni2MnGa合金中马氏体孪晶变体再取向动力学的相场模拟
万见峰,张骥华,戎咏华
(上海交通大学 材料科学与工程学院,上海 200240)
摘 要:利用相场方法研究Ni2MnGa形状记忆合金中不同连续拉应力方向马氏体孪晶变体的再取向动力学。模拟结果表明:施加应力方向决定体系演化的最终结构和演化路径,沿[100]和[110]方向施加应力分别得到单变体和双变体,而沿[111]方向施加应力,体系依然保持为3种变体。计算了相应的与界面动力学因子和切变模量相关联的孪晶化应力,计算结果与实验结果接近。加载和卸载后2种变体和3种变体之间的组织转化具有可逆性。
关键词:Ni2MnGa合金;马氏体孪晶变体;再取向动力学;孪晶化临界应力;相场模拟
中图分类号:TF777.1 文献标志码:A
Phase-field simulation of reorientation kinetics of martensitic twin variants in Ni2MnGa alloy under external stress
WAN Jian-feng, ZHANG Ji-hua, RONG Yong-hua
(School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract: The kinetics of reorientation of martensitic twin variants under the continuous tensile stress along different directions in Ni2MnGa shape memory alloys was investigated by phase-field method. The simulated results reveal that the final morphology and the pathway of microstructural evolution depend on the stress-applied direction. The single variant and two variants can be obtained when the external stress is applied along [100] and [110] directions, respectively, while three variants still exist when the stress is applied along [111] direction. The corresponding twinning stress related to interfacial dynamic factor and shear modulus was calculated, which is close to the experimental measurements. The structural evolution between two variants and three variants has good reversibility during loading and unloading.
Key words: Ni2MnGa alloy; martensitic twin variants; reorientation kinetics; critical twinning stress; phase-field simulation
Ni2MnGa合金中通过磁场或应力场可获得较大的应变输出,这主要是马氏体变体的再取向和再分布造成的[1]。 实验结果显示,若只有外磁场,需要达到2 T才能获得较大的应变输出[2]。但问题是要产生2 T的磁场装置比较大,比器件本身的体积要大很多,这严重限制了基于此效应驱动器件的工业应用。目前,比较实用的方法是同时加上应力场和磁场,且两者的方向相互垂直[3]。外加应力场可有效减小磁场,实验结果显示,在一定的应力场下,磁场已降到1 T以下,同时磁场下的输出应变也有保证[4]。显然应力场的作用非常重要,它能有效地降低磁场,而且加应力场比加磁场方便得多,应力场的大小也容易调节。但目前的研究结果显示,加应力场还没有任何规律可循,都是凭经验来选择施加应力场的大小。另外,孪晶化应力是一个非常重要的参数,它直接关系到Ni-Mn-Ga合金的应变输出。在较早的文献中报道Ni2MnGa合金孪晶化应力为15~20 MPa[5],随后,此应力降低到2~3 MPa[6-7]。最近研究发现,在Ni2MnGa单晶合金中,孪晶化应力只有0.1 MPa,10次循环加载后,此应力增加到0.8 MPa [8]。在这些研究中,加载方向不同,得到的实验结果不同,所以有必要系统地研究不同加载方向对孪晶化应力的影响,从而得到有规律的结果,为此类材料的实际应用奠定基础。 本文作者利用相场的方法研究Ni2MnGa合金马氏体变体在[100]、[110]和[111]方向施加连续应力后再取向的机制和演化路径,并计算马氏体各变体转换的临界应力,同时考虑界面动力学因子和切变模量对此临界值的影响。
1 相场方法
系统的Ginzburg-Landau自由能(F)包括化学自由能(Fch)、界面能(Fin)和弹性应变能(Fel)[9]:
F=Fch+Fin+Fel (1)
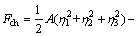
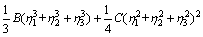 (2)
(2)
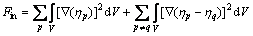 (3)
(3)
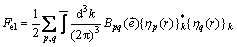
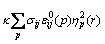 (4)
(4)
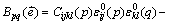
 (5)
(5)
式中:A、B和C是Landau自由能系数;{h1,h2,h3}是长程序参量,分别对应马氏体的3种变体;对于界面能,包括马氏体/奥氏体界面能和马氏体孪晶界面能,分别对应式(3)右边的第一项和第二项,这与文献[9]有所差别,也不同于其他界面[10];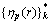 是
是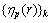 的复共轭;
的复共轭;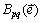 是二体交互作用势;Cijkl是弹性常量;
是二体交互作用势;Cijkl是弹性常量;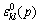 是p变体的相变应变。
是p变体的相变应变。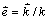 (
(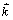 是倒易点阵矢量);
是倒易点阵矢量);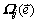 是格林函数张量,满足
是格林函数张量,满足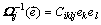 ,其中ek是
,其中ek是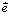 的k阶分量。外应力分别对应[100]、[110]和[111] 3个方向。k=1表示施加外应力;k=0表示取消外应力。基于时间的Ginzburg-Landau方程,其非守恒结构序参量
的k阶分量。外应力分别对应[100]、[110]和[111] 3个方向。k=1表示施加外应力;k=0表示取消外应力。基于时间的Ginzburg-Landau方程,其非守恒结构序参量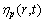 利用变分原理可得到
利用变分原理可得到
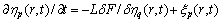 (6)
(6)
式中:L是微观结构演化的动力系数;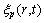 是Langevin噪声项,服从Gaussian分布,用来表示热扰动。联立方程(1)~(5),其演化动力学方程为表示为
是Langevin噪声项,服从Gaussian分布,用来表示热扰动。联立方程(1)~(5),其演化动力学方程为表示为
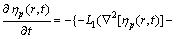
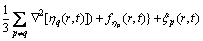 (7)
(7)
式中: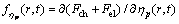 ,L=6L1。 在数值模拟过程中常采用约化的形式以方便计算,其约化的时间和空间分别为
,L=6L1。 在数值模拟过程中常采用约化的形式以方便计算,其约化的时间和空间分别为 和
和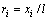 。 相变驱动力Δf(T)可表示为
。 相变驱动力Δf(T)可表示为 ,其中Q 、T 和T0分别表示马氏体相变潜热、相变温度和平衡温度。计算网格为N0×N0×N0,其长度单位为l。其他无维参量如下:
,其中Q 、T 和T0分别表示马氏体相变潜热、相变温度和平衡温度。计算网格为N0×N0×N0,其长度单位为l。其他无维参量如下:
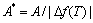 ,
,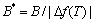 ,
,
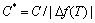 ,
,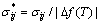 ,
,
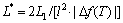 ,
,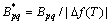 。
。
利用半隐格式傅里叶谱方法[11],在傅里叶空间,偏微分方程(7) 可写成无维的形式:
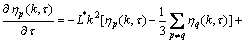
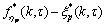 (8)
(8)
基于欧拉方法,给出如下改进的半隐格式形式:
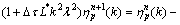
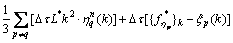 (9)
(9)
基于以上方法,对Ni2MnGa合金中的FCC→FCT相变进行模拟。在弹性各向同性体系中格林矢量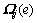 可表示为
可表示为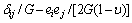 ,其中,
,其中,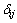 为Dirak delta函数,G为切变模量,
为Dirak delta函数,G为切变模量,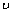 为泊松比。沿[100]和[110]方向的应力加载速率为每100时间步长0.004 MPa,而沿[111]方向上的应力加载速率为每100时间步长0.01 MPa。Ni2MnGa合金的切变模量G为30 GPa,泊松比
为泊松比。沿[100]和[110]方向的应力加载速率为每100时间步长0.004 MPa,而沿[111]方向上的应力加载速率为每100时间步长0.01 MPa。Ni2MnGa合金的切变模量G为30 GPa,泊松比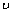 为0.38[12]。具体计算模拟中,T=300 K, Df(T)=1.5×107 J/m3,A*=0.3,B*=4.5,C*=4.2,e0(T)=-0.02[13-14]。约化时间Dt=0.02,计算单胞采用周期性边界条件,计算网格N0=64。
为0.38[12]。具体计算模拟中,T=300 K, Df(T)=1.5×107 J/m3,A*=0.3,B*=4.5,C*=4.2,e0(T)=-0.02[13-14]。约化时间Dt=0.02,计算单胞采用周期性边界条件,计算网格N0=64。
2 模拟结果及分析
2.1 初始组织
在施加应力前,需要得到Ni2MnGa合金初始相变组织。图1所示为Ni2MnGa合金体系微观组织随时间的演化过程。图1(d)所示为演化10 000步后微观组织的形貌,将其作为应力拉伸的初始结构。从其演化过程可得到以下结果:(1) 在Ni2MnGa合金中马氏体孪晶的形成过程中,3种马氏体变体具有很好的孪晶关系,孪晶面为(110);变体1(V1)和变体2(V2)相对变体3(V3)为大片结构,而且变体3作为细片结构镶嵌在变体1和2中。但这种良好的孪晶结构并不是一开始就形成的,在相变初期,如图1(a)所示,3种变体呈随机分布,没有孪晶关系,表明相变不借助于孪晶形核机制。随着时间的延长,相变的体积分数和体系的应变能都增加,单一马氏体片逐步长大,变体间的相互协调增强,一些区域开始形成孪晶,如图1(b)所示,在运行1 000步后,体系的大部分区域已形成孪晶。(2) 在Ni2MnGa合金大片马氏体的长大过程中,变体1和2尽管呈现大片结构,但其不是一开始就形成的,而是小变体相互融合长大的,这可从图1(b)演化到图1(c)的过程中看出。(3)变体组织的分布规律:一种变体在另外一种变体内只能相互平行,不能交叉,这样体系的能量才能保持最低,根据图1,变体3在变体1和2中最终都相互平行。
2.2 沿[100]方向拉伸时Ni2MnGa合金微观组织的演变
以图1(d)作为初始组织,在[100]方向上对Ni2MnGa合金体系施加连续拉应力最终可得到单变体。图2所示为其演化的具体过程。从图2可以看出,变体2逐渐变薄,变体1相应增厚,这个转变过程主要靠变体1和变体2之间的孪晶界面运动来实现,这种转变是变体间的相互转化,不属于相变过程,也不同于孪晶变形[15]。同时,在变体1和变体2中的变体3 逐渐消失,最后完全消失,剩下变体1和变体2,但此时变体2的含量较低,需要进一步增加拉应力才能让变体2彻底消失,最终只剩下单变体1。值得注意的是,变体3在变体2中先消失,在变体1中后消失,这表明变体3在变体1和变体2中的应力状态不同,而内应力对相变是有影响的[16]。变体3尽管均受到拉应力的作用,但变体1在增加,而变体2在减少,前者导致变体3宽度增加,后者导致变体3宽度减小。同时变体3的消失过程同样依靠马氏体孪晶界面的移动来完成。从另外一个角度讲,在拉应力下,逐渐增加的变体1会减缓变体3的消失速度,而逐渐减少的变体2却促进变体3的消失。图2(g)所示为Ni2MnGa合金体系各变体的体积分数与外加应力之间的关系,由此可判断变体相互转化的临界应力。从图2(g)中看出,变体2和变体3完全消失所需的应力不同,分别对应A点和B点,这与上面的结构演化是一致的,且此临界拉应力均小于0.06 MPa,这与实验结果[8]基本符合。另外,应力作用下除了变体间的相互转化外,还存在微量的应力诱发马氏体相变;在图2(a)中存在少量的母相,当施加应力后,母相进一步减少,最后均成为变体1。
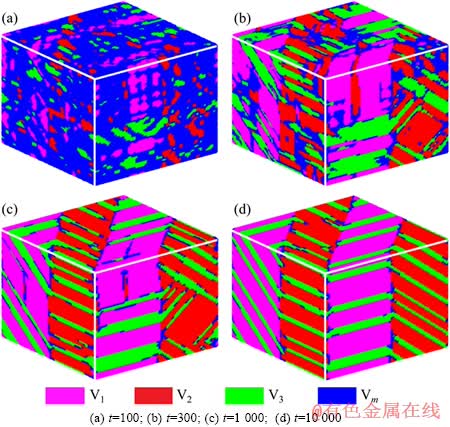
图1 G=30 GPa、L*=0.5时Ni2MnGa合金体系微观组织随时间演化过程
Fig. 1 Microstructural evolution of Ni2MnGa alloy system with time at G=30 GPa and L*=0.25
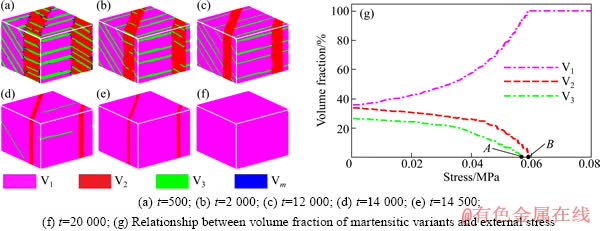
图2 在[100]方向连续施加拉应力下Ni2MnGa合金体系微观组织的演化过程及马氏体变体体积分数与外应力的关系
Fig. 2 Microstructural evoluation of Ni2MnGa alloy system along [100] direction under continous tensile stress and relationship between volume fraction of martensitic variants and external stress
2.3 沿[110]方向拉伸时Ni2MnGa合金微观组织的演变
在Ni2MnGa合金体系的[110]方向上施加拉应力时,体系最后变成2种变体,变体1(V1)和变体2(V2)(图3)。在此方向上施加拉应力,变体3(V3)逐步消失,而变体1和变体2几乎没有变化,变体1和2的孪晶界面也没有太明显的迁移,表明[110]方向上施加应力对变体1和变体2有利,而对变体3则是反向作用。在应力作用下,借助变体1与变体3、变体2与变体3之间的孪晶界面迁移完成了变体间的相互转换,这个过程不属于固态相变,仅仅是结构位相的变化。但也存在少量的应力诱发马氏体,因为图3(a)中的母相与图3(f)的母相相比已经减少,此方向的应力诱发可产生变体1和2。其中一个现象值得注意,在图3(b)中,应力作用下变体2中的变体3逐步消失,同时会诱发新的变体3,这种转变主要是在变体1和变体2的孪晶界面处形核和长大,并与原来的变体3在位向关系上相互垂直;随着应力的增加,这种新形成的变体3完全取代了原来的变体3,并呈相互平行的分布状态(图3(c)),然而,新形成的变体3在更大的外加应力下也是不稳定的,最后逐渐消失,如图3(d)~(f)所示。 而变体1中的变体3则没有出现这种新位相的诱发相变。 当应力达到A点时,变体3全部消失,得到外应力条件的2个变体的稳定体系。 同时得到外加应力下Ni2MnGa合金中各变体体积分数的变化关系曲线(图3(g)),当外应力达到0.085 MPa时,体系中变体3完全消失,只剩下变体1和变体2,并呈现良好的孪晶位向关系,但两种变体的体积分数并不完全相等。
2.4 沿[111]方向拉伸时Ni2MnGa合金微观组织的演变
根据晶体学位向关系,在[111]方向上施加应力对3个变体都有利,所以没有出现其中任何一个变体消失的现象,但Ni2MnGa合金中内部微观组织会产生变化,主要是变体1和变体2中变体3的位向和分布。图4所示为沿[111]方向拉伸时Ni2MnGa合金的微观组织演变。从图4(b)可看出,在外加应力作用下,在变体1和变体2的界面有另一种位向的变体3形成,并同原变体3相互交叉(垂直关系);随着外加应力的增大,此位向的变体逐渐增多,而与之垂直的同种变体逐渐减少,直至最后消失,如图4(f)所示。尽管在其过程中会出现同一种变体的相互交叉,但这种状态并不稳定,慢慢会形成位相一致的变体,并相互平行。需要注意的是,变体2中新变体3的出现是从变体1和变体2的孪晶界面处形核并长大的,而与之垂直的原变体3先从孪晶界面脱离,然后逐渐收缩,直至消失。图4(g)所示为外加应力下Ni2MnGa合金中各变体的体积分数的变化曲线。由图4(g)可看出,各变体的体积分数几乎没有太大的变化,大约在应力为0.14 MPa时,3种变体间有一个微小的调整过程,这应当对应于变体2中的变体3的位相调整,此后各变体的体积分数几乎未发生变化,而且母相还保持一定的残余量。对比图4(a)和(f),母相有所减少,表明也存在少量的应力诱发马氏体相变,同时产生了少量的变体1、2和3,但由于此应力对3种变体是等价的,残余的母相消失得比较慢,在演化结束时仍然保留了微量的母相。
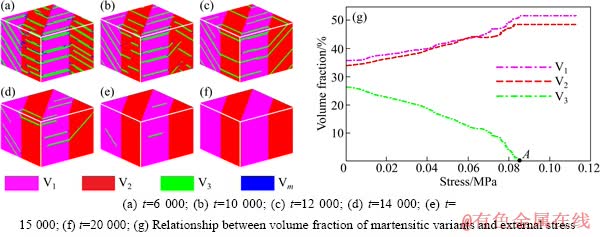
图3 沿[110]方向连续施加拉应力下Ni2MnGa合金体系微观组织的演化过程及马氏体变体体积分数与外加应力的关系
Fig. 3 Microstructural evoluation of Ni2MnGa alloy system under continous tensile stress along [110] direction and relationship between volume fraction of martensitic variants and external stress
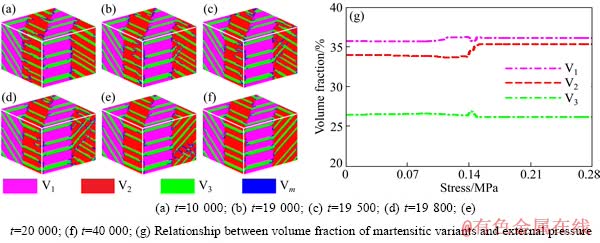
图4 沿[111]方向连续施加拉应力下Ni2MnGa合金体系微观组织的演化过程及马氏体体积分数与外加应的关系
Fig. 4 Microstructural evoluation of Ni2MnGa alloy system under continous tensile stress along [111] direction and relationship between volume fraction of martensitic variants and external pressure
3 讨论
3.1 界面动力学因子对Ni2MnGa合金临界应力的影响
考察界面动力学因子对Ni2MnGa合金临界压应力的影响,计算结果如图5(a)所示。界面动力学因子是反映界面运动能力的一个参数,其值越大,意味着界面迁移所需的能量越高,所需要的应力应当越大,而本文作者的计算结果是:对于Ni2MnGa合金体系,沿[100]方向施加拉应力时,其临界应力随动力学因子的增加而减小,此变化比较平缓;沿[110]方向的临界压应力也随动力学因子的增加而减小,但变化比较大;而沿[111]方向施加的拉应力时,由于没有出现变体的消失,所以不存在类似的临界应力,与此参数无太大的关系,在图5(a)中没有列出。要解释这种现象,需要从微观组织来分析。从图5(b)可看出,界面动力学因子对微观组织有一定的影响,界面动力学因子越大,体系的组织就越粗大(Ini为初始组织),主要体现在变体1和变体2中的变体3的厚度随界面动力学因子的增加而增大(图5(b))。当界面动力学因子分别为0.35和0.1时,对比施加应力前的组织可以看出,较小的界面动力学因子可以使体系的变体3在变体1和变体2中的分布更均匀,薄片数目更多、厚度更薄。由于变体3的两端分别同变体1或变体2的孪晶边界相连,这样在不同方向上施加应力后,在界面上钉扎较少的马氏体更容易推动,容易实现变体的再取向,因此,界面动力学因子越小,尽管单片马氏体的轴向已运动,但端部由于孪晶界面的阻碍作用反而不利于整片马氏体的运动,这属于界面的钉扎拖曳效应。另外,还有一个阻碍作用,即Ni2MnGa合金中马氏体片的数目增多,马氏体片相互之间的作用增强,在界面动力学因子较小的体系中,变体3的片数明显较多,所以,它们之间的相互作用强于马氏体片数较少体系的相互作用,所受到的阻力就增大,这属于平行马氏体片的相互作用机制。这两种效应共同决定了界面动力学因子对临界应力的反常变化。
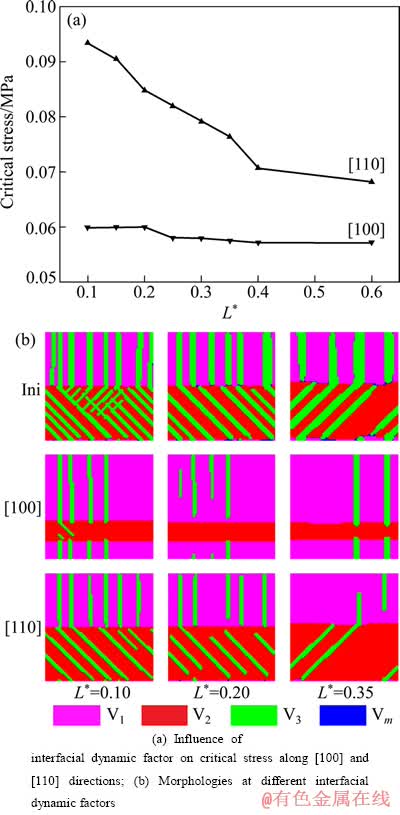
图5 界面动力学因子(L*)对Ni2MnGa合金在[100]、[110]方向临界拉应力及组织形态的影响
Fig. 5 Influence of interfacial dynamic factor (L*) on critical stress and morphology of Ni2MnGa alloy
3.2 切变模量对Ni2MnGa合金体系临界应力的影响
切变模量(G)对Ni2MnGa合金体系的临界拉应力有较大的影响,如图6(a)所示,随切变模量的增加,各个方向施加的临界应力都有较大的变化,均随切变模量的增加而增加。这可能与体系的弹性应变能有关,利用式(4)和(5)可计算得到Ni2MnGa合金体系的应变能与演化时间的关系,如图6(b)所示。从图6(b)可看出,体系平衡下的约化应变能随切变模量的增加而增加,表明切变模量越大,相变的阻力越大,体系达到平衡状态时各变体周围的应力场分布也不同。另一个阻力来自各变体间的相互作用,切变模量越大,这种相互作用也越大,这两种作用综合起来导致在施加外应力时各变体间相互转化所需要的临界应力也越大,由此可解释图6(a)的结果。另外,不同的切变模量下,材料体系的初始组织演化也不同,图6(c)所示为切变模量分别为25和45 GPa下体系(010)面微观组织随时间的演化过程。从图6(c)中可看出,在相变初期(t=100),切变模量大,不利于体系的形核, 演化10 000步后,体系内部组织有明显的差异,切变模量大的Ni2MnGa合金体系更易形成均匀分布的微观组织,这主要是由于变体间的相互作用较大,自协调效应起到主要的控制作用[17]。
3.3 应力松弛后Ni2MnGa合金体系的微观组织演化
TANAKA等[18]讨论了铁基合金的超弹性,发现应力松弛后马氏体能够发生逆转变,其中的力学行为比较复杂[19]。下面考察Ni2MnGa合金在外加应力下马氏体变体重排后去除应力,重排后的马氏体微观组织是否会回复到重排前的组织。这里,以[110]方向施加应力后的微观组织为初始组织,在其达到平衡状态后释放此应力,模拟结果发现微观组织发生了有趣的转变。 Ni2MnGa合金中在[110]方向施加应力后得到两个变体的亚平衡系统,去除应力后,消失的变体又重新形核并长大,但同初始组织有差别。图7所示为以图4(f)为初始态释放应力后的微观组织演化,反映变体3在变体1和变体2中的重新形成过程。从图7(c)可看出,变体3首先在变体1中形成,并逐渐长大,在变体1和变体3的孪晶界面推移过程中,孪晶界面存在明显台阶,表明界面迁移的过程是逐层进行的,并不是界面的整体迁移。当演化时间为1 300时(图7(d)),变体3开始在变体1和变体2的孪晶界面处形核并长大,而且是从孪晶界面一侧向平行的孪晶界面长大,直到碰到平行的孪晶界面,其长大过程也是借助于界面台阶逐步推移完成的。在变体1和变体2中的变体3各自之间也是相互平行的,这是一个自组织的行为,从而使体系的能量更低。将图7(f)与图3(a)比较,尽管体系都是3种变体,但内部组织仍然有明显的变化,主要是变体3在变体1和变体2中的分布发生了改变,表明经过应力拉伸和应力释放,可以对体系的内部组织进行微调,这是实现组织调控的一种方式,对于材料的工业应用具有一定的参考价值。
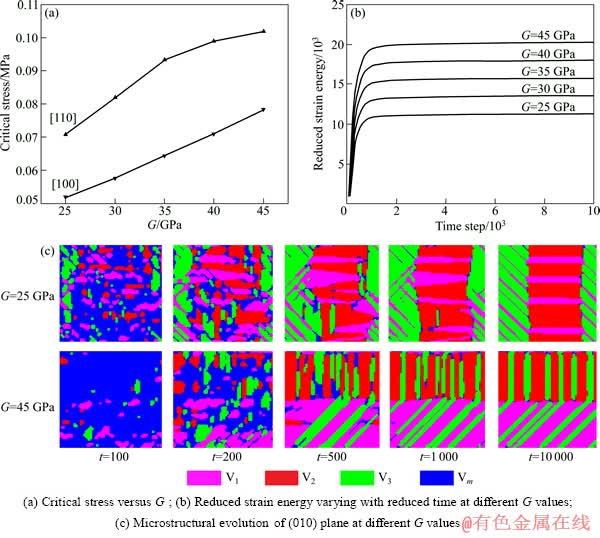
图6 切变模量(G)对Ni2MnGa合金体系临界应力、约化应变能及微观组织的影响
Fig. 6 Influence of shear modulus (G) on critical stress, reduced strain energy and microstructure of Ni2MnGa alloy system
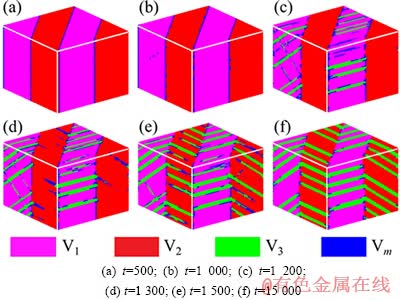
图7 应力松弛后Ni2MnGa合金体系微观组织的演化
Fig. 7 Microstructural evolution of Ni2MnGa alloy system after releasing loading
图8(a)所示为Ni2MnGa合金中3种变体的体积分数随时间的变化,在前600步,各变体的体积分数没有什么变化,这与图7(a)一致,内部的微观组织基本不变, 随后变体3的体积分数才有较大的变化,表明这是变体3形核的孕育期,但此阶段并没有形核。图8(b)所示为Ni2MnGa合金体系中3种变体各部分能量的变化。由图8(b)可知,在前600步界面能和应变能都没有变化,所以,此阶段没有形成变体3的核胚。600步后进入第二阶段,变体3在变体1和变体2中的形核并长大,尽管在图7(c)和(d)显示变体3在变体1中先形核长大,但变体3在整个体系中的形核长大时间并不长(小于400步),随后体系处于平衡状态,体系的体积分数(图8(a))和各部分能量(图8(b))基本保持不变。
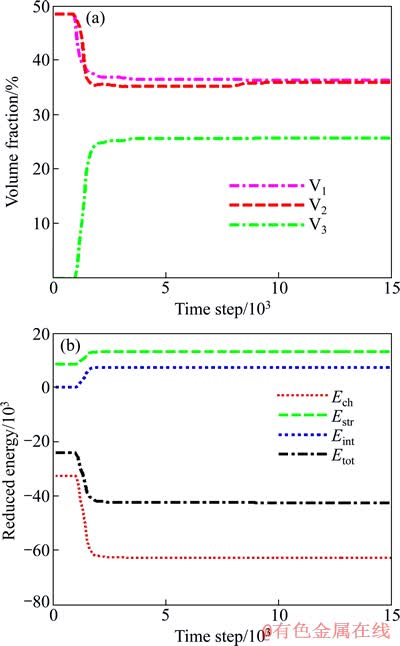
图8 3种变体的体积分数及体系各部分约化能量与演化时间的关系
Fig. 8 Relationship between volume fraction of three variants (a) and reduced energy (b) of Ni2MnGa alloy system varying with reduced time
4 结论
1) 基于相场模拟,系统研究Ni2MnGa形状记忆合金中的孪晶马氏体在[100]、[110]和[111]方向施加拉应力后的微观组织演化动力学。模拟结果表明,应力施加方向决定体系的演化路径及最终的组织形态。沿[100]方向施加拉应力,原体系转化为单变体;沿[110]方向施加拉应力,原体系转化为双变体;沿[111]方向施加拉应力,原体系仍为3种变体。
2) 采用理论计算方法讨论界面动力学因子和体系切变模量对孪晶化临界应力的影响,计算结果与实验结果比较符合。计算结果表明,界面动力学因子越大,体系的切变模量越小,则孪晶化临界应力越小。从体系的能量和微观组织演化的角度对其进行了合理的解释。
3) 应力松弛后,消失的变体会重新在孪晶界面形核并长大,且内部组织已发生重新排列。通过施加拉应力然后释放此应力,可实现材料内部微观组织的精细调控。
REFERENCES
[1] ULLAKKO K, HUANG J K, KANTNER C, O’HANDLEY R C, KOKORIN V V. Large magnetic-field-induced strains in Ni2MnGa single crystals[J]. Appl Phys Lett, 1996, 69(13): 1966-1968.
[2] LIKHACHEV A A, ULLAKKO K. Magnetic-field-controlled twin boundaries motion and giant magneto-mechanical effects in Ni-Mn-Ga shape memory alloy[J]. Phys Lett A, 2000, 275(1/2): 142-151.
[3] MA Y F, LI J Y. Magnetization rotation and rearrangement of martensite variants in ferromagnetic shape memory alloys[J]. Appl Phys Lett, 2007, 90(17): 172504-1-3.
[4] HECZKO O, SOROKA A, HANNULA S P. Magnetic shape memory effect in thin foils[J]. Appl Phys Lett, 2008, 93(2): 022503-1-3.
[5] MARTINOV V V, KOKORIN V V. The crystal structure of thermally- and stress-induced martensites in Ni2MnGa single crystals[J]. J Phys III France, 1992, 2: 739-749.
[6] WU P P, MA X Q, ZHANG J X, CHEN L Q. Phase-field simulations of stress-strain behavior in ferromagnetic shape memory alloy Ni2MnGa[J]. J Appl Phys, 2008, 104(7): 073906-1-5.
[7] CHERNENKO V A, L’VOV V A, MULLNER P, KOSTORZ G, TAKAGI T. Magnetic-field-induced superelasticity of ferromagnetic thermoelastic martensites: Experiment and modeling[J]. Phys Rev B, 2004, 69: 134410-1-8.
[8] STRAKA L, LANSKA N, ULLAKKO K, SOZINOV A. Twin microstructure dependent mechanical response in Ni-Mn-Ga single crystals[J]. Appl Phys Lett, 2010, 96(13): 131903-1-3.
[9] WANG Y, KHACHATURYAN A G. Three-dimensional field model and computer modeling of martensitic transformations[J]. Acta Mater, 1997, 45(2): 759-773.
[10] 伍 林, 陈 铮, 庄厚川, 黄勇兵, 杨 涛. 微观相场模拟B2-FeAl金属间化合物有序畴界的形成和迁移[J].中国有色金属学报, 2013, 23(3): 697-694.
WU Lin, CHEN Zheng, ZHUANG Hou-chuan, HUANG Yong-bing, YANG Tao. Microscopic phase-field simulation of formation and motion of ordered domain boundaries in B2-FeAl intermetallic compound[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(3): 697-694.
[11] CHEN L Q, SHEN J. Applications of semi-implicit Fourier-spectral method to phase field equations[J]. Comp Phys Commu, 1998, 108(2/3): 147-158.
[12] KART S O, CAGIN T. Elastic properties of Ni2MnGa from first principles[J]. J Alloys Comp, 2010, 508(1): 177-183.
[13] PONS J, CHERNENKO V A, SANTAMARTA R, CESARI E. Crystal structure of martensitic phases in Ni-Mn-Ga shape memory alloys[J]. Acta Mater, 2000, 48(12): 3027-3038.
[14] KUO Y K, SIVAKUMAR K M, CHEN H C, SU J H, LUE C S. Anomalous thermal properties of the Heusler alloy Ni2+xMn1-xGa near the martensitic transition[J]. Phys Rev B, 2005, 72(5): 054116-1-10.
[15] 黄 文, 汪 洋, 李子然, 夏源明. 温度和应变率对多晶纯钛孪晶变形的影响[J]. 中国有色金属学报, 2008, 18(8): 1440-1445.
HUANG Wen, WANG Yang, LI Zi-ran, XIA Yuan-ming. Influences of temperature and strain rate on deformation twinning of polycrystalline titanium[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(8): 1440-1445.
[16] 宋瑞宁, 朱 伟, 刘恩克, 李贵江, 陈京兰, 王文洪, 李 祥, 吴光恒. 内应力对Mn2NiGa铁磁形状记忆合金的结构、相变和磁性能的影响[J]. 物理学报, 2012, 61(2): 027501-1-6.
SONG Rui-ning, ZHU Wei, LIU En-ke, LI Gui-jiang, CHEN Jing-lan, WANG Wen-hong, LI Xiang, WU Guang-heng. Effect of internal stress on structure, martensitic transformation and magnetic properties of ferromagnetic shape memory alloy Mn2NiGa[J]. Acta Phys Sin, 2012, 61(2): 027501-1-6.
[17] BHATTACHARYA K. Self-accommodation in martensite[J]. Arch Rational Mech Anal, 1992, 120: 201-244.
[18] TANAKA Y, HIMURO Y, KAINUMA R, SUTOU Y, OMORI T, ISHIDA K. Ferrous polycrystalline shape-memory alloy showing huge superelasticity[J]. Science, 2010, 327(5972): 1488-1490.
[19] 周 博, 刘彦菊, 冷劲松, 邹广平.形状记忆合金的宏观力学本构模型[J]. 中国科学: G辑, 2009, 39(7): 998-1006.
ZHOU Bo, LIU Yan-ju, LENG Jing-song, ZOU Guang-ping. A macro-mechanical constitutive model of shape memory alloys[J]. Sci China: Ser G, 2009, 52(9): 1382-1391.
(编辑 陈卫萍)
基金项目:国家重点基础研究发展计划资助项目(2012CB619400);国家自然科学基金资助项目(51171112)
收稿日期:2012-08-28;修订日期:2013-03-22
通信作者:万见峰,副教授,博士;电话:13916496412;E-mail:jfwan@sjtu.edu.cn