DOI: 10.11817/j.issn.1672-7207.2015.11.036
基于分数阶微积分的变参数黄土蠕变损伤模型
唐皓1, 2,王东坡1,段钊3,赵法锁2,宋飞2,齐笛2
(1. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都,610059;
2. 长安大学 地质工程与测绘学院,陕西 西安,710054;
3. 西安科技大学 地质与环境学院,陕西 西安,710054)
摘要:为了准确认识黄土的流变特性,以不同含水率的咸阳Q2黄土为研究对象,采用分级加载的方式进行室内三轴蠕变试验,获得该黄土蠕变试验数据和曲线。选用包含软体元件的四元件蠕变模型来模拟黄土的流变。借鉴变参数牛顿元件的建造思路,应用SN元件及引入能反映应力水平、时间及含水率影响的损伤变量,改进四元件蠕变模型中的2个常参数软体元件为变参数软体元件,得到能反映黄土非线性流变及损伤特征的蠕变模型。利用黄土蠕变试验数据对改进所得的模型进行验证。研究结果表明:该模型在描述黄土整体流变特征时具有较好的效果。
关键词:黄土;软体元件;SN元件;非线性;损伤;模型
中图分类号:TU452 文献标志码:A 文章编号:1672-7207(2015)11-4248-08
Variable parameters creep damage model of loess based on fractional calculus
TANG Hao1, 2, WANG Dongpo1, DUAN Zhao3, ZHAO Fasuo2, SONG Fei2, QI Di2
(1. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,
Chengdu University of Technology, Chengdu 610059, China;
2. School of Geology Engineering and Geomatics, Chang’an University, Xi’an 710054, China;
3. College of Geology and Environment, Xi’an University of Science and Technology, Xi’an 710054, China)
Abstract: Triaxial creep test was performed on the Xianyang Q2 loess specimen at different moisture contents with multi-staged loading condition to obtain the creep curves of the loess material for better characterization on its rheological properties. A four-element creep model containing soft-matter element was selected to simulate the rheology of loess specimen. On the basis of the variable parameter Newton element with the application of SN element and damage variables for stress level, times and moisture content, the proposed creep model reflected the nonlinear rheological and damage characteristics of loess specimen was obtained by modifying two constant parameters in the soft-matter elements of the conventional four-elements creep model into variable parameters. The proposed creep model was validated by experimental results. The results show that the model can well characterize the rheological properties of loess specimen.
Key words: loess; soft-matter element; SN element; nonlinear; damage; model
近年来随着西部经济迅速发展,涉及黄土高原区的工程建设越来越多,由此引发的黄土次生灾害也相应增多,如黄土边坡失稳引发的滑坡灾害、黄土地基湿陷引起的不均匀沉降等。要充分认识和防治以上灾害,需要对黄土的物理及力学性质进行全面研究。实践表明,黄土流变特性在工程建设中表现尤其明显[1]。而充分认识黄土流变特性的主要手段是探寻适合描述其流变的本构模型。截至目前,已有较多学者通过室内试验的方式,从试验结果分析出发,应用多种理论建立了不同的黄土流变模型。归纳起来,主要是应用元件模型进行串并联组合建模;改进以往的线性元件为非线性元件再进行组合建模;引入损伤变量及演化方程建立损伤流变模型。如郭增玉等[2]在描述黄土黏弹性、黏塑性特征时分别采用了五元件的Kelvin分项模型及应用maxwell模型串联单个经验模型再并联单个理想塑性元件组合构建的分项模型,最终将2个分项模型串联得到1个可以表征高湿度Q2黄土非线性流变特征的总模型。朱才辉等[3]在研究压实区Q3黄土蠕变特性时,采用串联Kelvin模型与Burgers模型的方式得到了复合M-B模型,模型具有较好的黄土流变特性表征能力。谢星等[4]从黄土流变时会产生损伤的角度出发,基于应变等效原理在考虑损伤门槛的基础上构建了考虑瞬时损伤的黄土非线性流变模型。王东红等[5]在谢星的研究基础上,同时考虑黄土在流变过程中产生的瞬时损伤及突变破坏时的蠕变损伤进而构建了相应的黄土三维流变模型。上述模型的共同点在于应用Kelvin模型反映黄土的黏弹流变特性、而对于黄土的塑性、黏塑性描述则主要应用改进的黏塑元件或损伤理论来实现。虽然由上述技术体系构建的众多黄土流变模型均能较好地描述黄土流变各阶段特征,但多数模型整体结构较复杂,应用的基本元件数量较多,从而需要求解分析的参数较多,于工程建设中难以快速应用推广。殷德顺等[6]提出了一种新的类黏滞元件——软体元件。其应用分数阶微积分表征软体元件的本构关系,描述介于理想固体与理想流体之间的岩土材料流变特性。该元件所表述的物理意义清晰,结构简单,涉及参数少,具有极强的流变理论及实践研究意义。郭佳奇等[7]则应用该软体元件替换Kelvin-Voigt模型中牛顿元件,得到了分数阶微积分的Kelvin-Voigt模型,并应用页岩单轴压缩蠕变试验结果对其进行了验证,取得了较好的效果。孙海忠等[8]则利用含软体元件的Kelvin模型对南沙软土进行了模拟,结果表明模型不仅对软土蠕变试验结果拟合较好,还能反映材料的应力松弛现象。丁靖洋等[9-10]则通过引入损伤变量,提出了变黏性系数的Abel黏壶元件(软体元件),并用其替换了西原模型中的牛顿元件,建立了改进的西原模型,最后应用盐岩蠕变试验数据对模型进行了验证,取得了较好的效果。此外,Welch等[11-12]应用分数阶微积分理论对高分子聚合材料进行了黏弹性研究。宋勇军等[13-14]则应用分数阶微积分构建了一种新的非线性岩石蠕变模型。陈军浩等[15]则将分数阶微积分运用到了人工冻土蠕变特性分析中。陈亮等[16]则以分数阶微积分为基础构建了一种新的岩石四元件蠕变模型。Beda等[17]则基于材料的黏弹特性,提出了一种分数阶导数模型流变参数确定的新方法。本文作者在上述研究的基础上,基于分数阶微积分的特点,引入SN元件及考虑应力水平、时间及含水率因素的损伤变量,构建变参数软体元件,再按照黄土蠕变特点,尝试建立一个参数尽可能少、具有较强物理意义且能反映黄土整体蠕变的损伤模型。
1 黄土蠕变试验
1.1 试验材料及方法
试样取自陕西省咸阳市礼泉县某黄土崩塌坡脚处天然Q2黄土。野外采取的土样经过室内加工,统一制作成直径为39.1 mm、高度为80 mm的圆柱形试样。按照试验目的,采用水膜迁移法对所有试样进行人工增湿,得到4种不同含水率(8%,13%,17%和23%)的Q2黄土试样。
蠕变试验所用的仪器为CSS-2901TS型土体三轴流变试验机。试验采用分级加载的方式进行,围压恒定在50 kPa。试验前应用常规三轴固结不排水试验得出不同含水率试样的破坏强度,预先规定蠕变试验的加载级数N,然后确定每级加载的荷载增量。试验时每级加载持续12 h,待试样变形稳定后,再加下一级荷载。
1.2 含水Q2黄土蠕变特性
基于Boltzmann叠加原理将分级加载下的黄土蠕变试验数据转化为分别加载下的试验结果,对相应的试验结果进行分析得到不同含水率下的Q2黄土试样于围压50 kPa下的应变-时间曲线簇,如图1所示。从图1可知:不同含水率下的Q2黄土蠕变具有下述特征:1) 不同含水率的黄土试样在蠕变过程中,均能出现不同程度的3阶段蠕变(减速蠕变、等速蠕变及加速蠕变)。2) 不同含水率下的黄土试样在加载瞬时均表现一定程度的瞬时变形,且瞬时变形与加载应力呈现近似正相关关系。3) 相同围压时,在相同荷载下黄土的蠕变变形随着含水率增高而增大。4) 黄土的蠕变变形存在一应力临界值,当加载应力小于临界值时,黄土表现出衰减稳定,且达到稳定所需时间较短,随后蠕变以接近0的恒定速率继续稳定。5) 当加载应力高于临界值时,黄土试样会表现出加速蠕变破坏,且随着含水率的增大,其加速蠕变至破坏时间减小。6) 不同含水率下的黄土试样加速蠕变所对应的临界应力随着含水率增大而减小。

图1 Q2黄土三轴蠕变试验曲线
Fig. 1 Curves of triaxial creep experiments of Q2 loess
2 基于分数阶微积分的黄土蠕变模型
2.1 R-L型分数阶微积分
分数阶微积分是在传统整数阶微积分理论基础上发展而来,其核心变化在于微积分阶数从整数拓展到分数、复数层面。分数阶微积分的出现标志着微积分理论的壮大与完善。相比较整数阶微积分,分数阶微积分具有以下优点:首先,分数阶导数具有全局相关,能较好地体现系统函数发展的历史依赖过程;而整数阶导数具有局部性,不适合描述有历史依赖过程的情形。其次,分数阶导数模型克服了经典整数阶微分模型理论与实验结果吻合不好的严重缺点,使用较少几个参数就可获得很好的效果。最后,在描述复杂物理力学问题时,与非线性模型比较,分数阶模型的物理意义更清晰,表述更简洁。
当前,许多数学工作者从不同的角度给出了不同的分数阶微积分定义。如Riemann-Liouville型、Grunwald-Letnikov型及Caputo型[18]。其中Riemann- Liouville型以其应用简练且效果优良而得到较广泛应用,其具体表述如下。
函数 的β阶积分定义为
的β阶积分定义为
 (1)
(1)
分数阶微分则定义为
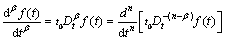 (2)
(2)
式中: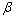 >0,且n-1<
>0,且n-1<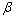 ≤n(n为正整数);Γ(
≤n(n为正整数);Γ(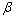 )为Gamma函数,
)为Gamma函数,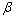 的实部大于0,其定义为
的实部大于0,其定义为
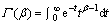 ,Re
,Re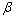 >0 (3)
>0 (3)
2.2 分数阶微积分软体元件
传统的流变理论模型由基本的理想弹性、黏性及塑性元件经过串并联构建。其中理想弹性元件为虎克体,其本构关系方程可以表述为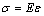 。理想黏性元件为牛顿体,其本构关系方程可以表述为
。理想黏性元件为牛顿体,其本构关系方程可以表述为 。按照微分数学知识,可以将虎克体与牛顿体的本构关系方程改写为
。按照微分数学知识,可以将虎克体与牛顿体的本构关系方程改写为 与
与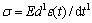 ,由此可以发现:不同的微分阶数(0与1)代表了理想固体与理想流体的变形表征。因此,当微分阶数处于(0 1)区间之间时,即可抽象地理解为上述方程描述的是介于理想固体与理想流体之间的材料介质本构关系[6]。文献[6]将其定义为软体元件,如图2所示。
,由此可以发现:不同的微分阶数(0与1)代表了理想固体与理想流体的变形表征。因此,当微分阶数处于(0 1)区间之间时,即可抽象地理解为上述方程描述的是介于理想固体与理想流体之间的材料介质本构关系[6]。文献[6]将其定义为软体元件,如图2所示。

图2 软体元件
Fig. 2 Soft-matter element
软体元件的本构方程为
 ,0≤
,0≤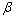 ≤1 (4)
≤1 (4)
式中: 和
和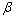 均为材料常数;
均为材料常数; 为分数阶软体元件的类黏滞系数,其物理量纲为[应力·时间β];
为分数阶软体元件的类黏滞系数,其物理量纲为[应力·时间β];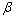 为分数阶软体元件的阶数。
为分数阶软体元件的阶数。
当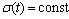 时,软体元件即描述岩土材料的蠕变行为,对式(4)两边进行积分,依据Riemannn- Liouville型分数阶微积分算子理论,可得到软体元件的蠕变方程为
时,软体元件即描述岩土材料的蠕变行为,对式(4)两边进行积分,依据Riemannn- Liouville型分数阶微积分算子理论,可得到软体元件的蠕变方程为
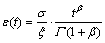 ,0≤
,0≤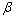 ≤1 (5)
≤1 (5)
通过调节阶数,可以得到不同下凹弯曲程度的蠕变曲线。文献[16]探讨了当阶数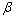 >1时,可以得到不同上凹弯曲程度的类似材料加速蠕变段的曲线。曲线形态与岩土材料加速蠕变段曲线近似度很高,但其数学表示的物理意义有待深入研究。本文以应力
>1时,可以得到不同上凹弯曲程度的类似材料加速蠕变段的曲线。曲线形态与岩土材料加速蠕变段曲线近似度很高,但其数学表示的物理意义有待深入研究。本文以应力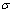 为100 kPa,类黏滞系数
为100 kPa,类黏滞系数 为2 000 kPa·minβ为参考条件,分别计算了当
为2 000 kPa·minβ为参考条件,分别计算了当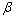 为0.1,0.2,0.3,0.5,0.7,1.0,1.1,1.5,2.5和3.5时蠕变随时间变化值,并得出了不同阶数时的应变时间图,如图3所示。从图3可见:当0<
为0.1,0.2,0.3,0.5,0.7,1.0,1.1,1.5,2.5和3.5时蠕变随时间变化值,并得出了不同阶数时的应变时间图,如图3所示。从图3可见:当0<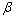 <1时,分数阶微积分软体元件的蠕变曲线可用来描述岩土材料的稳定蠕变,同时经过仔细观察,可以初步判断当0.1≤
<1时,分数阶微积分软体元件的蠕变曲线可用来描述岩土材料的稳定蠕变,同时经过仔细观察,可以初步判断当0.1≤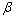 ≤0.5时,软体元件可用以描述黄土的稳定蠕变;当
≤0.5时,软体元件可用以描述黄土的稳定蠕变;当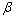 >1时,蠕变曲线形态与黄土加速蠕变段曲线非常相似,但其物理含义无法明确。
>1时,蠕变曲线形态与黄土加速蠕变段曲线非常相似,但其物理含义无法明确。

图3 分数阶微分元件的蠕变曲线
Fig. 3 Creep curves of fractional calculus element
2.3 常参数黄土蠕变模型
根据含水Q2黄土三轴蠕变试验结果表明黄土的变形包括2个部分:一部分为瞬时变形,另一部分为蠕变变形。通常黄土的瞬时变形可用一虎克体弹簧来描述。而对于黄土的蠕变变形,当加载应力小于黄土的某一临界应力时,蠕变变形主要出现减速蠕变与等速蠕变;当加载应力大于黄土的临界应力时,黄土蠕变曲线出现时间短暂的加速蠕变。鉴于其曲线形态所表现的特点,本文尝试用包含软体元件的模型来描述黄土的蠕变变形特征。为全面描述Q2黄土的流变特性,基于分数阶微积分特点,本文采用文献[16]提出的四元件蠕变模型,如图4所示。

图4 常参数黄土蠕变模型
Fig. 4 Constant parameters creep model of loess
由图4的模型结构及连接特性可得到模型的蠕变方程为:
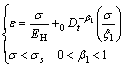 (6)
(6)
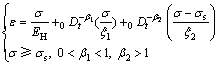 (7)
(7)
对式(6)与式(7)中D(·)采用Riemannn-Liouville型分数阶微积分算子,可得到常参数黄土蠕变方程如下。
当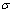 <
<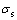 时,
时,
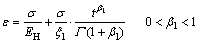 (8)
(8)
当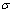 ≥
≥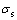 时,
时,
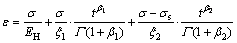
 (9)
(9)
式中:EH为瞬时弹性模量;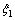 和
和 为类黏滞系数;
为类黏滞系数;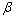 为分数阶微积分阶数。
为分数阶微积分阶数。
上述四元件蠕变模型虽然已借用分数阶软体元件替换了以往的理想流体元件,使得模型从物理意义上更加符合岩土材料的描述,但其类黏滞系数依然作为常数存在。而实践表明,岩土材料大多属于非线性、非均质的各向异性材料。当岩土材料在发生蠕变时,力学性质会随着应力与时间发生变化,相应的黏滞性能也在发生变化。因此,为进一步反映黄土材料流变的非线性特征,模型中的软体元件需要进一步改进。
3 变参数黄土蠕变损伤模型
3.1 对黏弹性部分的改进
对于岩土材料流变非线性的研究,多数学者都是通过修改黏滞元件的参数来实现。变元件模型中黏滞常参数为应力或时间的函数,即 。宋飞等[19]构建了1个SN元件与1个SP元件用以描述石膏角砾岩的非线性蠕变特征及加速蠕变。其中SN元件的本构方程与蠕变方程为
。宋飞等[19]构建了1个SN元件与1个SP元件用以描述石膏角砾岩的非线性蠕变特征及加速蠕变。其中SN元件的本构方程与蠕变方程为
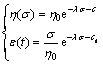 (10)
(10)
应用SN元件改进常参数黄土蠕变模型中黏弹性段中的软体元件,如式(11)所示,改进其类黏滞系数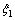 为应力的函数。
为应力的函数。
 (11)
(11)
则变黏性系数软体元件的蠕变方程为
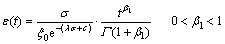 (12)
(12)
3.2 对黏塑性部分的改进
岩土材料属于非均质、非线性的材料。材料内部存在孔隙、空隙及微裂缝等原生缺陷或损伤。当岩土材料受压时,其变形初期主要是因孔隙、空隙的压密以及微裂缝尖端应力集中导致的微开裂。随着应力的增大,微裂缝尖端开裂逐渐壮大、扩展、联合造成更大尺寸的裂缝发展,最终衍生为宏观破裂。上述微裂缝尖端开裂的逐渐壮大、扩展生长为大裂缝进而导致宏观破裂的实质即是岩土材料的损伤加剧恶化的过程。岩土体的流变是岩土材料在一定应力水平的恒定长时间作用下的变形反映。而实践表明,岩土体发生流变会产生内部损伤,但损伤如何发生依然处于讨论阶段。当前,关于岩土材料发生流变如何产生损伤主要有2种观点[13]:一种观点(观点一)倾向于损伤随受载应力实时发生,即损伤不存在应力阈值;另一种观点(观点二)则认为当应力只有大于某临界值(长期强度)时,损伤才会产生。分析众多岩土材料受力后的微观试验观察结果发现,观点一所描述的岩土发生流变时损伤随受力即时发生与众多微观观察结果不符。孙钧[1]认为,在恒温时,无论是宏观损伤试验或者岩土细观观察试验,只有当加载应力高于临界阈值时,岩土的时效损伤才会产生。因此,基于损伤原理构建包含蠕变损伤变量的岩土流变模型时考虑损伤的应力门槛原则是基本合理的。黄土作为一种亲水性强的土体材料,遇水之后土粒之间的干燥连接被水破坏,在应力作用下,损伤因此被加剧,而且水体的此种辅助损伤加剧随着含水率增大而增大。结合文献[13]和[20]的研究,按照能量损伤原理,考虑应力、时间及含水的损伤变量可定义为:
 (13)
(13)
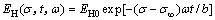 (14)
(14)
式中:EH0为初始弹性模量;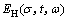 为任意时刻、任意状态时材料弹性模量;
为任意时刻、任意状态时材料弹性模量; 为长期强度;b为材料常数;
为长期强度;b为材料常数;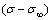 为开关函数,其形式为
为开关函数,其形式为
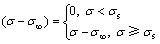 (15)
(15)
将式(15)代入式(14),得其损伤演化方程为
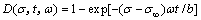 (16)
(16)
前述常参数黄土蠕变模型黏塑性段本构方程为
 (17)
(17)
按照应变等效原理,将式(16)代入上述黄土蠕变模型黏塑性体本构方程中得
 (18)
(18)
求解上述微分方程(采用R-L型微积分算子)得改进前述黄土蠕变模型黏塑性体蠕变方程为
 (19)
(19)
3.3 变参数黄土蠕变损伤模型
综合考虑改进后的黄土蠕变模型弹性、黏滞性及黏塑性部分蠕变,得变参数黄土蠕变损伤模型如图5所示。
依照模型连接特性及结构特征,其整体蠕变方程如下。
当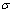 <
<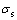 时,
时,
 (20)
(20)
当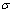 ≥
≥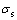 时,
时,
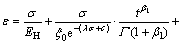
 (21)
(21)
式中:EH为弹性模量;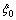 和
和 为软体元件的类黏滞系数;
为软体元件的类黏滞系数; ,c和b为材料常数;
,c和b为材料常数;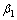 和
和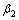 为软体元件的微积分阶数。
为软体元件的微积分阶数。
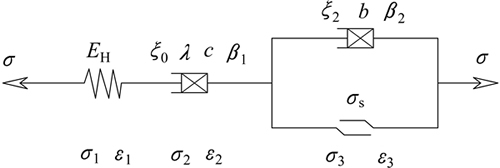
图5 变参数黄土蠕变损伤模型
Fig. 5 Variable parameters creep damage model of loess
4 模型验证
如式(20)与式(21)所示,变参数黄土蠕变损伤模型包含EH,ξ0,λ,c,β1,ξ2,b和β2 这8个参数。根据前期进行的不同含水率Q2黄土蠕变试验结果,应用1stOpt数学软件采用麦夸特法(Levenberg-Marquardt)对变参数黄土蠕变损伤模型进行拟合。本文仅给出含水率8%下Q2黄土蠕变拟合结果。表1所示为含水率8%下的Q2黄土蠕变试验结果对变参数黄土蠕变损伤模型弹性、黏弹性段拟合参数值,当加载应力为518 kPa(大于临界应力)时,模型黏塑性段发挥作用,描述黄土非线性加速蠕变特征,此时其ξ2为5 984.38 kPa·minβ2、b为2 362.36,β2为1.873。图6所示为模型理论值与试验值的对比结果。可观察分析图6得到:基于分数阶微积分及损伤原理构建的变参数黄土蠕变损伤模型可以很好地反映Q2黄土的整体流变特性。
表1 变参数黄土蠕变损伤模型参数(ω=8%)
Table 1 Parameters of variable parameters creep damage model of loess (ω=8%)


图6 含水率8%试样蠕变试验值与理论值
Fig. 6 Creep trial value and theoretic value of specimens whose moisture content is 8%
5 结论
1) 不同含水率Q2黄土三轴蠕变试验结果表明,含水率的增高伴随着黄土流变性能的增强。
2) 基于分数阶微积分构建的软体元件相比传统的牛顿黏滞元件,能够更加真实地反映介于理想固体与理想流体之间的岩土材料的流变特性。
3) 应用SN元件改进常参数软体元件得到的变参数软体元件可以反映岩土材料随应力变化的流变非线性特征。引入反映应力水平、时间及含水率影响的损伤变量可以反映岩土材料的流变损伤特征。
4) 基于变参数软体元件构建的四元件蠕变损伤模型经过黄土蠕变试验数据的验证,可以有效描述Q2黄土的整体流变。
参考文献:
[1] 孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999: 3-4, 400-401.
SUN Jun. Rheology of geo-material and its engineering application[M]. Beijing: China Architecture and Building Press, 1999: 3-4, 400-401.
[2] 郭增玉, 张朝鹏, 夏旺民. 高湿度Q2黄土的非线性流变本构模型及参数[J]. 岩石力学与工程学报, 2000, 19(6): 780-784.
GUO Zenyu, ZHANG Chaopeng, XIA Wangmin. Nonlinear rheological constitutive models and their parameters of high moisture Q2 loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(6): 780-784.
[3] 朱才辉, 李宁, 刘俊平. 压实Q3马兰黄土蠕变规律研究[J]. 西安理工大学学报, 2011, 27(4): 392-399.
ZHU Caihui, LI Ning, LIU Junping. Research on the creep behavior of compacted Q3 Malan loess[J]. Journal of Xi’an University of Technology, 2011, 27(4): 392-399.
[4] 谢星, 王东红, 赵法锁. Q2黄土流变特性及其统计损伤流变模型[J]. 水文地质工程地质, 2010, 37(3): 63-68.
XIE Xing, WANG Donghong, ZHAO Fasuo. Study on rheological properties and statistical damage rheological model for Q2 loess[J]. Hydrogeology & Engineering Geology, 2010, 37(3): 63-68.
[5] 王东红, 谢星, 赵法锁. 考虑蠕变损伤的Q2黄土流变本构模型[J]. 西安科技大学学报, 2010, 30(6): 682-686.
WANG Donghong, XIE Xing, ZHAO Fasuo. Creep damage rheological constitutional model for Q2 loess[J]. Journal of Xi’an University of Science and Technology, 2010, 30(6): 682-686.
[6] 殷德顺, 任俊娟, 和成亮, 等. 一种新的岩土流变模型元件[J]. 岩石力学与工程学报, 2007, 26(9): 1989-1903.
YING Deshun, REN Junjuan, HE Chenliang, et al. A new rheological model element for geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1989-1903.
[7] 郭佳奇, 乔春生, 徐冲, 等. 基于分数阶微积分的Kelvin-Voigt流变模型[J]. 中国铁道科学, 2009, 30(4): 1-6.
GUO Jiaqi, QIAO Chunsheng, XU Chong, et al. The Kelvin-Voigt rheological model based on fractional calculus[J]. China Railway Science, 2009, 30(4): 1-6.
[8] 孙海忠, 张卫. 一种分析软土黏弹性的分数导数开尔文模型[J]. 岩土力学, 2007, 28(9): 1983-1986.
SUN Haizhong, ZHANG Wei. Analysis of soft soil with viscoelastic fractional derivative Kelvin model[J]. Rock and Soil Mechanics, 2007, 28(9): 1983-1986.
[9] 丁靖洋, 周宏伟, 李潮, 等. 基于Weibull分布的盐岩分数阶蠕变本构模型研究[J]. 固体力学学报, 2013, 34(5): 479-480.
DING Jingyang, ZHOU Hongwei, LI Chao, et al. The fractional derivative approach to creep constitutive model of salt rock based on Weibull distribution[J]. Chinese Journal of Solid Mechanics, 2013, 34(5): 479-480.
[10] 周宏伟, 王春萍, 段志强, 等. 基于分数阶导数的盐岩流变本构模型[J]. 中国科学: 物理学 力学 天文学, 2012, 42(3): 310-318.
ZHOU Hongwei, WANG Chunping, DUAN Zhiqiang et al. time-based fractional derivative approach to creep constitutive model of salt rock[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2012, 42(3): 310-318.
[11] Welch S W J, Rorrer R A L, Duren Jr R G. Application of time-based fractional calculus methods to viscoelastic creep and stress relaxation of materials[J]. Mechanics of Time-Dependent Materials, 1999, 3(3): 279-303.
[12] Adolfsson K, Ennelund M, Olsson P. On the fractional order model of viscoelasticity[J]. Mechanics of Time-Dependent Materials, 2005, 9(1): 15-34.
[13] 宋勇军, 雷胜友. 基于分数阶微积分的岩石非线性蠕变损伤力学模型[J]. 地下空间与工程学报, 2013, 9(1): 91-95.
SONG Yongjun, LEI Shengyou. Mechanical model of rock nonlinear creep damage based on fractional calculus[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(1): 91-95.
[14] 宋勇军, 雷胜友, 韩铁林. 一种新的岩石非线性黏弹塑性流变模型[J]. 岩土力学, 2012, 33(7): 2076-2080.
SONG Yongjun, LEI Shengyou, HAN Tielin. A new nonlinear viscoelasto-plastic rheological model for rocks[J]. Rock and Soil Mechanics, 2012, 33(7): 2076-2080.
[15] 陈军浩, 姚兆明, 徐颖, 等. 人工冻土蠕变特性粒子群分数阶导数模型[J]. 煤炭学报, 2013, 38(10): 1763-1768.
CHEN Junhao, YAO Zhaoming, XU Ying, et al. Particle swarm fractional order derivative model of artificial frozen soil creep properties[J]. Journal of China Coal Society, 2013, 38(10): 1763-1768.
[16] 陈亮, 陈寿根, 张恒, 等. 基于分数阶微积分的非线性黏弹塑性蠕变模型[J]. 四川大学学报(工程科学版), 2013, 45(3): 7-11.
CHEN Liang, CHEN Shougeng, ZANG Heng, et al. A nonlinear viscoelasto-plastic creep model based on fractional Calculus[J]. Journal of Sichuan University (Engineering Science Edition), 2013, 45(3): 7-11.
[17] Beda T, Chevalier Y. New methods for identifying rheological parameter for fractional derivative modeling of viscoelastic behavior[J]. Mechanics of Time-Dependent Materials, 2004, 8(2): 105-118.
[18] 黎明. 分数阶微积分及其在黏弹性材料与核磁共振中的某些应用[D]. 济南: 山东大学数学学院, 2013: 1-7.
LI Ming. Fractional calculus and its application to viscoelastic materials and nuclear magnetic resonance[D]. Tsinan: Shandong University. School of Mathematics, 2013: 1-7.
[19] 宋飞, 赵法锁, 卢全中. 石膏角砾岩流变特性及流变模型研究[J]. 岩石力学与工程学报, 2005, 24(15): 2659-2664.
SONG Fei, ZHAO Fasuo, LU Quanzhong. Study on rheological properties and model for gypsum breccias[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2659-2664.
[20] 刘保国, 崔少东. 泥岩蠕变损伤试验研究[J]. 岩石力学与工程学报, 2010, 29(10): 2127-2133.
LIU Baoguo, CUI Shaodong. Experimental study of creep damage of mudstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 2127-2133.
(编辑 罗金花)
收稿日期:2014-12-07;修回日期:2015-02-07
基金项目(Foundation item):中央高校基本科研业务费专项资金资助项目(CHD2010JC118);国家自然科学基金资助项目(40872185) (Project(CHD2010JC118) supported by the Fundamental Research Funds for the Central Universities; Project(40872185) supported by the National Natural Science Foundation of China)
通信作者:王东坡,博士,讲师,从事山地灾害机制研究;E-mail: dongpo_007@163.com