基于响应面法的Inconel 625合金大型厚壁管挤压加工窗口确定
来源期刊:中国有色金属学报(英文版)2016年第7期
论文作者:郭良刚 党利 杨合 张君 郑文达
文章页码:1902 - 1911
关键词:型材挤压;加工窗口;响应面法;难变形材料;有限元模拟
Key words:profile extrusion; processing window; response surface methodology; difficult-to-deform materials; finite element simulation
摘 要:研究确定难变形Inconel 625合金大型厚壁管挤压加工窗口,是获得具有良好组织性能挤压管材的关键。采用响应面法建立了一种确定基于温控挤压加工窗口的方法。首先,采用基于有限元计算数据的正交回归方法,建立了分别描述温升和峰值温度与关键挤压参数之间的响应面模型;其次,基于建立的响应面模型,分析揭示了关键挤压参数对温升和温度峰值的交互作用规律;最后,通过绘制挤压速度和初始温度空间峰值温度的等高线图,建立了不同挤压比下挤压加工窗口。基于该挤压加工窗口,可方便快速地确定合适的关键挤压参数组合。
Abstract: Identifying suitable processing window is necessary but difficult for achieving favorable microstructure and performance in extrusion of large thick-walled pipe with difficult-to-deform Inconel 625 alloy. In this work, a method was established for identifying the extrusion process window considering temperature control using response surface methodology. Firstly, the response surface models, which correlate temperature rise and peak temperature to key extrusion parameters, have been developed by orthogonal regression based on finite element calculated data. Secondly, the coupled effects of the key extrusion parameters on the temperature rise and peak temperature have been disclosed based on the regression models. Lastly, suitable extrusion processing windows, which are described by contour map of peak temperature in the space of extrusion speed and initial billet temperature, have been established for different extrusion ratios. Using the identified process window, a suitable combination of the key extrusion parameters can be determined conveniently and quickly.
Trans. Nonferrous Met. Soc. China 26(2016) 1902-1911
Liang-gang Guo1, Li Dang1, He Yang1, Jun Zhang2, Wen-da Zheng2
1. State Key Laboratory of Solidification Processing, School of Materials Sciences and Engineering, Northwestern Polytechnical University, Xi’an 710072, China;
2. China National Heavy Machinery Research Institute Co., Ltd., Xi’an 710032, China
Received 18 June 2015; accepted 13 October 2015
Abstract: Identifying suitable processing window is necessary but difficult for achieving favorable microstructure and performance in extrusion of large thick-walled pipe with difficult-to-deform Inconel 625 alloy. In this work, a method was established for identifying the extrusion process window considering temperature control using response surface methodology. Firstly, the response surface models, which correlate temperature rise and peak temperature to key extrusion parameters, have been developed by orthogonal regression based on finite element calculated data. Secondly, the coupled effects of the key extrusion parameters on the temperature rise and peak temperature have been disclosed based on the regression models. Lastly, suitable extrusion processing windows, which are described by contour map of peak temperature in the space of extrusion speed and initial billet temperature, have been established for different extrusion ratios. Using the identified process window, a suitable combination of the key extrusion parameters can be determined conveniently and quickly.
Key words: profile extrusion; processing window; response surface methodology; difficult-to-deform materials; finite element simulation
1 Introduction
The large thick-walled Inconel 625 alloy pipe is widely employed in aerospace, nuclear power plant, and oil and chemistry industries due to its preferable heat resistance, high strength and ductility, favorable fatigue and corrosion resistance [1-3]. The extrusion process is an advanced manufacture technology for the large thick- walled superalloy pipes because of its many technical advantages, such as obtaining fine microstructure, higher efficiency, saving materials and lower cost [4,5]. However, due to high extrusion speed, extrusion ratio and deformation resistance in extrusion of large thick- walled pipe (ELTP) with Inconel 625 alloy, local drastic temperature rise often occurs, consequently resulting in local coarse grain and non-uniform microstructure of the extruded pipe. Thus, the temperature effect is one of the most important concerns for controlling the microstructure and performance in ELTP with difficult-to-deform materials.
Thus, many researchers focused their attention on the temperature evolution in the pipe extrusion process of difficult-to-deform alloy. For example, Guo and YANG [6] revealed the influence rules of key extrusion parameters on peak temperature in extrusion of large thick-walled Inconel 690 pipes. Liu et al [7] predicted the variation of the exit temperature with the initial billet temperature during extrusion of an AZ31 profile. JianG et al [8] studied the temperature rise in CP-Ti during equal channel angular extrusion by finite element analysis. Li et al [9] studied the temperature distribution in the extrusion process of Ti-6Al-4V alloy. MIRAHMADI and HAMEDI [10] analyzed the effects of key extrusion parameters on peak temperature in extrusion of Ti-6Al-4V alloy bar. But in summary, the above studies mainly considered the effects of single extrusion parameter on temperature in the process. In other words, the complex interactive influences of various key extrusion parameters on temperature evolution are rarely discussed in the above investigations. Therefore, it is difficult to quickly plan the extrusion process through finding a suitable combination of various key extrusion parameters.
However, huge amounts of data are needed in order to reveal the complex interactive influences of various key extrusion parameters on temperature in ELTP. It is impractical and unnecessary to get the huge amounts of data by actual physical experiments due to high cost, long period, etc. Finite element simulation of the process is a practical and feasible way for solving the above problem. But a large number of computational costs are needed for simulation of ELTP [11]. Response surface methodology (RSM) is a combination of mathematical and statistical techniques [12]. It usually can be used to develop mathematical model correlating a response to several independent variables in a process and to control or optimize the response based on minimum number of real physical experiments or virtual simulation experiments [13]. So, the minimum number of calculation cost is needed to reveal the interactive influences of various key extrusion parameters on temperature in ELTP by RSM in conjunction with FE simulations.
In view of the above consideration, the extrusion process of a large thick-walled Inconel 625 alloy pipe with sizes of d300 mm × 50 mm × 6000 mm has been investigated by using RSM in conjunction with FE analysis in this work. The expected aims of the work are: to develop response surface models respectively correlating temperature rise and peak temperature to key extrusion parameters based on the virtual orthogonal simulation experiments of the process; to mainly reveal the coupled effects of the key extrusion parameters on the temperature evolution in the process based on the developed response surface models; and to find the processing windows considering temperature control in the space of initial billet temperature and extrusion speed under different extrusion ratio for quick process design and optimization.
2 Experimental
Inconel 625 alloy is a difficult-to-deform material because of its pretty narrow forming window. Temperature is one of the most important factors for controlling the microstructure and performance in extrusion of large thick-walled Inconel 625 alloy pipe. But due to complex interactive influences of key extrusion parameters on temperature, identifying suitable processing window considering temperature control is difficult. Thus, in this work, a method for identifying the extrusion process window considering temperature control using response surface methodology (RSM) is proposed.
There are two important temperature parameters for the control of the microstructure and performance of the extruded pipe. One is the peak temperature denoted by Tmax in the extrusion process, another is the temperature rise Trise which is defined as Trise=Tmax-T0, T0 is the initial billet temperature. In this work, the response surface models respectively correlating Trise and Tmax to key extrusion parameters, namely the initial billet temperature T0, extrusion speed v and extrusion ratio λ, are developed using virtual orthogonal FE simulation experiments. So, the first step for developing the response surface models is to build a thermal-mechanical coupled FE model for the extrusion process.
2.1 Thermal-mechanical coupled finite element model
Figure 1(a) shows the extrusion principle of large thick-walled Inconel 625 pipe and the die structure diagram. Based on the extrusion principle, a thermal- mechanical coupled FE model for the process of ELTP with Inconel 625 alloy was developed under DEFORM software environment in Ref. [14], as shown in Fig. 1(b).
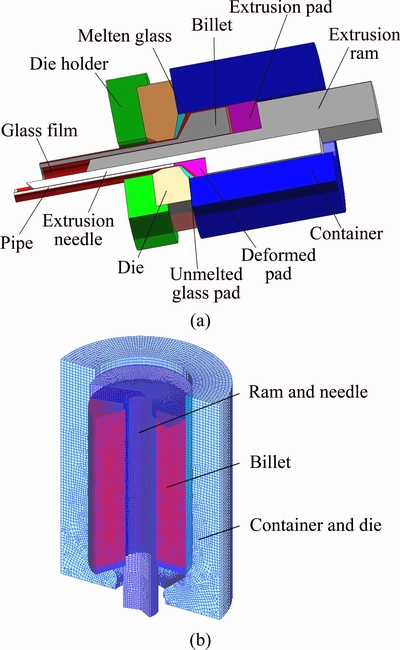
Fig. 1 Extrusion principle (a) and FE model (b) of extrusion process of large thick-walled Inconel 625 pipe
In summary, the main technical details of the developed FE model for ELTP with Inconel 625 alloy are as follows.
1) A 2D axisymmetrical model has been developed in consideration of geometry symmetry of the extrusion billet and dies. The billet and dies are meshed using quadrilateral elements. The local mesh refinement in the deformation zone is conducted in order to improve computational accuracy and efficiency. And the adaptive remeshing technology is employed to avoid mesh distortion.
2) The thermal-mechanical coupled deformation behavior data of Inconel 625 alloy from Refs. [15-17], such as true stress-strain curves, thermal conductivity, specific heat, are used in the model. And the model can calculate temperature change of the billet when transferring from furnace to the extruder for accurate prediction of deformation and temperature. The details can be seen in Ref. [14].
3) The key extrusion parameters ranges T0= 1000-1200 °C, v=100-200 mm/s, and λ=4-7 are selected according to Ref. [18]. Therefore, the process boundary conditions of the model can be determined. The heat boundary conditions of the model also can be seen in Ref. [14]. And the reliability of the model has been verified in terms of extrusion load based on the experimental data in Ref. [19].
2.2 Virtual orthogonal experiments
After developing the thermal-mechanical coupled FE model, the second step for establishing response surface models of Tmax and Trise is to obtain their response data to various combinations of key extrusion parameters through FE simulations. In general, the response surface model can be developed by uniform experimental design, orthogonal experimental design, central composite experimental design, and so on [20]. In current study, the virtual orthogonal experimental design based on FE simulation is used to develop the response surface models of Tmax and Trise.
Table 1 gives the actual and coded levels of the key extrusion parameters used to virtual orthogonal experiment design. The levels of the key extrusion parameters are selected in their reasonable ranges as mentioned above (T0=1000-1200 °C, v=100-200 mm/s, and λ=4-7). The orthogonally coded levels of the key extrusion parameters are calculated by Eq. (1), in which, Amax and Amin are the maximum and minimum levels of each extrusion parameter, respectively; Ai is the ith level of each extrusion parameter; x1, x2 and x3 are the coded levels of the initial billet temperature T0, extrusion speed v and extrusion ratio λ, respectively.
 (1)
(1)
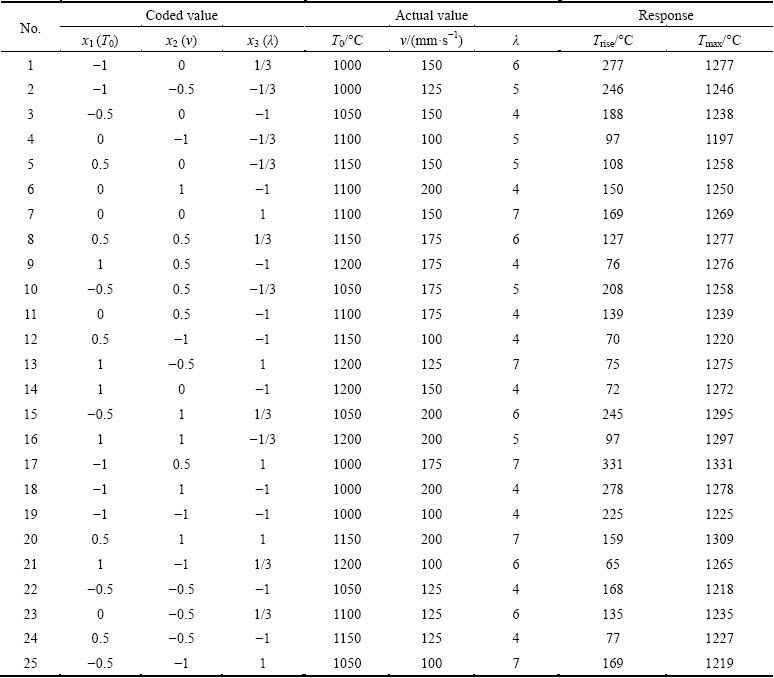
Table 2 shows the orthogonal layout for virtual FE simulation experiments. There are twenty-five combinations of the key extrusion parameters for the FE simulation experiments. So, twenty-five FE models are built and calculated. For each combination of the key extrusion parameters, the calculated responses of temperature rise Trise and peak temperature Tmax are also listed in the Table 2 accordingly.
2.3 Response surface models
The response surface models are orthogonally regressed using a second order polynomial function with three independent variables x1, x2, and x3, as expressed by Eq. (2), where a0 is the average response and ai (i=1-9) are the response coefficients, Y is the response variable.
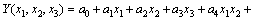
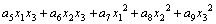 (2)
(2)
Using the data in Table 2, the response surface models of Trise and Tmax in terms of coded factors, expressed by Eqs. (3) and (4), have been fitted using stepwise regression method for the improvement of predictive accuracy under Design-Expert software environment. And the corresponding response surface models in terms of actual factors are expressed by Eqs. (5) and (6).
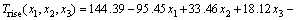
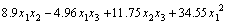 (3)
(3)

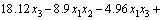
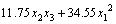 (4)
(4)
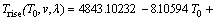

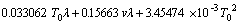 (5)
(5)


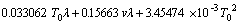 (6)
(6)
In order to evaluate the regression models of Trise and Tmax, the analysis of variance (ANOVA) is carried out. And the ANOVA test results for Trise and Tmax models are shown in Table 3 and Table 4, respectively. The model F-values of 608.88 and 107.35 imply that the models are significant. The high adjusted determination coefficient (Adj R2) also indicates that the models are significant. Values of “Prob > F” less than 0.05 indicate that the model terms are significant. In this case, x1, x2, x3, x1x2, x1x3, x2x3, x12 are significant model terms. The predicted values of R2 (Pred R2) are in reasonable agreement with the adjusted R2 (Adj R2).
Table 1 Actual and coded levels of key extrusion parameters used to virtual orthogonal experiment design
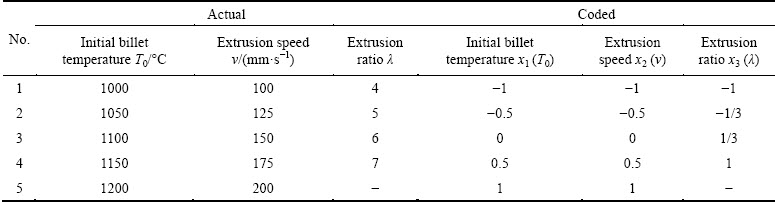
Table 2 Virtual orthogonal experiment layout and calculated responses of Tmax and Trise by FE simulations
The values of R2 for the developed Trise and Tmax models are found to be above 0.95, which indicates high correlation between the simulated values and the predicted values. Figure 2 also shows the high correlation between the simulated values and the predicted values.
To further verify the reliability of the developed response surface models, five random selected extrusion processes, as listed in Table 5, are simulated by FE calculation. The simulated and predicted values of Trise and Tmax show that the developed response surface models can precisely describe the relationships between the responses (Trise and Tmax) and the key extrusion parameters (T0, v and λ), as shown in Table 5.
Table 3 ANOVA test results for temperature rise model
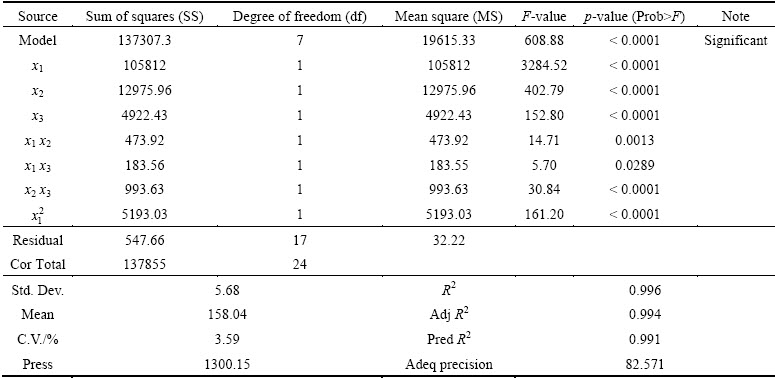
Table 4 ANOVA test results for peak temperature model
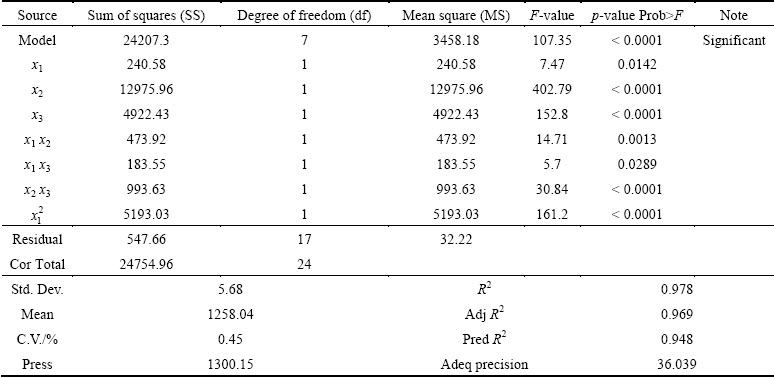
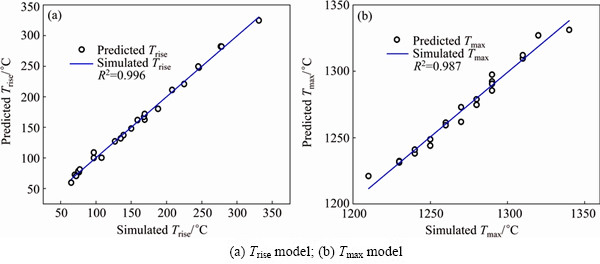
Fig. 2 Correlation graphs between simulated values and predicted values
Table 5 FE calculation conditions and simulated and predicted Trise and Tmax

3 Results and discussion
3.1 Effects of key extrusion parameters on temperature
Based on the above developed response surface models of Trise and Tmax correlating to the key extrusion parameters (T0, v and λ), the single-factor effects and coupled effects of the key extrusion parameters on Trise and Tmax can be disclosed explicitly. When arbitrary two of the key extrusion parameters are determined, the single-factor effects of the left one parameter on the temperature evolution can be revealed. And when one of the key extrusion parameters is given, then the coupled effects of the left two parameters on the temperature evolution can be disclosed.
3.1.1 Single-factor effects
Figure 3 gives the single-factor effects of the initial billet temperature T0 on Tmax and Trise when v=150 mm/s and λ=6. It can be seen that Trise gradually decreases with the increase of T0. This is because the deformation heat and friction heat all will reduce due to the decline of deformation resistance when T0 increases. We can also see that Tmax first decreases and then increases with increasing T0. This is because Tmax is the sum of decreasing Trise and increasing T0, as shown in Fig. 3.
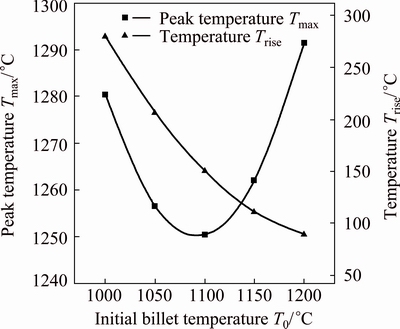
Fig. 3 Single-factor effects of initial billet temperature T0 on Trise and Tmax
Figure 4 shows the single-factor effects of the extrusion speed v on Tmax and Trise when T0=1100 °C and λ=6. Trise and Tmax rapidly linearly increase with increasing the extrusion speed. This is reasonable because deformation heat and friction heat all will increase due to larger deformation resistance resulting from increasing deformation rate for high extrusion speed v.
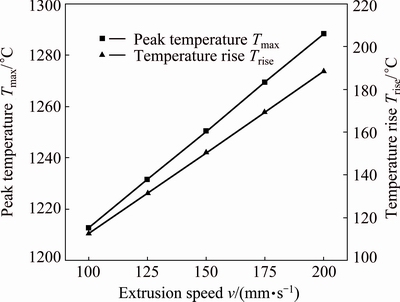
Fig. 4 Single-factor effects of extrusion speed v on Trise and Tmax
Figure 5 shows the single-factor effects of the extrusion ratio λ on Tmax and Trise when T0=1100 °C and v=150 mm/s. We can see that Trise and Tmax slowly linearly increase with the increase of λ due to larger deformation heat and friction heat resulting from larger deformation degree for large extrusion ratio λ.
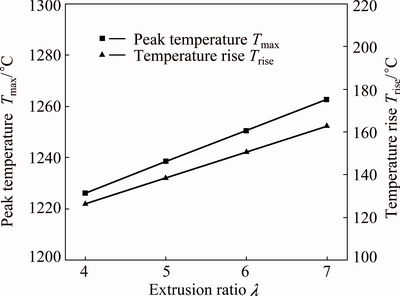
Fig. 5 Single-factor effects of extrusion ratio λ on Trise and Tmax
3.1.2 Coupled effects
The coupled effects of any two of the key extrusion parameters on Trise and Tmax can be described by plotting the response surface of the developed response surface models. The calculation conditions for plotting the response surfaces are as follows:
1) To reveal interactive effects of T0 and v on Trise and Tmax, the corresponding calculation condition is λ=6, T0 and v change in their ranges of T0 = [1000, 1050, 1100, 1150, 1200] °C and v=[100, 125, 150, 175, 200] mm/s, respectively.
2) To reveal interactive effects of λ and v on Trise and Tmax, the corresponding calculation condition is T0=1100 °C, λ and v change in their ranges of λ=[4, 5, 6, 7] and v =[100, 125, 150, 175, 200] mm/s, respectively.
3) To reveal interactive effects of T0 and λ on Trise and Tmax, the corresponding calculation condition is v=150 mm/s, T0 and λ change in their ranges of T0=[1000, 1050, 1100, 1150, 1200] °C and λ= [4, 5, 6, 7], respectively.
Based on the developed response surface model of Trise and above calculation conditions, the response surfaces of Trise to T0 and v (a), λ and v (b), and T0 and λ (c) have been plotted as shown in Fig. 6. From Fig. 6(a), we can see that a combination of the highest T0 and the smallest v will lead to the smallest Trise for a given λ, and vice versa. It can be seen from Fig. 6(b) that a combination of the smallest λ and the smallest v will lead to the smallest Trise for a given T0, and vice versa. And from Fig. 6(c), it can be seen that a combination of the highest T0 and the smallest λ will lead to the smallest Trise for a given v, and vice versa. So, the response surfaces of Trise to T0 and v (a), λ and v (b), and T0 and λ (c) provide a guideline for choosing an appropriate combination of the key extrusion parameters in terms of the change of Trise during the extrusion process.
Based on the developed response surface model of Tmax and above calculation conditions, the response surfaces of Tmax to T0 and v (a), λ and v (b), and T0 and λ (c) have been plotted as shown in Fig. 7. From Fig. 7(a), it can bee seen that a combination of a middle value of T0 and the smallest v will lead to the smallest Tmax for a given λ. From Fig. 7(b), we can observe that a combination of the smallest λ and the smallest v will lead to the smallest Tmax for a given T0, and vice versa. And from Fig. 7(c), it can be seen that a combination of a middle value of T0 and the smallest λ will lead to the smallest Tmax for a given v. So, the response surfaces of Tmax to T0 and v (a), λ and v (b), and T0 and λ (c) provide a guideline for choosing an proper combination of the key extrusion parameters in terms of the change of Tmax during the extrusion process.
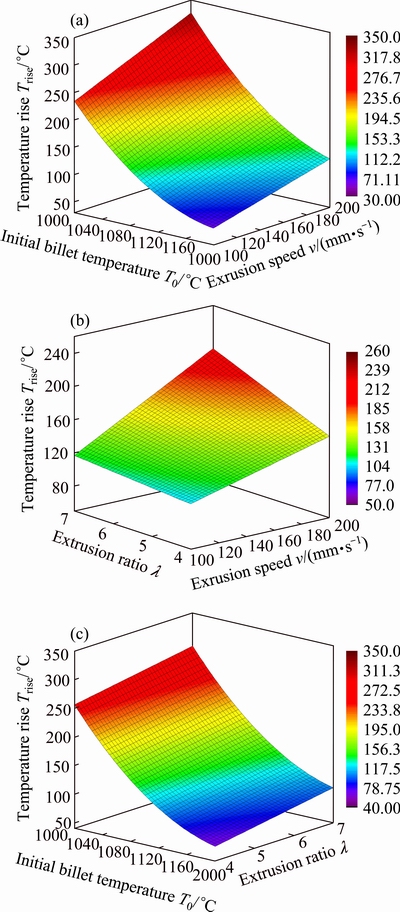
Fig. 6 Response surfaces of Trise to T0 and v (a), λ and v (b), T0 and λ (c)
3.2 Identifying processing window considering temperature control
As discussed above, temperature effect is one of the most important concerns for controlling the microstructure and performance in ELTP with difficult- to-deform Inconel 625 alloys. So, finding processing window based on temperature control is pretty beneficial to quick design and optimization of the process. But the first step is to find the allowable peak temperature in the process of ELTP with Inconel 625 alloys.
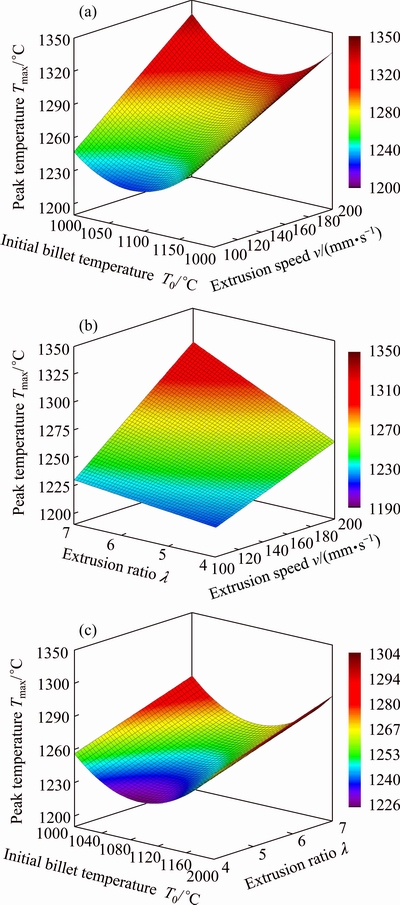
Fig. 7 Response surfaces of Tmax to T0 and v (a), λ and v (b), T0 and λ (c)
Yan [15] investigated high-temperature and high-speed hot deformation behavior of Inconel 625 alloy by hot compression tests. The results show that fully dynamic recrystallization occurs when the samples are deformed at 1200 °C and the grain starts growing, but the grain size is fine enough. Thus, the temperature of 1200 °C can be regarded as limiting hot deformation temperature for obtaining favorable microstructure. However, due to the high strain rate and low heat conductivity of Inconel 625 alloy, temperature rise occurs due to deformation heat in compression tests. In fact, the temperature in the deforming samples is higher than 1200 °C. So, the limiting hot deformation temperature should be higher than 1200 °C.
Based on the above consideration, the temperature rise due to deformation heat is calculated by using Eq. (7) [21] in order to find the true limiting hot deformation temperature.
 (7)
(7)
where △T is the temperature rise, η is the transformation factor from deformation work to thermal energy, σ is the true stress, ε is the true strain, ρ is the material density, cV is the specific heat capacity. For Inconel 625 alloy, η is 0.9, cV is 659 J/(kg·K) and ρ is 8.44 g/cm3. According to the stress-strain curve under the conditions of T0=1200 °C,  =50 s-1 and ε=0.9, the calculated temperature rise is about △T=40 °C. So, the true limiting hot deformation temperature can be regarded as about 1240 °C.
=50 s-1 and ε=0.9, the calculated temperature rise is about △T=40 °C. So, the true limiting hot deformation temperature can be regarded as about 1240 °C.
So, in this work, the peak temperature in ELTP with Inconel 625 alloy is constrained to be lower than 1240 °C for controlling the microstructure and performance of the extruded pipe. And according to the developed response surface model of peak temperature, the response surface of peak temperature to the initial billet temperature and extrusion speed can be plotted for a given extrusion ratio. Therefore, the processing window of ELTP with Inconel 625 alloy, which is described by contour map of peak temperature in the space of the initial billet temperature and extrusion speed, has been determined for each extrusion ratio of λ=[4, 5, 6, 7], respectively, as shown in Fig. 8.
From Fig. 8, we can observe that the larger the extrusion ratio is, the narrower the processing window is. This can be easily understood according to the coupled effects of the key extrusion parameters on the peak temperature as discussed above.
3.3 Discussion on processing window
Using the processing window, we can quickly find a combination of the key extrusion parameters to ensure the peak temperature to be lower than 1240 °C for the control of the microstructure and performance of the extruded pipe. For example, in the case of λ=4, the determined processing window is shown in Fig. 8(a). If we select the initial billet temperature as 1050 °C, then the extrusion speed can be selected in an approximate range of 100-171 mm/s. And if we want to limit the peak temperature to be equal to 1230 °C, then the extrusion speed is about 151 mm/s, as shown in Fig. 8(a). The corresponding combination of the key extrusion parameters is λ=4, T0=1050 °C and v=151 mm/s which is obtained conveniently and quickly.
Although Fig. 8 only gives the processing windows for extrusion ratio λ=4, 5, 6 and 7, in fact, the processing window for any extrusion ratio can be plotted in the space of the initial billet temperature and extrusion speed based on the response surface model of the peak temperature. So, the work carried out in this work provides a convenient guideline for the quick design and optimization of the process of ELTP with difficult-to- deform Inconel 625 alloy.
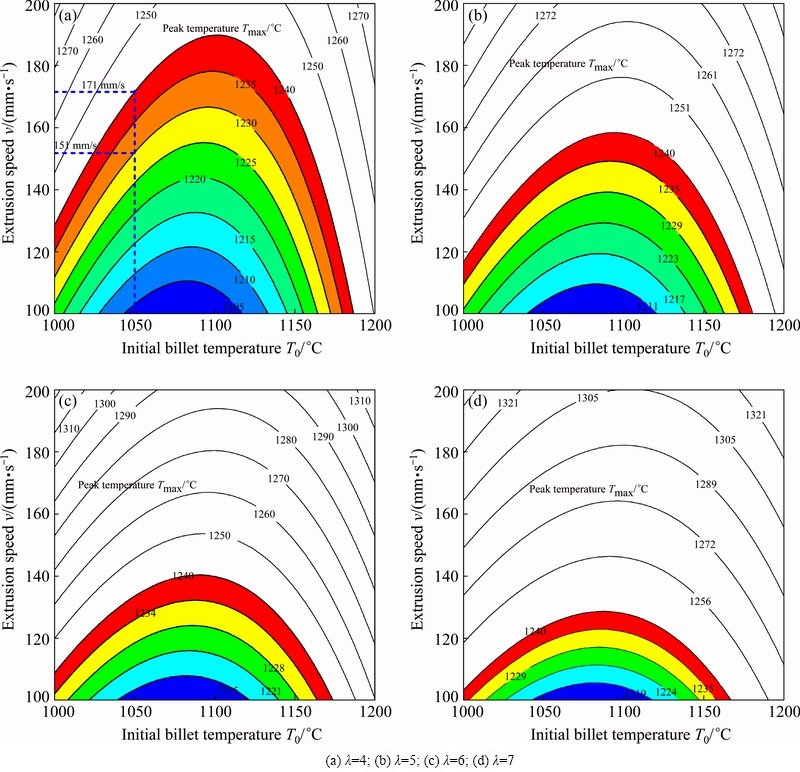
Fig. 8 Processing windows based on peak temperature control for ELTP with difficult-to-deform Inconel 625 under different extrusion ratios
4 Conclusions
1) The response surface models, which respectively correlate the temperature rise and peak temperature to the key extrusion parameters of ELTP with Inconel 625 alloy, have been developed by orthogonal regression analysis based on the calculated data from thermal- mechanical coupled finite element simulations.
2) The response surfaces of the developed models of temperature rise and peak temperature have revealed the coupled effects of any two of the key extrusion parameters on temperature in ELTP with Inconel 625 alloy, which provide a clear direction for choosing an adequate combination of the key extrusion parameters in terms of the temperature change in the process.
3) The suitable processing windows of ELTP with difficult-to-deform Inconel 625 alloy, which are depicted by contour map of peak temperature in the space of initial billet temperature and extrusion speed, have been determined for different extrusion ratios. The work establishes a guideline for quick process design and optimization of ELTP with Inconel 625 alloy.
References
[1] SHANKAR V, BHANU SANKARA RAO K, MANNAN S L. Microstructure and mechanical properties of Inconel 625 superalloy [J]. Journal of Nuclear Materials, 2001, 288: 222-232.
[2] RAI S K, KUMAR A, SHANKAR V, JAYAKUMAR T, Bhanu Sankara Rao K, Raj B. Characterization of microstructures in Inconel 625 using X-ray diffraction peak broadening and lattice parameter measurements [J]. Scripta Materialia, 2004, 51: 59-63.
[3] Guo Jian-ting. The current situation of application and development of superalloys in the fields of energy industry [J]. Acta Metallurgica Sinica, 2010, 46: 513-527.
[4] Zhang Shi-hong, Wang Zhong-tang, Qiao Bing, Xu Yi, Xu Ting-feng. Processing and microstructural evolution of superalloy Inconel 718 during hot tube extrusion [J]. Journal of Materials Science & Technology, 2005, 21: 175-178.
[5] Su Cheng, Zhou Zhi-jiang. Preparation of high-performance stainless pipes and tubes by hot extrusion [J]. Journal of University of Science and Technology Beijing, 2012, 34: 17-20.
[6] Guo Liang-gang, Yang He. Deformation rules and mechanism of large-scale profiles extrusion of difficult-to-deform materials [M]// Comprehensive Materials Processing. Italy: Elsevier, 2014.
[7] Liu G, Zhou J, Duszczyk J. Predicting the variation of the exit temperature with the initial billet temperature during extrusion to produce an AZ31 profile [J]. International Journal of Material Forming, 2009, 2: 113-119.
[8] Jiang Hong, Fan Zhi-guo, Xie Chao-ying. Finite element analysis of temperature rise in CP-Ti during equal channel angular extrusion [J]. Materials Science and Engineering A, 2009, 513-514: 109-114.
[9] Li L X, Rao K P, Lou Y, Peng D S. A study on hot extrusion of Ti-6Al-4V using simulations and experiments [J]. International Journal of Mechanical Sciences, 2002, 44: 2415-2425.
[10] Mirahmadi S J, Hamedi M. Numerical and experimental investigation of process parameters in non-isothermal forward extrusion of Ti-6Al-4V [J]. International Journal of Advanced Manufacturing Technology, 2014, 75: 33-44.
[11] Simpson T W, Lin Dennis K J, Chen W. Sampling strategies for computer experiments: Design and analysis [J]. International Journal of Reliability and Application, 2001, 2: 209-240.
[12] Vairamani G, Senthil Kumar T, Malarvizhi S, Balasubramanian V. Application of response surface methodology to maximize tensile strength and minimize interface hardness of friction welded dissimilar joints of austenitic stainless steel and copper alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 2250-2259.
[13] Bahloul R, Mkaddem A, Dal Santo P, Potiron A. Sheet metal bending optimisation using response surface method, numerical simulation and design of experiments [J]. International Journal of Mechanical Sciences, 2006, 48: 991-1003.
[14] Dang Li, Yang He, Guo Liang-gang, Zheng Wen-da, Zhang Jun. Study on exit temperature evolution during extrusion for large-scale thick-walled Inconel 625 pipe by FE simulation [J]. International Journal of Advanced Manufacturing Technology, 2015, 76: 1421-1435.
[15] Yan Shi-cai. High-temperature high-speed hot deformation behavior of Inconel625 alloy and optimization of high-speed extrusion process for tube of this alloy [D]. Dalian: Dalian University of Technology, 2010. (in Chinese)
[16] Li De-fu, Wu Zhi-gang, Guo Sheng-li, Guo Qing-miao, Peng Hai-jian, Hu Jie. Study on the processing map of GH625 Ni-based alloy deformed at high temperature [J]. Rare Metal Materials and Engineering, 2012, 41: 1026-1031.
[17] Committee of China Aeronautical Materials Handbook. China aeronautical materials handbook [M]. 2nd ed. Beijing: Standards Press of China, 2001. (in Chinese)
[18] Dang Li, Yang He, Guo Liang-gang, Shi Lei, Zheng Wen-da, Zhang Jun. Extrusion limit map of large-scale thick-walled Inconel 625 alloy pipe using FE method [J]. Rare Metal Materials and Engineering, 2014, 43: 2130-2135.
[19] Guo Qing-miao, Li Hai-tao, Li De-fu, Guo Sheng-li, Peng Hai-jian, Hu Jie. Hot extrusion moulding process and microstructure evolution of GH625 superalloy tubes [J]. Chinese Journal of Rare Metals, 2011, 35: 684-689.
[20] Shyy W, Papil N, Vaidyanathan R, Tucker K. Global design optimization for aerodynamics and rocket propulsion components [J]. Progress in Aerospace Sciences, 2011, 37: 59-118.
[21] Kapoor R, Nemat-Nasser S. Determination of temperature rise during high strain rate deformation [J]. Mechanics of Materials, 1998, 27: 1-12.
郭良刚1,党 利1,杨 合1,张 君2,郑文达2
1. 西北工业大学 凝固技术国家重点实验室,材料学院,西安 710072;
2. 西安重型机械研究院有限责任公司,西安 710032
摘 要:研究确定难变形Inconel 625合金大型厚壁管挤压加工窗口,是获得具有良好组织性能挤压管材的关键。采用响应面法建立了一种确定基于温控挤压加工窗口的方法。首先,采用基于有限元计算数据的正交回归方法,建立了分别描述温升和峰值温度与关键挤压参数之间的响应面模型;其次,基于建立的响应面模型,分析揭示了关键挤压参数对温升和温度峰值的交互作用规律;最后,通过绘制挤压速度和初始温度空间峰值温度的等高线图,建立了不同挤压比下挤压加工窗口。基于该挤压加工窗口,可方便快速地确定合适的关键挤压参数组合。
关键词:型材挤压;加工窗口;响应面法;难变形材料;有限元模拟
(Edited by Yun-bin HE)
Foundation item: Project (2009ZX04005-031-11) supported by the Major National Science and Technology Special Project of China; Project (318968) supported by the Marie Curie International Research Staff Exchange Scheme (IRSES, MatProFuture) within the 7th EC Framework Program (FP7); Project (B08040) supported by the 111 Plan, China
Corresponding author: Liang-gang Guo; Tel/Fax: +86-29-8849-5632; E-mail: glgglg66@nwpu.edu.cn
DOI: 10.1016/S1003-6326(16)64304-2

