文章编号：1004-0609(2012)08-2347-06

中心圆孔圆盘试件三维最大无量纲应力强度因子的标定

张  盛¹，梁亚磊^{1, 2}

(1. 河南理工大学 能源科学与工程学院，焦作 454003；

2. 中国平煤神马集团十矿，平顶山 467000)

摘  要：基于平面假设标定的圆盘试件的无量纲应力强度因子对岩石断裂韧度的准确测定有一定的影响。使用三维断裂分析软件FRANC3D对不同中心孔尺寸的中心圆孔平台巴西圆盘HFBD试件的三维最大无量纲应力强度因子进行准确标定。结果表明：沿着圆盘厚度方向虚拟三维裂纹前缘各点的最大无量纲应力强度因子并不相等，其中心点与二维标定值最大误差接近3%，推荐了一种不受三维尺寸影响可简化为二维分析的中心圆孔平台圆盘试件尺寸。

关键词：中心圆孔圆盘试件；三维应力强度因子；岩石断裂韧度

中图分类号：TD313          　　     文献标志码：A

Calibration of three-dimensional maximum dimensionless stress intensity factor of holed flattened Brazilion disc specimen

ZHANG Sheng¹, LIANG Ya-lei^{1, 2}

(1. School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China;

2. China Pingmei Shenma Group No.10 Coal Mine, Pingdingshan 467000, China)

Abstract: There was a certain effect to measure accurately the rock fracture toughness with holed disc specimens, of which the maximum dimensionless of stress intensity factor was calibrated with 2D method. By three-dimensional fracture analysis software FRANC3D, the maximum dimensionless of the stress intensity factor of disc samples was calculated, which has different radius sizes of center hole. The results show that the factors on the crack the front edge along the disc thickness direction are varied, even the maximum relative error of the center point is about 3%, compared to the value made with 2D method. A type of holed flattened Brazilian disc specimen is recommend, which can be simplified to a two-dimensional problem without three-dimensional size effect.

Key words: holed flattened Brazilian disc specimen; three-dimensional stress intensity factor; rock fracture toughness

在矿井巷道支护、水压致裂法测定地应力以及爆破施工等工程中都涉及到岩石断裂问题，岩石断裂韧度在这些领域已经得到一定的应用，但其准确测定仍然存在很多问题。如裂缝难以预制、无量纲应力强度因子标定不准确、不同测试方法测定的岩石断裂韧度存在较大的差异等^[1]。针对这些问题，1995年国际岩石力学协会推荐了一种人字形切槽巴西圆盘试件(Cracked chevron notched Brazilian disc, CCNBD)测试岩石Ⅰ型断裂韧度的方法^[2]；由于该类圆盘试样具有体积小，加载方便，对试验设备要求不高等优点，得到了研究者的推广。但是CCNBD试件构形复杂，不能按平面问题进行分析，其断裂韧度公式中的无量纲应力强度因子的准确标定就是一个非常复杂的工作，贾学明和王启智^[3]、樊鸿等^[4]先后对其进行了大量的标定和修正工作。基于圆盘试件的优点，同时为了避免CCNBD复杂的三维构形，王启智和贾学明^[5]提出采用平台巴西圆盘(Flattened Brazilian disc, FBD)进行岩石断裂韧度的测试；随后，张盛和王启智^[6]进一步比较了5种不同类型圆盘的测试方法。相对于需要提前预制裂缝的圆盘试件，中心圆孔平台圆盘试件(Holed flattened Brazilian disc, HFBD)试件更容易制作，而且比FBD试件更能引发中心裂纹产生并避免加载端效应^[6-7]。但是，由于HFBD试件具有三维构形，采用平面分析的方法对HFBD试件进行无量纲应力强度因子的标定，可能会由于不同的中心孔径尺寸造成标定值的较大误差，从而影响岩石断裂韧度值的准确测定。

长期以来，一些研究者使用不同的方法来获得裂纹体裂纹前缘的应力强度因子。张玉军和李治国^[8]采用有限元位移法分析了带裂纹隧道二次衬砌裂纹尖端的应力强度因子。王承强和郑长良^[9]利用平面扇形域哈密顿体系方程，通过分离变量法及共轭辛本征函数向量展开法，推导出一个圆形奇异解析单元列阵用于求解平面裂纹的应力强度因子。黄海燕和刘小健^[10]分别使用节点位移解析法和有限元法计算了含中心裂纹有限加筋板的应力强度因子，并通过对比和分析，提出了一个用于评估应力强度因子计算精度的参数。但是，这些研究都基于平面假设，其计算结果并没有考虑三维裂纹的影响。事实上，受载裂纹体裂纹前缘应力强度因子沿其前缘分布并不一致，樊鸿和张盛^[11]采用应力初始单元法进行三维裂纹的分析，但该方法构造裂纹非常复杂，计算工作量较大。鉴于此，使用专业的三维断裂分析软件FRANC3D(Fracture analysis code in three dimensions)计算HFBD试件受载起裂时的三维裂纹的应力强度因子^[12]，并研究圆盘试件中心孔径尺寸对最大无量纲应力强度因子的影响，对断裂韧度公式中的最大无量纲应力强度因子系数进行了修正。本文作者对三维裂纹进行无量纲应力强度因子的标定将有助于建立更加合理的断裂韧度公式，为准确获得岩石的动态断裂韧度值奠定基础。

1  HFBD试件测试岩石断裂韧度的 原理

在试件中预制裂缝的宽度和形状会给岩石断裂韧度的测试值带来很大的误差^[13]，而对于HFBD和FBD试件都不需要预先制作裂缝。它们的测试原理是从普通巴西圆盘试件测试岩石断裂韧度的方法推广而来   的^[14-15]。试件受力以后，会产生裂纹，通过临界裂纹对应的最大无量纲应力强度因子和二次倒拐的局部最小载荷来确定断裂韧度值^[6]。

如图1(a)所示，HFBD试件受均布压力载荷作用后，沿加载直径AB方向中心孔边引起高度的应力集中。随着加载载荷的增大，裂纹首先在孔边应力集中处萌生，进而沿加载直径AB方向扩展^[6-7]，HFBD试件利用孔边高度的应力集中来帮助试件在中心圆孔边发生起裂，产生裂纹，形成中心圆孔裂纹平台圆盘试件(Hole-cracked flattened Brazilian disc, HCFBD)，如图1(b)所示。根据裂纹扩展过程中临界裂纹长度与之对应的局部最小载荷与最大无量纲应力强度因子的一致关系确定断裂韧度值。

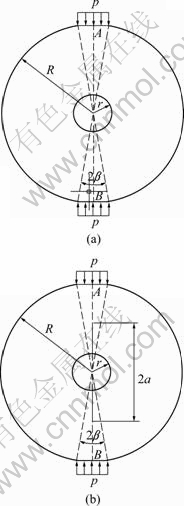
图1  圆盘试件加载及尺寸参数示意图

Fig. 1  Loading and dimension diagram of disc sample: (a) Holed flatterned Brazilian disc; (b) Holed-cracked flattened Brazilian disc

如图1所示，HFBD试件受均布压力合力为p，加载角为2β，半径为R，裂纹扩展长度为2a，厚度为t，中心孔半径为r。根据文献[6]，由该类圆盘试件确定的应力强度因子如式(1)所示，断裂韧度值表达式如式(2)所示：

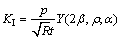                         (1)

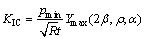                     (2)

式中：K_I为试样受载起裂后裂纹前缘应力强度因子；K_IC为试验测试的岩石的断裂韧度值；Y为无量纲应力强度因子；ρ=r/R为圆盘试件中心孔半径与圆盘半径之比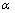；为无量纲裂纹长度，是裂纹扩展长度与圆盘半径之比a/R；p_min为加载曲线上的局部最小载荷； Y_max为临界裂纹长度与之对应的最大无量纲应力强度因子。

当裂纹前缘应力强度因子达到某个临界值时，裂纹发生扩展，此时这个应力强度因子临界值称为断裂韧度。根据断裂原理，在受载材料裂纹扩展过程中的任何载荷p以及其对应的裂纹长度可由式(1)计算得出岩石断裂韧度。但是，脆性材料的裂纹扩展速度非常快，很难精确确定在某一载荷时的裂纹长度。所以，无法使用式(1)直接计算岩石材料的断裂韧度。然而，中心圆孔平台巴西圆盘试件在加载时载荷随裂纹长度的变化情况对应于无量纲应力强度因子的变化情况，即随着裂纹的扩展无量纲应力强度因子经历了上升、最大值、下降的过程，其最大无量纲应力强度因子Y_max正好对应于加载曲线上局部最小载荷p_min(此时，临界裂纹长度与之对应)^[6]。因此，可由p_min和Y_max代入式(2)计算岩石断裂韧度K_IC。

2  三维裂纹模拟分析

通过上面的分析可知，HFBD试件在标定其最大无量纲应力强度因子时，需要在HFBD的基础上构造虚拟裂纹从而形成HCFBD试件，根据虚拟裂纹计算其受载后裂纹扩展过程中沿厚度方向不同点处的应力强度因子，从而确定其最大无量纲应力强度因子。采用三维断裂分析软件FRANC3D可进行三维虚拟裂纹的模拟分析。FRANC3D^[12]是美国康奈尔大学断裂工作组(Cornell fracture group, CFG)自主研发的一套具有建模、应力分析、应力强度因子计算、裂纹自动扩展模拟等功能的软件。模拟裂纹能力是FRANC3D的特色之一，用户可以通过内置裂纹库或者以文件的方式生成所需要的裂纹。对于裂纹的构形，可以设置任意的裂纹前缘。对模型计算结束后，用户可以储存应力强度因子计算结果，以便调用。

基于本文作者的前期工作，采用HFBD圆盘试件能够测试岩石的断裂韧度^[6]，但该方法是建立在二维平面分析的基础上的，在此拟进行三维分析。根据圆盘试件的对称性，取其一半进行建模，如图2所示。模型几何参数为：R=40mm，ρ=0.2，2β=20°，t=30 mm。大理岩材料参数：弹性模量E=1.63 GPa，泊松比μ=0.3。

考虑到裂纹沿模型厚度Z方向的对称性，主要取沿模型标准化一半厚度方向3个点处的应力强度因子，即取无量纲厚度λ=2Z/t为0、0.25、0.5处的应力强度因子，λ=0代表圆盘沿厚度方向外部表面处应力强度因子，λ=0.25代表圆盘沿厚度方向1/4处点的应力强度因子，λ=0.5代表圆盘沿厚度方向中心处点应力强度因子。

根据FRANC3D的计算，得到中心孔径ρ=0.2，在不同的裂纹长度条件下，无量纲裂纹应力强度因子Y_max与无量纲裂纹长度a/R的关系如图3所示，其中，横坐标代表无量纲裂纹长度即裂纹长度a和圆盘半径R之比，纵坐标代表无量纲应力强度因子Y。

图2  圆盘试件三维模型(一半)

Fig. 2  Three dimensions model of disc specimen (half)

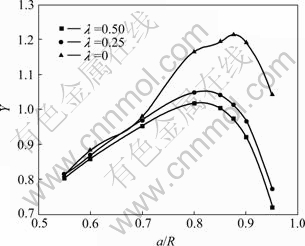
图3  无量纲应力强度因子Y和无量纲裂纹长度a/R的关系

Fig. 3  Relation between dimensionless stress intensity factor Y and dimensionless crack length a/R

从图3可以看出，圆盘试件裂纹前缘中心点，1/4点以及表面点的无量纲应力强度因子随着裂纹长度的增加，无量纲应力强度因子随着裂纹长度的增加先增加后减小；沿厚度方向的分布有较大差异；而最大无量纲应力强度因子所对应的裂纹长度并不一致，其值相差也较大。当λ=0时，Y_max=1.214；当λ=0.25时，Y_max=1.048；当λ=0.5 时，Y_max=1.017；裂纹前缘圆盘表面点处的最大无量纲应力强度因子Y_max比中心点处的Y_max大了16.2%。另外，使用有限元软件ANSYS对该类圆盘试件进行平面问题处理，得到二维计算的Y_max结果为1.038，这比三维方法计算的中心点处Y_max大2.1%。其原因可能是由于三维裂纹考虑了靠近圆盘两个端面到中心整个裂纹长度的情况，由于靠近两端面的自由表面上沿裂纹切线方向的位移不受限制，有明显的泊松比效应，背离了平面应变情况，所以与平面问题处理产生一定的误差。

3  HFBD试件断裂韧度公式的三维 修正

对圆盘半径R=40 mm、加载角2β=20°、厚度t=30 mm，9种不同孔径比(ρ)HFBD试件(ρ为0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5)，进行的大量三维应力强度因子和二维应力强度因子计算后，得到最大无量纲应力强度因子Y_max和孔径比ρ的关系如图4所示。

从图4可以看出，随着圆盘试件中心孔径ρ的增大，裂纹前缘表面点、中心点和采用二维应力强度因子计算方法确定的最大无量纲应力强度因子Y_max都在增大；由二维计算方法确定的Y_max，与三维计算方法圆盘中心确定的Y_max最大误差为3.0%；与三维计算  方法圆盘表面裂纹前缘点确定的Y_max最大误差为27.8%。

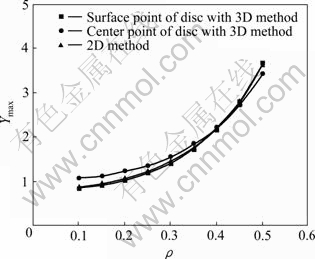
图4  最大无量纲应力强度因子Y_max和孔径比ρ的关系

Fig. 4  Relationship between biggest dimensional stress intensity factor Y_max and dimensional hole size ρ

如果采用圆盘中心处点的Y_max代入式(2)计算材料的断裂韧度，经过曲线拟合如图5所示，得到三维方法计算的圆盘中心点标定的Y_max与中心孔径比ρ的函数表达式如式(3)所示：

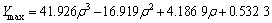  (3)

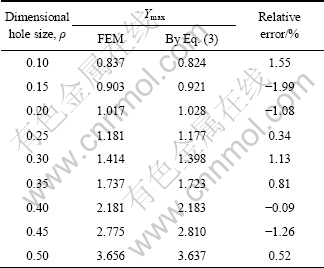
经验证，在HFBD试件中心孔径ρ为0.1~0.5范围内，由式(3)得出的最大无量纲应力强度因子Y_max与有限元计算标定的值最大误差小于2.0%，如表1所列。

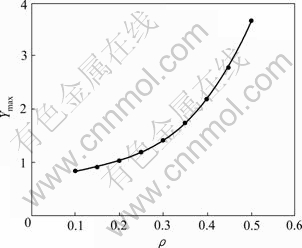
图5  圆盘中心点最大无量纲应力强度因子Y_max与中心孔径比ρ的关系拟合曲线

Fig. 5  Fitting curve for biggest dimensional stress intensity factor Y_max of center point with diemnsional hole size ρ

表1  有限元与式(3)中Y_max计算值的比较

Table 1  Comparison of Y_max calculation results by FEM and formula (3)

通过比较圆盘试件裂纹前缘表面点和中心处点的Y_max发现：在中心孔径比ρ为0.1~0.4范围内，裂纹前缘表面点与裂纹前缘中心点、二维方法确定的Y_max的差值随ρ的增大而由大变小；在ρ=0.4附近，裂纹前缘表面点、中心点处Y_max与二维方法确定的Y_max基本上相等，二维Y_max比裂纹前缘中心点Y_max大0.41%、比裂纹前缘表面点Y_max小0.46%；在ρ为0.4~0.5范围内，裂纹前缘表面点、中心处点Y_max的差值随ρ的增大而由小变大。

从上面的分析可以得出，采用中心孔径ρ=0.4的HFBD试件，最大无量纲应力强度因子Y_max受三维尺寸的影响可以忽略。因此，作者推荐一种用来测试岩石断裂韧度的较为理想的中心圆孔圆盘试件，即圆盘的半径R=40 mm，圆盘厚度t=30 mm，平台加载角2β=20°，中心孔径比ρ=0.4，此时由三维方法计算的圆盘表面点、圆盘中心点及二维方法计算的Y_max分别为2.20、2.18、2.19，所采用断裂韧度的计算公式如下。

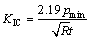                             (4)

由该尺寸和公式得到的断裂韧度值基本不受三维尺寸的影响，能够采用平面分析得到准确的测试值。

4  结论

1) HFBD试件虚拟裂纹前缘不同点的最大无量纲应力强度因子值各不相同，随着圆盘试件中心孔径比ρ的增大，各点的最大无量纲应力强度因子Y_max都在增大，由二维计算方法标定的值相比于三维方法计算的圆盘中心点确定的Y_max最大误差接近3%，因此，不能简单地采用平面问题进行HFBD试件最大无量纲应力强度因子的标定。

2) 推荐了一种能够基于平面问题进行分析测试岩石断裂韧度的HFBD试件，该圆盘直径R=40 mm，厚度R=30 mm，平台加载角 2β=20°，中心孔径比ρ=0.4，其断裂韧度的计算公式如式(4)所示。

REFERENCES

[1] 崔振东, 刘大安, 安光明, 周 苗. 岩石Ⅰ型断裂韧度测试方法研究进展[J]. 测试技术学报, 2009, 3(2): 189-196.
CUI Zhen-dong, LIU Da-an, AN Guang-ming, ZHOU Miao. Research progress in mode-Ⅰfracture toughness testing methods for rocks[J]. Journal of Test and Measurement Technology, 2009, 3(2): 189-196.

[2] ISRM Testing Commission. Suggested method for determining mode (Ⅰ): Fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32: 57-64.

[3] 贾学明, 王启智. 断裂韧度试样CCNBD宽范围应力强度因子标定[J]. 岩土力学, 2003, 21(6): 907-912.
JIA Xue-ming, WANG Qi-zhi. Wide range calibration of the stress intensity factor for the fracture toughness specimen CCNBD[J]. Rock and Soil Mechanics, 2004, 21(6): 764-768.

[4] 樊 鸿, 张 盛, 王启智. 岩石断裂韧度试样CCNBD临界应力强度因子的全新数值标定[C]//中国计算力学大会’2010(CCCM2010)暨第八届南方计算力学学术会议(SCCM8)论文集. 绵阳: 西南科技大学, 2010-08-20.
FAN Hong, ZHANG Sheng, WANG Qi-zhi. A completely new numerical calibration of the critical stress intensity factor for the rock fracture toughness specimen CCNBD[C]//The 2010th China Conference on Computational Mechanics and the 8th South Conference on Computational Mechanics. Mianyang: Southwest University of Science and Technology, 2010-08-20.

[5] 王启智, 贾学明. 用平台巴西圆盘试样确定脆性岩石的弹性模量、拉伸强度和断裂韧度—第一部分: 解析和数值结果[J]. 岩石力学与工程学报, 2002, 21(9): 1285-1289.
WANG Qi-zhi, JIA Xue-ming. Determination of elastic modulus, tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen—Part Ⅰ: Analytical and numerical results[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(9): 1285-1289.

[6] 张 盛, 王启智. 用五种圆盘试件的劈裂试验确定岩石断裂韧度[J]. 岩土力学, 2009, 30(1): 12-18.
ZHANG Sheng, WANG Qi-zhi. Determination of rock fracture toughness by split test using five types of disc specimen[J]. Rock and Soil Mechanics, 2009, 30(1): 12-18.

[7] FISCHER M P, ELSWORTH D, ALLEY R B, ENGELDER T. Finite element analysis of the modified ring rest for determining mode (Ⅰ): Fracture toughness[J]. International Journal of Rock Mechanics & Mining Sciences, 1996, 33(1): 1-15.

[8] 张玉军, 李治国. 带裂纹隧道二次衬砌承载能力的平面有限元计算分析[J]. 岩土力学, 2005, 26(8): 1201-1206.
ZHANG Yu-jun, LI Zhi-guo. 2D finite element analysis of bearing capacity of tunnel lining with cracks[J]. Rock and Soil Mechanics, 2005, 26(8): 1201-1206.

[9] 王承强, 郑长良. 平面裂纹应力强度因子的半解析半有限元法[J]. 工程力学, 2005, 22(1): 33-37.
WANG Chen-qiang, ZHENG Chang-liang. Semi-analytical finite element method for plane crack stress intensity factor[J]. Engineering Mechanics, 2005, 22(1): 33-37.

[10] 黄海燕, 刘小健. 含中心裂纹有限加筋板应力强度因子的计算精度评估[J]. 船舶力学, 2008, 12(5): 765-769.
HUANG Hai-yan, LIU Xiao-jian. Accuracy evaluation of stress intensity factor about stiffened plate with a central crack[J]. Journal of Ship Mechanics, 2008, 12(5): 765-769.

[11] 樊 鸿, 张 盛. 求解应力强度因子的单元初始应力法[J]. 武汉理工大学学报, 2008, 30(11): 90-93.
FAN Hong, ZHANG Sheng. An unit initial stress method to calculate stress intensity factor[J]. Journal of Wuhan University of Technology, 2008, 30(11): 90-93.

[12] 贾学明, 王启智. 三维断裂分析软件FRANC3D[J]. 计算力学学报, 2004, 21(6): 764-768.
JIA Xue-ming, WANG Qi-zhi. Three-dimensional fracture analysis software[J]. Chinese Journal of Computational Mechanics, 2004, 21(6): 764-768.

[13] CHEN M, ZHANG G Q. Laboratory measurement and interpretation of the fracture toughness of formation rocks at great depth[J]. Journal of Petroleum Science and Engineering, 2004, 41: 221-231.

[14] GUO H, AZIZ N I, SCHMIDT L C. Rock fracture toughness determination by the Brazilian test[J]. Engineer Geology, 1993, 33(2): 177-188.

[15] YANG S C, TANG T X, ZOLLINGER D, GURJAR A. Splitting tension tests to determine concrete fracture parameters by peak-load method[J]. Advn Cem Bas Mat, 1997, 5: 18-28.

(编辑 龙怀中)

基金项目：国家自然科学基金青年基金资助项目(51004043)；河南理工大学博士基金资助项目(B2008-66648270)；河南省教育厅自然科学基础研究计划项目(021- 2010A440005)

收稿日期：2011-07-21；修订日期：2011-12-10

通信作者：张  盛，副教授；电话：18603918628；E-mail: zhangs@hpu.edu.cn