Hopfield神经网盲检测统计信息缺失信号
阮秀凯1,张志涌2
(1. 南京邮电大学 通信与信息工程学院,江苏 南京,210003;
2. 南京邮电大学 自动化学院,江苏 南京,210046)
摘要:考虑到现代无线通信系统信号的高频化特性,采用连续输入的神经元是接近物理现实,并利用连续Hopfield型神经网络本身特点,提出如何运用复连续Hopfield网络解决统计信息缺失信号的盲检测问题。研究统计信息缺失的信号盲检测的优化问题构造和能量函数的映射,给出该特定问题的能量函数、正确盲检测信号权矩阵的配置方法。最后通过仿真验证算法的有效性和鲁棒性并指出未来的研究方向。
关键词:盲检测;连续复Hopfield神经网络;统计信息缺失;能量函数;激活函数
中图分类号:TN911.7 文献标志码:A 文章编号:1672-7207(2011)S1-0012-05
Hopfield neural network detect blindly signals with missing statistics information
RUAN Xiu-kai1, ZHANG Zhi-yong 2
(1. College of Telecommunications and Information, Nanjing University of Posts and Telecommunications,
Nanjing 210003, China;
2. College of Automation, Nanjing University of Posts and Telecommunications, Nanjing 210003, China)
Abstract: Based on the fact that both the continuous Hopfield neural network (CHNN) characteristics and the high frequency characteristics of signals in modern wireless communication systems that continuous input neurons are close to true physical fact are taken into account, a new blind detection algorithm of the signals with missing statistics information using complex CHNN was proposed. The method of mapping the cost function of this optimization problem to the energy function of CHNN is proposed. How to map the cost function of this optimization problem to the energy function of CHNN was studied. Meantime, a special connective matrix was constructed to ensure the detect signals correctly was illustrated to ensure the detect signals correctly. Simulation results demonstrate the effectiveness and robustness of this new algorithm.
Key words: blind detection; continuous complex Hopfield neural network; missing statistics information; energy function; activation function
盲均衡/盲检测技术经过了20多年的发展,算法层出不穷[1]。但时至今日,已有的性能较优秀的传统盲检测算法大多构建在统计量基础上,使得算法严重依赖数据量长度,即为保证统计量的精确性,必定需要足够长的数据量。当运用于短数据场合时,数据的统计信息将会失真或完全偏离真实统计值,使得算法性能降低或完全失效。特别地,随着传感网(Internet of things)和泛在网(Ubiquitous network)的兴起,传感器能耗问题尤为突出,且此时大规模网络节点往往无法获得足够长的数据量,这使得盲检测算法的设计和实际应用必须要求数据长度短,适用于信息统计失真/缺失的场合且算法收敛速度增快。文献[2]提出了直接利用字符集检测信号的算法,但它们仅对最简单二值实数信号有效,而对于稍复杂的四进制相移键控(Quaternary phase shift keying, QPSK),就会使计算量增大而效率大减。当信号统计信息失真/缺失时,传统基于统计量的盲检测/均衡算法多数失效。运用神经网络实现盲信号处理[3-6]的文献并不少见,该类方法虽然减少了算法对数据量的过多依赖,但是,算法运算负担相当重。考虑到现代无线通信系统信号的高频化特性,本文作者基于连续输入的神经元接近物理现实,并利用连续Hopfield型神经网络(Continuous Hopfield neural network, CHNN)本身特点,提出如何运用复连续Hopfield神经网络解决QPSK信号的盲检测问题。完成统计信息缺失的信号盲检测的优化问题构造和能量函数的映射,给出该特定问题的能量函数、正确盲检测信号权矩阵的配置方法。最后通过仿真分析,进一步讨论算法的有效性和鲁棒性并指出未来的研究方向。
1 CHNN概述
Hopfield网络是单层对称全反馈网络(也可无自反馈),根据激活函数和输入输出量的不同,可分为离散型Hopfield网络(Discrete Hopfield neural network, DHNN)和连续型的Hopfield网络,其中,离散型模型可视为连续型模型的特殊形式。CHNN是Hopfield基于模拟生物神经网络的并行性、分布式存储特性、联想性及大规模协同处理的能力,于1984年提出的[7]。CHNN在时间上是连续的,所以,网络中各神经元处于同步工作模式,基于Hopfield模型的优化计算具有简单、规范和快速等优点。在实际应用中,任何一个系统,如果其优化问题可以用能量函数作为目标函数,那么,总可以用CHNN对其进行求解。由于引入能量函数,Hopfield使神经网络和问题优化直接对应。
利用神经网络进行优化计算,就是给神经网络这一动力系统给出初始的估计点即初始条件;然后,随网络的运动传递而找到相应极小点。这样,优化问题就可以用CHNN进行求解,这也是Hopfield网络用于神经计算的基本原因。另一方面,选择CHNN解决信号盲检测问题的出发点还因为考虑到现代无线通信系统的信号的高频化特性,输入信号向量需要“密集”量化,采用连续输入的神经元更接近物理现实。
2 基于复CHNN的信号盲检测
2.1 构造优化问题
单输入多输出SIMO(Single-input multi-output)连续时间信号的接收方程、盲处理方程为: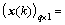
 ,
,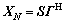 。其中:发送信号阵
。其中:发送信号阵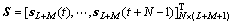 ;
;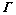 是由hj (j=0, 1, …, M)构成的维数为
是由hj (j=0, 1, …, M)构成的维数为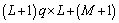 的块Toeplitz矩阵;
的块Toeplitz矩阵;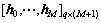 是通信信道的冲激响应,接收数据阵
是通信信道的冲激响应,接收数据阵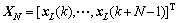 。将接收数据阵矩阵进行奇异值分解,有
。将接收数据阵矩阵进行奇异值分解,有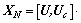
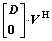 ,当
,当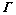 满列秩时,则有
满列秩时,则有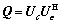 ,满足
,满足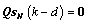 。其中:d=0, …, M+L,且
。其中:d=0, …, M+L,且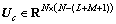 。
。
据此构造性能函数及优化问题[2]:
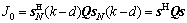 (1)
(1)
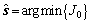 (2)
(2)
其中: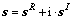 ,表示复向量,其元素的实部、虚部都属于集合A,
,表示复向量,其元素的实部、虚部都属于集合A,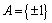 。可以发现在整个优化问题的构造过程中,并未使用到发送源信号的任何统计信息。
。可以发现在整个优化问题的构造过程中,并未使用到发送源信号的任何统计信息。
2.2 CHNN模型和动态方程
考虑具有N个互连接的Hopfield网络[8]。忽略神经元内部传播时间延迟,定义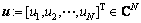 ,神经元输出向量
,神经元输出向量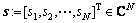 ,激活函数矩阵
,激活函数矩阵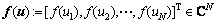 。RC电路矩阵
。RC电路矩阵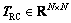 ,连接权矩阵
,连接权矩阵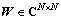 ,且有
,且有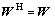 。连续时间连续状态Hopfield神经网结构见图1,采用文献[8]的Hopfield网络模型,针对通信系统的盲检测问题,设置电流偏置为0。
。连续时间连续状态Hopfield神经网结构见图1,采用文献[8]的Hopfield网络模型,针对通信系统的盲检测问题,设置电流偏置为0。
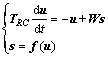 (3)
(3)
进而写出网络的动态方程为
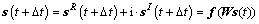 (4)
(4)
其中: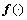 为由激活函数所构成的非线性算子。
为由激活函数所构成的非线性算子。
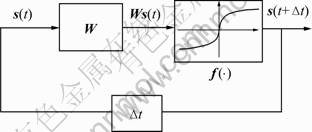
图1 CHNN结构示意图
Fig.1 CHNN diagram
2.3 复激活函数和能量函数
通用的复激活函数形式[8]表示如下:
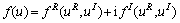
这里: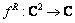 ;
;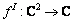 ;uR和uI分别表示变量u的实部和虚部[8]。
;uR和uI分别表示变量u的实部和虚部[8]。
假设所有神经元均具有相同形式的复激活函数,且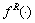 和
和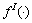 具有相同的解析函数形式。复Sigmoid函数
具有相同的解析函数形式。复Sigmoid函数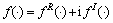 ,且
,且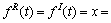
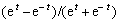 。其中:
。其中: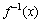 是f(t)的反函数,具体形式为
是f(t)的反函数,具体形式为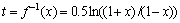 ,其中
,其中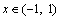 。显然,f(t)和
。显然,f(t)和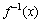 均具有连续可微、有界且严格单调递增特性。
均具有连续可微、有界且严格单调递增特性。
采用文献[8]的能量函数:
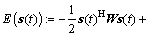
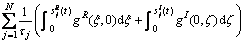
其中: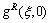 和
和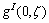 分别表示复激活函数实部和虚部的逆函数。
分别表示复激活函数实部和虚部的逆函数。
对于盲检测所构造的优化问题而言,希望网络具有唯一平衡点,并且要求它是全局渐近稳定的。该能量函数是否适用该优化问题并满足网络平衡点是全局渐近稳定点的证明见文献[8]。随着时间的演化,网络神经元的输出即网络方程解的轨迹在状态空间中总是朝着使能量函数值减小的方向运动,稳定平衡点就是能量函数的极小点。
2.4 互连权阵配置
确定了能量函数形式之后,随之而来的问题是如何设置网络结构参数使得与该盲检测问题的能量函数相对应。
为运用复CHNN求解的信号盲检测问题,Hopfield网络的连接权矩阵可作如下配置: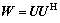 。显然,W为幂等矩阵,其特征值非零即1,由此方式所构造的权矩阵必为一非负定矩阵。对于同种结构的网络,当连接权值发生变化时(即网络本身发生了变化),网络能量函数极小点的个数和值也会随之改变,将直接导致能量函数的波动而无法递减。
。显然,W为幂等矩阵,其特征值非零即1,由此方式所构造的权矩阵必为一非负定矩阵。对于同种结构的网络,当连接权值发生变化时(即网络本身发生了变化),网络能量函数极小点的个数和值也会随之改变,将直接导致能量函数的波动而无法递减。
下面讨论据此配置权矩阵对网络平衡点产生的作用。设待检测的信号序列为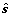 ,
,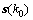 为网络的任一平衡点。
为网络的任一平衡点。
因为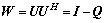 ,根据动态更新方程,有
,根据动态更新方程,有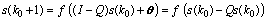 。因为
。因为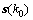 为网络的某一平衡点,故必有
为网络的某一平衡点,故必有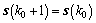 ,要使上式成立,则必须要满足
,要使上式成立,则必须要满足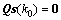 。因为
。因为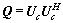 ,故有
,故有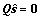 ;又因为
;又因为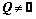 ,所以,当且仅当
,所以,当且仅当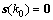 或
或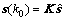 时成立(K为非零矩阵)。所以,权矩阵如上配置的Hopfield网络的平衡点必是原点或待检测信号
时成立(K为非零矩阵)。所以,权矩阵如上配置的Hopfield网络的平衡点必是原点或待检测信号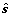 的线性组合。
的线性组合。
而随机初始信号经激活函数首次映射后,所有状态数据会向坐标原点收缩,这样就需要一个大于1的正增益因子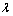 使得搜索空间扩大,使得激活函数进一步达到理想映射,即
使得搜索空间扩大,使得激活函数进一步达到理想映射,即 。值得指出的是:因子
。值得指出的是:因子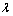 的加入虽不会改变网络结构本身,但是
的加入虽不会改变网络结构本身,但是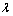 并非随意设置。若
并非随意设置。若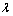 过小,则无法达到使搜索空间有效扩大的目的,而若
过小,则无法达到使搜索空间有效扩大的目的,而若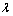 过大,则使得数据点向信号星座点字符集的最大字符处汇聚。随着反馈的不断进行,该作用将不断叠加,从而导致算法失效。
过大,则使得数据点向信号星座点字符集的最大字符处汇聚。随着反馈的不断进行,该作用将不断叠加,从而导致算法失效。
2.5 网络运行终止条件设置
Hopfield 神经网络比较常用的终止条件有:迭代过程中能量函数值与理想能量之间的差值小于某个阈值或者预先设定反馈终止次数。但是,对于同一问题,神经元数目的选择直接决定问题规模的不同,使网络收敛所需要的反馈次数也不尽相同,设置一个固定的反馈次数使得算法缺乏自适应性。而Hopfield 网络可能含有多个局部极小点,并不能保证每一次迭代都可以达到最终的全局最小点,所以,采用能量函数与正确的能量之间的差值的方式会增大网络的运行时间,甚至无法找到令人满意的解,而且要获得正确能量需要先验获得。基于以上原因,采用迭代过程中能量函数的增量作为网络运行的终止条件。仿真中采用该差值为-10-6。结果证明:该条件可简单有效地满足算法要求。
3 仿真实验与分析
仿真参数作如下约定:
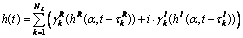
经过采样的多径合成复信道。其中: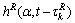 ,
,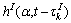 分别是滚降因子
分别是滚降因子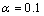 、延迟因子
、延迟因子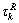 和
和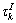 随机产生的升余弦脉冲响应,整个脉冲的长度为6个基带采样周期;
随机产生的升余弦脉冲响应,整个脉冲的长度为6个基带采样周期; 和
和 是在(0, 1)区间均匀分布的随机权系数。均衡器阶数L=8,过采样因子/接收天线个数q=4,信号传播多径数NL=5,τj=20(j=1, 2, …, N),能量函数和比特误码率(Bit error rate,BER)平均曲线均通过Monte Carlo试验获得。采用QPSK信号,信号序列呈非均匀分布,且某个符号点上的符号数特别多,而其中一个符号点上的符号数特别少,信号概率分布见图2。
是在(0, 1)区间均匀分布的随机权系数。均衡器阶数L=8,过采样因子/接收天线个数q=4,信号传播多径数NL=5,τj=20(j=1, 2, …, N),能量函数和比特误码率(Bit error rate,BER)平均曲线均通过Monte Carlo试验获得。采用QPSK信号,信号序列呈非均匀分布,且某个符号点上的符号数特别多,而其中一个符号点上的符号数特别少,信号概率分布见图2。
3.1 算法性能
图3给出了算法在不同信噪比和数据量情况下的平均比特误码率曲线。对于统计信息缺失的QPSK信号的盲检测,即使在信噪比为10 dB情况下也可以获得完全正确的检测性能。但是,当数据量不足够时(如N为50和100时),网络最终即使达到了稳定态,算法也是收敛的,平衡点也随之获得,但是此时的信号盲检测是失败的。而进一步仿真试验中设置无噪声影响时,数据量不足时也无法获得盲检测效果。同时,发现N=200和 N=300的BER曲线十分接近。这说明数据量增加到一定程度时,算法将达到其性能极限,此时,若持续加大数据量,也只是对系统开销的浪费。
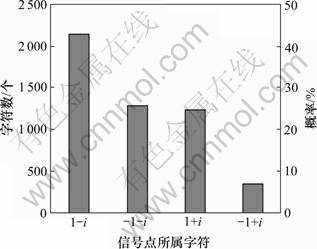
图2 所发送信号点大致概率分布情况
Fig.2 Probability distribution of transmitted signal
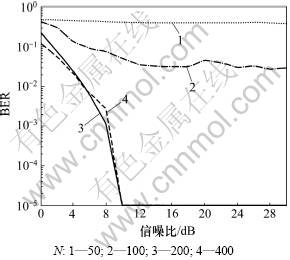
图3 BER曲线
Fig.3 Curve of BER
3.2 新算法与其他盲检测算法的性能对比
通过CHNN算法与经典恒模(Constant modulus algorithm, CMA)算法[1]、支持向量机(Support vector machines, SVM)算法[5]性能对比借以获得性能区别的直观印象。仿真结果均来自单次独立试验列字符:在信噪比为20 dB时,随机发送字符数为106的非均匀分布QPSK序列,CMA算法从中随机抽取N=5 000个字符参与运算,SVM算法从CMA算法随机抽取的字符数中再次抽取N=2 500个字符参与运算,CHNN在SVM算法数据序列中抽取N=200参与运算的情况下获得。3种算法收敛后的输出信号星座分布图形见图4。
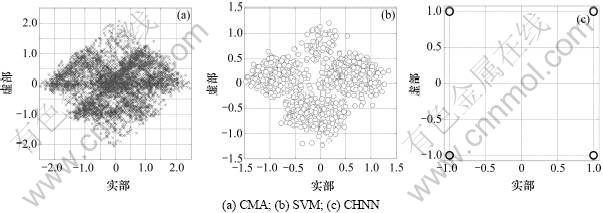
图4 CMA, SVM和CHNN算法输出信号星座图
Fig.4 Output signal constellation of CMA, SVM and CHNN algorithm, respectively
仿真结果表明:在发送序列非均匀分布的情况下,CMA算法完全失效,这是由于信号非均匀分布时,CMA运行过程中所参与运算的统计信息是失真的,而算法默认该些统计特性符号理论值,这直接导致算法失效。而SVM算法虽然在对抗统计信息失真时性能良好,但是,其结果无法满足信号正确盲检测要求。而新算法可以获得理想的盲检测效果,星座点完全匹配于原始发送序列的星座,且不存在信号“祢散”的情况。而且这些仿真结果是在CHNN算法数据量为CMA和SVM算法数据量的1/10~1/25情况下获得的。
4 结论
研究了如何运用复CHNN解决统计信息缺失信号的盲检测问题,完成统计信息缺失的信号盲检测的优化问题构造和能量函数的映射,给出该特定问题的能量函数、正确盲检测信号权矩阵的配置方法。理论分析结果和仿真结果都验证了该算法对统计信息失真、小数据量的信号盲检测问题特别有效。
参考文献:
[1] Romis R A, Joao M R, Charles C C. Unsupervised signal processing: Channel equalization and source separation[M]. New York: CRC Press, 2009: 329-376.
[2] BAI Er-wei, LI Qing-yu, ZHANG Zhi-yong. Blind source separation/channel equalization of nonlinear channels with binary inputs[J]. IEEE Transactions on Signal Processing, 2005, 53(7): 2315-2323.
[3] RUAN Xiu-Kai, ZHANG Zhi-yong. Blind nonlinear channel equalization using kernel processing[C]//Proceedings of the 2009 IEEE International Conference of Image and Signal Processing. Tianjing, China, 2009: 4406-4411.
[4] Han S, Lee I, Pedrycz W. Modified fuzzy c-means and Bayesian equalizer for non-linear blind channel[J]. Applied Soft Computing, 2009, 9(3): 1090-1096.
[5] Marcelino L, Jonathan G O. Blind equalization using the IRWLS formulation of the support vector machine[J]. Signal Processing, 2009, 89(7): 1436-1445.
[6] Burse K, Yadav R N, Shrivastava S C. Channel equalization using neural network: a review[J]. IEEE Transactions on Systems, Man, and Cybernetics: Part C, 2010, 40(3): 352-357.
[7] Hopfield J J. Neurons with graded response have collective computational properties like those of two-state neurons[J]. Proceedings of the National Academy of Sciences of the United States of America, 1984, 81(10): 3088-3092.
[8] Tohru N. Complex-valued neural networks: Utilizing high- dimensional parameters[M]. New York: Hershey, 2009: 123-232.
(编辑 陈灿华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(60772060)
通信作者:阮秀凯(1979-),男,浙江乐清人,博士研究生,从事智能信号与信息处理研究;电话:15251875712;E-mail: ruanxiukai@163.com