DOI: 10.11817/j.issn.1672-7207.2016.07.036

高陡起伏地形GPR偏移的波场延拓及精度分析

石明^{1, 2}，戴前伟^{1, 3}，冯德山^{1, 3}，张彬^{1, 3}，尹小波^{1, 3}

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；

2. 贵州省有色金属和核工业地质勘查局物化探总队，贵州 都匀，558004；

3. 有色金属成矿预测与地质环境监测教育部重点实验室，湖南 长沙，410083)

摘要：基于高陡起伏地形对探地雷达波场的成像精度产生影响，将传统的单微分算子改进为交叉微分算子(CDO);基于交叉微分算子的差分逆时偏移改变传统差分偏移算法的波场延拓方向，给出无近似的波场延拓差分公式、上行波边界条件和实现过程，得到能适应于高陡起伏地形的探地雷达偏移算法，然后以横向速度差异较大的高陡起伏反射模型为例，从波场延拓精度与解析结果、振幅保真加权值、高陡界面能量归位能力、成像剖面4方面分析交叉微分算子偏移法与传统方法的成像精度。研究结果表明：基于交叉微分算子的探地雷达偏移算法能够实现高陡界面的正确归位。

关键词：探地雷达；偏移成像；高陡起伏地形；交叉微分算子；波场延拓

中图分类号：P631          文献标志码：A         文章编号：1672-7207(2016)07-2448-08

Precision analysis of wave-field extrapolation in migration with steep-dip rough terrains for GPR

SHI Ming^{1, 2}, DAI Qianwei^{1, 3}, FENG Deshan^{1, 3}, ZHANG Bin^{1, 3}, YIN Xiaobo^{1, 3}

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;

2. Geophysical and Geochemical Prospecting Team, Nonferrous Metals and Nuclear Industry Geological Exploration Bureau of Guizhou, Duyun 558004, China;

3. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring,

Ministry of Education, Changsha 410083, China)

Abstract: Considering that ground penetrating radar (GPR) is obviously influenced by the inclination angle of reflecting interface, in order to improve the imaging accuracy of steep-dip rough terrains in GPR migration, the single differential operator was replaced by a cross differential operator(CDO), and a reverse-time migration method based on CDO was proposed, which completely changed the direction of wave-field extrapolation, and the implementation of CDO FD migration method was eventually achieved with the precise difference equations and corresponding boundary conditions of up-going GPR wave. Then a laterally variable velocity reflection model with steep-dip rough terrains was presented, particular attention was paid to the precision of wave-field extrapolation in laterally variable velocity, and from wave-field extrapolation precision, fidelity weight of wave amplitude, ability of energy convergence in steep-dip case and migration imaging section to analyze the imaging precision obtained by CDO FD migration method, FD method, F-K method and Kirchhoff method. The results show that the diffraction and scattering can be mostly converged with COD FD migration method, which shows that the COD FD migration method can deal with steep-dip rough terrains of GPR data.

Key words: ground penetrating radar(GPR); migration imaging; steep-dip rough terrains; crossed differential operator (CDO); wave field extrapolation

探地雷达(ground penetrating radar, GPR)数据偏移成像是浅层地球物理勘探精细化反演的重要组成部分，反演结果为偏移成像提供原始的初始速度模型，偏移成像为反演结果提供有效的校正依据^[1-2]。偏移成像的目的是使界面上的反射波归位，绕射点收敛^[3]。探地雷达数据偏移从自激自收剖面的最后1个采样点开始计算，沿着负时间方向进行延拓，根据CLAERBOUT^[4]的爆炸反射界面成像原理，取零时刻的深度剖面为偏移成像剖面。复杂地质构造的波动方程偏移成像方法主要有频率波数域F-K偏移、Kirchhoff积分法偏移、差分偏移和有限元偏移。MUFTI等^[5-7]采用基于单程标量波动方程的差分偏移法，该方法可灵活地处理横向速度剧烈变化的倾斜界面，对小倾角起伏的复杂地层，该算法对原波动方程进行了相应的阶层近似，由于略去了波场沿深度方向上的高阶偏导，这种近似处理对偏移效果影响严重，使得该方法受反射界面的倾角限制，同时解的精度和稳定性也容易受空间采样率、近似的阶乘等级和实现方法的严重影响。GRAY等^[8-11]采用基于射线理论的Kirchhoff积分偏移法，将分散在各道且来自同一个绕射点的能量进行收拢，该方法计算效率高，但需要较精确的速度模型，也不易确定对应的偏移孔径和格林函数，难以处理横向速度剧烈变化的高陡界面，对复杂地质构造的空间归位能力较差。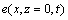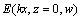STOLT等^[12-15]采用改进的频率波数域相移偏移法经过2次傅里叶变换，将像空间变换为，再对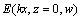进行波场延拓，外推至深度为z处的波场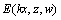，最后再进行2次一维傅里叶逆变换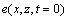。该方法假定波速为恒定值，能够得到精确解，具有精度高、不受地层起伏限制等优点，但该方法均要求地下介质的横向速度不变，难以适应横向速度剧烈变化的高陡起伏地形。由此可见，将各类偏移方法应用于探地雷达领域都有其适用范围和局限性。传统的差分偏移法求解近似波动方程，对雷达波场向下进行延拓成像，能够适应剧烈的横向速度变化，但近似的差分偏移方程受地形起伏的影响严重，对高陡地形反射界面的偏移效果较差，尤其对高陡且横向速度剧烈变化的反射界面，常规时间偏移方法难以使其中的复杂构造正确归位。为此，本文作者从传统差分偏移法中上行波方程产生的误差根源出发，将传统的单微分算子改进为交叉微分算子(crossed differential operator, CDO)，对波动方程进行交叉坐标变换，并采用全新的交叉微分算子差分格式和上行波边界条件，改变雷达波场的延拓方向，以地表雷达波场数据作为初始数据，根据逆时成像原理^[16-18]，从地表记录的波场开始，将某个时间的时间切片逆时传播进入地下，并由波场从切片时间点的反向进行传播，在时间轴上实现外推，恢复零时刻各深度上的雷达波场值，并确保整个波场延拓的偏移过程采用非近似的精确公式。最后以广泛存在于浅地表的高陡起伏地形反射界面为算例，建立高陡起伏的反射模型，重点讨论横向速度剧烈变化情况下高陡界面的雷达波场延拓，并从波场延拓精度与解析解、振幅保真率、高陡界面能量归位能力、成像剖面等方面着重分析不同方法的成像精度。

1  传统差分与交叉微分算子差分法

逆时偏移是波向外传播的逆过程，即倒退至零时刻的成像条件，将所有反射与绕射的能量外推至零时刻所处位置的波场^[19-20]。对于探地雷达，逆时偏移的定解问题可描述成

        (1)

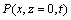其中：为介质速度，由记录的雷达波记录逆时向下延拓，传统差分法对方程(1)进行浮动变换，针对不同的起伏界面进行相应的阶乘近似：

               (2)

代入方程(1)中，得

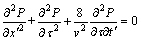           (3)

在界面陡缓程度较小的情况下，略去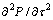，即得传统的差分偏移方程：

             (4)

交叉微分算子差分偏移法将方程(1)中的2个单微分算子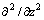和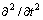改进成1个交叉微分算子，变换后方程的普遍形式可以写成：

           (5)

方程(5)未经任何近似，系数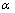由变换模式和速度参数决定。假定存在类似的交叉变换：

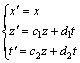                (6)

其中：系数c₁，c₂，d₁和d₂为常数。联合方程(1)和(6)得：

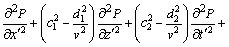
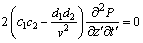           (7)

对比方程(5)和方程(7)，得

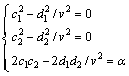            (8)

令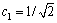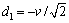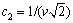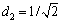，，，，即存在交叉变换：

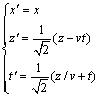                (9)

相应地，存在交叉逆变换：

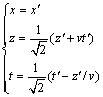              (10)

即得交叉微分算子的二阶方程：

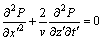              (11)

方程(11)是波动方程(1)的精确表达式，也是交叉微分算子偏移方程的定义式，未进行任何阶乘近似，可适合高陡的起伏界面偏移成像。

2  交叉微分算子偏移的波场延拓

在一维情况下，方程(1)和(11)均有如下形式：

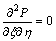                 (12)

该式的通解形式为

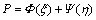             (13)

对于交叉微分算子偏移方法，在处理雷达上行波和下行波时，方程(13)有双程解，分别为 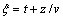和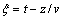，且式(13)同时具有雷达上行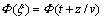波解和下行波解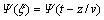，在进行波场延拓偏移时，给出边界条件：

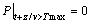              (14)

即在上行波边界条件(14)的约束下，交叉微分算子偏移方程仅有上行波解。

而对于传统的差分偏移方法，方程(13)中的变量为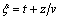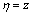，，即为

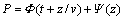           (15)

式(15)中右边第1项为上行波解，第2项为与时间无关的深度函数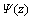，通过略去高阶微分算子，通常采用稳定的对称隐式Crank-Nicolson差分格式进行延拓。显然，尽管传统的差分偏移方法消除了下行波的影响，但是额外增加了1个与时间无关的深度函数。

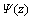传统差分偏移方法与交叉微分算子法的差分网格及波场的延拓方向分别如图1和图2所示。

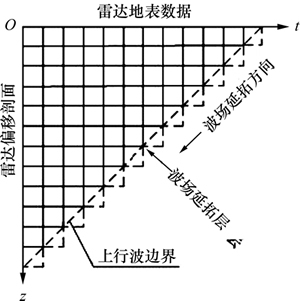
图1  传统差分偏移法的波场延拓方向

Fig. 1  Extrapolation direction of wave field in traditional difference migration algorithms

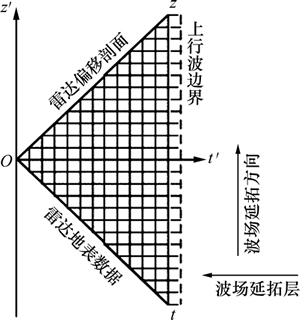
图2  交叉微分算子差分偏移法的波场延拓方向

Fig. 2  Extrapolation direction of wave field in crossed differential operator migration algorithms

在交叉变换后的坐标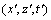下，雷达波场描述为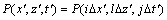，对应的交叉微分算子二阶差分格式为：

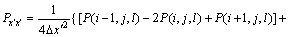
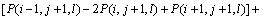
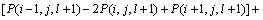
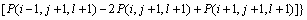(16)

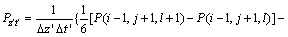
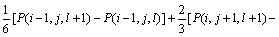
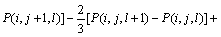
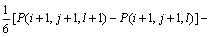
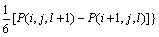         (17)

其中：；。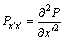

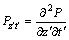得到交叉微分算子偏移方程的隐式Crank- Nicolson差分格式：

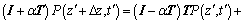
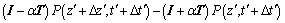(18)

其中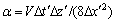：；I为以(0,1,0)为主对角元素的三对角矩阵；T为以(1-, 2, -1)为主对角元素的三对角矩阵。

3  数值算例

3.1  高陡起伏地形反射模型

为分析交叉微分算子差分偏移算法对起伏界面的延拓精度，设置1个陡缓程度差异较大的起伏地形反射模型，如图3所示。其中计算区域是1个长×宽为3.0 m×1.5 m的矩形，起伏地形的陡缓程度分别为50°和80°，高陡两侧的横向速度差异较大，介质的主要介电参数分别为：相对介电常数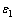=5.0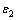，=15.0，电导率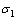=0.4 mS/m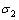，=0.2 mS/m，磁导率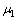=2.0 H/m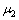，=1.0 H/m。正演计算区域的边界采用PML吸收边界条件^[20](4个方向上的边界厚度均占据5个网格)。

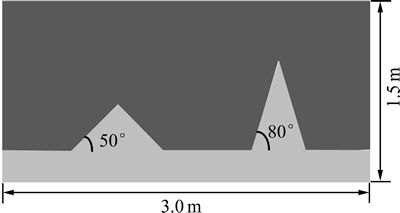
图3  高陡起伏地形的反射模型

Fig. 3  Reflection model with steep-dip rough terrains

正演计算结果如图4所示，反射模型中起伏界面的形态、陡缓程度、水平界面形态均存在不同程度的畸变，尤其是高陡界面两侧及高陡界面的顶点绕射现象严重，以致第2个高陡界面两侧的水平界面更难以分辨，且反射同相轴的振幅也存在严重缩减现象。

3.2  波场延拓精度与解析结果

波场延拓的外推精度直接影响成像质量，相邻2个高陡界面的横向距离较小，使得高陡界面的波场延拓值存在较大误差。根据初始模型中各介质的主要介电参数特征，建立相匹配的速度模型，针对第2个高陡起伏地形的左侧界面，给出了该界面附近区域的延拓结果，即为偏移剖面的第80~90道和0~15 ns区域

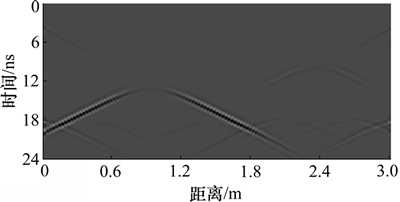
图4  高陡起伏地形反射模型的正演结果

Fig. 4  Simulation results of reflection model with steep-dip rough terrains

内不同深度的波场延拓值，结果如图5所示。

图5(a)所示为速度模型得到的理论延拓结果，将延拓值矩阵在横纵向上的长度进行归一化，计算反射同相轴的相对倾斜度，解析结果中显示的同相轴倾斜度与模型中设置的高陡界面倾角相符。图5(b)所示为传统差分偏移法的延拓结果，同相轴的相对轴倾斜度约为40°，且在高陡界面的底部，延拓结果往浅部上移，使得道集的能量并未收敛至高陡界面上，在倾斜度和道集的能量收敛方面均存在较大误差，该现象在

F-K方法所得结果中更为严重，道集的能量分布更散，如图5(c)所示，可见第80道波的9~11 ns深度范围内仍存在较大的延拓幅值。图5(d)所示为Kirchhoff法的延拓结果，计算得到的同相轴相对倾斜度约为44°，并且道集的能量收敛程度也有较大提高，但第83~87道波的9~10 ns深度上出现了“虚假”的反射同相轴。图5(e)所示为交叉微分算子差分法的延拓结果，在同相轴的相对倾斜度和道集的能量收敛方面取得了较好的平衡，且在高陡界面的底部并未出现延拓值明显较小的趋势，延拓精度大幅度提高。

3.3  振幅保真加权值

为了更细致地比较各种方法的振幅保真能力，计算模型中第2个高陡界面顶点(能量绕射聚焦点)位置的单道信号，并重点考察深度上第650~1 050个样本的振幅。

该振幅均已进行均一化处理，计算结果见图6。从图6可见：在第650~1 050个样本深度范围内，传统FD法和F-K法在信号振幅、信号位置方面取得的效果相当，Kirchhoff法则在第550~750个样本深度上的信号位置出现了偏差，信号振幅保真却比前2种略有提高，而CDO差分方法的最大振幅则约为其他3种方法的2倍，表明振幅得到了较好保真。

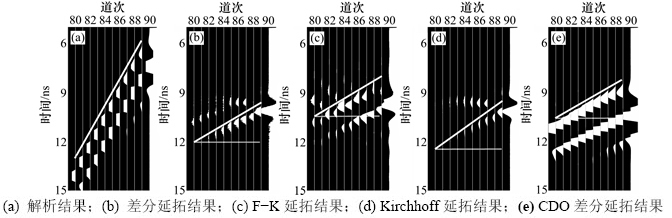
图5  高陡起伏地形的波场延拓与解析结果的对比

Fig. 5  Comparison of wavefield extrapolation in steep-dip rough terrains with analytical results using different methods

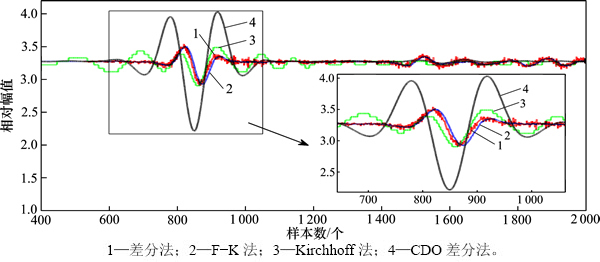
图6  不同方法在第2个高陡界面绕射点的单道波信号

Fig. 6  Trace signal of the second diffracting point in steep-dip rough interface with different methods

将延拓精度对应的解析夹角、偏移夹角和相对振幅值建立振幅保真的加权函数^[21]：

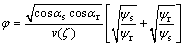       (19)

式中：；i=s, r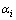；为偏移后反射界面的夹角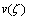；为与深度相关的速度函数。经不同偏移方法归一化的振幅与倾角的关系见图7，从图7可见：当反射界面倾角大于40°时，4种方法偏移剖面的振幅值急速下降；随界面角度继续增大，CDO方法的归一化振幅值维持在0.4左右，振幅保真值平缓地变化，体现了对高陡反射界面归位的优势。

3.4  高陡界面能量归位能力

为了更直观地比较各类偏移方法对高陡界面的能量收敛能力，将提取的各单道信号能量进行叠加堆积，得到不同偏移方法所得的剖面能量图谱，如图8所示。能量图谱显示了不同偏移方法对计算区域内绕射波的收敛能力，尤其体现了对高陡界面反射能量的归位水平。

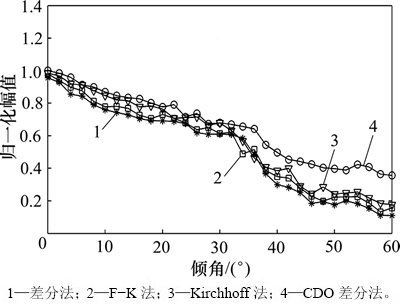
图7  不同偏移方法在不同倾角反射界面的归一化振幅曲线

Fig. 7  Normalized amplitude along different angle reflection interface with different migration method

图8(a)所示为传统差分偏移法的能量分布结果。从8(a)可见：受高陡地形的影响，第1个界面能量并未完全收敛，反射界面能量轴的附近存在能量损失，界面附近出现能量重叠的影子。该“重叠现象”同样出现在F-K偏移法所得结果中，并且在模型顶部的两端存在较明显的剩余能量，如图8(b)所示。图8(c)所示为Kirchhoff偏移法的能量分布结果，2个高陡界面的能量基本收敛，但形态模糊，界面上的能量分布较分散，表明在较精确的速度模型约束下，Kirchhoff偏移法对横向变速介质中的高陡界面具有较强的归位能力。图8(d)所示为交叉微分算子差分偏移法的能量分布结果，显然，界面上的能量均已集中，绕射顶点的能量也基本收敛，且计算区域内并未见剩余能量，高陡界面的能量归位程度较高。

3.5  成像剖面

波场延拓精度、振幅保真加权值、高陡界面能量归位能力最终影响偏移成像质量，4种偏移方法的成像结果见图9。

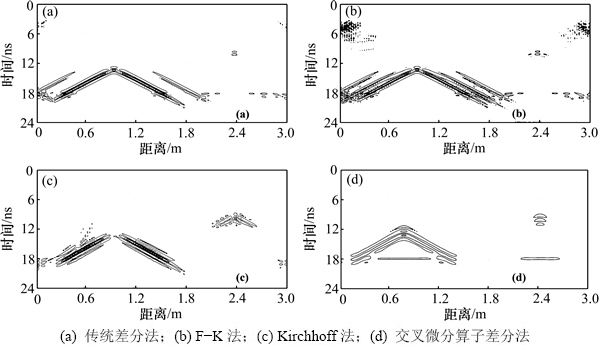
图8  不同偏移方法的能量图谱剖面

Fig. 8  Energy spectrum section with different migration methods

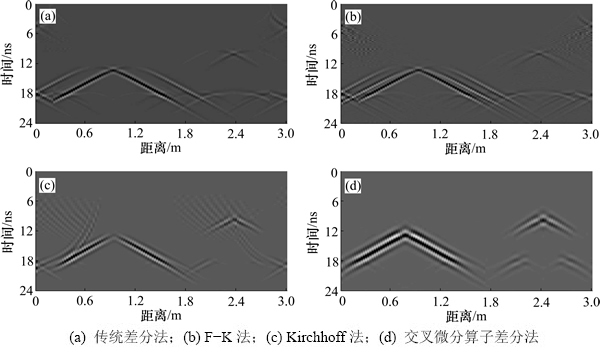
图9  不同方法的偏移成像剖面

Fig. 9  Migration imaging section with different method

图9(a)和图9(b)所示分别为传统差分法和F-K法的偏移成像剖面。从图9(a)和图9(b)可见：第1个高陡界面均基本恢复初始形态，仅顶点处产生较强绕射波并未收敛；第2个高陡界面则成像十分模糊，难以分辨。Kirchhoff法的成像剖面提高了第2个高陡界面的成像质量，基本形态能够识辨，仅在绕射界面及绕射顶点周围存在一部分散乱能量，如图9(c)所示。图9(d)所示为交叉微分算子差分法的成像剖面，2个高陡界面形态清晰，且2个顶点处能量完全收敛，还原了初始模型中高陡起伏的形态，成像质量较高。

4  结论

1) 为提高探地雷达对高陡起伏界面的偏移归位能力，将传统的单微分算子改进为交叉微分算子，提出基于交叉微分算子的差分偏移方法。该方法采用非近似的公式进行波场延拓，改变雷达波场的延拓方向，并给出交叉微分算子偏移法的波场延拓过程和相应的差分格式，避免了传统差分偏移法中略去高阶偏导。

2) 重点讨论了横向变速介质中高陡起伏地形的雷达波波场延拓算例，并从波场延拓精度与解析解、成像的振幅保真加权值、高陡界面能量归位能力和成像剖面4个方面，比较了传统差分法、F-K频率波数域法、Kirchhoff积分法和交叉微分算子差分法的偏移成像效果，分析了各类方法的成像精度。结果表明交叉微分算子差分偏移法优于传统的差分偏移法，提高了雷达波场的延拓精度，且振幅得到较好地保真，更有效地指导探地雷达高陡起伏地形的正确归位。

参考文献：

[1] FENG X, SATO M, LIU C, et al. Topographic correction of elevated GPR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 799-804.

[2] 雷林林, 刘四新, 傅磊, 等. 基于全波形反演的探地雷达数据逆时偏移成像[J]. 地球物理学报, 2015, 58(9): 3346-3355.

LEI Linlin, LIU Sixin, FU Lei, et al. Reverse time migration applied to GPR data based on full wave inversion[J]. Chinese Journal of Geophysics, 2015, 58(9): 3346-3355.

[3] CHARLES P O, MICHAEL H P, DAVID L W, et al. Improving GPR image resolution in lossy ground using dispersive migration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2492-2500.

[4] CLAERBOUT J F. Imaging the earth^’s interior[M]. Boston: Blackwell Scientific Publications, 1985: 78-92.

[5] MUFTI I R, PITA J A, HUNTLEY R W. Finite-difference depth migration of exploration-scale 3-D seismic data[J]. Geophysics, 1996, 61(3): 776-794.

[6] 冯德山, 戴前伟, 何继善. 探地雷达的正演模拟及有限差分波动方程偏移处理[J]. 中南大学学报(自然科学版), 2006, 37(2): 361-365.

FENG Deshan, DAI Qianwei, HE Jishan. Forward simulation of ground penetrating radar and its finite difference method wave equation migration processing[J]. Journal of Central South University (Science and Technology), 2006, 37(2): 361-365.

[7] COSTA C, CAMPOS I, COSTA J C, et al. Iterative methods for 3D implicit finite-difference migration using the complex Padé approximation[J]. Journal of Geophysics and Engineering, 2013, 10(4): 45011-45027.

[8] GRAY S H, MAY W P. Kirchhoff migration using eikonal equation travel time[J]. Geophysics, 1994, 59(5): 810-817.

[9] 戴前伟, 冯德山, 何继善. Kirchhoff偏移法在探地雷达正演图像处理中的应用[J]. 地球物理学进展, 2005, 20(3): 849-853.

DAI Qianwei, FENG Deshan, HE Jishan. The application of Kirchhoff’s migration method in the image processing of the ground penetrating radar forward simulate[J]. Progress in Geophysics, 2005, 20(3): 849-853.

[10] CHENG C. Three-dimensional pre-stack depth migration of receiver functions with the fast marching method: a Kirchhoff approach[J]. Geophysical Journal International, 2016, 205: 819-829.

[11] LIN L C, SHI B P, AN P. Multiwavelet prestack Kirchhoff migration[J]. Geophysics, 2016, 81(3): s79-s85.

[12] STOLT R H. Migration by Fourier transforms[J]. Geophysics, 1978, 43(1): 23-48.

[13] LOEWENTHAL D, MUFTI I R. Reversed time migration in spatial frequency domain[J]. Geophysics, 1983, 48(5): 627-635.

[14] GAZDAG J, SGUAZZERO P. Migration of seismic data by phase shift plus interpolation[J]. Geophysics, 1994, 49(1): 124-131.

[15] 贺振华, GARDNER G H. F-K波动方程偏移的频率域插值方法[J]. 石油物探, 1985, 24(1): 1-22.

HE Zhenhua, GARDNER G H. Interpolation in the Fourier transform domain with applications to F-K migration[J]. Geophysical Prospecting for Petroleum, 1985, 24(1): 1-22.

[16] SUN R, MCMECHAN G A. Scalar reverse-time depth migration of prestack elastic seismic data[J]. Geophysics, 2001, 66(5): 1519-1527.

[17] DAVYDENKO M, VERSCHUUR D J. Full-wavefield migration: using surface and internal multiples in imaging[J]. Geophysical Prospecting, 2016, 64(2): 505-513.

[18] 傅磊, 刘四新, 刘澜波, 等. 机载探地雷达数值模拟及逆时偏移成像[J]. 地球物理学报, 2014, 57(5): 1636-1646.

FU Lei, LIU Sixin, LIU Lanbo, et al. Airborne ground penetrating radar numerical simulation and reverse time migration[J]. Chinese Journal of Geophysics, 2014, 57(5): 1636-1646.

[19] BAYSAL E, KOSLOFF D D, SHERWOOD J W C. Reverse- time migration[J]. Geophysics, 1983, 48(11): 1514-1524.

[20] BERENGER J P. A perfectly matched layer for the absorption of electromagnetic-waves[J]. Journal of Computational Physics, 1994, 114: 185-200.

[21] EKREN B O, URSIN B. True-amplitude frequency-wavenumber constant offset migration[J]. Geophysics, 1999, 64: 915-924.

(编辑  陈灿华)

收稿日期：2016-03-14；修回日期：2016-05-15

基金项目(Foundation item)：国家自然科学基金资助项目(41374118，41574116)；中国铁路总公司科技研究开发计划项目(2014G005-B)；湖南省交通科技计划项目(201423)；湖南省住房和城乡建设厅科技计划项目(BZ201408，BZ201411)；中南大学创新驱动项目(2015CX008) (Projects(41374118, 41574116) supported by the National Natural Science Foundation of China; Project(2014G005-B) supported by the Key Program of Science and Technology of China Railway Corporation; Project(201423) supported by the Traffic Department of Science and Technology Program of Hunan Province; Projects(BZ201408, BZ201411) supported by the Science and Technology Plan of Housing and Construction Department of Hunan Province; Project(2015CX008) supported by Innovation-Driven Plan of Central South University)

通信作者：尹小波，教授，从事浅层地球物理试验检测方法及理论研究；E-mail: yinxiaobo@csu.edu.cn