文章编号:1004-0609(2016)-12-2640-07
基于光滑约束的磁梯度张量3D正则化反演方法
李金朋,张英堂,李志宁,范红波,尹 刚
(解放军军械工程学院 七系,石家庄 050003)
摘 要:针对铁磁物质反演方法中反演解的病态性问题,提出基于光滑约束的磁梯度张量3D正则化反演方法。首先,利用积分灵敏度矩阵和粗糙度矩阵对经典Tikhonov正则化理论框架下的反演模型进行约束,避免由于反演参数多于采集点数而导致的不稳定;然后,通过定义正则化修正系数确定合理的初始正则化因子,从而减少因正则化因子引入而在反演结果中介入的误差;最后,利用物性参数上下限约束函数,将反演过程中的解转换到合理的值域范围内,得到与原始模型更加吻合的反演结果。仿真及实验结果表明:该反演方法能够准确还原磁性异常体的轮廓形态,具有较好的横向和纵向分辨率。
关键词:光滑约束;磁梯度张量;积分灵敏度矩阵;粗糙度矩阵;正则化因子
中图分类号:P631 文献标志码:A
磁性目标反演技术是通过地面或航空等实测数据利用某种手段推算出磁性体(未爆弹、水雷、潜艇等)物性参数在地下的分布规律从而达到寻找磁性体的目的[1]。根据反演方法的不同将反演分为物性反演和形态反演两类。其中基于磁场信息的物性反演方法因具有探测精度高、虚警率低、定位能力强等优点得到了较为广泛的关注,逐渐成为军事侦察,水文及工程地质勘探等领域的关键技术。磁梯度张量场是指磁场三分量在3个坐标方向上的变化率,共有9个分量。相比磁总场、磁总场梯度和磁场三分量数据,磁梯度张量场具有更高的分辨率,能更好地描绘地下小尺度磁性体的空间形态及位置[2-6]。
在磁梯度张量数据三维反演方法中,反演结果的多解性主要是由于反问题的病态性引起的。TIKHONOV等[7-8]和ZHDANOV[9]指出在反演过程中通过加入正则化参数重新构造目标函数,从而达到获得稳定解的目的;WILSON等[10]利用获得的航空重力梯度测量数据,采用共轭梯度法进行反演;LI[11]提出了基于平滑约束的重力梯度张量数据反演方法,并应用于实测资料,取得良好的效果;吴小平[12]提出将共轭梯度法应用于电阻率三维反演中,并讨论了不同正则化因子对反演结果的影响;朱自强等[13]利用混合正则化反演方法,减弱了反演的聚焦效应,能有效获得异常边界;杨娇娇等[14]通过向目标函数中引入深度加权函数来提高对目标深度信息的识别能力。上述文献研究方法为磁梯度张量反演提供了较好的研究思路,但是所得反演成像结果存在“趋肤效应”,同时正则化因子的选取常采用经验定值方法,导致计算精度较低,难以达到最佳的拟合效果。针对此问题,本文作者提出基于光滑约束的磁梯度张量3D正则化反演方法,首先,利用积分灵敏度矩阵和粗糙度矩阵解决反演过程中的病态解问题;然后,通过定义正则化修正系数减少介入误差提高拟合精度;最后,引入物性参数上下限约束函数将反演结果转换到合理的值域内,得到与原始模型更加吻合的反演结果。
1 磁梯度张量三维反演理论
磁梯度张量正演公式表示为
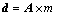 (1)
(1)
式中:矩阵A的元素Aij为第i(i=1, 2, 3, …, p)个观测点观测的第j (j=1, 2, 3, …, n)个单元的响应;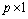 维的行向量d为任意张量分量数据;m为反演物性参数。
维的行向量d为任意张量分量数据;m为反演物性参数。
根据Tikhonov正则化理论,构建三维目标函数:
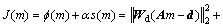
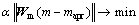 (2)
(2)
式中: 为数据拟合泛函;
为数据拟合泛函;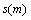 通常为L1或L2罚项即模型约束泛函;离散情况下
通常为L1或L2罚项即模型约束泛函;离散情况下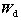 和
和 分别为数据和模型的加权矩阵;
分别为数据和模型的加权矩阵;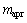 为模型先验信息;
为模型先验信息;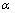 为正则化因子。
为正则化因子。
2 光滑约束正则化理论
在反演过程中,由于重构模型的核函数随深度快速衰减,因此导致反演结果产生“趋肤效应”。为了解决这一问题,利用积分灵敏度矩阵S对模型进行加权。观测数据与模型参数的变化可以表示为
 (3)
(3)
式中: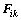 为观测数据关于参数的灵敏度。
为观测数据关于参数的灵敏度。
数据灵敏度对模型mk的积分可以表示为
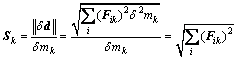 (4)
(4)
故积分灵敏度矩阵S为对角矩阵:
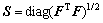 (5)
(5)
定义粗糙度矩阵R为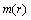 在x, y和z方向的一阶偏微分的平方和,即
在x, y和z方向的一阶偏微分的平方和,即
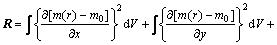
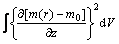 (6)
(6)
对应的Tiknonov正则化方程(2)变为
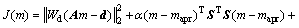
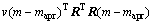 (7)
(7)
式中:v为粗糙度矩阵的权重系数,数量级范围在10-8~10-9之间。
利用共轭梯度法对目标函数进行求解,式(7)可以改写为方程组:
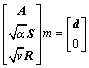 (8)
(8)
则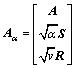 代表雅克比矩阵,
代表雅克比矩阵, ,式(8)可改写为
,式(8)可改写为
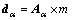 (9)
(9)
具体算法实施步骤如下:
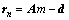 ,
,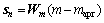 ,
,
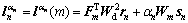
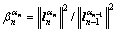 ,
,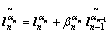 ,
,
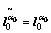
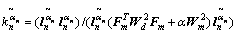
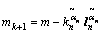
式中:n为当前迭代次数;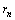 为数据拟合残差;m为模型参数;
为数据拟合残差;m为模型参数;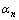 为正则化因子;sn为模型稳定项;Fm为偏导数矩阵;
为正则化因子;sn为模型稳定项;Fm为偏导数矩阵; 为共轭梯度方向;
为共轭梯度方向;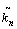 为步长。
为步长。
2.1 自适应正则化参数的选择
本文在传统的自适应的正则化算法基础上引入了正则化修正系数提高反演精度:
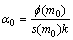 ,
,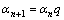 (10)
(10)
式中:k正则化修正系数;q为衰减因子;m0为物性参数初值。ZHDANOV[9]指出衰减因子q的取值范围为[0.5, 0.9],但是并未指出一种明确的衰减机制。
定义一个长方体模型,尺寸为5 m×4 m×4 m,长方体中心坐标为(11, 11, 5)。测区范围是21 m×21 m。在仅考虑感应磁化条件下,异常体的磁化强度为40 A/m,磁倾角为70°,磁偏角为20°。设置最高迭代次数为60次。为确定自适应正则化的各部分参数:
定义逼近误差函数:
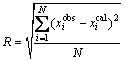 (11)
(11)
式中:N为观测点总数;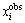 为实际值;
为实际值;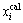 为理论值。
为理论值。
图1(a)所示为各个分量在不同迭代次数下的逼近误差。由图1(a)可知,随迭代次数增加,各分量的拟合误差逐渐减小,其中Ayz和Azz分量迭代过程相比其他分量较为稳定,而且收敛速度较快。由图1(b)可以看出,各分量k值在10到50之间的模型逼近情况较好。图1(c)可以看出,当q在[0.8, 0.9]区间时,模型逼近误差小,拟合效率更好。综合以上因素,设置q为0.9,k为10,选取Azz进行单分量反演。利用光滑约束进行处理,处理结果如图2(a)和图2(c)所示。根据图像可以看出,反演结果具有较好的横向和纵向分辨率,与之相比如果不进行光滑约束处理,异常体分布于地表附近,其纵向分辨率很差(见图2(b)和2(d))。
2.2 物性参数分布的上下限约束函数
KIM等[15]通过对数约束实现了将电导率限制在合理的值域目标中。CARDARELLI等[16]将对数转换方法成功应用于电阻率层析成像中[16]。本研究使用的上下限约束函数[17]如下所示:
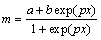 ,
,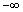 <x<
<x<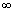 (12)
(12)
式中:a和b分别为强制约束边界的上下限。通过图3可以看出,p值反映出物性参数转换的速度。p值取0.5~1之间可以使反演结果较为合理的转换到符合地球物理意义的数值范围。处理实测数据时,将反演结果视为式(12)中的x,通过该式可以实现反演数据的上下限约束。
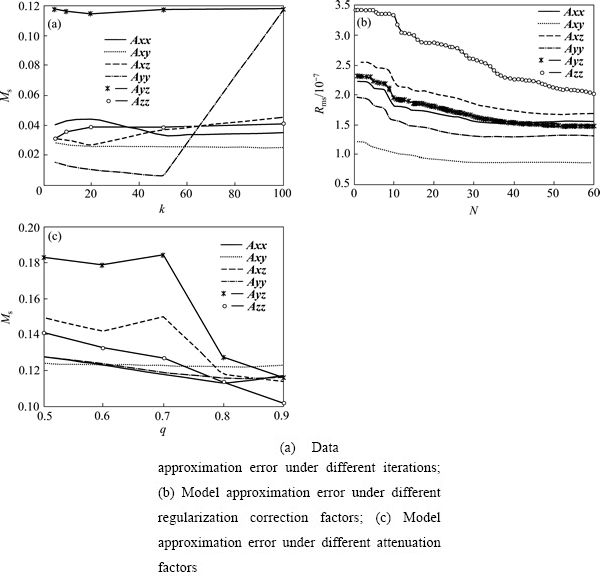
图1 各分量不同参数选取方案的数据统计
Fig. 1 Statistics of different parameters program for each component
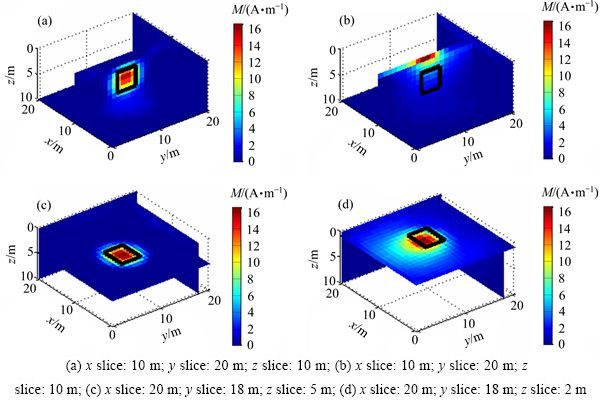
图2 单直立长方体单分量反演结果切片图
Fig. 2 Inversion slice of cuboid single component
3 仿真分析
为验证本文方法的有效性,设计包含了两个异常体的组合模型进行三维测试。将地下待测空间划分为21×21×10=4410个单元格,每个单元格均为边长为1 m的正方体,地面的观测点为21×21=441个网格。在仅考虑感应磁化的条件下异常体由两个长方体组成,其中长方体1的中心坐标为(6, 10.5, 4),尺寸为5 m×4 m×4 m;长方体2的中心坐标为(13, 10.5, 4),尺寸为9 m×8 m×6 m,假设磁化倾角为70°,磁化偏角为20°,磁化强度为40 A/m。
地下正演模型如图4所示,图4(a)所示黑色部分表示待测异常体,箭头表示磁化方向,切片图为模型在待测平面上产生的磁总场异常数据平面图;图4(b)表示待测异常体产生的理论磁梯度张量数据,从磁梯度张量各分量云图可以看出,Azz分量正极值与待测异常体水平位置具有良好的对应关系,而且通过前面讨论可知Azz分量在计算过程中具有良好的稳定性,由此,本文作者利用磁梯度张量Azz数据并加入5%的高斯噪声作为实测数据进行反演。反演的物性参数分布在不同切面处的分布特点如图5所示,反演过程中设置最高迭代次数为55次,k为50,q取0.9。黑色框所圈定的范围是正演组合模型体所在位置及分布范围,从图5中结果可以看出:反演方法能够较好地反映长方体组合模型的轮廓形态,具有较好的横向和纵向分辨率。
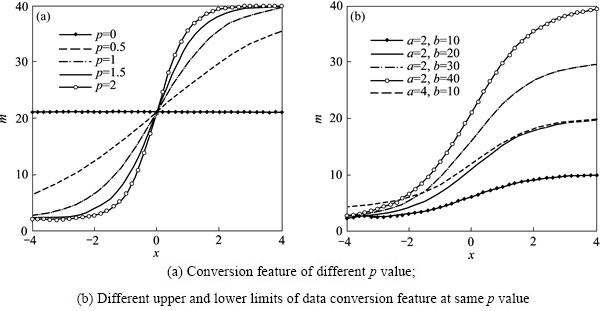
图3 上下限约束特征中参数变化对转换空间值的影响
Fig. 3 Influence of change of parameter on transform space in upper and lower function
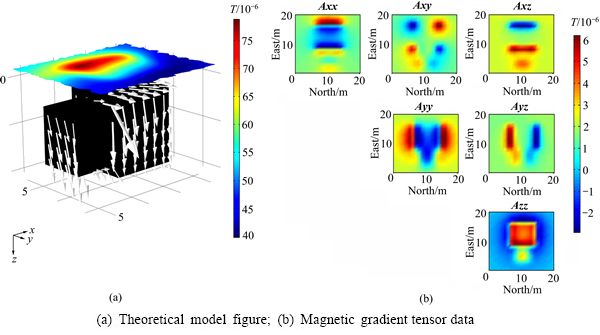
图4 组合模型三维空间形态及磁梯度张量数据平面图
Fig. 4 Three-dimensional shade of model and magnetic gradient tensor data plan
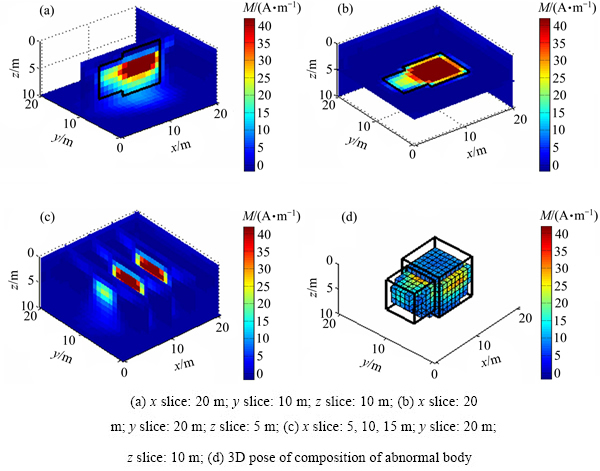
图5 组合异常体反演切片图及三维姿态
Fig. 5 Inversion slices and 3D pose of composition of abnormal body
4 实测资料验证
由于地理环境和测量误差的影响,会导致实际测量的磁梯度张量数据精度下降。选择垂向和水平分辨率相对较高的Azz分量进行方法的有效性验证。测区位于石家庄某地,侧区内放置一个南北走向的未爆弹,其直径约20 cm,沿x轴坐标为0.5~1.3 m,未爆弹的轴线距离观测面0.5 m。图6展示了测量台架及传感器阵列图,将待测空间划分为22×22×10=4840个单元格,每个单元格均为边长为0.1 m的正方体,地面的观测点为22×22=484个网格。图7所示为未爆弹的实测磁梯度张量数据,反演过程中设置最高迭代次数为55次,k为50,q取0.9。
反演结果如图8所示,根据反演结果可以看出,本方法所得反演结果与未爆弹的位置及轮廓相吻合,进一步证明本方法的有效性。

图6 实测区域及传感器阵列
Fig. 6 Actual measurement area and sensor array
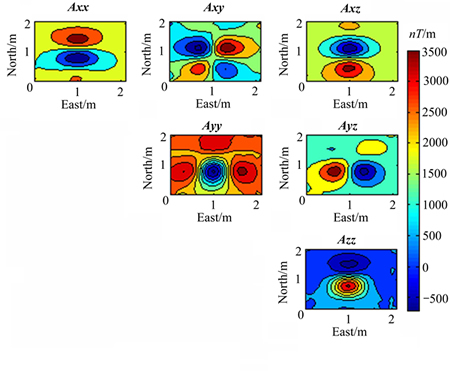
图7 实测未爆弹磁梯度张量数据
Fig. 7 Magnetic gradient tensor data of UXO
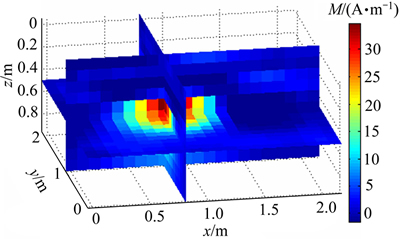
图8 反演结果图
Fig. 8 Inversion result slice
5 结论
1) 提出的光滑约束正则化反演方法能很好的压制反演结果的“趋肤效应”,提高3个方向的分辨率,使反演结果呈现出平滑结构。
2) 提出改进的自适应正则化方法,通过确定合理的正则化因子,提高反演的精度及稳定性。
3) 引入上下限约束函数,深入讨论了参数的选择及设定的原则,该函数可以将不具有实际物理意义的反演结果转化到合理的范围,给进一步解释工作带来方便。
4) 通过仿真及实验验证,证明利用共轭梯度法对目标函数进行求解,能够准确地反演出异常体的空间姿态及物性参数特征。
REFERENCES
[1] 陈召曦, 孟小红, 郭良辉. 重磁数据三维物性反演方法进展[J]. 地球物理学进展, 2012, 27(2): 503-511.
CHEN Zhao-xi, MENG Xiao-hong, GUO Liang-hui. Review of 3D property inversion of gravity and magnetic data[J] . Progress in Geophysics, 2012, 27(2): 503-511.
[2] 卞光浪, 翟国军, 黄谟涛. 顾及地磁背景场的多目标磁异常分量换算方法[J]. 武汉大学学报, 2011, 36(8): 914-918.
BIAN Guang-lang, ZHUAI Guo-jun, HUANG Mo-tao. Transformation of multiobjects magnetic anomaly components with geomagnetic effect[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 914-918.
[3] 张昌达. 航空磁力梯度张量测量—航空磁测技术的最新进展[J]. 工程地球物理学报, 2007, 3(5): 354-361.
ZHANG Chang-da. Airborne tensor magnetic gradiometry—the latest progress of airborne magnetomeric technology[J]. Chinese Journal of Engineering Geophysics, 2007, 3(5): 354-361.
[4] 石 磊, 郭良辉, 孟小红. 磁总场异常垂直梯度三维相关成像[J]. 地球物理学进展, 2012, 27(4): 1069-1614.
SHI Lei, GUO Liang-hui, MENG Xiao-hong. 3D correlation imaging of the vertical gradient of magnetic total field anomaly[J]. Progress in Geophysics, 2012, 27(4): 1069-1614.
[5] 吴招才. 磁力梯度张量技术及其应用研究[D]. 武汉: 中国地质大学, 2008.
WU Zhao-cai. Magnetic gradient tensor technology and its application[D]. Wuhan: China University of Geosciences, 2008.
[6] 孟 慧. 磁梯度张量正演、延拓、数据解释方法研究[D]. 吉林: 吉林大学, 2012.
MENG Hui. Forward modeling, continuation and data interpretation of magnetic gradient tensor[D]. Jilin: Jilin University, 2012.
[7] TIKHONOV A N, ARSENIN V Y. Solution of Ill-posed problems[M]. New York: V.H. Winston & Sons, 1997.
[8] TIKHONOV A N. Regularization of Ill-posed problems[J]. Doklady Akad, 1963, 153: 49-52.
[9] ZHDANOV M S. Geophysical inverse theory and regularization problems[M]. New York: Elsevier Science, 2002.
[10] WILSON G, CUMA M, ZHDANOV M S. Massively parallel 3D inversion of gravity and gravity gradiometer data[J]. Preview, 2011, 152(6): 29-34.
[11] LI Y. 3-D inversion of gravity gradiometer data[C]// 2001 SEG Annual Meeting, SEG Technical Program Expanded Abstracts. San Antonio: Society of Exploration Geophysicists, 2001: 1470-1473.
[12] 吴小平. 利用共轭梯度法的电阻率三维反演若干问题研究[J]. 地震地质, 2001, 23(12): 321-327.
WU Xiao-ping. Study on some problems for 3d resistivity inversion using conjugate gradient[J]. Seismology and Geology, 2001, 23(12): 321-327.
[13] 朱自强, 曹书锦, 鲁光银. 基于混合正则化的重力场约束反演[J]. 中国有色金属学报, 2014, 24(10): 2601-2608.
ZHU Zi-qiang, CAO Shu-jin, LU Guang-yin. 3D gravity inversion with bound constraint based on hyper-parameter regularization[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2601-2608.
[14] 杨娇娇, 刘 展, 陈晓红, 徐凯军. 基于深度加权的重力梯度张量数据的3D聚焦反演[J]. 世界地质, 2015, 34(1): 210-218.
YANG Jiao-jiao, LIU Zhan, CHEN Xiao-hong, XU Kai-jun. Three-dimensional focusing inversion of gravity gradient tensor data based on depth weighting[J]. Global Geology, 2015, 34(1): 210-218.
[15] KIM H J, SONG Y, LEE K H. Inequality constraint in least-squared inversion of geophysical data[J]. Earth Planets Space, 1999, 51: 255-259.
[16] CARDARELLI E, FISCHAGER F. 2D data modelling by electrical resistivity tomography for complex subsurface geology[J]. Geophysical Prospecting, 2006, 54(2): 121-133.
[17] COMMER M, NEWMAN G A. New advances in three- dimensional controlled-source electromagnetic inversion[J]. Geophysical Journal International, 2008, 172(2): 513-535.
3D magnetic gradient tensor regularization inversion method based on smooth constrained
LI Jin-peng, ZHANG Ying-tang, LI Zhi-ning, FAN Hong-bo, YIN Gang
(Seventh Department, Ordnance Engineering College, Shijiazhuang 050003, China)
Abstract: For the ill-posed problem of ferromagnetic materials inversion method, the method based on 3D magnetic gradient tensor regularization inversion method was proposed based on smooth constraint condition. First, the unstable defect caused by the number of inverse parameter far than observational points by using the integral sensitivity matrix and the roughness matrix in the classical Tikhonov regularization under the framework of the theory to constrain the model is avoided. Then, errors are reduced due to regularization factor introduced in the inversion results, by defining regularization correction factor to determine a reasonable initial regularization factor. Finally, by using the upper and lower constraint function of physical parameters, the solution to a reasonable value range in the inversion process is converted and the inversion results which are more consistent with the original model are obtained. Simulation and experimental results show that this inversion method can reflect the outline shade of the magnetic anomaly, and has good lateral and vertical resolution.
Key words: smooth constraint; magnetic gradient tensor; integral sensitivity matrix; roughness matrix; regularization factor
Foundation item: Project(51305454) supported by the National Natural Science Foundation of China
Received date: 2015-11-23; Accepted date: 2016-04-17
Corresponding author: ZHANG Ying-tang; Tel: +86-311-87994748; E-mail: zyt01@mails.tsinghua.edu.cn
(编辑 王 超)
基金项目:国家自然科学基金资助项目(51305454)
收稿日期:2015-11-23;修订日期:2016-04-17
通信作者:张英堂,教授,博士;电话:0311-87994748;E-mail: zyt01@mails.tsinghua.edu.cn