基于损伤理论的混凝土双轴压本构模型
商怀帅1, 2,杨鲁生3
(1. 青岛理工大学 土木工程学院, 山东 青岛,266033;
2. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连,116023;
3. 潍坊市市政工程建设处,山东 潍坊,261031)
摘要:对快速冻融循环作用后的普通混凝土进行双轴压试验研究,测得其双轴压应力-应变关系曲线。根据Weibull统计分布理论和等效应变假定原理,建立基于损伤理论并考虑应力比影响的普通混凝土双轴压本构模型。研究结果表明:该模型可以有效地描述双轴压荷载作用下普通混凝土的本构关系。
关键词:混凝土;冻融循环;双轴压;损伤理论;本构模型
中图分类号:TU375 文献标志码:A 文章编号:1672-7207(2013)01-0340-05
Constitutive model of damage of concrete under biaxial compression
SHANG Huaishuai1, 2, YANG Lusheng3
(1. School of Civil Engineering, Qingdao Technological University, Qingdao 266033, China;
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116023, China;
3. Engineering Construction Department of Weifang Municipal, Weifang 261031, China)
Abstract: The strength experiments of plain concrete after freeze-thaw cycles under biaxial compression were studied. The stress-strain relationship of specimens after freeze-thaw cycles was measured. On the basis of damage model of concrete under uniaxial compression, the constitutive model of damage was founded according to the Weibull distribution phenomenological method and equivalent strain hypothesis theory considering the stress ratio of concrete under biaxial compression. The results show that the given model can describe the mechanical capability of plain concrete under biaxial compression after freeze-thaw cycles.
Key words: concrete; freeze-thaw cycles; biaxial compression; damage theory; constitutive model
强度和耐久性是混凝土结构的2个重要指标。混凝土的耐久性是使用期内混凝土保证正常功能的能力,关系结构物的使用寿命。而冻融循环作用是影响普通混凝土耐久性的一个十分重要的因素。北方寒冷地区的许多已建工程在实际使用过程中,由于受环境气候的影响,或多或少地存在混凝土被冻融破坏,并且这些结构一般处于复杂应力状态下:因此,研究冻融循环作用后普通混凝土在多轴应力状态下的变形特性,对于合理的结构设计具有重要意义。由于试验操作困难,目前,国内外对这方面的研究工作集中在研究冻融循环后普通混凝土的质量损失、动弹性模量的变化,而关于其在多轴应力状态下变形特性的研究很少。随着计算机技术的迅速发展, 有限元法在混凝土和钢筋混凝土结构分析中得到广泛应用,迫切需要建立冻融循环作用后普通混凝土在多轴应力状态下的本构关系。混凝土本构关系就是混凝土应力与应变关系[1],混凝土在单轴应力状态下的本构关系即单轴受拉、单轴受压时的应力-应变关系比较明确,可以通过试验测定。并且很多学者根据不同的方法,提出了多种不同的表达式[2-6]。混凝土在多轴应力状态的本构关系[1-6]比单轴本构关系要复杂得多。在多轴应力状态下,各方向的正应变和横向变形效应互相约束、牵制,影响内部裂缝的出现和扩展。而且多轴压荷载作用下的混凝土强度成倍增大,多轴拉-压荷载作用下的混凝土强度有所降低,扩大了混凝土的应力范围,也改变了各部分变形的比例,出现了不同的破坏过程和形态,这些都使得多轴荷载作用下混凝土的变形趋于复杂。另一方面,由于多轴试验设备复杂,试验难度大,变形量测技术难度大,使得多轴本构曲线的获得难度加大。为此,本文作者针对我国北方寒冷地区的公路、桥涵、港口码头等设计中遇到的双轴应力作用下普通混凝土的变形性能开展了试验研究,按照现行的GB/T 50082—2009[7]中的抗冻性能试验中的快冻法,对经受快速冻融循环作用的普通混凝土在双轴压荷载作用下进行试验研究,测试2个加载方向的应力-应变关系曲线,以便为处于寒冷地区的桥涵、混凝土路面、港口码头和城市立交桥等建筑物的工程设计及非线性有限元分析提供可靠的试验依据。基于混凝土多轴本构关系对于结构的设计以及有限元分析非常重要,人们进行了大量的试验研究和理论分析,提出了多种多样的混凝土本构关系,这些本构模型的理论基础、观点和方法迥异,使用范围和计算结果差别很大。本文作者依据损伤理论并同时考虑应力比影响,建立双轴压荷载作用下混凝土的本构模型。
1 试验设计
1.1 试件制作及快速冻融试验方法
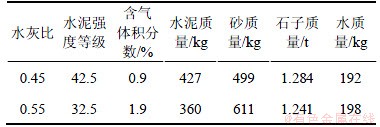
本试验配制了水灰比为0.45和0.55的普通混凝土试块,具体制作方法见文献[8]。表1所示为每立方米混凝土的配合比及性能指标。
试件制作24 h后拆模,随后在标准条件下养护23 d,再将试件放在温度为15~20 ℃的水中浸泡4 d。本文的快速冻融循环试验在大连理工大学海岸与近海工程国家重点实验室的混凝土快速冻融试验机(TDR1)上进行,试验严格按照GB/T 50082—2009中的快冻法执行。
表1 每立方米混凝土的配合比及性能指标
Table 1 Mix proportion of concrete in per cubic meter concrete and characteristics of concrete
1.2 试验设备及过程
本文的力学性能试验在大连理工大学海岸与近海工程国家重点实验室自行研制的大型静、动三轴电液伺服试验机[9]上进行。由于冻融循环作用,试件表面有凹有凸,所以,在进行力学性能试验前,要对试件表面进行机械磨面;由于试验采用的是受压面积为100 mm×100 mm的小试件,试验时两端的摩擦对混凝土抗压强度的影响较大,因此,采用三层塑料薄膜中间涂少许甘油这种减摩擦方式应用于试件受压面。试验加载速度控制在0.2~0.5 MPa/s。
2 双轴压损伤本构模型
损伤力学是近几十年迅速发展起来的一门新学科。1958年,Kachanov[10]提出用连续度来描述材料的逐渐衰变,使得材料中复杂的、离散的衰变破坏过程可以用1个连续变量来描述。作为一个理论体系,损伤力学是从20世纪70年代才开始建立并得到逐步发展的。期间,Lemaitre[11]的研究工作为损伤理论的形成和发展作出了重要贡献。
在外载和环境荷载作用下,由于细观结构层次的微缺陷发展引起的材料或结构的劣化过程称为损伤。余天庆等[12]基于对混凝土破坏机理和力学性质的研究,认为损伤理论比较适合于混凝土研究;这是因为:(1) 混凝土的损伤过程(开裂过程)可以看作是连续的,并且在很小的应力或应变下就已发生;(2) 裂缝的扩展方向几乎与最大主应力方向垂直;(3) 外界作用以前存在的缺陷可以作为初始损伤处理。自从Dougill等[13]将损伤力学概念应用于混凝土的研究以来,许多研究者对混凝土损伤理论进行了研究和实践应用,如王春来等[14]利用损伤本构模型对单轴受压状态下钢纤维混凝土的应力-应变关系进行了描述。本文在单轴压损伤模型的基础上,引入双轴压应力比,建立普通混凝土在双轴压荷载作用下的损伤本构模型。
在双轴压荷载作用下的混凝土试件,对于一给定的主压向应力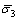 ,其相应的主压向应变
,其相应的主压向应变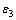 受到次压向应力
受到次压向应力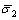 的影响。基于此,在建立双轴荷载作用下混凝土的本构关系时,应当考虑应力比对模型的影响。因此,主压向应变用下式表示:
的影响。基于此,在建立双轴荷载作用下混凝土的本构关系时,应当考虑应力比对模型的影响。因此,主压向应变用下式表示:
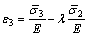 (1)
(1)
式中: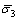 和
和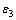 分别为主压向的应力和应变;
分别为主压向的应力和应变;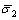 为次压向应力;
为次压向应力;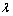 为泊松比(本文中令
为泊松比(本文中令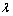 =0.2);E为弹性模量。将应力比
=0.2);E为弹性模量。将应力比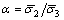 代入式(1)得到:
代入式(1)得到:
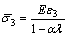 (2)
(2)
根据应变等效原理,受损材料的任何应变本构关系可以从无损材料的本构方程导出,只要用损伤后的有效应力来取代无损材料本构关系中的名义应力即可。设由于材料内部损伤,实际承担载荷的未受损区等效阻力体积为Vn,损伤区的体积为Vd,总体积为V,则损伤变量D=Vd/V,根据V=Vd+Vn,可得有效应力为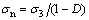 ,即
,即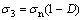 ,由此得到双轴压荷载下混凝土主压向本构关系为:
,由此得到双轴压荷载下混凝土主压向本构关系为:
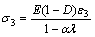 (3)
(3)
本文作者认为双轴压荷载作用时的材料强度服从Weibull 统计分布,材料的损伤变量D也服从该统计分布,根据二参数的Weibull 分布,有
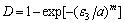 (4)
(4)
式中:m≥0,为形状参数;a≥0,为尺度参数。
根据连续损伤力学基本关系公式,将式(4)代入式(3)得:
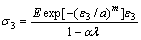 (5)
(5)
根据双轴压荷载作用下,混凝土试件应力-应变全曲线的特点,参数a和m根据以下条件决定:
(1) 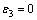 ,
, ;
;
(2) 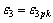 ,
,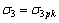 ;
;
(3) 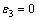 ,
,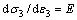 ;
;
(4) 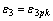 ,
,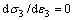 。
。
其中: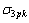 和
和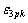 分别为双轴压荷载作用下的峰值应力和峰值应力对应的应变。
分别为双轴压荷载作用下的峰值应力和峰值应力对应的应变。
对式(5)的应变求导,则有:
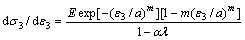 (6)
(6)
将边界条件代入式(6)可得:
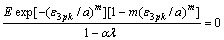 (7)
(7)
由式(7)得到:
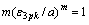 (8)
(8)
整理式(8)得到尺度参数为:
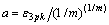 (9)
(9)
将式(9)代入式(3)得到形状参数为:
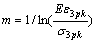 (10)
(10)
将式(9)代入式(4),并根据双轴压曲线应满足的条件可以得到损伤变量为:
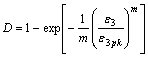 (11)
(11)
式(11)即为混凝土材料在双向受压荷载下的损伤演化方程。由式(11)可知:损伤变量D仅与当前材料在双轴压荷载作用下的应变、初始弹性模量、峰荷应变以及峰值应力有关。最后得到基于损伤理论并同时考虑应力比影响的双轴压本构模型为:
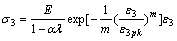 (12)
(12)
当水灰比为0.55的混凝土经过0,25和50次冻融循环作用,且应力比α为0.25和0.50时,实测的双轴压主应力方向的应力-应变关系曲线与利用损伤本构方程求得的计算曲线如图1所示。从图1可见:本文模型的计算结果与试验结果较吻合。
此外,对于双轴压作用下水灰比为0.45的普通混凝土,利用本文的双轴压损伤本构模型对应力比α=0.75时主压向的应力-应变关系进行计算,结果见图2。其中, 为不同冻融循环次数下混凝土试样的主压向应力。从图2可见:本文模型能较好描述冻融循环前后该应力比条件下混凝土的应力-应变曲线。
为不同冻融循环次数下混凝土试样的主压向应力。从图2可见:本文模型能较好描述冻融循环前后该应力比条件下混凝土的应力-应变曲线。
将文献[15]中经受不同冻融循环作用的普通混凝土的双轴压试验值与本文模型的计算值进行对比,见图3。从图3可见:试验值与计算值也较吻合。
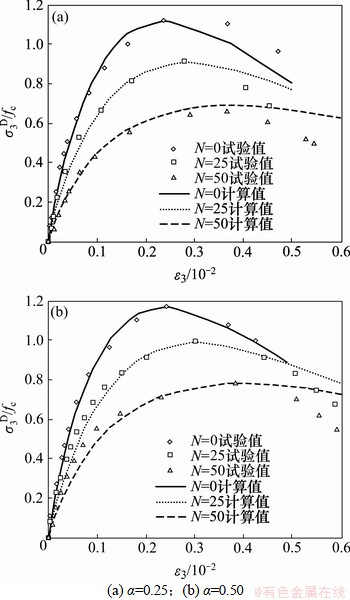
图1 水灰比η为0.55时双轴压时主压向应力-应变关系曲线与损伤理论曲线
Fig.1 Comparison of theoretical curves with test curves between stress and strain under biaxial compression whenη is 0.55
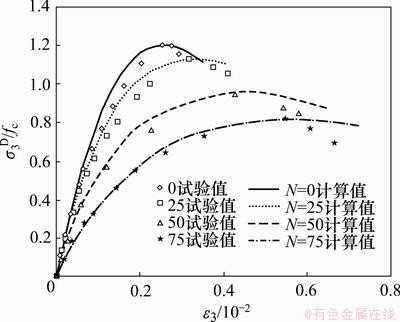
图2 水灰比η为0.45, α=0.75时双轴压主压向应力-应变关系曲线与损伤理论曲线
Fig.2 Comparison of theoretical curves with test curves between stress and strain under biaxial compression whenη is 0.45 and α is 0.75
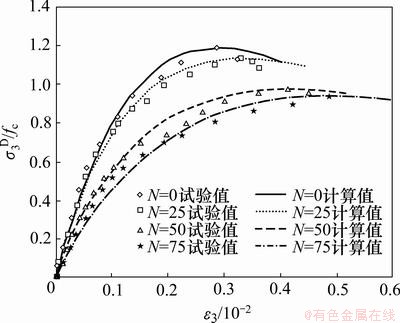
图3 水灰比η为0.50, α=1.00时双轴压主压向应力-应变关系曲线与损伤理论曲线
Fig.3 Comparison of theoretical curves with test curves between stress and strain under biaxial compression whenη is 0.50 and α is 1.00
3 结论
(1) 对经历不同冻融循环次数作用后普通混凝土试件进行了双轴压试验研究,测得不同冻融循环次数作用后的普通混凝土的双轴压应力-应变关系曲线。
(2) 将损伤理论引入双轴压本关模型的分析中,根据Weibull统计分布理论和等效应变假定原理,建立了不同冻融循环次数作用下基于损伤理论并考虑应力比影响的双轴压本构模型。该模型能很好地描述不同冻融循环次数作用后的普通混凝土在双轴压荷载下应力-应变关系。
参考文献:
[1] 宋玉普, 赵国藩,靳国礼, 等.平面应变状态下的混凝土变形和强度特性[J]. 水利学报, 1990, 21(5): 22-29.
SONG Yupu, ZHAO Guofan, JIN Guoli, et al. Behaviors of deformation and strength of concrete under plane strain condition[J]. Journal of Hydraulic Engineering, 1990, 21(5): 22-29.
[2] 江见鲸. 钢筋混凝土结构非线性有限元分析[M]. 西安: 陕西科学技术出版社, 1994: 24-180.
JIANG Jianjing. Nonlinear finite element analysis of reinforced concrete[M]. Xi’an: Shanxi Science and Technology Press, 1994: 24-180.
[3] 朱伯龙, 董振祥. 钢筋混凝土非线性分析[M]. 上海: 同济大学出版社, 1984: 50-240.
ZHU Bolong, DONG Zhenxiang. Nonlinear analysis of reinforced concrete[M]. Shanghai: Tongji University Press, 1984: 50-240.
[4] 彭向和, 杨春和. 复杂加载史下混凝土的损伤及其描述[J]. 岩石力学与工程学报, 2000, 19(2): 157-164.
PENG Xianghe, YANG Chunhe. The damage and its description of concrete under complex loading history[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(2): 157-164.
[5] 陈升平, 蒋俊玲, 李四年. 混凝土拉伸损伤演变的细观力学研究[J]. 工程力学, 2003, 20(5): 190-193.
CHEN Shengping, JIANG Junling, LI Sinian. Micromechanical analysis of damage evolution of concrete under tension[J]. Engineering Mechanics, 2003, 20(5): 190-193.
[6] 沈聚敏, 王传志. 钢筋混凝土有限元与板壳极限分析[M]. 北京: 清华大学出版社, 1993: 1-50.
SHEN Jumin, WANG Chuanzhi. Finite element and plates & shells analysis of reinforced concrete[M]. Beijing: Tsinghua University Press, 1993: 1-50.
[7] GB/T 50082—2009, 普通混凝土长期性能和耐久性能试验方法[S].
GB/T 50082—2009, Standard for test method of long-term performance and durability of ordinary concrete[S].
[8] 商怀帅. 引气混凝土冻融循环后多轴强度的试验研究[D]. 大连: 大连理工大学土木水利学院, 2006: 16-17.
SHANG Huaishuai. Experimental study on strength of air-entrained concrete under multiaxial loads after freeze-thaw cycles[D]. Dalian: Dalian University of Technology. School of Civil & Hydraulic Engineering, 2006: 16-17.
[9] 商怀帅, 宋玉普, 覃丽坤. 普通混凝土冻融循环后性能的试验研究[J]. 混凝土与水泥制品, 2005, 18(2): 9-11.
SHANG Huaishuai, SONG Yupu, QIN Likun. Experimental study on properties of concrete after freezing and thawing cycles[J]. China Concrete and Cement Products, 2005, 18(2): 9-11.
[10] Kachanov L M. Time of the rapture process under creep conditions[J]. TVZ Akad Nauk S S R Otd Tech Nuak, 1958, 8: 26-31.
[11] Lemaitre J. Application of damage concepts to predict creep- fatigue failure[J]. J Eng Mat Tech, ASME, 1979, 101(1): 202-209.
[12] 余天庆, 钱济成. 损伤理论及其应用[M]. 北京: 国防工业出版社, 1993: 35-66.
YU Tianqing, QIAN Jicheng. Damage theory and its application[M]. Beijing: National Defence Industry Press, 1993: 35-66.
[13] Dougill J W, Lau J C, Burt N J. Mechanical in engineering[M]. ASCE-END, 1976: 335-355.
[14] 王春来, 徐必根, 李庶林, 等. 单轴受压状态下钢纤维混凝土损伤本构模型研究[J]. 岩土力学, 2006, 27(1): 151-154.
WANG Chunlai, XU Bigen, LI Shulin, et al. Study on a constitutive model of damage of SFRC under uniaxial compression[J]. Rock and Soil Mechanics, 2006, 27(1): 151-154.
[15] 覃丽坤. 高温及冻融循环后混凝土多轴强度和变形试验研究[D]. 大连: 大连理工大学土木水利学院, 2003: 74-76.
QIN Likun. Study on the strength and deformation of concrete under multiaxial stress after high-temperature or freeze-thaw cycling[D]. Dalian: Dalian University of Technology. School of Civil & Hydraulic Engineering, 2003: 74-76.
(编辑 陈灿华)
收稿日期:2011-12-25;修回日期:2012-03-12
基金项目:国家自然科学基金资助项目(51208273);山东省高等学校科技计划项目(J12LG07);大连理工大学工业装备结构分析国家重点实验室研究基金资助项目(GZ1206)
通信作者:商怀帅(1980-),男,山东潍坊人,副教授,从事结构工程研究;电话:15092260928;E-mail: shanghuaishuai@163.com