J. Cent. South Univ. Technol. (2011) 18: 633-641

DOI: 10.1007/s11771-011-0741-3

Application of extension neural network to safety status pattern recognition of coal mines

ZHOU Yu(周玉)^{1, 2, 3}, W. Pedrycz^{3, 4}, QIAN Xu(钱旭)¹

1. School of Mechanical Electronic and Information Engineering,

China University of Mining and Technology (Beijing), Beijing 100083, China;

2. North China Institute of Water Conservancy and Hydroelectric Power, Zhengzhou 450011, China;

3. Department of Electrical and Computer Engineering, University of Alberta, Edmonton, T6G 2G7, Canada;

4. Systems Research Institute, Polish Academy of Sciences, 01-447 Warsaw, Poland

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: In order to accurately and quickly identify the safety status pattern of coal mines, a new safety status pattern recognition method based on the extension neural network (ENN) was proposed, and the design of structure of network, the rationale of recognition algorithm and the performance of proposed method were discussed in detail. The safety status pattern recognition problem of coal mines can be regard as a classification problem whose features are defined in a range, so using the ENN is most appropriate for this problem. The ENN-based recognition method can use a novel extension distance to measure the similarity between the object to be recognized and the class centers. To demonstrate the effectiveness of the proposed method, a real-world application on the geological safety status pattern recognition of coal mines was tested. Comparative experiments with existing method and other traditional ANN-based methods were conducted. The experimental results show that the proposed ENN-based recognition method can identify the safety status pattern of coal mines accurately with shorter learning time and simpler structure. The experimental results also confirm that the proposed method has a better performance in recognition accuracy, generalization ability and fault-tolerant ability, which are very useful in recognizing the safety status pattern in the process of coal production.

Key words: safety status; pattern recognition; extension neural network; coal mines

1 Introduction

The coal mining is one of the most important industries in the world. However, historically, the coal mining has been a very dangerous activity. Thousands of miners die from mining accidents each year, especially in the process of coal production. So, the safety of coal mines is always a primary concern in the coal mining business especially for the underground coal mining.

The safety accidents of coal mines occur mainly because the production system of coal mines is a complicated system. The operation underground is the basic feature of coal mines production system. Compared with other production systems on the ground, the system of coal mines has unsafe and natural hazards, i.e., geological condition, coal gas, coal dust, coal self-ignition and underground water hazard [1]. So, the safety status pattern recognition and safety evaluation system of coal mines plays a very important role in coal mines safety and it is one of the fundamental factors for the safe production of coal mines. Therefore, it is of great importance to accurately identify and recognize the safety status pattern of coal mines as early as possible, so that potential risks to personnel may be predicted, relevant measures can be taken to prevent accidents and the safe working condition can be created with the minimum investment. Hence, the research on techniques and methods of safety status pattern recognition and evaluation in coal mines have become a hot research area in the world. The latest techniques on the analytic hierarchy process (AHP) methods [2-3], fuzzy comprehensive evaluation methods [4-5], artificial neural network (ANN) methods [6-7], extension theory- based methods [8-9] etc have extensive applications in safety status recognition and evaluation. Nevertheless, it is more or less restricted and disadvantageous in previous methods. For example, the AHP-based methods and the fuzzy comprehensive evaluation methods require human expertise to determine the weights of each index and the fuzzy rules, respectively, so these methods cannot avoid the influence from human factor. Moreover, there are some difficulties in acquiring knowledge and in maintaining the database. The traditional ANN-based methods can directly acquire experience from the training data, and overcome some of the shortcomings of subjectivity. However, certain issues, such as local convergence and determination of the structure of network are not easy to handle, and some control parameters must be resolved before the ANNs become a practical tool. Furthermore, the training data must be sufficient and high-quality to ensure proper training. Compared with other traditional AI methods, the extension-theory-  based methods do not require particular artificial parameters. In addition, the use of dependent function can make the recognition and evaluation quantitative and qualitative, and the comprehensive dependent degree is taken as the recognition and evaluation criterion so as to avoid the subjectivity caused by human during the recognition and evaluation. But, it is sometimes very difficult to build dependent functions, which need very strong professional engineering background. Furthermore, the extension-theory-based methods have no learning and adaptive ability for significant and new information.

The objective of this study is to bring forward a novel safety status pattern recognition method based on the extension neural network (ENN) [10] for coal mines, which can overcome shortcomings and limitations existing in the current methods. The ENN is a relatively new neural network and invented by WANG [10-11]. The ENN permits recognition and classification of problems whose features are defined over a range of values. This new neural network is a combination of the extension theory [12-13] and the ANN. The ENN uses a modified extension distance to measure the similarity between the objects and the class centers. It can quickly and stably learn to categorize input patterns and permit the adaptive processes to access significant new information. Moreover, the ENN has shorter learning time and a simpler structure than the traditional ANNs. There have been many applications of based-ENN in the field of pattern recognition, fault diagnosis, classification, cluster analysis and so on [14-18]. To demonstrate the effectiveness of the proposed method, a real-world application was tested. Comparative study of the existing BP-based method and the other ANN-based method were conducted.

2 Theoretical background

2.1 Summary of extension theory

Extension theory was established by CAI to solve contradictions and incompatibility problems in 1983 [12-13]. The hard cores of the extension theory are two theoretical pillars that include the matter-element theory and the theory of extension set. In the former, the matter- elements and their transformations are studied; it can be easy to represent the nature of the matter. The latter is the quantitative tool of extension theory; it can represent the dependent degree of two matter-elements in the designed dependent functions.

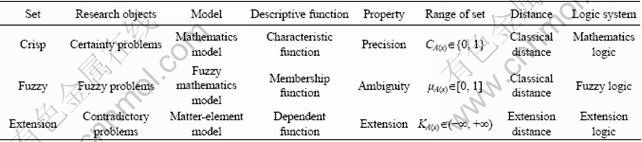
The extension set extends the crisp set and the fuzzy set. In the crisp set, an element either belongs to or does not belong to a set, so the range of the truth-values is {0, 1}, which can be used to solve a two-valued problem. In contrast to the crisp set, the fuzzy set allows for the description of concepts in which the boundary is not explicit. It concerns not only whether an element belongs to the set but also to what degree it belongs. The range of membership function is [0, 1] in fuzzy set. The extension set extends the fuzzy set from [0, 1] to (-∞, +∞). This means that an element belongs to any extension set to a different degree. The dependent function is defined to represent the degree to which an element belongs to a set. The comparisons of crisp set, fuzzy set and extension set are shown in Table 1.

Now, the extension theory has been used in the research field of artificial intelligence (AI) and its relevant sciences. The extension-theory-based methods have been applied to some engineering fields [8-9, 13, 19-22]. The detailed content about the extension theory can be referred to Refs.[12-13, 23].

2.2 Theory of extension neural network (ENN)

There are some recognition and classification problems whose features are defined in a range. For these problems, it is difficult to implement an appropriate classification method using the current neural networks. Therefore, a new topology of neural network (ENN) was proposed by WANG [10] to solve these problems.

Table 1 Comparisons among crisp set, fuzzy set and extension set

The schematic structure of ENN is depicted in Fig.1. It consists of both the input layer and the output layer. The neuron nodes in the input layer receive an input vector and, using a set of weighted parameters, generate an image of input data. There are two connection weights between the input neuron nodes and the output neuron nodes. One connection weight represents the up-bound for the classical domain of the feature and the other connection weight represents the low-bound for the required domain of the feature. The connection weights between the j-th input node and the k-th output node are  and  respectively. The output layer is a competitive layer. There is one node in the output layer for each prototype pattern, and only one output node with nonzero output to indicate the prototype pattern that is closest to the input vector.

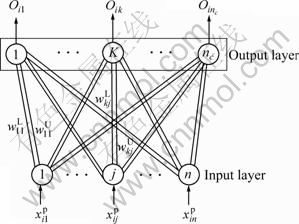
Fig.1 Schematic structure of extension neural network (ENN)

This new neural network involves the combination of the extension theory and the neural network. It uses the extension distance (as shown in Eq.(1)) to measure similarities between the tested data and the class centers:

                  (1)

The extension distance can be used to describe the distance between a point x and a range áw^L, w^U?. It can be presented in Fig.2.

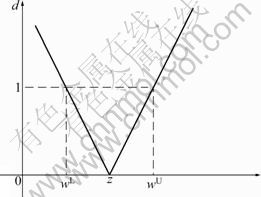
Fig.2 Extension distance

The learning of the ENN can be seen as supervised learning. The purpose of learning is to tune the weights of the ENN to achieve good classification performance or to minimize the classification error. The major steps of learning algorithm can be described as follows.

Let the training data set be  where N_p is the total number of training instances. The i-th instance in training data set is   where n is the total number of the feature of instances, and p denotes the category of the i-th instance. To evaluate the ENN performance, the error rate function E_T is defined as

                                  (2)

where N_m is the total error number.

First, set the initial connection weights according to the range of classical domains, and calculate the initial class center of each class. Then, input the training data set. Suppose the i-th (i=1, 2, …, N_p) training instance X_i and its corresponding label p are read. Use the extension distance to calculate the distance between the training instance  and the k-th class:

         (3)

where

Find k^*, such that  If k^*=p, then input the next training instance and calculate the extension distance; otherwise update the weights of the p-th and the k^*-th classes as Eq.(4)-(7). Repeat the above steps until the training process has converged, or the total error rate E_T has arrived at a preset value.

1) Update the centers of the p-th and the k^*-th clusters:

                                             (4)

                                            (5)

2) Update the weights of the p-th and the k^*-th classes:

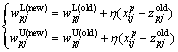                                 (6)

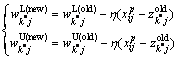                                 (7)

where η is a learning rate. The result of tuning the weights of two classes is shown in Fig.3 clearly, indicating the change of d_A and d_B. The category of instance x_ij is changed from class A to B due to d_A>d_B. From this step, it can be clearly seen that the learning process is only to adjust the weights of the p-th and the k^*-th class. Therefore, the proposed method has a speed advantage over the other supervised learning algorithms, and can quickly adapt to new and important information.

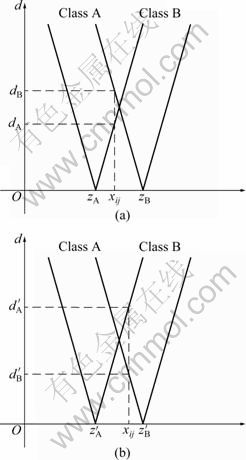
Fig.3 Results of tuning weights: (a) Original weights; (b) After tuning

3 ENN-based safety status pattern recognition method

3.1 Advantages of ENN-based recognition method

Generally, the historical database about the safety status of coal mines is very limited. The traditional ANN-based methods are not appropriate for application in this field due to needing a large amount of training data that are both correct and in high-quality. In contrast, the proposed ENN-based recognition method needs no special demands on training data and it is only to find the range of each feature. The range of each feature can be directly obtained from the previous experience, determined from limited training data, or obtained by means of data mining technique, which are convenient and easy relatively. Moreover, the problem of recognition and evaluation of the safety status of coal mines is a problem whose features are defined in a range. So, it is hard to implement an appropriate recognition method using the traditional neural networks. At the same time, the structure design of the traditional neural networks is sometimes not an easy problem, especially the determination of the number of neurons in the hidden layer and some control parameters. Furthermore, most of the traditional neural networks are based on complex algorithms, which increases the learning time and leads to an unefficient computing. Therefore, the ENN-based method is used to design the pattern recognition system for coal mines safety status. Compared with other methods, the ENN-based pattern recognition method has the following advantages:

1) It is not strict with the historical database. In the traditional ANN, the training data must be sufficient and compatible to ensure proper training.

2) The design of structure is simple. We just need to know the number of features of input pattern and the number of status patterns.

3) The initial weights of ENN are certain, which can be directly determined from the training data according to the upper bound and lower bound of input features.

4) The ENN is very appropriate for the recognition problem whose features are defined in a range.

5) The proposed method has a speed advantage because of the learning algorithm. The proposed method permits fast adaptive processes for the new data.

3.2 Structure design of ENN

The environment and working condition of underground coal mines are very complicated, which involve many hazards. All hazards constitute the dangerous sources to the operating workers and production system in the coal mines. Each hazard in coal mines includes many factors influencing the safety status of coal mines. Different kinds of hazard have different numbers of factors. These factors of each hazard are chosen as the features and the resulting feature vector can be denoted by C=[c₁, c₂, …, c_n]. Here, n stands for the number of the features. Each hazard of coal mines has several safety status patterns. According to the engineering practice, previous studies [1, 6] and the opinion of relevant experts, the coal mines safety status is classified into five status patterns, i.e., pattern I: very safe (N₁); pattern II: safe (N₂); pattern III: moderately safe (N₃); pattern IV: unsafe (N₄) and pattern V: very unsafe (N₅).

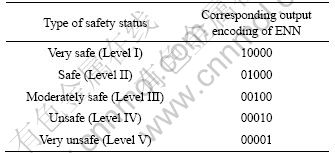
Compared with the traditional ANN, the problem of structure design of the ENN can be easier to solve. Based on the above discussion, the structure of the ENN consists of the input layer and the output layer. There are five output neuron nodes which correspond to five patterns of safety status of coal mines in the output layer, while there are n input neuron nodes which correspond to n features in the input layer. Only one output neuron node in the output layer remains active (the output value is 1) and the output values of other neuron nodes are zero to indicate a safety status pattern of the input instance. The safety status patterns of coal mines and the corresponding output encoding of the ENN are listed in Table 2.

Table 2 Types of safety status and corresponding output encoding of ENN

3.3 ENN-based recognition algorithm

The detailed ENN-based recognition algorithm can be described as follows.

Step 1: Prepare for the training data set.

Step 2: Set up the structure of the ENN.

Step 3: From the training data set, build the matter- models of each safety status pattern and set the connection weights between the input nodes and the output nodes by the matter-element models:

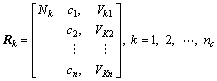                     (8)

In the extension theory, c_j is the j-th feature of N_k and  are the classical domains of the k-th class (N_k) about the j-th feature c_j. The range of classical domains can be directly obtained from the previous requirement, or determined from the training data:

                                (9)

                              (10)

Step 4: Calculate the initial center of each safety status pattern:

                                               (11)

      (12)

Step 5: Read the i-th training instance and its label of safety status pattern p

                   (13)

Step 6: Calculate the extension distance between the training instance  and the k-th safety status pattern using Eq.(3).

Step 7: Find the k^*, such that  If k^*=p then go to Step 9; otherwise Step 8.

Step 8: Update the weights of the p-th and the k^*-th classes according to Eqs.(4)-(7).

Step 9: Repeat Step 5 to Step 8. If all the instances have been classified, then a learning epoch is finished.

Step 10: Stop, if the learning process has converged, or the total error rate E_T has arrived at a preset value; otherwise, return to Step 5.

Step 11: Save the weight vector of the trained ENN;

Step 12: Use the trained ENN to recognize the safety status pattern of coal mines. Use the extension distance to measure the similarity between the tested object and each safety status pattern. Find the k^*, such that  and set  to indicate that the safety status pattern of the tested object is k^*.

Step 13: Stop, if all the tested objects have been recognized; otherwise go to Step 12.

The above algorithm can be represented with the flow chart, as shown in Fig.4.

4 Experimental results and discussion

A real-world example was taken as an example to illustrate the points of the ENN-based recognition method. The background of the example was the geological safety status pattern recognition in coal mines. According to the degree of influence of the various factors upon the geological safety status of coal mines and in agreement with past studies [6, 9], the following four main factors were chosen as the features for the recognition of the geological safety condition of coal mines. These features of input patterns would be most useful for recognition. These features included the average fault throw c₁, the fault number per unit area c₂, the variation coefficients of coal seam thickness c₃ and the difficulty degree of management of roof and floor c₄. So, the feature vector of the geological safety status of coal mines could be denoted by C=[c₁, c₂, c₃, c₄]. Based on section 3.2, the structure of ENN for the application of geological safety status recognition comprised both the input layer and the output layer. The numbers of the input neuron nodes and the output neuron nodes were 4 and 5, respectively. The historical data sets came from Ref.[6]. To prove the efficiency and validity of the proposed ENN-based recognition method, some experiments were given.

4.1 Experiment 1: Comparison with existing method

The purpose of this experiment was to compare with the BP-based method in Ref.[6], so the experiment environment was the same as Ref.[6]. The training data set contained 20 instances (as listed in Table 3) and the testing data set contained five instances (as listed in Table 4). According to the training data set, the element-models of each safety status pattern of coal mines geology were built (as listed in Table 5). The learning rate is an important parameter for ANN. With other ANN models, the greater the learning rate of ENN is, the shorter the time required for ENN learning is. Of course, when the learning rate is greater than a certain value, the processing of learning would oscillate, even diverge. According to the experience, the learning rate η was set to be 0.1 in the following experiments. Training data set was used to train ENN, and then the testing data set was used to test this recognition method. The simulation results are shown in Table 4, which indicates that this method can accurately distinguish the five testing instances.

Fig.4 Flow chart of recognition method based on ENN

Table 3 Training data sets of geological safety status of coal mines

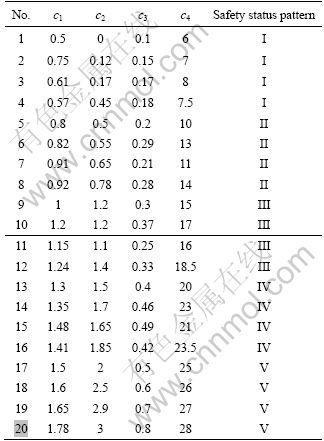
Table 4 Testing data sets and actual outputs of ENN

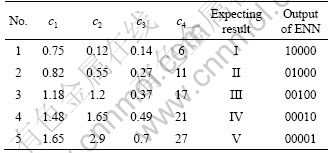
In order to test the generalization ability, the leave- one-out cross-validation (LOOCV) experiment was carried out. LOOCV involves using a single instance from the original data as the validation data, and the remaining instances as the training data. It is repeated such that each observation in the sample is used once as the validation data. In this experiment, 25 times training processes were repeated. At each time, one instance was used as the testing data and other 24 instances were used as the training set. For the ENN-based method, the total error number was 2, and the average error recognition rate is 8%. The same experiment was done using the BP-based recognition method and the average error recognition rate was 12%. It is obvious that the ENN-based recognition method has strong generalization ability.

Table 5 Matter-element models of geological safety status patterns of coal mines

In Table 6, the performance of the proposed method is compared with the existing BP-based method [6]. From Table 6, we can clearly find that the proposed ENN-based method has a shorter learning time than the BP-based method. The BP-based method needs 980 epochs before recognition. Contrarily, the ENN-based method only spends 1 epoch. As exhibited in Table 6, it should be noted that the structure of proposed ENN is simpler than the BP neural network. To be specific, the BP-based method is a four-layer structure, i.e. the input level, the first hidden layer, the second hidden layer and the output layer, and the numbers of neuron node of each layer are 4, 7, 5, and 1, respectively. The BP neural network needs 68 connection weights. In contrast, the proposed ENN-based recognition method is only a two-layer structure, that is, the input layer and the output layer, and the numbers of neuron nodes of each layer are 4 and 5, respectively. The number of connection weights is 40. Furthermore, the learning error of the proposed method can achieve zero. As well, the accurate rates are quite high with 100% and 92% for testing data sets and LOOCV. On the other hand, unlike the BP-based method, the proposed method can determine the initial weights from the training data set, while the initial weights of the BP-based method are uncertain.

4.2 Experiment 2: Comparison with other ANN-based methods

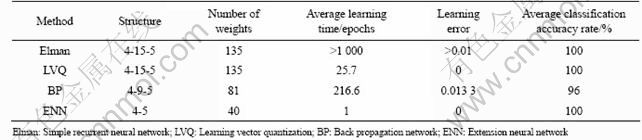
In this experiment, the training data set contained 25 training instances (i.e., the full data from Table 3 and Table 4) and the testing data set was equal to the training data set, containing 25 instances. Several ANN-based methods were used to compare the performance. To be more objective, each method was done 10 times and the average results were taken. In Table 7, the performance of the proposed ENN-based method is compared with the other recognition methods in the same data set (The BP-based method in this experiment is different from that in experiment 1 which is the same as Ref.[6]. The performance of the BP-method in this experiment is better). It can be seen from Table 7 that the proposed ENN-based method is at least as good as the other methods in recognition accuracy and learning error, but it has a shortest learning time and a simplest structure. Moreover, the proposed ENN-based method can take expert experiences before learning, and can also produce meaningful output after learning, because the optimal classified boundary of the features is clearly determined. On the other hand, the proposed ENN-based method permits fast adaptive process for significant and new information, and it is easy to acquire the knowledge and maintain the classification database.

Table 6 Comparison results of BP-based method and ENN-based method

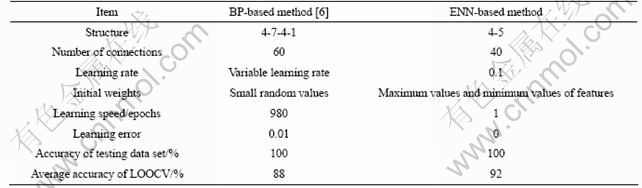
Table 7 Comparison of recognition performance of various methods

4.3 Experiment 3: Tests of error-containing data

The environment of coal mines is so complex and the parameters are changeable and uncertain, so the input data of the geological safety status pattern recognition system would unavoidably contain some noise and uncertainties. The sources of error include environmental noise, sensors, human mistakes, etc, which could lead to data uncertainties and errors. To take into account of the noise and uncertainties, all data (25 instances) were created by adding 0% to ±30% of random, uniformly distributed error to the training data to evaluate the fault-tolerant ability of the proposed ENN-based recognition method. The testing results using different amounts of errors added are given in Table 8 for the different recognition methods. Usually, the error containing data indeed degrade the recognition capabilities in proportion to the amounts of error added. Table 8 shows that ENN-based method can bear remarkable tolerance to the errors contained in the data. It should be noted that the proposed ENN-based recognition method has a significantly higher recognition accuracy of 100% with ±30% errors added, and Fig.5 shows one of learning curves with ±30% errors added. From Table 8, we can find that the Elman-based method and the BP-based method also have a good fault-tolerant ability, but both methods need much time to train the network in the actual application. For the LVQ-based method, the fault-tolerant ability is not very good. Under the same conditions, the average accuracy rate is less than 50% with ±30% errors added. This experiment proves that the ENN-based recognition method has the best fault-tolerant ability.

Table 8 Recognition performances of different methods with different percentages of noise added

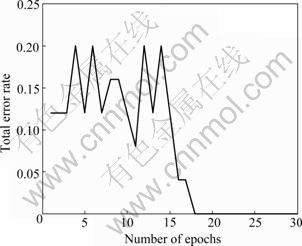
Fig.5 Learning curves with ±30% errors added

5 Conclusions

1) A novel recognition method based on the ENN for the safety status of coal mines is proposed. The structure design of network and the recognition algorithm are presented in detail. Compared with the other traditional ANN-based methods, the design of the ENN structure and the learning algorithm is simple.

2) The results of experiments indicate that, compared with the results of other ANN-based methods, the ENN-based recognition method has the advantage of less learning time, lower learning error and higher accuracy. Moreover, the proposed recognition method has strong generalization ability and excellent fault tolerant ability, which are the most important aspects for overall evaluation of the safety status pattern recognition system of core mines.

3) The tested results indicate that this method is more efficient in engineering applications of safety of coal mines.

References

[1] SHI Shi-liang, LI Run-qiu, XIE Jian-xiang. Theoretical study on safety assessment indexes system of coal mines [J]. Journal of Coal Science and Engineering, 2003, 9(2): 63-69.

[2] LIU Ya-jing, MAO Shan-jun, LI Mei, YAO Ji-ming. Study of a comprehensive assessment method for coal mine safety based on a hierarchical grey analysis [J]. Journal of China University of Mining & Technology, 2007, 17(1): 6-10.

[3] WANG Bing-qiang, SHEN Zhi-hui, BAI Xi-qing. Application of AHP in mine environmental geological evaluation [J]. Coal Geology of China, 2007, 19(10): 57-59. (in Chinese)

[4] WU Li-ping, WU Shi-yue, GUO Yong-yi. Study on fuzzy mathematics to mine safety comprehensive assessment [J]. Journal of Taiyuan University of Technology, 2006, 37(2): 131-133. (in Chinese)

[5] YAO Wei. The comprehensive assessment of geological environment and disasters prevention cure in Shenfu Dongsheng mining area [D]. Xi’an: Xi’an University of Science and Technology, 2002. (in Chinese)

[6] SHI Shi-liang, WANG Hai-qiao. Non-linear dynamic safety assessment in coal mines [M]. Beijing: Coal Industry Press, 2001. (in Chinese)

[7] SUN Gang, ZHANG Rui-xin, LUO Fen. Evaluation method of coal mine production safety based on BP neural network [C]// Proceedings of the 2009 International Conference on Information Technology and Computer Science-Volume 01. Washington: IEEE Computer Society, 2009: 514-517.

[8] ZHOU Yu, QIAN Xu, JIAN Tao. Research on the extension assessment model of underground coalmine safety behavior [J]. Journal of China University of Mining & Technology, 2009, 38(4): 515-522. (in Chinese)

[9] ZHOU Yu, QIAN Xu, ZHAO Jin-hui. Application of extension theory to the evaluation of coal mines geological safety [C]// Proceedings of the 21st Annual International Conference on Chinese Control and Decision Conference. Piscataway: IEEE Press, 2009: 4937-4941.

[10] WANG M H, HUNG C P. Extension neural network and its applications [J]. Neural Networks, 2003, 16(5): 779-784.

[11] ZHOU Yu, QIAN Xu, ZHANG Jun-cai. Survey and research of extension neural network [J]. Application Research of Computers, 2010, 27(1): 1-5. (in Chinese)

[12] CAI Wen. The extension set and incompatibility problem [J]. Journal of Scientific Exploration, 1983, 1: 81-93.

[13] CAI Wen. Extension theory and its application [J]. Chinese Science Bulletin, 1999, 44(17): 1538-1548.

[14] MOHAMED S, TETTEY T, MARWALA T. An extension neural network and genetic algorithm for bearing fault classification [C]// IJCNN '06. International Joint Conference on Neural Networks, Vancouver: 2006: 3941-3948.

[15] WANG M H. Extension neural network-type 2 and its applications [J]. IEEE Trans on Neural Networks, 2005, 16(6): 1352-1361.

[16] WANG M H. Partial discharge pattern recognition of current transformers using an ENN [J]. IEEE Tarns on Power Delivery, 2005, 20(3): 1984-1990.

[17] VILAKAZI C B, MARWALA T. Bushing fault detection and diagnosis using extension neural network [C]// Proceedings of the 10th IEEE International Conference on Intelligent Engineering Systems. London: 2006: 170-174.

[18] CHAO K H, WANG M H, HSH C C. A novel residual capacity estimation method based on extension neural network for lead-acid batteries [J]. Lecture Notes in Computer Science, 2007, 4493: 1145-1154.

[19] WANG M H, TSENG Y F. A novel clustering algorithm based on the extension theory and genetic algorithm [J]. Expert Systems with Applications, 2009, 36(4): 8269-8276.

[20] DENG Hong-gui, CAO Jian, LUO An. Application of extension method to fault diagnosis of transformer [J]. Journal of Central South University of Technology, 2007, 14(1): 88-93.

[21] WANG M H. Application of extension theory to PD pattern recognition in high-voltage current transformers [J]. IEEE Trans on Power Delivery, 2005, 20(3): 1939-1946.

[22] JUN Ye. Application of extension theory in misfire fault diagnosis of gasoline engines [J]. Expert Systems with Applications, 36(2): 1217-1221

[23] CAI Wen, YANG Chun-yan. Extension engineering methods [M]. Beijing: Science Press, 2003.

(Edited by YANG Bing)

Foundation item: Project(107021) supported by the Key Foundation of Chinese Ministry of Education; Project(2009643013) supported by China Scholarship Fund

Received date: 2009-11-04; Accepted date: 2010-05-10

Corresponding author: ZHOU Yu, PhD Candidate; Tel: +86-15037128252; E-mail: zhouyu_beijing@126.com