Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions
来源期刊:中南大学学报(英文版)2019年第5期
论文作者:Hamid MALEKI Jalal ALSARRAF Abbas MOGHANIZADEH Hassan HAJABDOLLAHI Mohammad Reza SAFAEI
文章页码:1099 - 1115
Key words:radiation; slip condition; porous surface; heat generation/absorption; viscous dissipation; nanofluid
Abstract: Presence of different terms with various values can alter the thermal behavior of the nanofluids flow over porous surfaces. The aim of this research is to study the influence of nanoparticles volume fraction, nanoparticles type, suction or injection, the heat generation or absorption, the Eckert number, thermal and velocity slip parameters, and radiation on the velocity and temperature fields on the flow and heat transfer over a porous flat plate. Four different types of nanoparticles including metal nanoparticles (Cu), metal oxide nanoparticles (Al2O3) and carbon-based nanomaterials (MWCNTs and SWCNTs) which were dispersed in the water (as based fluid) are studied. The governing equations are converted into the ordinary differential equations using similarity solution and solved numerically by the RKF45 algorithm. The results of the simulations showed a contradiction with the results of other researchers who expressed that using nanoparticles with higher thermal conductivity and volume fraction led to increasing heat transfer rate in nanofluids; this study proves that, in some cases, boosting the volume fraction of nanoparticles has a potential to decrease the heat transfer rate due to significant changes in values of some parameters including radiation, heat generation, and viscous dissipation.
Cite this article as: Hamid MALEKI, Jalal ALSARRAF, Abbas MOGHANIZADEH, Hassan HAJABDOLLAHI, Mohammad Reza SAFAEI. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions [J]. Journal of Central South University, 2019, 26(5): 1099–1115. DOI: https://doi.org/10.1007/ s11771-019-4074-y.

ARTICLE
J. Cent. South Univ. (2019) 26: 1099-1115
DOI: https://doi.org/10.1007/s11771-019-4074-y
Hamid MALEKI1, Jalal ALSARRAF2, Abbas MOGHANIZADEH3,Hassan HAJABDOLLAHI4, Mohammad Reza SAFAEI5, 6
1. Department of Mechanical Engineering, Isfahan University of Technology, Isfahan 84156-83111, Iran;
2. Department of Automotive and Marine Engineering Technology, College of Technological Studies, The Public Authority for Applied Education and Training, Kuwait;
3. Biomaterial Research Group, Department of Materials Engineering, Isfahan University of Technology, Isfahan 84156-83111, Iran;
4. Department of Mechanical Engineering, Vali-e-Asr University of Rafsanjan, Rafsanjan, Iran;
5. Division of Computational Physics, Institute for Computational Science, Ton Duc Thang University,Ho Chi Minh City, Vietnam;
6. Faculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Vietnam
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Presence of different terms with various values can alter the thermal behavior of the nanofluids flow over porous surfaces. The aim of this research is to study the influence of nanoparticles volume fraction, nanoparticles type, suction or injection, the heat generation or absorption, the Eckert number, thermal and velocity slip parameters, and radiation on the velocity and temperature fields on the flow and heat transfer over a porous flat plate. Four different types of nanoparticles including metal nanoparticles (Cu), metal oxide nanoparticles (Al2O3) and carbon-based nanomaterials (MWCNTs and SWCNTs) which were dispersed in the water (as based fluid) are studied. The governing equations are converted into the ordinary differential equations using similarity solution and solved numerically by the RKF45 algorithm. The results of the simulations showed a contradiction with the results of other researchers who expressed that using nanoparticles with higher thermal conductivity and volume fraction led to increasing heat transfer rate in nanofluids; this study proves that, in some cases, boosting the volume fraction of nanoparticles has a potential to decrease the heat transfer rate due to significant changes in values of some parameters including radiation, heat generation, and viscous dissipation.
Key words: radiation; slip condition; porous surface; heat generation/absorption; viscous dissipation; nanofluid
Cite this article as: Hamid MALEKI, Jalal ALSARRAF, Abbas MOGHANIZADEH, Hassan HAJABDOLLAHI, Mohammad Reza SAFAEI. Heat transfer and nanofluid flow over a porous plate with radiation and slip boundary conditions [J]. Journal of Central South University, 2019, 26(5): 1099–1115. DOI: https://doi.org/10.1007/ s11771-019-4074-y.
1 Introduction
Many researches pay more attention to flow and thermal behaviors of permeable plates since studying this issue is valuable in a wide variety of engineering applications from airfoil boundary layer control to lubrication and cooling of bearings, nuclear reactors, turbine blades, electronics and many other industrial systems [1].
Two significant characterizations of permeable surfaces are suction and injection that has strong influence on the heat transfer and fluid flow on the surface. Generally, suction causes increasing heat transfer and skin-friction coefficients; while injection shows an opposite impact [1]. In this regard, ISHAK [2] presented similarity solution for the heat transfer over a permeable flat plate with convective boundary condition. He proved that similarity solution for steady, laminar boundary layer flow over a permeable surface exist when the permeability parameter and the convection heat transfer from the hot fluid change with a proportion of x-1/2, where x is the distance from the leading edge of the surface. ISAIAH et al [3] tested the transient flow and heat transfer over a permeable plate numerically. This study was conducted in the presence of a strong magnetic field with convective boundary condition. They examined the effects of various parameters such as Hall currents, suction velocity, magnetic interaction, Grashof number and time on the thermofluid characteristics. RITA et al [4] developed a mathematical model to study the influence of a viscoelastic fluid on magnetohydrodynamic (MHD) boundary layer flow over a permeable surface. They solved the governing equations using a semi-analytical method (perturbation technique). Their method can be utilized to solve a broad range of industrial applications and chemical processes. SADRI et al [5] investigated the flow and heat transfer on a permeable flat plate with constant wall temperature. They converted the governing PDEs into ODEs by means of befitting transformations, and then solved the resulting equations with analytical (optimal homotopy asymptotic) and numerical methods. They studied the impacts of suction and injection on the temperature and velocity profiles. YASIN et al [6] studied numerically the MHD flow and heat transfer over a stretching/shrinking permeable plate considering the effect of radiation. They investigated the impacts of various parameters such as permeability, stretching/shrinking, radiation, magnetic, heat absorption/generation, and chemical rate parameter on the local Nusselt number, skin friction factor, and local Sherwood number. RAJU et al [7] numerically investigated the influence of thermal radiation, heat absorption, suction and chemical reaction on unsteady MHD fluid flow and heat transfer over a semi-infinite vertical moving permeable surface. SINGH et al [8] studied the mixed convection slip flow over a continuously moving vertical surface. They examined the impacts of moving plate parameter, the slip velocity, buoyancy force and convective heating on velocity and temperature profiles. EEGUNJOBI et al [9] studied the influence of buoyancy, radiation, chemical reaction, slip velocity and magnetic field on unsteady mixed convection heat transfer of working fluid over a stretching surface embedded in a porous medium. In another work, MUHAMMAD et al [10] examined numerically thermodynamics analysis of unsteady MHD flow over a vertical permeable plate. They considered the impacts of radiation, velocity and temperature slip, buoyancy force, viscous dissipation, Joule heating, and magnetic field.
Many researchers examined the flow and heat transfer over permeable surfaces in different cases. However, they utilized the regular fluid as the working fluid. That’s while, using of nanofluid as carrying fluid may cause different behaviors in fluid flow and heat transfer of the system.
Need to increase the efficiency and improve heat transfer in thermal systems led to extensive researches on utilizing of nanofluids instead of regular fluids. Adding a low amount of nanomaterials, such as metal nanoparticles [11–15], metal oxide nanoparticles [16–19] or carbon based materials [20–23] to base fluids, causes new thermophysical properties that can greatly affect the heat and mass transfer specifications of thermal systems [24, 25]. In recent years, the nanofluids have been utilized extensively in various applications such as electronic cooling [26–28], heat exchangers [29], renewable energy systems [30] in addition to the above mentioned fields, using nanofluids over flat plates can make significant changes in the specifications of flow and heat transfer in different applications. In this regard, HAJMOHAMMADI et al [1] studied numerically the fluid flow and heat transfer of Cu/ H2O and Ag/ H2O nanofluids over a permeable flat plate. Their results indicated that for impermeable plate and injection case, augmentation of nanoparticles volume fraction enhances the surface heat transfer rate. DAS et al [31] examined the effects of slip conditions on heat and mass transfer characteristics of MHD nanofluid flow over a non-linear stretching permeable plate. Their findings confirmed that in the presence of hydrodynamic and thermal slip conditions, increasing the suction and injection parameters have a considerable influence on the surface temperature of the plate. So that, by boosting the suction parameter, the surface temperature of the plate is diminished by more than 50%. However, with the increment of the blowing parameter, the surface temperature is increased by about 35%. ZIAEI-RAD et al [32] investigated numerically the mixed convection heat transfer of nanofluid flow over an inclined porous plate. Based on their results, increasing the suction parameter enhances the surface heat transfer rate. Also, they observed that by increasing the plate angle from 0° to 60°, the friction coefficient and Nusselt number increase by 240% and 25%, respectively. MOHAMMADIEN et al [33] carried out a numerical modeling to study the influence of magnetic and radiation parameters on CuO–H2O nanofluid flow over a permeable stretching plate. Their results demonstrated that the fluid velocity drops with rising permeability and magnetic parameters. Also, the fluid temperature rises with increasing the radiation and reducing the suction/injection parameters. The effect of carbon nanotube-based working fluid on heat transfer over a flat surface was examined by NANDEPPANAVAR et al [34]. They found that single-wall carbon nanotubes (SWCNTs) have better thermal performance, compared to multi-wall carbon nanotubes (MWCNTs). ETWIRE et al [35] reported the influence of viscosity and thermal conductivity on oil-based nanofluid flow over a vertical permeable plate. They showed that both skin friction factor and Nusselt number are enhanced by adding CuO nanoparticles into the working fluid. NAYAK [36] performed a semi-analytical analysis (Homotopy method) to study the 3-D MHD nanofluid flow and heat transfer over a shrinking plate. They considered the impacts of radiation as well as viscous dissipation. Their results depicted that radiation and viscous dissipation diminish the surface heat transfer rate. HAYAT et al [37] obtained convergent series solutions for Marangoni convection heat transfer and nanofluid flow. They confirmed that the Nusselt number shows substantial variations for the greater nanoparticles volume fraction and radiation parameters. MAKINDE [38] investigated numerically the combined impacts of Newtonian heating and viscous dissipation on heat transfer and fluid flow over a flat plate for different water based nanofluids including Cu, TiO2 and Al2O3. He observed that the Nusselt number enhances with rising nanoparticles volume fraction and Biot number. ZAIB et al [39] performed a numerical analysis to study the unsteady nanofluid flow and heat transfer over an exponentially shrinking permeable surface. Their results illustrated that for different nanoparticles volume fractions, the dual solutions exist only when a particular mass suction is applied.
Many researchers have studied the fluid flow and heat transfer on different types of stretching/ shrinking sheets [40–47]. It has been less attention to the conventional permeable flat plates. The most important studies on the flat permeable plates are of researches ISHAK [2] and HAJMOHAMMADI et al [1]. In fact, the present work can be considered the continuation of the studies of ISHAK [2] and HAJMOHAMMADI et al [1]. In the following two previous works, the authors discussed the different cases of a flat permeable plate, under the influence of various parameters. In fact, due to extensive use of permeable plates in various industries, different parameters such as thermal radiation, slip condition, viscous dissipation and heat generation/absorption can have different degrees of importance to affect the heat and mass transfer characteristics. Therefore, investigation of the combined influence of different parameters in the presence of various nanomaterials (metal, metal oxide and carbon-based nanoparticles) may cause complicated thermal behaviors and this point is the significant distinction between the present work and previous studies. In this regard, the governing PDEs are first converted into the ODEs utilizing similarity solution. Afterwards, obtained ODEs are solved numerically by Maple software [48]. Four different types of nanomaterials including metal nanoparticles (Cu), metal oxide nanoparticles (Al2O3) and carbon-based nanomaterials (SWCNTs and MWCNTs) are studied, using water as a base fluid.In the present investigation, combined effects of nanoparticles volume fraction, nanoparticles type, viscous dissipation, heat generation or absorption, radiation and slip boundary conditions on velocity and temperature fields of different modes of a porous plate (suction, injection and impermeable plate) are studied. Besides, all the aforementioned conditions are compared with base fluid that will be helpful to estimate the significant role of nanoparticles.
2 Mathematical formulation
The present investigation was performed by considering some assumptions including two- dimensional steady state condition, incompressible laminar flow, and slip flow boundary layer over a permeable plate. Thermo-physical properties of the water and nanomaterials are provided in Table 1 [49, 50]. Metal and metal-oxide nanoparticles are considered with uniform spherical shape and equal size. However, CNT nanomaterials are tube shape. Moreover, it is considered that the water and the nanomaterials are in thermal equilibrium and there is no slip between them [51, 52]. The flow model and its coordinate system are shown in Figure 1.
Table 1 Thermophysical properties of base fluid and nanomaterials [49, 50]
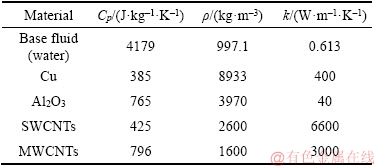

Figure 1 Coordinate system and flow model
Heat generation or absorption in some engineering application such as dissociating process has very significant effects. Volumetric rate of heat generation/absorption can be calculated as below (see Refs. [53, 54]):
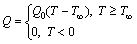 (1)
(1)
where Q0 is the heat generation/absorption coefficient.
The governing equations for boundary layer flow and heat transfer of nanofluids, with considering viscous dissipation, thermal radiation and heat generation/absorption are written as [55]:
 (2)
(2)
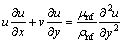 (3)
(3)

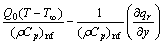 (4)
(4)
The proper boundary conditions including thermal and velocity partial slip are given by:
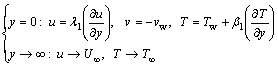 (5)
(5)
where u and v are the velocity components in the direction along and normal to the plate, respectively; U∞ indicates the free stream velocity; T represents the nanofluid temperature in the boundary layer; T∞ is assigned as the temperature of the fluid far from the plate; Tw is the temperature of the plate; λ1 is velocity slip parameter; β1 is thermal slip parameter, and vw is the mass velocity normal to the wall.
(ρCp)nf is the heat capacity of the nanofluid; μnf and ρnf are the dynamic viscosity and density of the nanofluid, respectively and αnf is the thermal diffusivity of the nanofluid. Thermophysical properties of nanofluid can be formulated as a combination of solid particles and base fluid properties, as follows:
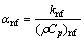 (6)
(6)
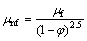 (7)
(7)
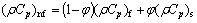 (8)
(8)
 (9)
(9)
where φ is the nanoparticles volume fraction; ρf and ρs are the densities of the base-fluid and solid particles, respectively. Viscosity of the nanofluid (μnf) is calculated based on BRINKMAN’s [56] recommendation. In order to calculate thermal conductivity of nanofluid (knf) for uniformly sized spherical Cu and Al2O3 nanoparticles, well-known Maxwell model [57] is used as follows:
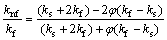 (10)
(10)
where kf and ks are the thermal conductivities of the base fluid and nanoparticles, respectively.
Various empirical correlations have been suggested to forecast the thermal conductivity of carbon nanotubes suspensions [58]. One of the most important studies in this field has been performed by XUE [59]. His findings showed that most of the existing correlations for nanofluids thermal conductivity are proper only for spherical or rotational elliptical particles. In addition, these formulas do not consider the impacts of the spatial distribution of carbon nanotubes on effective thermal conductivity. Therefore, XUE [59] presented a new model according to the Maxwell theory that accurately predicts the thermal conductivity of nanofluids including carbon nanotubes:
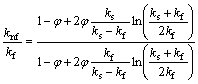 (11)
(11)
XUE’s model has been used in numerous studies related to carbon nanotube-based composites [60–63].
By utilizing the Roseland model [64–66], the radiative heat flux is estimated as:
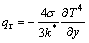 (12)
(12)
where k* is the mean absorption factor and σ is the Stefan–Boltzmann coefficient. Considering that the temperature differences inside the flow over the plate are enough small, T4 can be represented as a function of fluid temperature (T), applying a truncated Taylor series, concerning the ambient temperature (T∞), i.e.
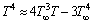 (13)
(13)
In order to transform PDEs into ODEs, the following dimensionless variables are proposed:
 (14)
(14)
where η, f, θ and ψ are the similarity variable, dimensionless stream function, dimensionless temperature and stream function, respectively. Continuity equation (Eq. (2)) is satisfied by stream function. This function is described as:
 (15)
(15)
Using the dimensionless variables (14), PDEs Eqs. (3) and (4) are reduced to the following ODEs:
 (16)
(16)

 (17)
(17)
Subjected to the boundary conditions Eq. (5), it becomes:
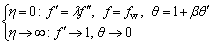 (18)
(18)
In the aforementioned equations, primes indicate differentiation with respect to η. γ is the local heat generation (>0) or absorption parameter (<0); fw is the local suction (>0) or the local injection parameter (<0); λ is the velocity slip parameter; β is the thermal slip parameter; N is the radiation parameter and Ec is the local Eckert number. In addition, m0, m1, m2, m3 are constant. Accordingly, following parameters are involved in the problem:
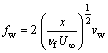 (19)
(19)
 (20)
(20)
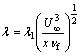 (21)
(21)
 (22)
(22)
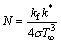 (23)
(23)
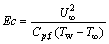 (24)
(24)
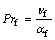 (25)
(25)
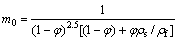 (26)
(26)
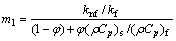 (27)
(27)
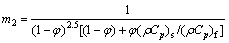 (28)
(28)
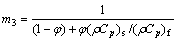 (29)
(29)
To obtain similarity solution for ODEs, all the parametersg, fw, l and b must be independent of x. These conditions are satisfied when heat generation/absorption coefficient (Q0) is in proportion to x–1, mass velocity normal to the wall (vw) is in proportion to x–1/2, and the velocity slip parameter (l1) and the thermal slip parameter (b1) are in proportion to x1/2. Therefore, it should be assumed that:
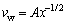 (30)
(30)
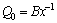 (31)
(31)
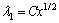 (32)
(32)
 (33)
(33)
where A, B, C and D are constants. Substituting Eqs. (30)–(33) into Eqs. (19)–(22), it can be concluded that:
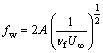 (34)
(34)
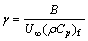 (35)
(35)
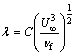 (36)
(36)
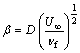 (37)
(37)
when fw, g, l and b are defined by Eqs. (34)–(37), the solutions of Eqs. (16)–(18) lead to the similarity solution.
The local skin-friction coefficient and local Nusselt number can be expressed as:
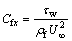 (38)
(38)
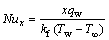 (39)
(39)
where the surface shear stress (τw) and the surface heat flux (qw) are given by:
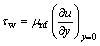 (40)
(40)
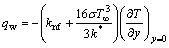 (41)
(41)
Using the dimensionless variables Eq. (14), it can be concluded that:
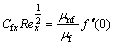 (42)
(42)
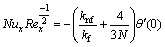 (43)
(43)
where Reynolds number is defined as follows:
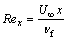
3 Numerical procedure and validation
The non-linear ODEs Eqs. (16) and (17), subject to the boundary conditions Eq. (18), are numerically solved utilizing the Runge–Kutta– Fehlberg fourth–fifth-order (RKF45) scheme, using Maple software. It is confirmed that the RKF45 algorithm in Maple has great accuracy [48]. The asymptotic far-field boundary conditions (Eq. (18)) at η→∞ are substituted by those at η=12, which is a standard procedure in boundary layer examinations [1, 2]. Also, the step size of the solution and the convergence criterion for the residuals were set to 0.05 and 10–6, respectively.
To ensure the precision of the present modeling, the distribution of dimensionless velocity and temperature are compared with those obtained by MOTSUMI et al [55]. As shown in Figure 2, the dimensionless velocity and temperature profiles for Al2O3/H2O and Cu/H2O nanofluids (j=0.1) and no-slip (b=l=0), fw=0.2, N=1, Ec=0.016 and g=0 conditions, reveal acceptable agreement with the former study of MOTSUMI et al [55].
4 Results and discussion
The effects of the nanomaterials type, volume fraction of nanoparticles, suction or injection, the heat generation or absorption, the Eckert number, radiation, thermal slip and velocity slip parameters on the flow and thermal fields are examined and explained in details in this section. In this study,three types of nanomaterials including metal type (Cu), metal oxide one (Al2O3) and carbon-based one (SWCNTs and MWCNTs) are evaluated, utilizing water as the working fluid. To simplify the results of considering various parameters, dimensionless velocity and temperature distribution diagrams have been reported only for MWCNTs nanomaterials (Figures 3–12). However, local skin friction factor and local Nusselt number for various nanoparticles are presented in Tables 2 and 3, respectively.
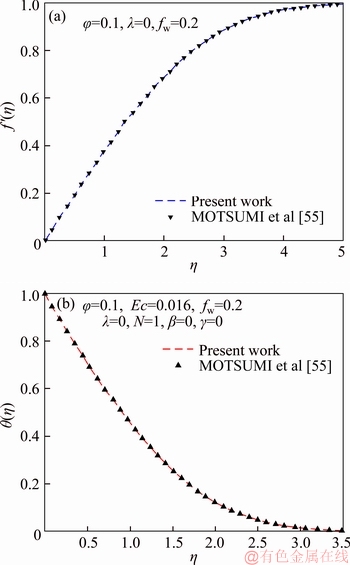
Figure 2 Comparison of present results with those of MOTSUMI et al [55] for velocity profiles (Al2O3 nanoparticles) (a) and temperature profiles (Cu nanoparticles) (b)
4.1 Influence of parameters variation on velocity profiles
The influence of nanoparticles volume fraction on the velocity profiles for different cases of the plate (suction, impermeable plate and injection) is exhibited in Figures 3(a)–(c). It is obvious that boosting the nanoparticles volume fraction causes a decrease in the velocity and extends the boundary layer thickness in the cases of suction and impermeable plate. However, the reverse results for the velocity variation trend are observed in the case of injection, especially near the surface. That’s while, in the research of HAJMOHAMMADI et al [1] the reverse of the above trend was observed for the suction and impermeable plate cases, in the presence of copper nanoparticles. This deviation shows that the thermophysical properties of nanoparticles can have a considerable impact on the flow behavior from the permeable plates. In addition, the effects of nanoparticles on the velocity profiles in the case of suction are found to be more effective, compared to two other cases.
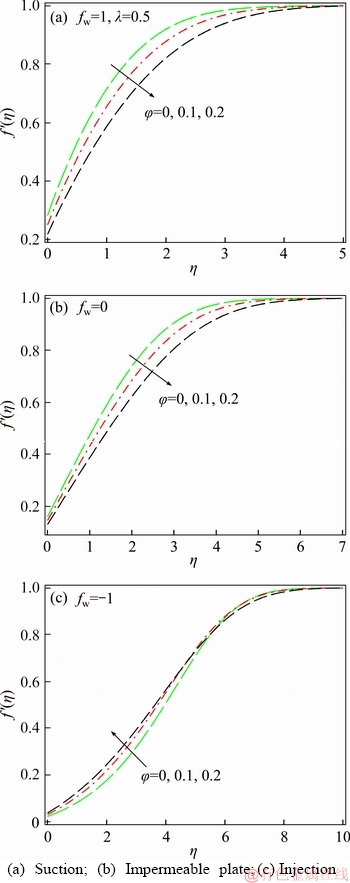
Figure 3 Velocity distribution for various nanoparticles volume fraction:

Figure 4 Velocity profiles for different values of permeability parameter
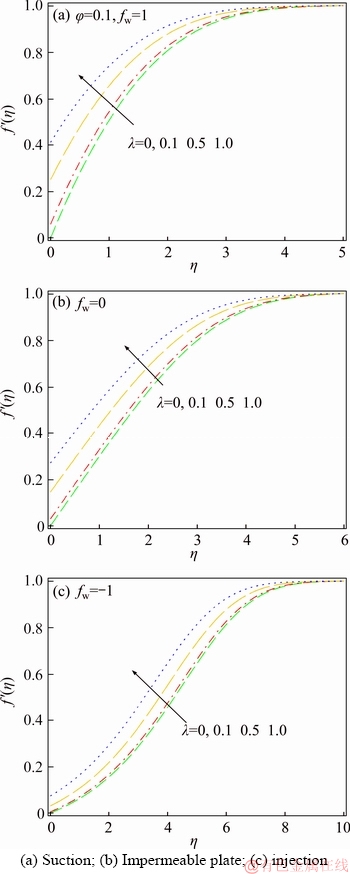
Figure 5 Slip velocity parameter influences on velocity profiles:
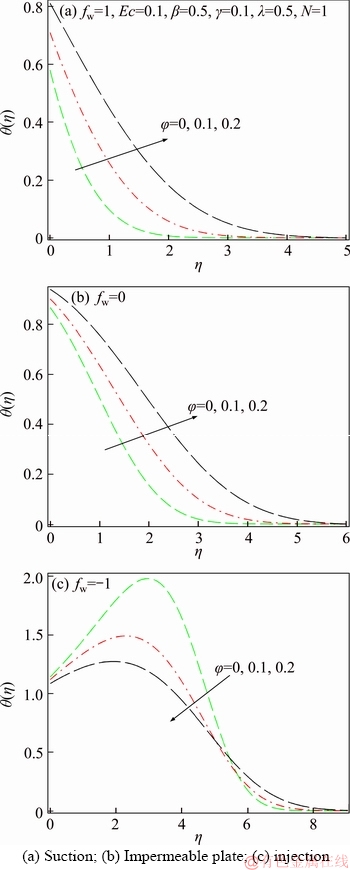
Figure 6 Effect of nanoparticles volume fraction on temperature distribution:
The impacts of suction/ injection on the velocity distribution are shown in Figure 4. Obviously, while boundary layer thickness experiences a reduction by raising the suction parameter, the velocity and velocity gradient are increased in near the surface. The reverse of above procedure is observed by the increase of injection parameter.

Figure 7 Permeability (suction/injection) effects on temperature distribution

Figure 8 Temperature distribution for different values of Eckert number:

Figure 9 Absorption/generation parameter effect on temperature distribution:
The relationship between the slip velocity parameter and the velocity profiles are shown in Figures 5 (a)–(c). In all studied cases, rising the slip velocity parameter leads to reducing the boundary layer thickness. In addition, velocity gradient at the surface is declined by increasing the slip velocity parameter in both cases of impermeable plate and suction; while, it increases in the case of injection. Moreover, the impact of slip velocity parameter in the case of suction is higher than two other studied cases.
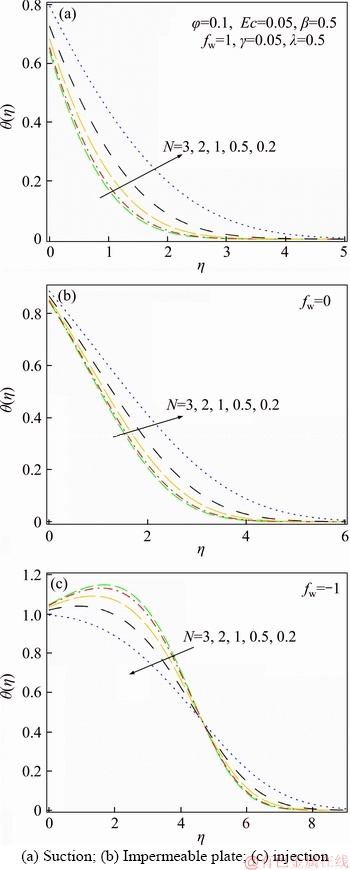
Figure 10 Radiation parameter efficacy on temperature profiles:
4.2 Influence of parameters alteration on temperature profiles
Figures 6(a)–(c) demonstrates the impacts of nanoparticles volume fraction on temperature distributions. For suction and impermeable plate cases, raising nanoparticles volume fraction leads to enhancing the dimensionless temperature. In the case of injection, dimensionless temperature distribution on the wall is unusual. In fact, due to the poor heat transfer characteristics in the case of injection, the fluid temperature near the wall increases in the presence of heat generation, radiation and viscous dissipation. As a result, the maximum fluid temperature occurs at the fluid layer near the wall instead of the wall. Also, in all cases, thermal boundary layer thickness rises with the augmentation of nanoparticles volume fraction.
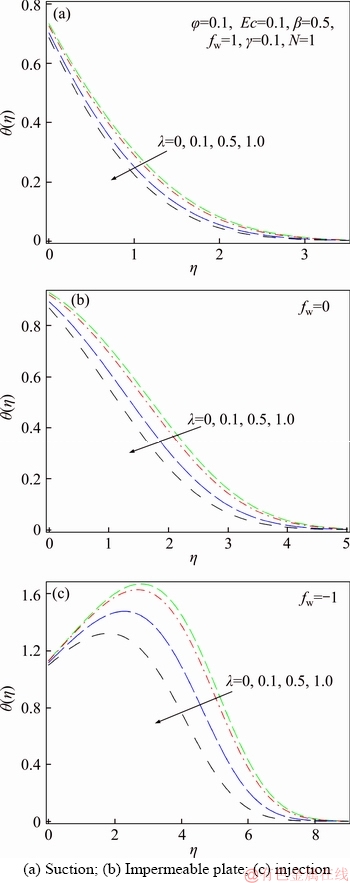
Figure 11 Temperature profiles for various values of slip velocity parameter:
The impact of suction or injection on the temperature profiles is shown in Figure 7. It is clear that raising the suction parameter will lead to a reduction in thermal boundary layer thickness.
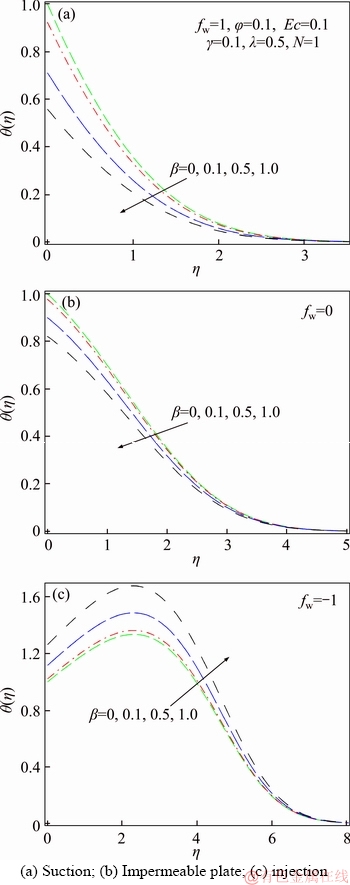
Figure 12 Thermal slip parameter impact on temperature distribution:
However, there is an increment in the temperature gradient in the surface. Furthermore, for the high injection parameter in the presence of radiation, heat generation and viscous dissipation, temperature gradient near the surface is positive which shows the heat transfers from the fluid to the surface. In addition, intensifying the injection parameter leads to the thermal boundary layer thickness enhancement.
The impacts of Eckert number on temperature profiles are demonstrated in Figures 8(a)–(c). In all cases, increasing the Eckert number reduces dimensionless temperature; while the impact of this parameter on the thermal boundary layer thickness is negligible.
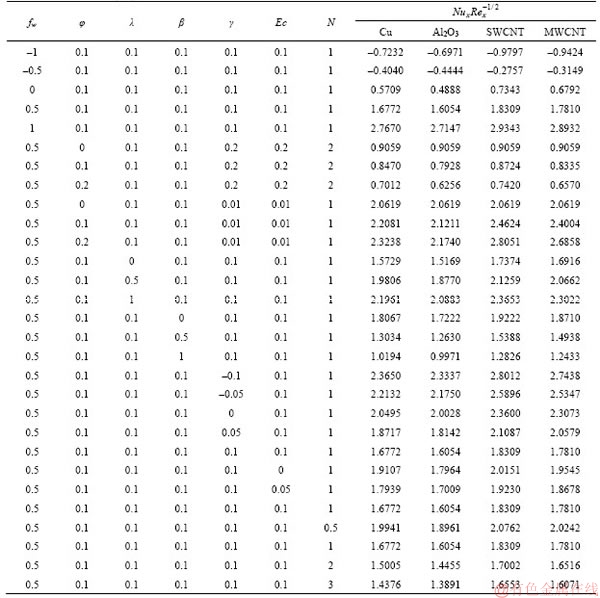
Table 2 Variation of 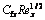 under impact of various parameters
under impact of various parameters

Figures 9(a)–(c) illustrate the impact of heat absorption or generation parameter on dimensionless temperature. As can be seen from the figure, dimensionless temperature increases by rising of heat generation parameter. However, it shows a decrease by increasing heat absorption parameter in the suction and impermeable plate cases. Furthermore, dimensionless temperature and temperature gradient in the surface are increased by raising the heat generation parameter in the case of injection. In injection case with heat generation, temperature gradient is positive and heat transfer direction is from fluid to the surface which indicates the importance of heat generation on the thermal behavior of the permeable plate.
Figures 10(a)–(c) demonstrate the impact of radiation parameter on the temperature distributions. This figure confirms that in the cases of suction and impermeable plate, dimensionless temperature and boundary layer thickness are diminished by boosting the radiation parameter. In addition, in the case of injection, the dimensionless temperature is increased near the wall, by increasing the radiation parameter; while decreasing this parameter expands the thickness of the boundary layer. Also, in the case of injection, reducing the radiation parameter can make the alteration in temperature gradient and consequently, thermal behavior at the wall.
Figures 11(a)–(c) and 12(a)–(c) represent the impacts of slip velocity (λ) and thermal slip (β) parameters on the temperature profiles. Figures 11 and 12 show that in all studied cases, by raising the slip velocity, the dimensionless temperature dropped. In addition, for impermeable plate and suction cases, dimensionless temperature was diminished by boosting the thermal slip parameter. The above phenomenon is reversed for injection case. Also, the highest impacts on the surface temperature for the variation of velocity and thermal slip parameters are observed for the cases of impermeable plate and suction, respectively.
4.3 Impact of parameters altering on local skin- friction and local Nusselt number
Table 2 shows the effects of nanomaterials types, nanoparticles volume fraction, slip velocity and suction or injection parameter on values of 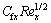 . It is concluded from Table 2 that the local skin-friction factor drops by slip velocity augmentation. Moreover, local skin-friction factor lessens by injection of fluid into the boundary layer; while it increases by boosting the suction parameter. In addition, local skin-friction coefficient has a raising trend by increasing the nanoparticles volume fraction for impermeable plate and suction cases; while the opposite trend is perceived for the injection case. Furthermore, carbon-based nanomaterials have lower skin friction coefficient than metal and metal-oxide nanomaterials while the nanofluids containing copper nanoparticles exhibit the highest skin friction coefficient for suction, impermeable plate and low-rate injection (fw≤–0.5) cases. For suction and impermeable plate cases, the lowest skin friction coefficients are observed for nanofluids including MWCNTs.
. It is concluded from Table 2 that the local skin-friction factor drops by slip velocity augmentation. Moreover, local skin-friction factor lessens by injection of fluid into the boundary layer; while it increases by boosting the suction parameter. In addition, local skin-friction coefficient has a raising trend by increasing the nanoparticles volume fraction for impermeable plate and suction cases; while the opposite trend is perceived for the injection case. Furthermore, carbon-based nanomaterials have lower skin friction coefficient than metal and metal-oxide nanomaterials while the nanofluids containing copper nanoparticles exhibit the highest skin friction coefficient for suction, impermeable plate and low-rate injection (fw≤–0.5) cases. For suction and impermeable plate cases, the lowest skin friction coefficients are observed for nanofluids including MWCNTs.
Table 3 displays the impacts of nanomaterials types, nanoparticles volume fraction, the Eckert number, suction or injection, heat generation or absorption, thermal slip, slip velocity and radiation parameters on values of 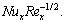 It is proved that the slip velocity or the suction parameter has a direct effect on the local Nusselt number but the injection or thermal slip parameters has the reverse influence on local Nusselt number. In the case of suction or impermeable plate, rising the heat generation, Eckert number and radiation parameter leads to a lower local Nusselt number since the mechanism increases the fluid temperature next to the surface, and consequently, temperature gradient at the surface shows a drop as a result of decreasing the surface heat transfer rate. On the other hand, there is a direct relationship between local Nusselt number and heat absorption since raising the heat absorption generates a cold fluid layer close to the surface. Studying the effects of nanoparticles volume fraction, Eckert number, radiation or heat generation parameter on the local Nusselt number confirms that there is a decline in the local Nusselt number by growth of nanoparticles volume fraction; while the opposite trend is apperceived for the typical values of Eckert number, heat generation or radiation parameter. As shown in Table 3, in the case of suction and impermeable plate, the minimum local Nusselt number belongs to Al2O3-water nanofluids and the maximum one belongs to SWCNTs-water. Considering the influence of large quantities of Eckert number, heat generation or radiation parameters, Cu-water nanofluids have higher Nusselt number than MWCNTs-water. This is while the thermal conductivity of Cu nanoparticles is 7.5 times fewer than the thermal conductivity of MWCNTs.
It is proved that the slip velocity or the suction parameter has a direct effect on the local Nusselt number but the injection or thermal slip parameters has the reverse influence on local Nusselt number. In the case of suction or impermeable plate, rising the heat generation, Eckert number and radiation parameter leads to a lower local Nusselt number since the mechanism increases the fluid temperature next to the surface, and consequently, temperature gradient at the surface shows a drop as a result of decreasing the surface heat transfer rate. On the other hand, there is a direct relationship between local Nusselt number and heat absorption since raising the heat absorption generates a cold fluid layer close to the surface. Studying the effects of nanoparticles volume fraction, Eckert number, radiation or heat generation parameter on the local Nusselt number confirms that there is a decline in the local Nusselt number by growth of nanoparticles volume fraction; while the opposite trend is apperceived for the typical values of Eckert number, heat generation or radiation parameter. As shown in Table 3, in the case of suction and impermeable plate, the minimum local Nusselt number belongs to Al2O3-water nanofluids and the maximum one belongs to SWCNTs-water. Considering the influence of large quantities of Eckert number, heat generation or radiation parameters, Cu-water nanofluids have higher Nusselt number than MWCNTs-water. This is while the thermal conductivity of Cu nanoparticles is 7.5 times fewer than the thermal conductivity of MWCNTs.
5 Conclusions
Boundary layer flow and heat transfer of nanofluids over a permeable plate are studied in details to elucidate the effects of different parameters including viscous dissipation, thermal radiation and heat generation/absorption by considering slip conditions at the boundary. The investigation showed a contradiction results with the outcomes of other researchers. This study confirms that in some cases, increasing the volume fraction of nanoparticles has a potential to reduce the heat transfer rate, due to changing the significant parameters including radiation, heat generation and viscous dissipation. Other results in summary are as below:
1) Local skin-friction coefficient increases by nanoparticles volume fraction augmentation for all studied nanofluids and in the case of suction and impermeable plate.
Table 3 Values of 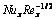 by altering different parameters
by altering different parameters
2) Slip velocity and injection parameter increment lead to a decrement in local skin-friction coefficient. However, it is boosted by rising of the suction parameter.
3) Cu-water nanofluids exhibit the highest skin friction coefficient for suction, impermeable plate and low-rate injection cases. While, the lowest values of skin friction coefficient are observed for nanofluids including MWCNTs.
4) The local Nusselt number diminishes by decreasing the slip velocity or suction parameter. However, boosting the Eckert number or injection, heat generation, radiation and thermal slip parameters result in local Nusselt number reduction.
5) For high values of Eckert number, heat generation or radiation parameter, the local Nusselt number is declined by an increment of nanoparticles volume fraction. In these circumstances, MWCNTs-water have the lower Nusselt numbers, compared to Cu-water nanofluids.
6) For impermeable plate and suction cases, the lowest local Nusselt number is observed for Al2O3-water nanofluids; while the largest Nusselt number is achieved for nanofluids containing SWCNTs.
Author contributions
Conceptualization, formal analysis, investigation, methodology, software, validation and visualization are done by Hamid MALEKI. Writing the original draft and editing are done by Jalal ALSARRAF and Abbas MOGHANIZADEH. Project administration, supervision and resources are provided by Mohammad Reza SAFAEI and Hassan HAJABDOLLAHI. All the authors have read and approved the final manuscript.
Nomenclature
Cp
Specific heat at constant pressure, J/(kg·K)
Cfx
Local skin-friction coefficient
Ec
Eckert number
f
Dimensionless stream function
fw
Transpiration rate constant
k
Thermal conductivity, W/(m·K)
k*
Mean absorption coefficient, m–1
N
Radiation parameter
Nux
Local Nusselt number
Pr
Prandtl number
Q0
Heat generation/absorption
coefficient, J/(m3·K·s)
qr
qw
Radiative heat flux, W/m2
Surface heat flux, W/m2
Rex
Local Reynolds number
T
Fluid temperature, K
U
Velocity, m/s
u, v
Velocity components along x and y directions, m/s
vw
Mass transfer velocity at the surface, m/s
x
Coordinate along the plate, m
y
Coordinate normal to the plate, m
CNT
Carbon nanotube
SWCNTs
Single-wall carbon nanotubes
MWCNTs
Multi-wall carbon nanotubes
ODE
Ordinary differential equation
PDE
Partial differential equation
Greek symbols
a
Thermal diffusivity, m2/s
h
Similarity variable
q
Dimensionless temperature
l
Velocity ratio parameter
m
Dynamic viscosity, kg/(m·s)
n
Kinematic viscosity, m2/s
r
Fluid density, kg/m3
σ
Stephan–Boltzmann constant,
W/(m2·K4)
τw
Surface shear stress, kg/(m·s2)
j
Nanoparticles volume fraction
g
Local heat generation/absorption parameter
y
Stream function
Subscripts
f
Fluid
w
Condition at the surface

Ambient condition
nf
Nanofluid
s
Solid
References
[1] HAJMOHAMMADI M R, MALEKI H, LORENZINI G, NOURAZAR S S. Effects of Cu and Ag nano-particles on flow and heat transfer from permeable surfaces [J]. Advanced Powder Technology, 2015, 26(1): 193–199.
[2] ISHAK A. Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition [J]. Applied Mathematics and Computation, 2010, 217(2): 837–842.
[3] ISAIAH O O, ALFRED M W, JACOB B K. MHD stokes heat and mass flow past an infinite permeable plate subjected to convective surface boundary conditions [J]. International Journal of Contemporary Mathematical Sciences, 2017, 12(3): 139–154.
[4] CHODHURY R, DEY B. Flow features of a conducting visco-elastic fluid past a vertical permeable plate [J]. Global Journal of Pure and Applied Mathematics, 2017, 13(9): 5687–5702.
[5] SADRI S, BABAELAHI M. Analysis of a laminar boundary layer flow over a flat plate with injection or suction [J]. Journal of Applied Mechanics and Technical Physics, 2013, 54(1): 59–67.
[6] YASIN M H I, ISHAK A, POP I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect [J]. Journal of Magnetism and Magnetic Materials, 2016, 407: 235–240.
[7] RAJU M C, CHAMKHA A J, PHILIP J, VARMA S V. Soret effect due to mixed convection on unsteady magnetohydrodynamic flow past a semi-infinite vertical permeable moving plate in presence of thermal radiation, heat absorption and homogenous chemical reaction [J]. International Journal of Applied and Computational Mathematics, 2017, 3(2): 947–961.
[8] SINGH G, MAKINDE O D. Mixed convection slip flow with temperature jump along a moving plate in presence of free stream [J]. Thermal Science, 2015, 19(1): 119–128.
[9] EEGUNJOBI A S, MAKINDE O D, JANGILI S. Unsteady MHD chemically reacting and radiating mixed convection slip flow past a stretching surface in a porous medium [J]. In Defect and Diffusion Forum, 2017, 377: 200–210.
[10] MUHAMMAD A, MAKINDE O D. Thermodynamics analysis of unsteady MHD mixed convection with slip and thermal radiation over a permeable surface [J]. In Defect and Diffusion Forum, 2017, 374: 29–46.
[11] HEYDARI A, AKBARI O A, SAFAEI M R, DERAKHSHANI M, ALRASHED A A, MASHAYEKHI R, SHABANI G A, ZARRINGHALAM M, NGUYEN T K. The effect of attack angle of triangular ribs on heat transfer of nanofluids in a microchannel [J]. Journal of Thermal Analysis and Calorimetry, 2018, 131(3): 2893–2912.
[12] MAGHSOUDI P, SIAVASHI M. Application of nanofluid and optimization of pore size arrangement of heterogeneous porous media to enhance mixed convection inside a two-sided lid-driven cavity [J]. Journal of Thermal Analysis and Calorimetry, 2018, 135(2): 947–961.
[13] MALEKI H, SAFAEI M R, ALRASHED A A, KASAEIAN A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces [J]. Journal of Thermal Analysis and Calorimetry, 2019, 135(3): 1655–1666.
[14] KHAMLICHE T, KHAMLICH S, DOYLE T B, MAKINDE O D, MAAZA M. Thermal conductivity enhancement of nano-silver particles dispersed ethylene glycol based nanofluids [J]. Materials Research Express, 2018, 5(3): 035020.
[15] SARI M R, KEZZAR M, ADJABI R. Heat transfer of copper/water nanofluid flow through converging-diverging channel [J]. Journal of Central South University, 2016, 23(2): 484–496.
[16] MALEKI H, SAFAEI MR, TOGUN H, DAHARI M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation [J]. Journal of Thermal Analysis and Calorimetry, 2019, 135(3): 1643–1654.
[17] SAFAEI M R, KARIMIPOUR A, ABDOLLAHI A, NGUYEN T K. The investigation of thermal radiation and free convection heat transfer mechanisms of nanofluid inside a shallow cavity by lattice Boltzmann method [J]. Physica A: Statistical Mechanics and Its Applications, 2018, 509: 515–535.
[18] ABBASSI M A, SAFAEI M R, DJEBALI R, GUEDRI K, ZEGHMATI B, ALRASHED A A A. LBM simulation of free convection in a nanofluid filled incinerator containing a hot block [J].International Journal of Mechanical Sciences, 2018, 144: 172–185.
[19] SIAVASHI M, JAMALI M. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24(8): 1850–1865.
[20] ALRASHED A A A, GHARIBDOUSTI M S, GOODARZI M, de OLIVEIRA L R, SAFAEI M R, BANDARRA F E P. Effects on thermophysical properties of carbon based nanofluids: Experimental data, modelling using regression, ANFIS and ANN [J]. International Journal of Heat and Mass Transfer, 2018, 125: 920–932.
[21] ARANI A A A, AKBARI O A, SAFAEI M R, MARZBAN A, ALRASHED A A A, AHMADI G R, NGUYEN T K. Heat transfer improvement of water/single-wall carbon nanotubes (SWCNT) nanofluid in a novel design of a truncated double-layered microchannel heat sink [J]. International Journal of Heat and Mass Transfer, 2017, 113: 780–795.
[22] ALRASHED A A A A, AKBARI O A, HEYDARI A, TOGHRAIE D, ZARRINGHALAM M, SHABANI G A S, SEIFI A R, GOODARZI M. The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel [J]. Physica B: Condensed Matter, 2018, 537: 176–183.
[23] SIAVASHI M, GHASEMI K, YOUSOFVAND R, DERAKHSHAN S. Computational analysis of SWCNH nanofluid-based direct absorption solar collector with a metal sheet [J]. Solar Energy, 2018, 170: 252–262.
[24] GUPTA M, SINGH V, KUMAR R, SAID Z. A review on thermophysical properties of nanofluids and heat transfer applications [J]. Renewable and Sustainable Energy Reviews, 2017, 74: 638–670.
[25] AHMED A, NADEEM S. Biomathematical study of time-dependent flow of a Carreau nanofluid through inclined catheterized arteries with overlapping stenosis [J]. Journal of Central South University, 2017, 24(11): 2725–2744.
[26] BAHIRAEI M, JAMSHIDMOFID M, GOODARZI M. Efficacy of a hybrid nanofluid in a new microchannel heat sink equipped with both secondary channels and ribs [J]. Journal of Molecular Liquids, 2019, 273: 88–98.
[27] MAHMOODI M, KANDELOUSI S. Kerosene-alumina nanofluid flow and heat transfer for cooling application [J]. Journal of Central South University, 2016, 23(4): 983–990.
[28] SIAVASHI M, RASAM H, IZADI A. Similarity solution of air and nanofluid impingement cooling of a cylindrical porous heat sink [J]. Journal of Thermal Analysis and Calorimetry, 2019, 135(2): 1399–1415.
[29] BAHMANI M H, SHEIKHZADEH G, ZARRINGHALAM M, AKBARI O A, ALRASHED A A, SHABANI G A, GOODARZI M. Investigation of turbulent heat transfer and nanofluid flow in a double pipe heat exchanger [J]. Advanced Powder Technology, 2018, 29(2): 273–282.
[30] KHODABANDEH E, SAFAEI M R, AKBARI S, AKBARI O A, ALRASHED A A A. Application of nanofluid to improve the thermal performance of horizontal spiral coil utilized in solar ponds: Geometric study [J]. Renewable Energy, 2018, 122: 1–16.
[31] DAS K, CHAKRABORTY T, KUMAR K P. Slip effects on nanofluid flow over a nonlinear permeable stretching surface with chemical reaction [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2016, 230(14): 2473–2482.
[32] ZIAEI-RAD M, KASAEIPOOR A, RASHIDI M M, LORENZINI G. A similarity solution for mixed-convection boundary layer nanofluid flow on an inclined permeable surface [J]. Journal of Thermal Science and Engineering Applications, 2017, 9(2): 021015.
[33] MOHAMMDIEN S A, RASLAN K, ABDEL-WAHED M S, ABEDEL-AAL E M. KKL-model of MHD CuO-nanofluid flow over a stagnation point stretching sheet with nonlinear thermal radiation and suction/injection [J]. Results in Physics, 2018, 10: 194–199.
[34] NANDEPPANAVAR M M, REDDY G R S, SHAKUNTHALA S. Magneto-hydrodynamic Blasius flow and heat transfer from a flat plate in the presence of suspended carbon nanofluids [J]. Proceedings of the Institution of Mechanical Engineers, Part N: Journal of Nanomaterials, Nanoengineering and Nanosystems, 2018, 232(1): 31–40.
[35] ETWIRE C J, SEINI I Y, MUSAH R, MAKINDE O D. Combined effects of variable viscosity and thermal conductivity on dissipative flow of oil-based nanofluid over a permeable vertical surface [J]. In Diffusion Foundations, 2018, 16: 158–176.
[36] NAYAK M K. MHD 3D flow and heat transfer analysis of nanofluid by shrinking surface inspired by thermal radiation and viscous dissipation [J]. International Journal of Mechanical Sciences, 2017, 124: 185–193.
[37] HAYAT T, KHAN M I, FAROOQ M, ALSAEDI A, YASMEEN T. Impact of Marangoni convection in the flow of carbon–water nanofluid with thermal radiation [J]. International Journal of Heat and Mass Transfer, 2017, 106: 810–815.
[38] MAKINDE O D. Effects of viscous dissipation and Newtonian heating on boundary-layer flow of nanofluids over a flat plate [J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2013, 23(8): 1291–1303.
[39] ZAIB A, BHATTACHARYYA K, SHAFIE S. Unsteady boundary layer flow and heat transfer over an exponentially shrinking sheet with suction in a copper-water nanofluid [J]. Journal of Central South University, 2015, 22(12): 4856–4863.
[40] MAKINDE O D, KHAN W A, KHAN Z H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet [J]. International Journal of Heat and Mass Transfer, 2013, 62: 526–533.
[41] BACHOK N, ISHAK A, POP I. Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet [J]. International Journal of Heat and Mass Transfer, 2012, 55(7, 8): 2102–2109.
[42] BHATTACHARYYA K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet [J]. International Communications in Heat and Mass Transfer, 2011, 38(7): 917–922.
[43] YAO S, FANG T, ZHONG Y. Heat transfer of a generalized stretching/shrinking wall problem with convective boundary conditions [J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(2): 752–760.
[44] PAL D, MANDAL G. Mixed convection–radiation on stagnation-point flow of nanofluids over a stretching/ shrinking sheet in a porous medium with heat generation and viscous dissipation [J]. Journal of Petroleum Science and Engineering, 2015, 126: 16–25.
[45] MANSUR S, ISHAK A, POP I. The magnetohydrodynamic stagnation point flow of a nanofluid over a stretching/shrinking sheet with suction [J]. PLoS One, 2015, 10(3): 0117733.
[46] ZAIMI K, ISHAK A, POP I. Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid [J]. Scientific Reports, 2014, 4: 4404.
[47] UDDIN M J, B G O A, ISMAIL A I. Radiative convective nanofluid flow past a stretching/shrinking sheet with slip effects [J]. Journal of Thermophysics and Heat Transfer, 2015, 29(3): 513–523.
G O A, ISMAIL A I. Radiative convective nanofluid flow past a stretching/shrinking sheet with slip effects [J]. Journal of Thermophysics and Heat Transfer, 2015, 29(3): 513–523.
[48] AZIZ A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(4): 1064–1068.
[49] ABU-NADA E. Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step [J]. International Journal of Heat and Fluid Flow, 2008, 29(1): 242–249.
[50] KHAN W A, KHAN Z H, RAHI M. Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary [J]. Applied Nanoscience, 2014, 4(5): 633–641.
[51] TIWARI R K, DAS M K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids [J]. International Journal of Heat and Mass Transfer, 2007, 50(9, 10): 2002–2018.
[52] OZTOP H F, ABU-NADA E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids [J]. International Journal of Heat and Fluid Flow, 2008, 29(5): 1326–1336.
[53] FORABOSCHI F P, DI F I. Heat transfer in laminar flow of non-Newtonian heat-generating fluids [J]. International Journal of Heat and Mass Transfer, 1964, 7(3): 315–325.
[54] MAHMOUD M A A, MEGAHED A M. Effects of suction and injection on MHD heat transfer in an electrically conducting fluid at a stretching vertical plate embedded in a porous medium with uniform free stream [J]. Nuovo Cimento-B, 2006, 121(9): 923–936.
[55] MOTSUMI T G, MAKINDE O D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate [J]. Physica Scripta, 2012, 86(4): 045003.
[56] BRINKMAN H C. The viscosity of concentrated suspensions and solutions [J]. The Journal of Chemical Physics, 1952, 20(4): 571.
[57] MAXWELL JAMES CLERK. A treatise on electricity and magnetism [M]. Clarendon Press, 1881.
[58] MURSHED S M S, de CASTRO C N. Superior thermal features of carbon nanotubes-based nanofluids–A review [J]. Renewable and Sustainable Energy Reviews, 2014, 37: 155–167.
[59] XUE Q Z. Model for thermal conductivity of carbon nanotube-based composites [J]. Physica B: Condensed Matter, 2005, 368(1–4): 302–307.
[60] GHADIKOLAEI S S, HOSSEINZADEH K, HATAMI M, GANJI D D, ARMIN M. Investigation for squeezing flow of ethylene glycol (C2H6O2) carbon nanotubes (CNTs) in rotating stretching channel with nonlinear thermal radiation [J]. Journal of Molecular Liquids, 2018, 263: 10–21.
[61] FAROOQ S, HAYAT T, ALSAEDI A, ASGHAR S. Mixed convection peristalsis of carbon nanotubes with thermal radiation and entropy generation [J]. Journal of Molecular Liquids, 2018, 250: 451–467.
[62] HAYAT T, NASIR T, KHAN M I, ALSAEDI A. Non-Darcy flow of water-based single (SWCNTs) and multiple (MWCNTs) walls carbon nanotubes with multiple slip conditions due to rotating disk [J]. Results in Physics, 2018, 9: 390–399.
[63] AL-RASHED A A A A, KALIDASAN K, KOLSI L, AYDI A, MALEKSHAH E H, HUSSEIN A K, KANNA P R. Three-dimensional investigation of the effects of external magnetic field inclination on laminar natural convection heat transfer in CNT–water nanofluid filled cavity [J]. Journal of Molecular Liquids, 2018, 252: 454–468.
[64] CORTELL R. Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet [J]. Physics Letters A, 2008, 372(5): 631–636.
[65] RAPTIS A, PERDIKIS C, TAKHAR H S. Effect of thermal radiation on MHD flow [J]. Applied Mathematics and Computation, 2004, 153(3): 645–649.
[66] JAVED M, FAROOQ M, AHMAD S, ANJUM A. Melting heat transfer with radiative effects and homogeneous– heterogeneous reaction in thermally stratified stagnation flow embedded in porous medium [J]. Journal of Central South University, 2018, 25(11): 2701–2711.
(Edited by YANG Hua)
中文导读
辐射滑移边界条件下多孔板上的传热与纳米流体流动
摘要:考虑多孔表面上的纳米流体在不同时期不同值下可能会发生热性能变化。本研究的目的是研究纳米粒子的体积分数、纳米粒子的种类、吸入或注入、热的产生或吸收、Eckert数、热和速度滑移参数以及辐射对多孔平板上流体流动和传热的影响。研究了4种不同类型的纳米粒子,Cu纳米颗粒、Al2O3纳米粒子和碳基纳米材料(MWCNTs和SWCNTs), 分散在水中的情况。利用相似解将控制方程转化为常微分方程,并用RKF45算法进行数值求解。模拟结果与其他研究人员的结果相矛盾,其他研究人员认为,使用具有高导热系数的高体积分数的纳米粒子可提高纳米流体的传热速率;本研究证明,当辐射、热产生和粘滞耗散等参数值发生显著变化时,提高纳米粒子的体积分数可能会降低传热速率。
关键词:辐射;滑移条件;多孔表面;热产生/吸收;黏性耗散;纳米流体
Received date: 2018-09-14; Accepted date: 2019-01-03
Corresponding author: Mohammad Reza SAFAEI, PhD; Tel: +1-502-657-9981; E-mail: cfd_safaei@tdtu.edu.vn; ORCID: 0000-0001- 7301-2561

