J. Cent. South Univ. (2012) 19: 1988-1998
DOI: 10.1007/s11771-012-1236-6
An elasto-plastic constitutive model incorporating strain softening and
dilatancy for interface thin-layer element and its verification
PENG Kai (彭凯)1, 2, 3, ZHU Jun-gao(朱俊高)2, 3, FENG Shu-rong(冯树荣)1,
WANG Rong(王荣)2, 3, LIU Han-long(刘汉龙)2, 3
1. Hydrochina Zhongnan Engineering Corporation, Changsha 410014, China;
2. Key Laboratory of Geo-mechanics and Embankment Engineering of Ministry of Education
(Hohai University), Nanjing 210098, China;
3. Geotechnical Research Institute, Hohai University, Nanjing 210098, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The mechanical behaviors of the interface between coarse-grained soil and concrete were investigated by simple shear tests under condition of mixed soil slurry (bentonite mixed with cement grout). For comparison, the interfaces both without slurry and with bentonite slurry were analyzed. The experimental results show that different slurries exert much influence on the strength and deformation of soil/structure interface. Under mixed soil slurry, strain softening and shear dilatation are observed, while shear dilatation appears under the small normal stress of the interface without slurry, and shear contraction is significant under the condition of the bentonite slurry. The thickness of the interface was determined by analyzing the disturbed height of the sample with both simple shear test and particle flow code (PFC). An elasto-plastic constitutive model incorporating strain softening and dilatancy for thin layer element of interface was formulated in the framework of generalized potential theory. The relation curves of shear stress and shear strain, as well as the relation curves of normal strain and shear strain, were fitted by a piecewise function composed by hyperbolic functions and resembling normal functions. The entire model parameters can be identified by tests. The new model is verified by comparing the measured data of indoor cut-off wall model tests with the predictions from finite element method (FEM). The FEM results indicate that the stress of wall calculated by using Goodman element is too large, and the maximum deviation between the test data and prediction is about 45%. While the prediction from the proposed model is close to the measured data, and the error is generally less than 10%.
Key words: simple shear test; mixed soil slurry; dilatancy; particle flow code; generalized potential theory; constitutive model; FEM
1 Introduction
Soil-structure interaction (SSI) has been an active research topic in geotechnical engineering for many years [1-8]. So far, some researchers have already studied and made a lot of achievements on basic rules, influencing factors and simulation analysis methods of soil/structure interface [9-14]. BOULON and PLYTAS [15] developed a constitutive model based on the results of direct shear test under constant normal load and constant volume. DESAI and PRADHAN [16] presented a modeling approach called disturbed-state concept. MORTARA et al [17] proposed a new elasto-plastic model for interface between sand and rigid structures, and it has been formulated in terms of interface stresses and relative displacements. GENNARO and FRANK [18] presented an elasto-plastic model on purpose of describing the granular media structure interface. CABALLERO et al [19] developed a model to simulate the behavior of three dimensional interfaces. In addition, PASTER et al [20] developed a constitutive modeling which used loading direction vector and plastic flow direction vector instead of yield and plastic potential function based on the generalized theory of plastic. YANG [21] advised a new method to build soil constitutive model in mathematic way and presented a generalized potential theory which is easy to apply in building model.
YIN et al [22] observed deformation of the interface with micro periscope and regarded that damage of the interface is a gradual extending process from side to interior. ZHANG et al [23] analyzed influence of variation of slurry thickness and water content on coarse-grained soil/concrete interface. ZHANG and ZHANG [24] studied static and dynamic characteristics of interface and influence of different shear modes on the interface. ZHANG et al [25] analyzed the influence of mudcake on shaft friction and the difference between mudcake and soil between bored piles. PENG et al [26] studied mechanical behaviors of interface between coarse-grained soil and concrete by simple shear tests. In addition, many researches used particle flow code (PFC) to study the geotechnical tests [27-29]. YANG et al [30-33] applied modified image analytical solutions to predict the nonlinear displacement of interface with the nonuniform form convergence model in tunneling and underground space field.
In actual engineering, due to construction technology, slurry, especially mixed soil slurry, between cut-off wall and coarse-grained soil always exists, which influences or changes mechanical properties of coarse-grained soil-structure. As a result, the load sharing ratio of the soil and concrete will change. It is significant to investigate and predict the interface behavior.
In this work, the behavior of the interface under conditions without slurry, with bentonite slurry and with mixed soil slurry (doping cement to bentonite slurry) were studied by using simple shear tests, and the thickness of the interface was analyzed by PFC. Based on the mechanical response of the interface under mixed soil slurry, a constitutive model was presented and extended to 3D space.
2 Test results and analysis
2.1 Apparatus, materials and methods
A large-scale simple shear apparatus was employed to perform the simple shear test (SST) on three types of interfaces, i.e. without slurry, with bentonite slurry and with mixed soil slurry. The sketch of the apparatus is shown in Fig. 1(a). The inner diameter of each stacked ring is 300 mm, and the thickness of soil sample is 20 mm. The total effective height of sample including the concrete plate is 120 mm. In the test, normal stress (σn) is kept constant; shear displacement (δ) and shear stress (τ) are increased gradually. The shear strain (γ) within certain thickness (t) is expressed as
τ=T/S, σn=P/A, γ=δ/t (1)
where P and T refer to the vertical and horizontal loads, respectively, A is the area and t refers to the thickness of the interface between soil and concrete, as shown in Fig. 1(b).
The maximum diameter of the coarse-grained soil tested is 20 mm. The grading curve is shown in Fig. 2. The dry density and relative density of soil sample are 2.13 g/cm3 and 0.9, respectively.
The mixed soil slurry is composed of bentonite slurry and cement slurry. The cement content in the mixed soil slurry was 15%, and the ratio of water cement to cement slurry was 1.5:0.5. The tests were conducted until mixed soil slurry was cured after 28 d. The density and water content of the bentonite slurry were 1.28 g/cm3 and 40%, respectively. The pre-prepared slurry is shown in Fig. 3.

Fig. 1 Schematic diagrams of simple shear box and force of interface sample: (a) Experimental equipment; (b) Force and deformation of sample

Fig. 2 Size grading curve of aggregate
The surface of the concrete was coarse. In view of 20 mm-thick single stacked ring, the thickness of slurry was made to be 20 mm so as to better reflect the deformation of the interface during the shear process. The normal stresses were 200, 500, 1 200 and 2 000 kPa, respectively, and the shear rate was 0.3 mm/min.

Fig. 3 Pre-prepared slurry: (a) Bentonite slurry; (b) Mixed soil slurry
2.2 Shear strength and deformation behavior
Comparative tests were carried out under three conditions (without slurry, with bentonite slurry and with mixed soil slurry), and the influence of slurry on shear strength of the interface was investigated. The test results are shown in Figs. 4 and 5. In this work, shear contraction is taken to be the positive value and shear dilatancy is taken to be the negative value.
According to Figs. 4 and 5, the slurry plays an important influence on both the shear strength and the deformation of the interface. For the interface with mixed soil slurry, strain softening and dilatancy are evident. The peak strength and the corresponding shear strain are obviously related to the normal stress, and dilatancy occurs before the peak strength.
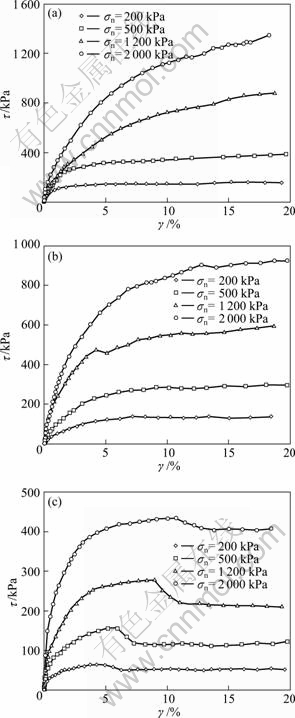
Fig. 4 Relationship between τ and γ: (a) Without slurry; (b) With bentonite slurry; (c) With mixed soil slurry
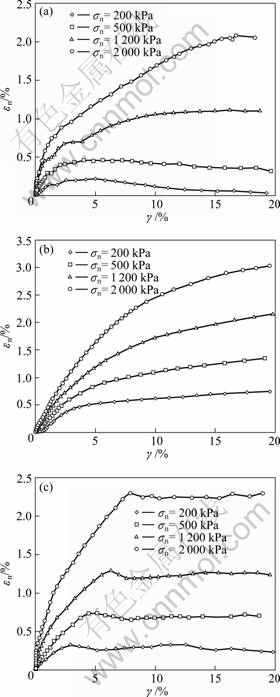
Fig. 5 Relationship between εn and γ: (a) Without slurry; (b) With bentonite slurry; (c) With mixed soil slurry
For interface without slurry, dilatancy is observed when the normal stress is small, such as 200 or 500 kPa, but it disappears for interface with bentonite slurry. Furthermore, the τ-γ curves of the interface show strain hardening in condition of both without slurry and with bentonite slurry.
Compared with the peak strength of interface without slurry, the peak strengths of interface with mixed soil slurry and bentonite slurry are decreased by 70% and 40%, respectively. As shown in Figs. 4(b) and 4(c), however, when the cement content is 15%, the shear strength of interface with mixed soil slurry is much less than that of interface with bentonite slurry. This phenomenon seems to be against with the theoretical analysis. During shearing, the bentonite slurry and coarse-grained soil are mixed together, and there is no complete bentonite slurry layer to prevent the coarse-grained soil from contacting concrete surface, as shown in Figs. 6(a) and (b). For mixed soil slurry, it is able to form complete layer to prevent soil contacting concrete directly, as shown in Figs. 6(c) and (d). As a result, its strength is smaller than that of bentonite slurry.

Fig. 6 Images of interface: (a) Bentonite slurry during pre-test; (b) Bentonite slurry during post-test; (c) Mixed soil slurry during pre-test; (d) Mixed soil slurry during post-test
Compression curves of different conditions are shown in Fig. 7. From Fig. 7, normal strain of interface without slurry is the minimum, bentonite slurry has the maximum value, and the mixed soil slurry is between them. The results are mainly caused by the phenomenon that part of bentonite slurry is pushed into the void of soil; of course, are also caused by the compression of the slurry.
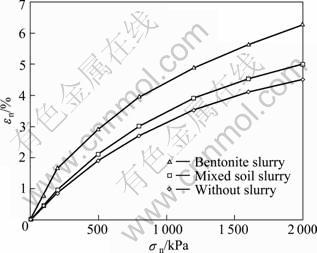
Fig. 7 Curves of compression under different conditions
2.3 Thickness of interface
During shear process, non-uniformity exists in the shear deformation. As shown in Fig. 8, the horizontal displacements of stacked rings are different, and the horizontal displacements already reach the top of the sample, that is to say, it is the disturbed height inside the sample. At this time, a thin layer interface element is formed. For thin layer element, the thickness of the interface is a critical issue. Some researchers advise that the thickness can be determined by defining the ratio of the thickness (t) to the width of the element (w), that is to say, the thickness will vary with the width of the element. In fact, the disturbed belt will not vary with w during the shear process. For a particular engineering, it is better determined by both test and numerical simulation.

Fig. 8 Shear displacement along height direction
Due to the limited height of the apparatus, the maximum disturbed height needs to be determined further. To determine the maximum disturbed height of the interface, laws of particle motion at different heights inside the sample are simulated during the shear process by particle flow code (PFC). The numerical experiment modeling of simple shear test is shown in Fig. 9.
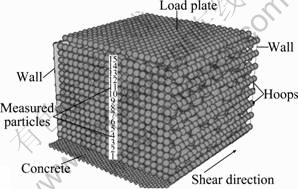
Fig. 9 Modeling of simple shear test
In Fig. 9, the size of the model is 40 cm (width) ×40 cm (length) ×30 cm (height). The top box is composed of three parts. First, wall unit is used for left and right sides. Then, along the shear direction, two rows of balls on the front and back sides adopted are designed to simulate horizontal displacement in different heights, but they could not produce vertical displacement. Besides, several hoops make up of balls in different heights, which are used to replace the stacked rings in simple shear test to simulate horizontal displacement. These hoops keep their shape and cannot produce shear deformation. For coarse-grained soil, particles are drawn from a uniform distribution of radius with the specified upper and lower limits of 10 mm and 5 mm, respectively, and porosity of 0.3. For slurry, the thickness is 20 mm, the radius of particle is 3 mm, and the porosity is 0.2. The shear rate is 0.3 mm/min.
For the coarse-grained soil the contact-stiffness model is used, for the bentonite slurry and the mixed soil slurry the contact bonds model is applied, and for other materials, such as two rows of balls on the front and back sides, hoops, concrete and load plate, the parallel bonds model is used. The main parameters of particle in simulation are listed in Table 1.
In Table 1, the Kn and Ks refer to normal and shear sitffnesses, respectively, for each ball. Kn,Pb and Ks,Pb are parallel-bond normal and shear stiffnesses, respectively. σn,Pb and σs,Pb refer to parallel-bond normal and shear strengths, respectively. τn,b and τs,b are contact bond normal strength and shear strength, respectively. MR is radius multiplier such that parallel-bond radius equals this multiplier times the minimum radius of the two bonded balls.
The properties of the interface without slurry, with bentonite slurry and with mixed slurry could be reflected by different friction coefficients (f) of the concrete, which can be determined by fitting the shear stress and normal strain, and their values are 0.55, 0.35 and 0.15, respectively. In addition, the influence on disturbed height due to different maximum particle diameters (d) is analyzed, and the results are shown in Fig. 10 when the normal stress is 2 000 kPa. The numbers such as 1, 5, 10, and 15 in Fig. 10 correspond to the numbers of the particles in Fig. 9, and the abscissa and vertical axes refer to calculation time step and horizontal displacement
of the measured particles with different heights.
As shown in Fig.10, disturbed height of the sample is related to the maximum particle diameter of the soil, normal stress and roughness of the interface. From bottom to top, the disturbance inside the sample decreases gradually. Close to the top, the horizontal displacement almost appears in horizontal line during shear process. Distinctly, the horizontal displacements of the measured particles can be neglected when the number exceeds 9 (from bottom to top). Given that the diameter of the ball is 2 cm, the disturbed height is around 18 cm. So, the thickness of the thin-layer element can be regarded as 18 cm in simulation.
3 Elasto-plastic constitutive model
3.1 Main equations of elasto-plastic constitutive model
In shear test, a two-dimensional relation between stress and strain can be obtained, that is, the relation between (σn, τ) and (εn, γ). In stress space, its 2D vectors are ε={εn, γ} and σ={σn, τ}, respectively. Therefore, according to the generalized potential theory and elasto-plastic theory [34], the mathematical expressions of relation between total stress and strain are
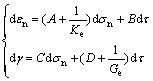 (2)
(2)
where Ge refers to tangential elastic modulus. Ke is normal elastic modulus, which is determined by simple compression curves and rebound curves. Further, Ge is determined when Poisson ratio is assumed to be 0.3. Then, the parameters of elasticity are obtained.
The coefficient matrix of Eq. (2) is composed of A, B, C and D. A is a coefficient reflecting compression caused by normal stress, B is a coupled coefficient, which reflects the influence on normal strain from shear stress, and D reflects shear behavior. Besides, generally, simple or direct shear test does not consider the shear deformation caused by normal stress, therefore, C=0. If all these coefficients are found, the constitutive model is then determined.
Table 1 Main parameters of particles in simulation

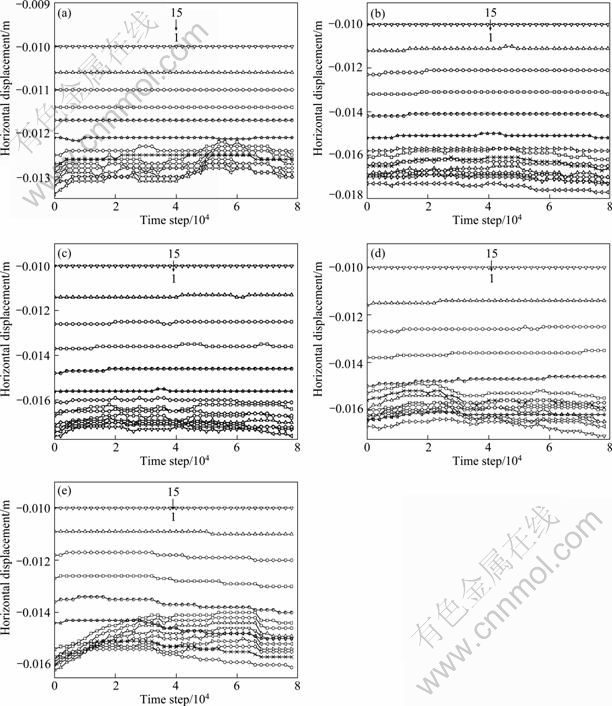
Fig. 10 Horizontal displacements of measured particles under different conditions: (a) Without slurry (f=0.55, d=2cm); (b) With bentonite slurry (f=0.35, d=2cm); (c) With mixed soil slurry (f=0.15, d=2 cm); (d) Influence of particle diameter (f=0.15, d=4 cm); (e) Influence of particle diameter (f=0.15, d=6 cm)
3.2 Model parameters of interface
The mechanical response of the interface is shown in Fig. 11 in the presence of mixed soil slurry. The plastic state equation is obtained by fitting the test results with piecewise function which is composed of hyperbolic function and resembling normal function. Eventually, parameters of the model are determined.
1) Determination of coefficient A
According to Fig. 7, assuming that the curve of uniaxial compression test obeys exponential function, then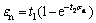 . From Eq. (2), one can further get
. From Eq. (2), one can further get 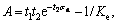 where t1 and t2 are fitting parameters, and σn refers to normal stress.
where t1 and t2 are fitting parameters, and σn refers to normal stress.
2) Determination of coefficient D
Assuming that τ-γ relation can be expressed by hyperbolic function and resembling normal function in different ranges of shear strain:
 (3)
(3)

where K and n refer to test parameters. γf is the shear strain corresponding to the peak strength τf, and it can be expressed as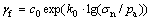 , where c0 and k0 are fitting parameters. In view of continuity of the function at γf,
, where c0 and k0 are fitting parameters. In view of continuity of the function at γf,  . From Mohr-Coulomb criterion,
. From Mohr-Coulomb criterion,  , is got.
, is got.
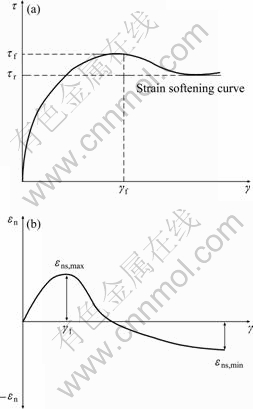
Fig. 11 Mechanical response of interface with mixed soil slurry: (a) Schematic diagram of τ-γ; (b) Schematic diagram of εn-γ
Residual strength τf in Eq. (3) can be expressed as τf=c′+σntanφ′, and α1 refers to the shape parameter which is determined by the softening stage relations of τ-γ under different normal stresses. Generally, α1 changes little with the different normal stresses. So, the average value is taken.
From Eq. (3) and Eq. (2), the coefficient D can be expressed as
 (4)
(4)
3) Determination of coefficient B
Assuming that
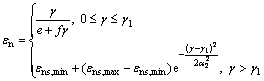 (5)
(5)
where γ1 is the shear strain corresponding to εns,max; εns,max and εns,min refer to maximum and minimum normal strain due to the shear (normal compression is positive), respectively; α2 is shape parameter of the function. According to the test results, it is found that the parameters of e, f, εns,max, εns,min and γ1 are functions of normal stress, and they can be given by
 (6)
(6)
where c0, c1, c2, c3, d0, d1, d2, d3, k0, k1, k2 and k3 are the parameters, and they can be determined by fitting the relation of εn-γ, which is obtained by test.
From Eq. (5), one can further get
 (7)
(7)
For convenience, from Eq. (7), one can get
 (8)
(8)
According to Eq. (3), one can get
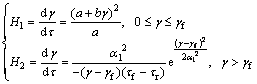 (9)
(9)
Mathematically,  . From Eq. (2) and Eqs. (8)-(9), parameter B can be found:
. From Eq. (2) and Eqs. (8)-(9), parameter B can be found:
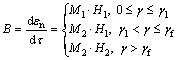 (10)
(10)
3.3 3D interface constitutive relations
For thin layer element, as shown in Fig. 12, according the 2D constitutive relation, the 3D stiffness matrix of the model is deduced under the following premises: 1) Neglecting cross impact of τyx and τyz; 2) Assuming that the shear stress τyx and τyz have the same stress-strain relations along the each shear direction.

Fig. 12 Schematic diagram of 3D interface element
The 3D constitutive relation is then expressed as
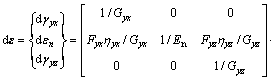
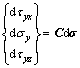 (11)
(11)
where En is determined by  . Gyx and Gyz are the shear moduli along the X axis and Z axis, respectively.
. Gyx and Gyz are the shear moduli along the X axis and Z axis, respectively.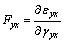 ,
,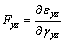 . εyx and εyz refer to
. εyx and εyz refer to
the components of the normal strain on the XZ plane due to the shear along the X axis and Z axis, respectively. After summarization of flexibility matrix, Eq. (11) can be rewritten as
 (12)
(12)
where C is flexibility matrix, and parameter L can be determined by using Ref. [34]:
 (13)
(13)
where
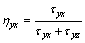


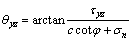
From Eq. (3) and Eq. (5), one can get
 (14)
(14)
 (15)
(15)
 (16)
(16)
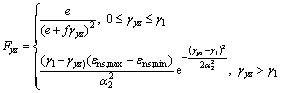 (17)
(17)
Then, the strain components can be denoted as
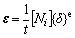 (18)
(18)
where Ni is shape function (i=1, 2, 3, 4, 5, 6, 7, 8), {δ}e is the nodal displacement. Ni can be determined by
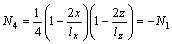

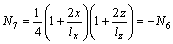

Further, stress can be expressed as
 (19)
(19)
 (20)
(20)
4 Finite element verification and discussion
A physical model test of cut-off wall was carried out in this work. To verify the presented constitutive model for the thin-layer type element, three-dimensional (3D) finite element method (FEM) was used to simulate this cut-off wall model test, and the FEM prediction is compared with the model test data.
The sketch of the indoor cut-off wall model test is shown in Fig. 13, and the 3D mesh of FEM is shown in Fig. 14. The size of the model is 80 cm×60 cm×120 cm. The dimension of the cut-off wall is 40 cm× 5 cm× 65 cm. In the model test, the mixed soil slurry is set up between concrete cut-off wall and a coarse-grained soil, and the interface is just believed to be the same as that tested in Section 2.
The concrete of cut-off wall is simulated by linear elastic model, the elastic modulus is 30 GPa, Poisson ratio is 0.18 and the density is 2.4 g/cm3. DUNCAN-ZHANG model is employed for the coarse-grained soil and clay around the cut-off wall of the model (Fig. 13(a)), and the parameters are listed in Table 2.
For comparison, Goodman model and the presented model are used to simulate the interface between soil and concrete, and parameters of Goodman model and presented model are shown in Table 3 and Table 4, respectively.
It should be mentioned that the parameters in Table 2 and 3 are determined by tests conducted by WANG, and those in Table 4 are determined by using test in Section 2.
For the concrete structure buried in soil, the stress of concrete is often difficult to give good prediction. This is mainly due to the simulating precision of the interface. In this section, therefore, the stress of cut-off wall is analyzed by comparing the predictions to the test data measured, as shown in Fig. 15.
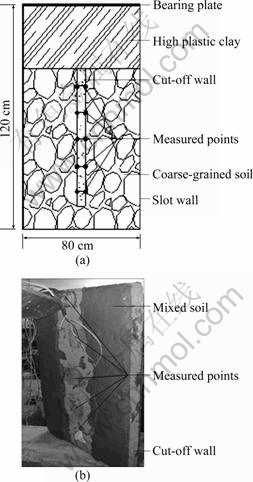
Fig. 13 Sketch maps of model test: (a) Schematic diagram of section; (b) Cut-off wall with mixed soil slurry

Fig. 14 3D FEM mesh of indoor cut-off wall test
Table 2 Parameters of main materials in finite element calculation

Table 3 Parameters of Goodman model in calculation

Table 4 Fitting values of parameters of new model for 3D FEM simulation

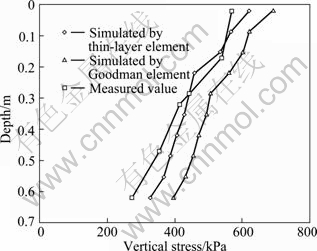
Fig. 15 Vertical stress of cut-off wall at different depth
From Fig. 15, it is seen that the predictions by the presented model agree well with the measured data of the model of cut-off wall, and the error is less than 10%. Nevertheless, the stresses of the cut-off wall predicted by Goodman interface model are much larger than the measured values, especially at the bottom of the wall, and the deviation is about 45%. In addition, at the top of wall, the error also reaches 30%. The presented interface model can reasonably reflect the behavior of the interface.
5 Conclusions
1) Existence of slurry and its composition exert much influence on mechanical behavior of the interface. The mechanical response of the interface varies with the different slurry.
2) The relation curve between shear stress and shear strain appears stress-strain softening and dilatancy with mixed soil slurry. The position of the peak strength is related to the normal stress.
3) The PFC simulation reveals that the disturbed height of the sample is related to the maximum particle diameter of the soil, and the normal stress and roughness of the interface. The disturbance could be neglected if the height of the interface exceeds a certain value. In the tests, the disturbed height is around 18 cm, so the thickness of the interface can be regarded as 18 cm.
4) A 2D constitutive model for thin layer element of interface is built based on the generalized potential theory. Plastic state equations are determined by fitting hyperbolic function and resembling normal function. Finally, model parameters are determined using simple shear test, and the model is extended to the case of 3D stress space.
5) An indoor cut-off wall model test is carried out, and 3D FEM is used to simulate the model test. The new model is apparently superior to Goodman model in aspect of the stress of the wall, and verifies the reasonability and applicability of the model.
References
[1] CLOUGH G W, DUNCAN J M. Finite element analysis of retaining wall behavior [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1971, 97 (SM12): 1657-1673.
[2] BRANDT J R T. Behavior of soil concrete interfaces [D]. Edmonton, Canada: University of Alberta, 1985: 72-95.
[3] KISHIDA H, UESUGI M. Tests of the interface between sand and steel in the simple shear apparatus [J]. Geotechnique, 1987, 37(1): 45-52.
[4] GENS A, CAROL I, ALONSO E E. An interface element formulation for the analysis of soil-reinforcement interaction [J]. Computers and Geotechnics, 1988, 7(1): 133-151.
[5] ZHANG Ga, ZHANG Jian-min. Experimental study on monotonic behavior of soil-structure interface with slurry [J]. Rock and Soil Mechanics, 2005, 26(9): 1 374-1 378. (in Chinese)
[6] FROST J D, DEJONG J T, RECALDE M. Shear failure behavior of granular-continuum interfaces [J]. Engineering Fracture Mechanics, 2002, 69(17): 2029-2048.
[7] HU Li-ming, PU Jia-liu. Testing and modeling of soil-structure interface [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(8): 851-860.
[8] SAID I, GENNARO D V, FRANK R. Axisymmetric finite element analysis of pile loading test [J]. Computers and Geotechnics, 2009, 36(1/2): 6-19.
[9] DOVE J E, JARRETT J B. Behavior of dilative sand interface in a Geotribology framework [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(1): 25-37.
[10] ZEGHAL M, Tuncer B E. Soil structure interaction analysis: Modeling the interface [J]. Canadian Geotechnical Journal, 2002, 39: 620-628.
[11] DEJONG J T, WESTGATE Z J. Role of over consolidation on sand-geomembrane interface response and material damage evolution [J]. Geotxtile sand Geomembranes, 2005, 23(6): 486-512.
[12] MILLER G A, HAMID T B. Interface Direct shear testing of unsaturated soil [J]. Geotechnical Testing Journal, 2007, 30(3): 182-191.
[13] TUNCER B E, PETER J B, AARON J S. Soil-structure interface shear transfer behavior [J]. Geomechanics ASCE, 2005: 528-543.
[14] SHAKIR R R. Experimental study and numerical constitutive modeling of soil-concrete interaction [D]. Nanjing: Hohai University, Civil Engineering Department, 2009: 110-116.
[15] BOULON M, PLYTAS C. Soil structure directionally dependent interface constitutive equations-application to the prediction of shaft friction along plies [C]// Proceedings of the Second International Symposium on Numerical Models in Geo-mechanics. Ghent, Belgium: 1986: 43-54.
[16] DESAI C S, PRADHAN S K. Cyclic testing and constitutive modeling of saturated sand-concrete interfaces using the disturbed state concept [J]. International Journal of Geomechanics, 2005, 5(4): 286-294.
[17] MORTARA G., BOULON M, GHIONNA V N. A 2D constitutive model for cyclic interface behavior [J]. Int J Numer Anal Meth Geomech, 2002, 26(11): 1071-1096.
[18] GENNARO V, FRANK R. Elasto-plastic analysis of the international behavior between granular media and structure [J]. Computers and Geotechnics, 2002, 29: 547-572.
[19] CABALLERO A, WILLAM K J, CAROL I. Consistent tangent formulation for 3D interface modeling of cracking/fracture in quasi-brittle materials [J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(33-40): 2804-2822.
[20] PASTER M, ZIENKIEWICZ O C, CHAN A H C. Generalized plasticity and the modeling of soil behavior [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1990, 14(3): 151-190.
[21] YANG Guang-hua. A new strain space elastopalstic constitutive model for soil [C]// Proceedings of Second International Conference on Soft Soil Engineering. Nanjing: Hohai University Press, 1996: 1-8.
[22] YIN Zong-ze, ZHU Hong, XU Guo-hua. Numerical simulation of the deformation in the interface between soil and structure material [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(3): 14-22. (in Chinese)
[23] ZHANG Zhi-jun, RAO Xi-bao, WANG Zhi-jun, DING Hong-shun. Experimental study on influence of slurry thickness on mechanical behavior of interface between gravel and concrete [J]. Rock and Soil Mechanics, 2008, 29(9): 2433-2438. (in Chinese)
[24] ZHANG Ga, ZHANG Jian-min. Three-dimensional model of interface between structure and coarse grained soil [J]. Rock and Soil Mechanics, 2007, 28(2): 288-292. (in Chinese)
[25] ZHANG Miao-zhong, ZHANG Guang-xing, WU Qing-yong, XIN Gong-feng. Studies on characteristics of mudcake and soil between bored plies [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 695-699. (in Chinese)
[26] PENG Kai, ZHU Zhu-gao, ZHANG Dan, WU Xiao-yu. Study of mechanical behaviors of interface between coarse-grained soil and concrete by simple shear tests [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1983-1990. (in Chinese)
[27] THORNTON C, ZHANG L. A DEM comparison of different shear testing devices [C]// 4th International Conference on Micromechanics of Granular Media. Rotterdam, The Netherlands: 2001: 183-189.
[28] POTYONDY D O, CUNDALL P A. A bonded-particle model for rock [J]. International Journal of Rock Mechanics Mining Sciences, 2004, 41: 1329-1364.
[29] SEGUEL O, HORN R. Mechanical behavior of a volcanic ash soil under static and dynamic loading [J]. Soil and Tillage Research, 2005, 82(1): 109-116.
[30] YANG Xiao-li, HUANG Fu. Collapse mechanism of shallow tunnel based on nonlinear Hoek-Brown failure criterion [J]. Tunnelling and Underground Space Technology, 2011, 26(6): 686-691.
[31] YANG Xiao-li, WANG Jin-min. Ground movement prediction for tunnels using simplified procedure [J]. Tunnelling and Underground Space Technology, 2011, 26(3): 462-471.
[32] YANG Xiao-li. Seismic passive pressures of earth structures by nonlinear optimization [J]. Archive of Applied Mechanics, 2011, 81(9): 1195-1202.
[33] YANG Xiao-li, HUANG Fu, WANG Jin-min. Modified image analytical solutions for ground displacement using the nonuniform convergence model [J]. Journal of Central South University of Technology, 2011, 18(3): 859-865.
[34] ZHOU Ai-zhao, LU Ting-hao. Elasto-plastic constitutive model of soil-structure interface in consideration of strain softening and dilation [J]. Acta Mechanics Solida Sinica, 2009, 22(2): 171-179.
(Edited by YANG Bing)
Foundation item: Project(20110094110002) supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China; Project(200801014) supported by the Ministry of Water Resources of China; Project(50825901) supported by the National Natural Science Foundation of China
Received date: 2011-05-03; Accepted date: 2011-11-30
Corresponding author: PENG Kai, PhD; Tel: +86-15974294545; E-mail: pengkai@hhu.edu.cn