Trans. Nonferrous Met. Soc. China 25(2015) 582-589
Self-heating tendency evaluation of sulfide ores based on nonlinear multi-parameters fusion
Wei PAN 1, 2, Chao WU 2, Zi-jun LI 2, Yue-ping YANG 3
1. Key Laboratory of Mine Thermo-motive Disaster and Prevention of Ministry of Education, Liaoning Technical University, Fuxin 123000, China;
2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
3. School of Nuclear Resources Engineering, University of South China, Hengyang 421001, China
Received 4 March 2014; accepted 10 September 2014
Abstract: In order to reveal the nonlinear dynamics characteristics of unsteady self-heating process of sulfide ores, nine different kinds of sulfide ore samples from a pyrite mine in China were taken as experimental materials and their self-heating characteristics were measured in laboratory. Furthermore, the measured temperature was studied by integrating wavelet transform, nonlinear characteristic parameters extraction and fuzzy comprehensive evaluation. The results indicate that only the ore samples 1, 2, 6 and 9 have obvious self-heating phenomenon, and their self-heating initiative temperatures are 220 °C, 239 °C, 220 °C and 220 °C, respectively, which means that they are difficult to produce self-heating under normal mining conditions. The correlation dimension of self-heating process is fraction and the maximum Lyapunov exponent is positive, which means that it is feasible to study the self-heating process based on chaotic dynamics theory. The nonlinearities of self-heating process of these four samples (ore samples 1, 2, 6 and 9) are 0.8227, 0.7521, 0.9401 and 0.8827 respectively and the order of the samples according to these results is: sample 6, sample 9, sample 1, sample 2, which is consistent with the measured results of self-heating characteristics. Therefore, the nonlinearity method can be used to evaluate the self-heating tendency of sulfide ores, and it is an effective verification of the reliability of measured results.
Key words: sulfide ores; self-heating process; nonlinear characteristic parameter; nonlinearity; self-heating tendency
1 Introduction
Spontaneous combustion of sulfide ores is a conversion of the chemical energy to heat due to oxidation [1-3]. If the reaction heat doesn’t dissipate entirely, sulfide ores will be heated and release more and more heat, which is a positive feedback. When the temperature of sulfide ores reaches the ignition temperature, spontaneous combustion will take place. It is well known that spontaneous combustion of sulfide ores is one of the most serious disasters in sulfide deposits mining [4-6]. According to statistics of spontaneous combustion, it has occurred in more than ten mines in China since 1949, such as Wushan Copper Mine, Xiangshan Pyrite Mine and Dongguashan Copper Mine [7]. Spontaneous fires of sulfide ores not only generate massive toxic gas and heat to worsen the work environment, but also bring about large economic losses even loss of human life. For the rapid decrease of surface mineral resources, deep mining has become a trend and its high temperature can cause spontaneous combustion more easily. Therefore, researches on the oxidation mechanism, prevention and control technology of spontaneous combustion are a premise to ensure safe and efficient mining for high-sulfur mines.
In recent years, evaluation for spontaneous combustion tendency of sulfide ores has attracted attention of many researchers and some new evaluation methods have been proposed, such as apparent activation energy method [8], matter-element model [9], evaluation model based on entropy and set pair analysis theory [10], Fisher discriminant analysis method [11] and uncertainty measurement model [12]. To evaluate the spontaneous combustion tendency of sulfide ores synthetically, self-heating initiative temperature, which is measured by carrying out self-heating characteristics experiment, is commonly used as an index. As the self-heating of sulfide ores is a nonlinear multi-factor coupling evolution process, research on the unsteady self-heating process by means of nonlinear dynamics theory is worthy of further study. Currently, there are very scarce researches on nonlinear characteristics of self-heating process.
In this work, nine kinds of typical sulfide ore samples from a pyrite mine in China were taken as experimental materials and their self-heating characteristics were measured with precision instruments in laboratory. Combined with wavelet transform, nonlinear characteristic parameters extraction and fuzzy comprehensive evaluation, the nonlinearity of ore samples self-heating process, which is the characterization of complexity for self-heating process, was calculated. Moreover, self-heating tendency evaluation method of sulfide ores based on nonlinear multi-parameters fusion was proposed.
2 Experimental
2.1 Ore samples collection and analysis
Sulfide ore samples were collected from a pyrite mine in China with the sampling method of multi-point sampling, and nine types of representative samples were taken as experimental materials. As an example, the chemical composition of the ore sample 1 is listed in Table 1.
Table 1 Chemical composition of ore sample 1 (mass fraction, %)
The metallic mineral of the ore sample 1 is pyrite with two-stage mineralization. The largest size of early-stage pyrite particles is about 5 mm, and their average size is about 2 mm. They are fragmented as a result of the stress action. Unlike the early-stage pyrite particles, the late-stage pyrite particles are fine-grained aggregates with the average size of about 5 μm. The micrograph of the ore sample 1 is shown in Fig. 1.
2.2 Experimental method
In the experiment, the particle diameter of ore samples was ground to less than 0.2 mm. Each sample with mass of about 100 g and moisture content of about 5% was installed into the reactor in the automatic heating incubator to measure its self-heating characteristics owing to the weak oxidation of sulfide ores at normal temperature. The initial temperature was set between 40 and 50 °C and one single heating extent was about 10 °C. After the temperature of automatic heating incubator reached the setting temperature, it was kept isothermal for about 30 min. During the experiment process, the maximum temperature of automatic heating incubator was not higher than 250 °C. The experimental devices are shown in Fig. 2.
Fig. 1 Micrograph of ore sample 1
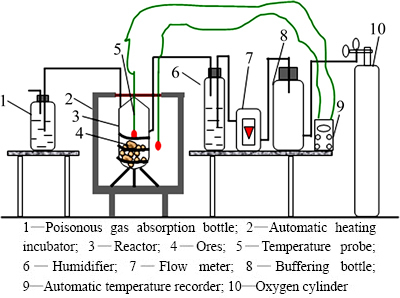
Fig. 2 Schematic diagram of experimental apparatus
3 Experimental results
By analyzing the self-heating characteristic curves of ore samples, it can be found that only the ore samples 1, 2, 6 and 9 have obvious self-heating phenomenon, and their self-heating initiative temperatures are 220 °C, 239 °C, 220 °C and 220 °C, respectively, which means that they are difficult to produce self-heating under normal mining conditions. Figure 3 displays the self-heating characteristic curve of the ore sample 1. It shows that the obvious self-heating period lies between 1200 and 1230 min and the maximum self-heating extent is 5 °C.
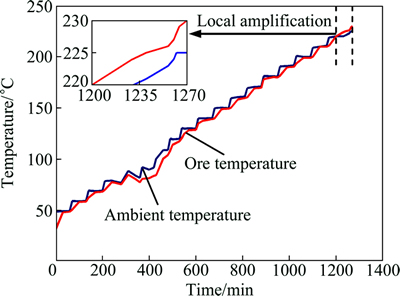
Fig. 3 Self-heating characteristic curve of ore sample 1
4 Preprocessing of measured temperature series
Temperature variations of ore samples are caused by the comprehensive effect of automatic heating incubator and exothermic oxidation of ore samples, and the former plays a dominant role. Hence, it is necessary to separate self-heating information from the measured temperature series. Then, the temperature series were processed by wavelet decomposition and reconstruction [13]. The low frequency components of the series (large scale approximation parts) reflect the effect of gradient temperature-elevating with automatic heating incubator, and high frequency components (details) contain the complicated self-heating information of ore samples.
Owing to the limited measured data, the temperature series of the four samples (ore samples 1, 2, 6 and 9) were extended with the cubic spline interpolation method, and the length of the expanded series was 301. For temperature increments could show the pre- and post-temperature variations more intuitively, they were selected as the research objects.
The temperature increment series were transformed with the same wavelet function of bior3.1 based on the results of wavelet optimization. The characteristic values of corresponding series are listed in Table 2, which indicate that the temperature increment series are well correlated for all the autocorrelation coefficients, greater than 0.86, and the skewness coefficients have a significant difference.
For these four kinds of ore samples, their temperature increment series were decomposed with wavelet bior3.1, and then the first layer of high frequency coefficients were reconstructed. Finally, the reconstructed high frequency series were normalized as the research series.
Wavelet reconstruction for temperature increment series of the ore sample 1 is shown in Fig. 4. The trend of low frequency reconstructed series, which reflects the effect of gradient temperature-elevating, is consistent with that of the original sequence in general. High frequency reconstructed series have more complicated detailed change, which can amplify the tiny distinction of self-heating process effectively.
5 Extraction of nonlinear multi-parameters
According to the definitions of approximate entropy, correlation dimension and the maximum Lyapunov exponent, each of them can be adopted to characterize the chaotic features from different aspects. Approximate entropy mainly reflects the disorder degree of the time series. Correlation dimension is a measure of the complexity for chaotic series. Maximum Lyapunov exponent is an estimation of predictability for chaotic series. Therefore, these three kinds of nonlinear characteristic parameters were extracted from research series as evaluation indexes for self-heating tendency.
Table 2 Characteristic values for corresponding series of ore samples
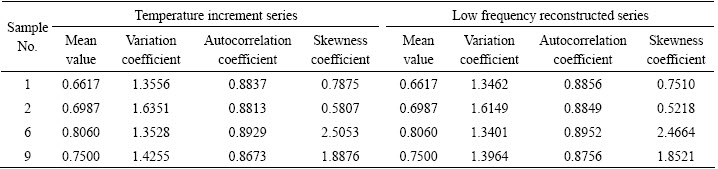
Fig. 4 Wavelet reconstruction for temperature increment series of ore sample 1
5.1 Extraction of approximate entropy
For a given N-point research series {x(i), i=1, …, N}, approximate entropy can be obtained by the following steps (m is the dimension, and r is the threshold value) [14]:
1) Compose the m-dimensional vector X(i) as follows:
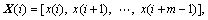
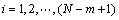(1)
2) For every i value, calculate the distance between X(i) and X(j), namely
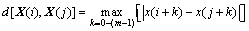(2)
3) Given the threshold value r (r>0), for each i value, count the number of d[X(i), X(j)]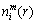
) and calculate the ratio of 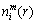to the total number of vectors (denoted as 
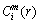), so
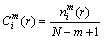(3)
4) Calculate the logarithm of 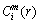and its average value, denoted as 
, namely
(4)
5) For m + 1, repeat steps 1–4 to obtain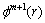 
. The approximate entropy value is as follows:
(5)
Usually, m=2 and r=kσ (k is empirical coefficient, k=0.1-0.2; σ is standard deviation of research series) are used to calculate the approximate entropy.
In this work, empirical coefficient was determined according to the variation extent of approximate entropy with different k values, which can be expressed as
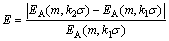(6)
For all the ore samples, when the average E takes on minimum value, the corresponding k value is optimal.
Figure 5 denotes the variation of approximate entropy with different values of k. With the increase of k, approximate entropy for research series of the ore sample 9 gradually increases, while the others decrease, as shown in Fig. 5. When k=0.15, the average E takes a minimum value of 0.66%. Correspondingly, approximate entropies of the ore samples 1, 2, 6 and 9 are 0.6309, 0.6229, 0.5759 and 0.6251, respectively.
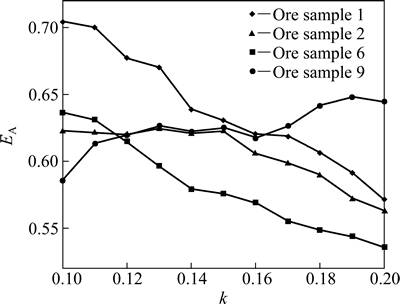
Fig. 5 EA-k curves for ore samples
5.2 Extraction of correlation dimension
Correlation dimension can be calculated by the following steps based on the GP algorithm [15]:
1) For the m-dimensional reconstructed phase space, define the correlation integral as
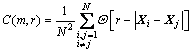(7)
where N is the number of phase point, r is hypersphere radius, │Xi-Xj│is the euclidean distance between the phase point Xi and Xj, and Θ is called Heaviside function.
2) Adjust the value of r in a certain range to meet
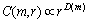(8)
where D(m) is an estimation of correlation dimension.
3) When the embedding dimension m is equal to the saturated embedding dimension mc, D(m) will be stable and the stable value is correlation dimension D2.
In actual calculation of D2, the optional delay time τ was obtained using the improved auto-correlation function method [16] firstly, and then D2 was extracted in reconstructed phase space.
ln C(m,r)-ln r curves for research series of the ore sample 1 are depicted in Fig. 6(a), which indicate that ln C(m,r) increases at first and then tends to be stable with ln r. The calculated results are D2=1.4503 and mc=6, as shown in Fig. 6(b).
The calculated results D2 for all the samples are listed in Table 3.
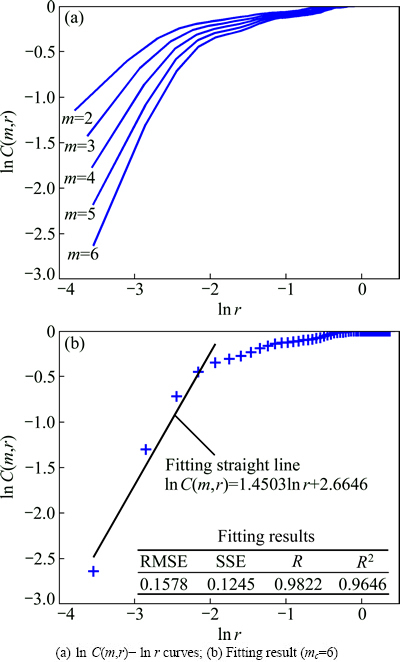
Fig. 6 D2 calculation process for ore sample 1
Table 3 Calculated results D2 for ore samples
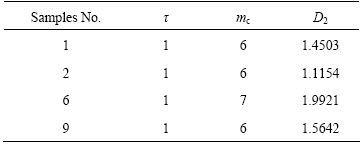
5.3 Extraction of maximum Lyapunov exponent
Maximum Lyapunov exponent can be calculated by the following steps by means of small data sets [17].
1) In the m-dimensional reconstructed phase space, search the nearest neighbor point Xjj of the reference point Xj and keep temporal separation:
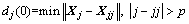(9)
where dj(0) is the initial distance between the phase point Xj and its nearest neighbor point Xjj and p is the mean period of research series.
2) To each point Xj, calculate the distance dj(i):
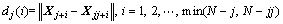(10)
3) For general j, calculate the average value of y(i):
(11)
where q is the number of all non-zero dj(i).
4) Select the linear region of y(i)-i curves and make the regression line using the least square method. The slope of the line is the maximum Lyapunov exponent λmax.
For the ore sample 1, the mean period of research series was calculated with the value of 3 based on FFT method. The phase space was reconstructed with m=6 and τ=1, and then the maximum Lyapunov exponent (λmax=0.0037) was calculated following the above step. Figure 7 shows the λmax result for the ore sample 1.
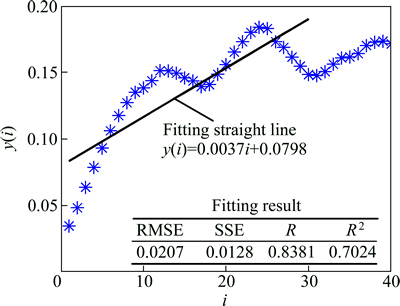
Fig. 7 λmax result for ore sample 1
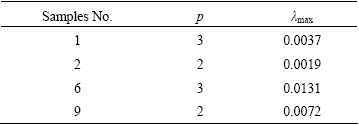
Table 4 lists the calculated results of λmax for all samples. In conjunction with Table 3, it is known that for each sample, the correlation dimension of self-heating process is fraction and the maximum Lyapunov exponent is positive, which means that self-heating of sulfide ores is a chaotic evolution process. As a result, it is feasible to study the self-heating process based on chaotic dynamics theory.
Table 4 Calculated results λmax for ore samples
6 Self-heating tendency evaluation by means of nonlinearity
The maximum Lyapunov exponent can be used to characterize the nonlinear degree of self-heating process, but it needs high precision long series to obtain the precise value and is sensitive to noise. So it is limited in actual use. To compensate for this deficiency, approximate entropy, correlation dimension and the maximum Lyapunov exponent were fused, and the integration value was defined as nonlinearity to be used to measure the degree of irregularity and complexity for the self-heating process from dynamic aspect.
According to the conception of nonlinearity, define the nonlinearity vector of self-heating process as U=(u1, u2, u3), where u1, u2 and u3 are approximate entropy, correlation dimension and the maximum Lyapunov exponent, respectively. To eliminate their physical and geometric meaning and difference of order of magnitude, ui (i=1, 2, 3) need to be normalized, namely ui∈U, U=(0, 1). Meanwhile, define the evaluation set as V=(v1, v2, v3, v4), where v1, v2, v3 and v4 are corresponding to the ore samples 1, 2, 6 and 9.
Given the factors set U and evaluation set V, α: U→V is univariate evaluation function, so f(α(u1), α(u2), α(u3)) is the comprehensive evaluation of U [18]. Generally, comprehensive evaluation function involves two weight vectors, namely normalized weight vector and regularization weight vector.
In this work, the normalized weight vector was obtained with the value of (0.37, 0.31, 0.32), and the univariate evaluation matrix R=(rij)3×4 was established as
(12)
Four kinds of evaluation functions were utilized to assess the nonlinear intensity of self-heating process.
When using the weighted average model, namely,
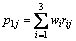(13)
where wi is the weight vector elements and rij is the scalar of normalized factors.
The evaluation value is P1=(p11, p12, p13, p14)= (0.6861, 0.5853, 0.9677, 0.7859).
When using the geometric mean model, namely,
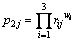(14)
The evaluation value is P2=(p21, p22, p23, p24)= (0.6047, 0.4483, 0.9668, 0.7634).
When using the univariate decision model, namely,
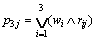(15)
The evaluation value is P3=(p31, p32, p33, p34)= (1, 0.9873, 0.9128, 0.9908).
When using the main factors prominent model, namely,
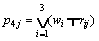(16)
The evaluation value is P4=(p41, p42, p43, p44)= (1, 0.9873, 0.9128, 0.9908).
The above four kinds of evaluation values were taken as the initial evaluations, and then all of the initial evaluations were further evaluated. The final evaluation matrix Rp was constructed based on the initial evaluation Pi (i=1, 2, 3, 4), namely,
Rp=(P1, P2, P3, P4)T (17)
According to the weighted average function, the formula of nonlinearity can be written as
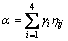(18)
where α is the nonlinearity, γi is the weight coefficient with the value of 0.25 and η1-η4 are the column vectors of Rp.
Table 5 Sort of self-heating tendency and α of ore samples
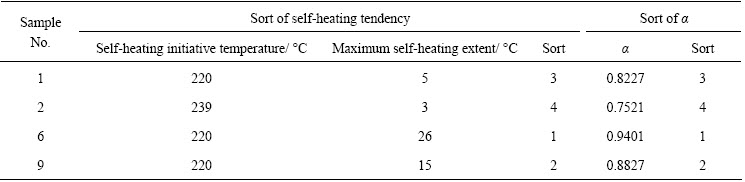
The sort of self-heating tendency and nonlinearity of ore samples are listed in Table 5. From Table 5, it is found that the sort of nonlinearity is consistent with that of the self-heating tendency. Thus, the self-heating tendency of sulfide ores can be evaluated by means of nonlinearity method.
The main purpose for the self-heating characteristics experiment of sulfide ores is to reveal the relationship between self-heating effects and the ambient temperature of automatic heating incubator and determine the lowest ambient temperature that induces rapid oxidation of sulfide ores. Theoretically, as the ambient temperature rises, the oxidation heat liberation increases and meanwhile the condition of heat dissipation deteriorates. When the ambient temperature reaches the critical value, the amount of heat liberation will be greater than that of heat dissipation, and obvious self-heating will appear in the ores due to the effect of heat accumulation simultaneously. But during the actual measurement process, temperature of ore samples often does not exceed the ambient temperature owing to the low heat liberation and other restrictive factors. Hence, it is difficult to determine the self-heating initiative temperature of ore samples accurately. In addition, the difference of temperature elevation program has a certain impact on the measured results of self-heating characteristics. Thus, the reliability of the evaluation results based on only the measured values in laboratory needs to be further verified.
The nonlinearity proposed in this work was extracted from all the measured temperature data by integration of multiple nonlinear characteristic parameters, and the effect of automatic heating incubator was eliminated with the wavelet technology during the calculation process. Since the self-heating of sulfide ores is a typical nonlinear evolution process, it is more objective to evaluate self-heating tendency with the nonlinearity method. The practical application indicates that the evaluation results are of high distinction and can be used to verify the reliability of the measured results.
7 Conclusions
1) The measured results of self-heating characteristics indicate that only the ore samples 1, 2, 6 and 9 have obvious self-heating phenomenon, and their self-heating initiative temperatures are 220 °C, 239 °C, 220 °C and 220 °C, respectively. Namely, sulfide ores of the pyrite mine are difficult to produce self-heating under normal mining conditions.
2) The extracted correlation dimension is fraction and the extracted maximum Lyapunov exponent is positive, which means that self-heating of sulfide ores is a chaotic evolution process. So, it is feasible to study the self-heating process based on chaotic dynamics theory.
3) The self-heating process nonlinearity of these four samples (ore samples 1, 2, 6 and 9) are 0.8227, 0.7521, 0.9401 and 0.8827, respectively and the order of the samples according to these results is: sample 6, sample 9, sample 1, sample 2, which is consistent with the measured results of self-heating characteristics. Therefore, self-heating tendency of sulfide ores can be evaluated by using the nonlinearity method, which is an effective verification of the reliability of measured results.
References
[1] NINTEMAN D J. Spontaneous oxidation and combustion of sulfide ores in underground mines [R]. USA: Bureau of Mines, 1978: 1-40.
[2] WU C, LI Z J. A simple method for predicting the spontaneous combustion potential of sulfide ores at ambient temperature [J]. Transactions of the Institutions of Mining and Metallurgy, Section A, 2005, 114(2): 125-128.
[3] YANG F Q, WU C, LI Z J. Investigation of the propensity of sulfide concentrates to spontaneous combustion in storage [J]. Journal of Loss Prevention in the Process Industries, 2011, 24: 131-137.
[4] LIU Hui, WU Chao, SHI Ying. Locating method of fire source for spontaneous combustion of sulfide ores [J]. Journal of Central South University of Technology, 2011, 18(4): 1034-1040.
[5] PAN W, LIAO J, WU C, LI Z J. Numerical simulation of self-heating and its influence factors of sulfide ore heap [C]//Proceedings of International Symposium on Rock Mechanics and Mine Dynamic Disaster Prevention. Beijing: China Coal Industry Publishing House, 2013: 221-227.
[6] LI Zi-jun, SHI Dong-ping, WU Chao, WANG Xiao-lei. Infrared thermography for prediction of spontaneous combustion of sulfide ores [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(12): 3095-3102.
[7] WU Chao, MENG Ting-rang. Theory and technology for control of the mine spontaneous combustion of sulfide ores [M]. Beijing: Metallurgical Industry Press, 1995: 3-15. (in Chinese)
[8] YANG Fu-qiang, WU Chao, CUI Yan, LU Guang. Apparent activation energy for spontaneous combustion of sulfide concentrates in storage yard [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(2): 395-401.
[9] YANG Fu-qiang, WU Chao, LI Zi-jun. Matter-element model and its application to comprehensive determination on spontaneous combustion tendency of sulfide ores [J]. Journal of Central South University: Science and Technology, 2011, 42(11): 3459-3464. (in Chinese)
[10] XIE Zheng-wen, WU Chao, LI Zi-jun, YANG Fu-qiang. Evaluation on spontaneous combustion tendency of sulfide ores based on entropy and set pair analysis theory [J]. Journal of Central South University: Science and Technology, 2012, 43(15): 1858-1863. (in Chinese)
[11] HU Han-hua, LIU Zheng, LI Zi-jun, CUI Tian-tian. Fisher discriminant analysis to the classification of spontaneous combustion tendency grade of sulphide ores [J]. Journal of China Coal Society, 2010, 35(10): 1674-1679. (in Chinese)
[12] YANG Fu-qiang, WU Chao, LI Zi-jun. Application of uncertainty measurement model in risk evaluation on spontaneous combustion of sulfur concentrate in storehouse [J]. Journal of China Coal Society, 2010, 35(2): 264-268. (in Chinese)
[13] SANG Yan-fang, WANG Dong. Wavelets selection method in hydrologic series wavelet analysis [J]. Journal of Hydraulic Engineering, 2008, 39(3): 295-300. (in Chinese)
[14] PINCUS S M. Approximate entropy as a measure of system complexity [J]. Proceeding of the National Academy Sciences USA, 1991, 88(6): 2297-2301.
[15] GRASSBERGER P, PROCACCIA I. Dimension and entropy of strange attractors from a fluctuating dynamic approach [J]. Physica, 1984, 13: 34-54.
[16] YU Da-peng, ZHAO De-you, WANG Yu. Chaotic dynamics of propeller singing [J]. Acta Acustica, 2010, 35(5): 530-538. (in Chinese)
[17] MICHAEL T R, JAMES J C, CARLO J D L. A practical method for calculating largest lyapunov exponents from small data sets [J]. Phaysical D, 1993, 65(1/2): 117-134.
[18] WANG Bing-cheng, REN Zhao-hui, WEN Bangchun. Fault diagnoses method of rotating machines based on nonlinear multi-parameters [J]. Journal of Mechanical Engineering, 2012, 48(5): 63-69. (in Chinese).
基于非线性多参数融合的硫化矿石自热倾向性评价
潘 伟1, 2，吴 超2，李孜军2，杨月平3
1. 辽宁工程技术大学 矿山热动力灾害与防治教育部重点实验室，阜新123000；
2. 中南大学 资源与安全工程学院，长沙410083；
3. 南华大学 核资源工程学院，衡阳421001
摘 要：为揭示硫化矿石非稳态自热过程的非线性动力学特征，以从某硫铁矿采集的9种硫化矿石样品为实验材料，开展室内矿石自热特性实验。采用集成小波变换、非线性特征参数提取和模糊综合评判等方法对实测温度数据进行研究。结果表明：仅矿样1、2、6和9出现明显自热，自热起始温度分别为220、239、220和220 °C，在正常采矿条件下矿石不易产生自热；矿样自热过程的关联维数均为分数，最大Lyapunov指数均大于0，验证了基于混沌动力学理论研究自热过程的可行性；矿样自热过程的非线性度分别为0.8227、0.7521、0.9401和0.8827，排序依次为矿样6、矿样9、矿样1、矿样2，与自热特性测定结果一致。因此，可采用非线性度方法来评价硫化矿石自热倾向性，该方法可对实测结果的可靠性进行有效验证。
关键词：硫化矿石；自热过程；非线性特征参数；非线性度；自热倾向性
(Edited by Yun-bin HE)
Foundation item: Project (51304238) supported by the National Natural Science Foundation of China; Project (JSK200206) supported by the Foundation of Key Laboratory of Mine Thermo-motive Disaster and Prevention, Ministry of Education, China
Corresponding author: Wei PAN; Tel: +86-13875801845; E-mail: panwei2012@csu.edu.cn
DOI: 10.1016/S1003-6326(15)63640-8
