基于单轴各向异性完全匹配层边界条件的
ADI-FDTD三维GPR全波场正演
冯德山，谢源
(中南大学 地球科学与信息物理学院，湖南 长沙，410083)
摘要：基于交替方向隐式差分(ADI-FDTD)法突破了CFL稳定性条件的约束，具有无条件稳定性的特点，而单轴各向异性完全匹配层(UPML)边界条件具有宽频带吸收特性、不需要对电场和磁场进行分裂、迭代公式简单、便于编程的特点，提出基于UPML边界条件的ADI-FDTD三维探地雷达数值模拟算法；通过对三维Maxwell方程进行离散化，推导GPR波的ADI-FDTD及其UPML边界条件2个子时间步的迭代差分公式，以及计算步骤。开发ADI-FDTD三维模拟程序，并对三维复杂GPR模型进行正演模拟，分析该模型的剖面图、切片图及不同时刻6个分量的全波场快照。研究结果表明：由全波场快照可以了解雷达波形在空间中的传播过程及变化规律，有助于对雷达资料进行更可靠、更准确的解释；基于UPML边界条件的ADI-FDTD算法消除了截断边界处的强反射，能对三维复杂的GPR模型进行快速、高效模拟。
关键词：探地雷达；交替方向隐式有限差分法；单轴各向异性完全匹配层；正演
中图分类号：P631 文献标志码：A 文章编号：1672-7207(2011)08-2363-09
Three dimensional GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD
FENG De-shan, XIE Yuan
(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Abstract: Based on the fact that ADI-FDTD can break through the restriction of the CFL stability condition and its unlimited stable, however, UPML boundary condition has the characteristic of absorbing wide frequency and without the necessity for separating electric field from magnetic field, and its simple iterative formula is convenient for compiling program. The GPR numerical simulation arithmetic of ADI-FDTD was put forward based upon UPML boundary condition. Through the discretization of the three-dimension Maxwell equations, two sub-time step iterative finite difference formula of ADI-FDTD and UPML boundary condition of GPR wave were studied, and the compute steps were given separately. Based on this, the responding ADI-FDTD three-dimension simulation program was complied, the program to forward simulate the complex three-dimension GPR model was used, and fence diagram, slice map and the full wave snapshot of six components were obtained. The results show that the regulation of radar wave spreads and changes in the space to guide interpretation of radar data reliably and accurately. The ADI-FDTD algorithm based on the UPML boundary condition can eliminate the strong reflection of truncating boundaries and imitate GPR model’s reliability and accurately.
Key words: ground penetrating radar; alternating direction iterative finite difference time domain; uniaxial perfectly matched layer; forward simulation
探地雷达(Ground penetrating radar，GPR)数值模拟一直是该领域理论研究的热点。底青云等[1]应用有限元方法推导了含衰减项的雷达波方程，实现了管状体、弯曲界面等复杂形体的雷达波场仿真模拟；Liu等[2]利用傅里叶时域伪谱算法开展了雷达波传播规律和目标散射特性的研究；刘四新等[3]利用时域有限差分法(FDTD)并结合基于分裂场的Berenger PML边界条件实现了雷达波在有损耗介质中的模拟；肖明顺 等[4]研究FDTD算法中的单轴各向异性理想匹配层(UPML)边界条件；李静等[5]为了提高模拟精度，采用高阶时域有限差分法并结合UPML边界条件进行了探地雷达数值模拟；Szerbiak等[6]考虑到二维模拟不能提供多极化探测响应和探测目标体的形状、空间分布、延伸走向等详细信息，应用FDTD进行了探地雷达三维正演模拟。目前，GPR正演模拟主要针对以下2个问题：(1) GPR模拟对象由简化的理想介质向考虑吸收衰减的有耗色散媒质转变，GPR模型趋于复杂化、三维化；(2) GPR模拟手段日趋多样化，许多新方法也开始在GPR正演中得到应用。以FDTD方法为例，鉴于传统FDTD方法受Courant-Friedrich-Levy(CFL)稳定条件的约束，存在时间和空间步长的选取不能太大、计算效率较低问题[7]。近年来，人们相继提出和发展了一些融合其他技术的FDTD方法，其中比较成功的有：时域多分辨小波(Multi-resolution time domain，MRTD)[8]、伪谱时域差分(Pseudo-spectral time domain，PSTD)[9]和交替方向隐式时域差分方法 (Alternating Direction Implicit，ADI-FDTD)[10]等。Krumpholz等[11]结合小波技术提出的MRTD方法，时间约束条件要比CFL稳定性条件更为苛刻，可以说是“以时间换取空间”。Liu等[12]提出的PSTD方法本身有2个技术问题亟待解决：一是“点源效应”的Gibbs现象；二是空间的不连续性致使均匀空间的FFT算法出现较大的运算误差。而ADI-FDTD方法[13]将隐式差分格式的无条件稳定性和显式差分格式计算相对简单的优点融为一体，是一种无条件稳定的交替方向隐式时域有限差分法，它克服了常规FDTD法受CFL约束条件限制的缺点，可选取较大的时间步长，将传统的1个时间步分成了2个分时间步，这2个分时间步分别采用前向和后向差分，其误差互相弥补。2步复合的结果可以保证解是无条件稳定的，同时提高了计算效率。在此，本文作者利用无条件稳定的ADI-FDTD算法结合UPML边界条件进行GPR三维全波场数值模拟，大大降低了边界上的反射，提高了GPR模拟精度，除GPR模拟得到的三维切片图、剖视图之外，还得到了6个电场与磁场分量Ex，Ey，Ez，Hx，Hy和Hz在不同时刻的波场快照，通过对这些切片图、剖视图及波场快照进行分析，能更加直观、全面地了解雷达波在三维空间的传播特性，指导三维雷达探测技术的开展。
1 ADI-FDTD法差分公式
由电磁波传播理论[14]可知，GPR遵循的Maxwell方程的 6个偏微分方程可表示如下：
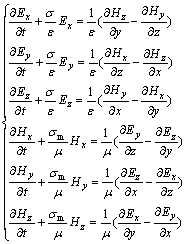(1)
式中：Ex，Ey和Ez分别为x，y和z方向电场强度；Hx，Hy和Hz分别为x，y和z方向磁场强度；ε为介电常数；μ为磁导率；σ为电导率；σm为导磁率。下面对6个偏微分方程分2个过程进行差分离散：在n→n+1/2步中，Maxwell旋度方程左边的时间偏微分项对x方向导数?Hz/?y的差分离散取隐式，对y方向导数?Hy/?z的差分离散取显式[14]；在n+1/2→n+1步中，对x方向导数的差分离散取显式，对y方向导数的差分离散取隐式。以n→n+1/2过程为例予以说明(n+1/2→n+1计算过程可类似得到)。
在n→n+1/2步中，Maxwell旋度方程左边的时间偏微分项采用中心差分格式，对z方向导数?Hz/?y的差分离散取隐式，对y方向导数?Hy/?z的差分离散取显式，Ex分量在n和n+1/2时刻均取值，则式(1)中各分量离散为：
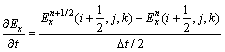
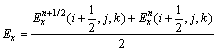
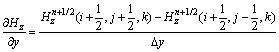
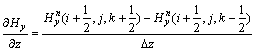
并定义：
，
，
，
。
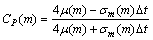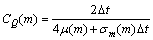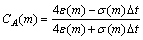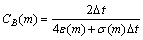若定义标号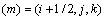
，则式(1)的差分格式为：
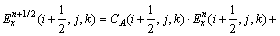
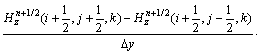
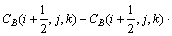
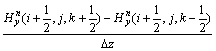(2)
在n→n+1/2步中，式(1)中的其他5个方程的差分格式可类似得到。分析差分方程式(2)的右端存在与左端同时间步的场分量，故不能像常规FDTD那样直接构成显式时间步推进计算，从逻辑上说，时间步进是无法完成的，称为隐式格式。为克服此困难，将
与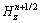
(i+1/2，j-1/2，k)参照式(2)类似推导，并把它代入式(2)中，得：
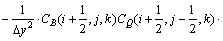
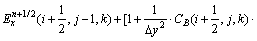
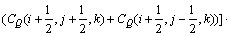
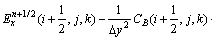
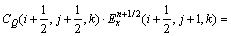
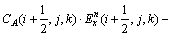
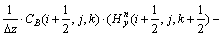
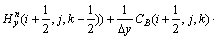
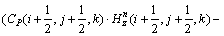
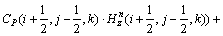
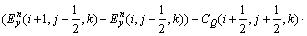
(3)
若令：
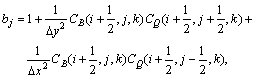
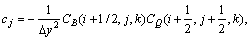
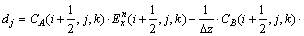
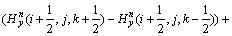
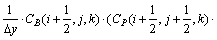
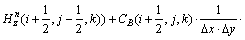
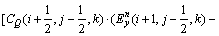
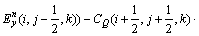
(4)
则式(3)可改写为：
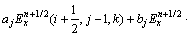
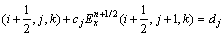(5)
显然，式(5)可写为矩阵形式：
AX=Y (6)
其中：
； 
；
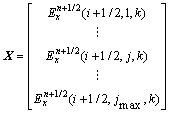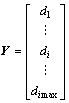矩阵A为三对角条带矩阵，通过追赶法可求解。其首、末元素b1，c1及ajmax和bjmax需要用吸收边界条件得到。显然，实际执行第一过程时，用类似的方法可解出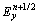
，
，
，
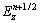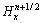和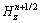。当实际执行n+1/2→n+1过程时，用类似的方法可解出
，
，
，
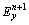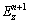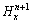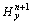和
。
2 单轴各向异性完全匹配层边界条件
在GPR三维正演模拟中，吸收边界条件起着重要作用，它直接影响到FDTD计算的精确度。考虑到引入到本文的边界条件必须与ADI-FDTD差分格式相匹配，而不破坏时间步进的无条件稳定性原则[15]。具有宽频带吸收特性的PML边界条件是目前最合适的吸收边界条件，它主要有以下几种形式：基于分裂场的Berenger PML[16]、非分裂场的CPML[17]和UPML[18]等。CPML吸收层则对低频分析有一定的优越性；Berenger PML的理论体系是非Maxwell方程的物理机制模糊，同时，其电磁场分量分裂技术增加了数值实现的难度和计算机内存的占用；而UPML不需要对电场和磁场进行分裂，节约计算机存储量，提高了计算精度和计算效率，迭代公式简单，便于编程。基于它的诸多优点，本文选用UPML边界条件并结合ADI-FDTD方法进行探地雷达数值模拟。
由电磁场与电磁波的理论可知：在UPML媒质的角形区域中，三维GPR波的UPML有6个平面区、12个棱边区和8个角顶区，Maxwell方程可以表示为：
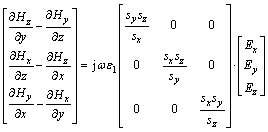(7)
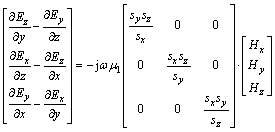(8)
式中：UPML参数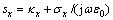
；sy=κy+ 
；
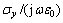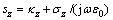；sx，sy和sz为单轴各向异性介质分别在x，y和z方向对角张量；参数κx，κy和κz是为了有效吸收到达UPML层而设置的误差函数。用来吸收到达UPML层的凋落波；参数σx和σy为UPML层中人为设置的电导率函数。为了便于得到时间推进式，引入中间变量D和B，令
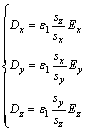(9)
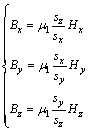(10)
将参数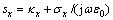，sy=κy+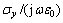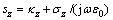，分别代入式(9)和(10)中，以Dx和Bx为例可得到：
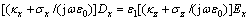(11)
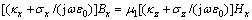(12)
整理式(11)和(12)，并应用频域到时域算子关系
，将式(11)和(12)变为时域形式为：
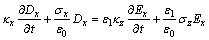(13)
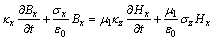(14)
Dy，Dz，By和Bz分量公式可通过类似的方式得到：
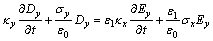
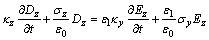
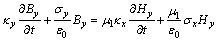
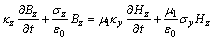
则式(7)与(8)变为：
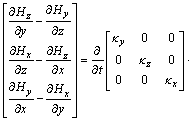
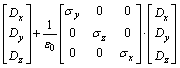(15)
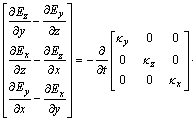
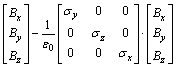(16)
式(15)中的3个方程构成了H→D的时间推进计算式，式(13)中Dx及其类似推得的Dy和Dz的3个方程构成了D→E的时间推进计算式，它们一起构成了H→D→E的时间推进公式；式(16)中的3个方程构成了E→B的时间推进计算式，式(14)中Bx及其类似推得的By和Bz的3个方程构成了B→H的时间推进计算式，它们一起构成了UPML边界条件的E→B→H的时间推进公式。这样，这12个一阶偏微分一起构成了UPML边界条件的整个时间推进计算公式。下面给出三维GPR数值模拟的UPML边界条件的ADI-FDTD形式。为了公式形式简明，设
(17)
在子时间步n→n+1/2步中，对偏微分方程左边的第1个方向导数?Hz/?y的差分离散取显式，对第2个方向导数?Hy/?z的差分离散取隐式。于是，式(15)中左边第1项的ADI-FDTD离散式为
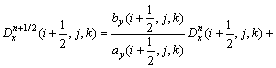
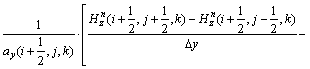
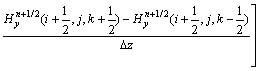(18)
式(15)和(16)的其他分量差分方程可采用类似的方法得到。显然，在执行n→n+1/2 UPML差分计算时，同样遇到等式右端与左端同时间步的场分量，导致无法进行时间步推进，可用上文中类似算法进行求解。其他的场分量及其n+1/2→n+1过程也可类似得到。
为验证UPML边界条件的吸收效果，在三维空间中加入1个Ricker子波，模拟它在有、无UPML边界条件下雷达波传播的空间特征。在无边界条件下，三维Ex分量波场如图1(a)所示，可见：截断边界的4条边上波的反射非常明显，4个角点引起的虚假反射尤其明显。图1(b)所示为UPML边界条件下的三维Ex分量波场，计算区域中的等值线是非常规则的同心圆，4个边角没有明显的反射，表明UPML层的吸收效果很好，雷达波无反射地进入完全匹配层后迅速被衰减，验证了该方法作为雷达正演的吸收边界是非常有效。
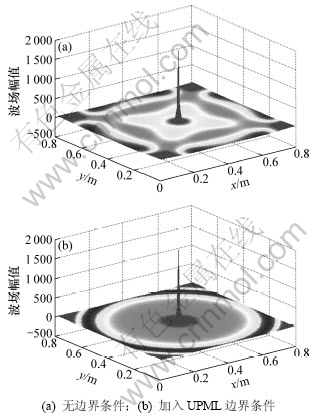
图1 有、无UPML边界条件的Ex分量波场快照对比图
Fig.1 Ex wave field snapshot map with or without adding UPML boundary condition
3 GPR三维全波场数值模拟实例
设模拟空间是x，y和z方向长度分别为0.60，1.30和0.65 m组成的区域，区域上部为空气层，厚度为0.10 m，下部为混凝土，其介电常数为6.0，电导率为0.001 S/m。在此混凝土中介质中，由x×y×z=(0.15~0.45) m×(0.45~0.85) m×(0.25~0.50) m构成的长方体空洞，空洞内的x×y×z=(0.26~0.34) m×(0.61~0.69) m×(0.42~0.50) m的位置上存在1个立方体混凝土，该复杂的三维模型示意图如图2所示。应用基于三维UPML边界条件的ADI-FDTD方法对该模型进行数值模拟。模拟过程中ricker子波的主频为600 MHz，脉冲位置位于地表，测线平行于y轴，共布置了27条测线。设第1条雷达测线的位置位于x=0.025 m处，测线间距为0.02 m，最后1条测线位于x=0.565 m处，每条测线共采集40道数据，为得到好的雷达正演数据，检测过程中采用发射天线与接收天线分离的方式，第1个脉冲点位为y=0.125，第1个接收点位为y=0.375。网格空间步长为0.01 m，UPML边界网格厚度设为8层，时窗长度为12×10-9 s，约为623个时间步长。受CFL条件的影响，应用常规的FDTD正演软件如GPRmax，Author：Antonis Giannopoulos取时间步长为1.925 833 3×10-11 s，在Intel(R)Core?2 Quad CPU，Q8200@2.33GHz，3.25GB的内存物理地址扩展，Window XP操作系统的HP Pavilion Elite m9655cn高性能台式机上计算该雷达剖面40道数据，需时17 min 13 s，而本文应用结合UPML边界条件的ADI-FDTD算法采用的时间步长为2.5×10-11 s，采用更大时间步长的同时保证了算法的稳定性，尽管还需求解大型线性方程组，但本文方法把计算时间缩短了4 min 23 s，效率提高了近1/4。图3(a)所示为空洞模型的雷达3D立体剖视图；图3(b)所示为空洞模型的雷达x方向与z方向切片图；图3(c)所示为空洞模型的雷达z向雷达波场振幅切片图。从图3可见立方体空洞与小立方体混凝土的雷达波场反射。图3(b)~3(c)中圆状白色高亮显示的位置，准确地指示了小立方体混凝土的位置。
为了更全面地了解雷达波在三维空间的传播特性，在图2所示模拟区域的0.300 m×0.650 m×0.325 m位置加入Richer子波，采用自激自收的方式，并在x=0.3 m的位置对雷达波场进行快照。文中选取了6个雷达波电、磁场分量在150，200和250个时间步所得的全波场快照，具体传播特征如图4所示。分析图4(a)中电场Ex分量可知：雷达波以均匀球面波幅射方式迅速向外扩散传播，在150个时间步开始由混凝土介质进入上层的空气介质中，由于雷达波在空气介质中传播速度较混凝土传播速度快，导致在200~250个时间步中，出现不同的双曲线弧形。分析图4所示的电场Ey分量可知在不同时间步的波场快照中，长方体空洞与小立方体混凝土的空间位置与大小。而在图4中电场Ez分量的不同时间步的波场快照中，0.15 m处的空气与混凝土分界面在图中非常清晰。再分析图4中3个磁场分场Hx，Hy和Hz的波场快照，雷达波也以源为中心迅速向外扩散，近似地以垂直方向呈轴对称分布。分析各磁场分量可知，磁场分量的波场快照对于异常体特征的反映没有电场分量明显，尽管在个别磁场分量的特定时刻，异常体的特征也可得到体现，但是，总体来说，磁场分量的波场快照更加复杂，里面蕴含了更加丰富的雷达波场信息和规律，需要进行更深入的研究和总结。
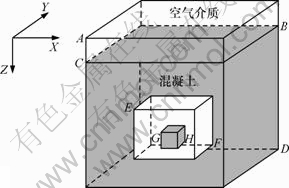
图2 三维模型示意图
Fig.2 Sketch map of 3D model
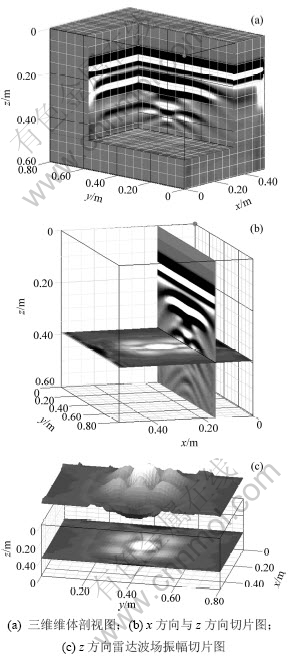
图3 三维雷达模型正演模拟剖视图与切片图
Fig.3 GPR fence diagram and slice map of 3D forward simulation
图4 三维空间雷达模型全波场快照
Fig.4 GPR wave propagation snapshots of full wave in 3D space
4 结论
(1) 结合交替方向隐式差分的特点，从Maxwell方程组出发，推导了三维雷达波ADI-FDTD方法的迭代计算公式，并分别给出了详细的计算步骤，得到了最终需求解的三对角条带矩阵，并指出可通过高斯消元方法求得其解。
(2) 将UPML吸收边界引入到GPR数值模拟的ADI-FDTD方法中，而不破坏ADI-FDTD方法的无条件稳定性，消除了截断边界处的强反射，为探地雷达的正演模拟提供了一种新的模拟手段。尽管ADI-FDTD方法是一种无条件稳定的交替方向隐式时域有限差分法，它克服了常规FDTD法受CFL约束条件的限制，但是，需要迭代求解大型线性方程组。
(3) 设计了三维空间的复杂地电模型，应用基于UPML边界条件的ADI-FDTD算法并编制了相应的计算程序，对该复杂模型进行了数值模拟，得到了不同时刻的雷达全波场快照和剖视图、切片图，通过分析这些图件，可对于雷达波在三维空间的传播特征有了更系统的了解和更清楚的认识，有助于指导雷达资料的解释。
参考文献：
[1] 底青云, 王妙月. 雷达波有限元仿真模拟[J]. 地球物理学报,1999, 42(6): 818-825.
DI Qing-yun, WANG Miao-yue. 2D finite element modeling for radar wave[J]. Chinese J Geophys, 1999, 42(6): 818-825.
[2] LIU Qing-huo, FAN Guo-xin. Simulations of GPR in dispersive media using a frequency-dependent PSTD algorithm[J]. IEEE Geosci Remote Sensing, 1999, 37(5): 2317-2324.
[3] 刘四新, 曾昭发, 徐波. 三维频散介质中地质雷达信号的FDTD数值模拟[J]. 吉林大学学报: 地球科学版, 2006, 36(1): 123-127.
LIU Si-xin, ZENG Zhao-fa, XU Bo. FDTD simulation for Ground Penetrating Radar signal in 3-Dimensional dispersive medium[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(1): 123-127.
[4] 肖明顺, 昌彦君, 曹中林, 等. 探地雷达数值模拟的吸收边界条件研究[J]. 工程地球物理学报: 地球科学版, 2008, 5(3): 315-320.
XIAO Ming-shun, CHANG Yan-jun, CAO Zhong-lin, et al. Research on boundary conditions in forward modeling of Ground Penetrating Radar[J]. Chinese Journal of Engineering Geophysics, 2008, 5(3): 315-320.
[5] 李静, 曾昭发, 吴丰收, 等. 探地雷达三维高阶时域有限差分模拟研究[J]. 地球物理学报, 2010, 53(4): 974-981.
LI Jing, ZENG Zhao-fa, WU Feng-shou, et al. Study of three dimension high-order FDTD simulation for GPR[J]. Chinese J Geophys, 2010, 53(4): 974-981.
[6] Szerbiak R B, McMechan G A, Corbeanu R, et al. 3-D characterization of a clastic reservoir analog: From 3-D GPR data to a 3-D fluid permeability model[J]. Geophysics, 2001, 66(4): 1026-1037.
[7] 郑奎松. FDTD网络并行计算及ADI-FDTD方法研究[D]. 西安: 西安电子科技大学理学院, 2005: 10-20.
ZHENG Kui-song. Study of FDTD parallel computing and ADI-FDTD method[D]. Xi’an: Xidian University. Institute of Science, 2005: 10-20.
[8] Krumpholz M, Katehi L P B. MRTD: New time-domain schemes based on multiresolution analysis[J]. IEEE Trans Microwave and Guided Wave Letters, 1996, 44(4), 555-571.
[9] LIU Qing-huo. The PSTD algorithm: a time-domain method requiring only two cells per wavelength[J]. Micro Opt Technol Lett, 1997, 10(6): 158-165.
[10] FU Wei-ming, TAN Eng-leong. Stability and dispersion analysis for higher order 3-D ADI-FDTD method[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(11): 3691-3696.
[11] Krumpholz M, Winful H G, Katehi L P B. Nonlinear time-domain modeling by multiresolution time domain(MRTD)[J]. IEEE Trans on MTT, 1997, 45(3): 385-393.
[12] LIU Qing-liang, CHEN Yin-chao. Application of the PSTD for scattering analysis[J]. IEEE Transactions on Antennas and Propagation, 2002, 50(9): 1317-1319.
[13] Namiki T. 3-D ADI-FDTD method-unconditionally stable time-domain algorithm for solving full vector Maxwell’s equations[J]. IEEE Transactions on Microwave Theory and Techniques, 2000, 48(10): 1743-1748.
[14] 葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 2版. 西安: 西安电子科技大学出版社, 2005: 25-60.
GE De-biao, YAN Yu-bo. Fintie-difference time-domain method for electromagnetic waves[M]. 2nd ed. Xi’an: Xidian University Press, 2005: 25-60.
[15] Gedney S D, LIU Gang, Roden J A. Perfectly matched layer media with CFS for an unconditionally stable ADI-FDTD method[J]. IEEE Transactions on Antennas and Propagation, 2001, 49(11): 1554-1559.
[16] Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200.
[17] Roden J A, Gedney S D. Convolutional PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334-339.
[18] LIU Gang, Gedney S D. Perfectly matched layer medium for an unconditionally stable three-dimensional ADI-FDTD method[J]. IEEE Microwave and Guided Wave Letters, 2000, 10(7): 261-263.
(编辑 陈灿华)
收稿日期：2010-11-15；修回日期：2011-01-20
基金项目：国家自然科学基金资助项目(40804027，41074085)；湖南省自然基金重点项目(09JJ3084)；教育部博士点新教师专项科研基金资助项目(200805331082)
通信作者：冯德山(1978-)，男，湖南祁阳人，博士，副教授，从事探地雷达与地震勘探的研究；电话：0731-88836145(O)；E-mail：fengdeshan@126.com
